高斯白噪声激励下分数阶Duffing-Van der Pol系统的稳态响应∗

马颜颜 宁丽娟

（陕西师范大学数学与信息科学学院，西安 710119）

高斯白噪声激励下分数阶Duffing-Van der Pol系统的稳态响应∗

马颜颜 宁丽娟†

（陕西师范大学数学与信息科学学院，西安 710119）

应用随机平均法研究了高斯白噪声激励下含有分数阶阻尼项的Duffing-Van der Pol系统的稳态响应.首先应用基于广义谐和函数的随机平均法得到系统关于幅值的平均伊藤微分方程并建立相应的平稳FPK方程，求解该平稳FPK方程的近似理论解得到系统幅值的稳态概率密度.分析幅值、位移和速度的稳态概率密度探究分数阶阻尼项以及其它参数对系统稳态响应的影响.发现降低分数阶的阶数可以增强系统的响应而增大分数阶的系数可以减弱系统响应.最后对原系统进行Monte Carlo数值模拟验证近似理论解的有效性.

响应， 分数阶， Duffing-Van der Pol， 高斯白噪声， 随机平均法， Monte Carlo模拟

引言

Einstein在1905年首次提出了随机激励下的强非线性系统.它可以广泛地应用于力学、控制、生物、航天科学、金融、社会科学以及粘弹性材料等众多领域中［1-5］.非线性系统自被提出以来一直都是非常具有吸引力和发展前景的研究领域.然而随着深入的研究，人们发现许多实际系统中存在记忆因子而不能用传统的整数阶模型进行模拟［6，7］.为解决这个问题Bagley和Torvik在文献［8，9］中证明了分数阶导数模型能够更好地模拟粘弹性材料.另外越来越多的研究［10-14］表明含有分数阶导数的非线性系统比传统的整数阶系统能更精确地模拟实际物理系统的内部性质且给出更合理的解释.

事实上，近年来研究者们已应用多种方法研究了在不同噪声激励下的分数阶非线性系统的动力学行为，取得了丰硕的成果:文献［15］应用广义谐波技术和能量包线随机平均法研究了在高斯白噪声激励下含有分数阶的Duffing振子的稳态响应.文献［16］讨论了高斯白噪声激励下含有Caputo型分数阶阻尼的非线性碰撞振动系统的随机分岔.该文献主要应用了Zhuravlev非光滑变换和随机平均法.文献［17］利用随机平均法探究了分数阶Duffing振子在谐和力和白噪声共同激励下的随机跳跃和随机分岔.应用随机平均法文献［18］讨论了分数阶单自由度非线性系统在高斯白噪声激励下的响应和稳态.在文献［19］中应用随机平均法研究了一系列含有Caputo型分数阶导数的自激系统在高斯白噪声激励下的随机响应.文献［20］研究了实噪声激励下含有分数阶阻尼项的多自由度非线性振子的首次穿越损坏.上述的研究基本上是应用标准随机平均法或者能量包线随机平均法.可以看到随机平均法不仅可以简化运动方程还可以降低方程的维数，因此经常被用来求解含有分数阶导数的非线性系统的近似理论解.

除了随机平均法还有许多其它有效的方法来求解分数阶非线性系统的理论解.比如文献［21］应用摄动法分析了含有分数阶阻尼项的拟线性系统在泊松白噪声激励下的响应.文献［22，23］应用L-P方法和多尺度方法研究含有分数阶阻尼项的Duffing振子的动力学响应.频域方法被应用于研究分数阶随机系统［24］.在文献［25］中提出用特征向量展开方法和拉普拉斯变换方法研究含有分数阶阻尼的随机动力学系统.

Duffing-Van der Pol系统是非常具有代表性的强非线性模型而且被广泛应用于科学、生物、工程等很多领域.在文献［26］中用随机双Duffing-Van der Pol网络模型模拟了脑电图信号的输出.前面的文献中涉及到多种噪声，其中高斯白噪可用具体数学表达式表述，便于推导分析和运算.在这篇文章中应用随机平均法研究高斯白噪声激励下分数阶Duffing-Van der Pol系统的稳态响应.

文章结构如下:第1节介绍分数阶Duffing-Van der Pol系统模型和Riemann-Liouvile型分数阶导数的定义.第2节应用随机平均法求得原系统幅值的平均伊藤微分方程并建立相应的FPK方程，求解FPK方程得到幅值的稳态概率密度.第3节通过稳态概率密度分析参数变化对系统稳态响应的影响，并对原系统进行Monte Carlo数值模拟检验理论结果的有效性.第4节给出文章结论.

1 系统模型

考虑如下高斯白噪声激励下含有分数阶导数的Duffing-Van der Pol系统:

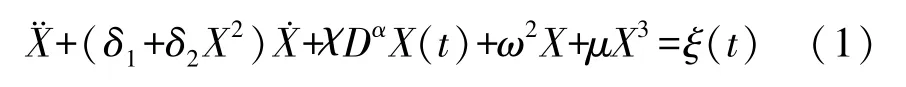
这里δ1表示线性阻尼的系数；δ2为非线性阻尼的系数；ω无阻尼系统的自然频率；μ为非线性的强度；g（X）＝ω2X+μX3代表回复力是强非线性函数；分数阶导数DαX（t）采用Riemann-Liouville定义:

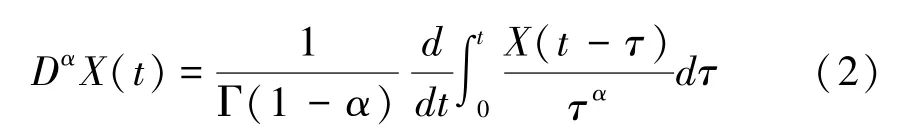
这里 α（0＜α＜1）是分数阶的阶数，Γ（·）是伽马函数，χ表示分数阶导数项的系数．ξ（t）为高斯白噪声，均值和方差分别为:

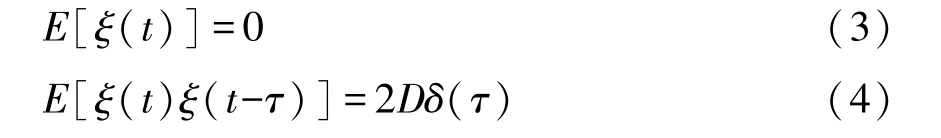
其中δ（τ）是狄拉克函数．

2 随机平均法和近似解

根据广义谐和函数系统（1）在原点附近的运动可以近似为周期的，因此有如下变换［27］:

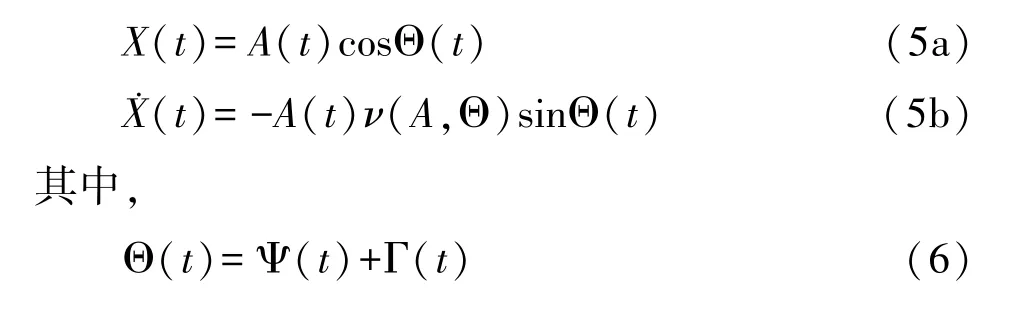
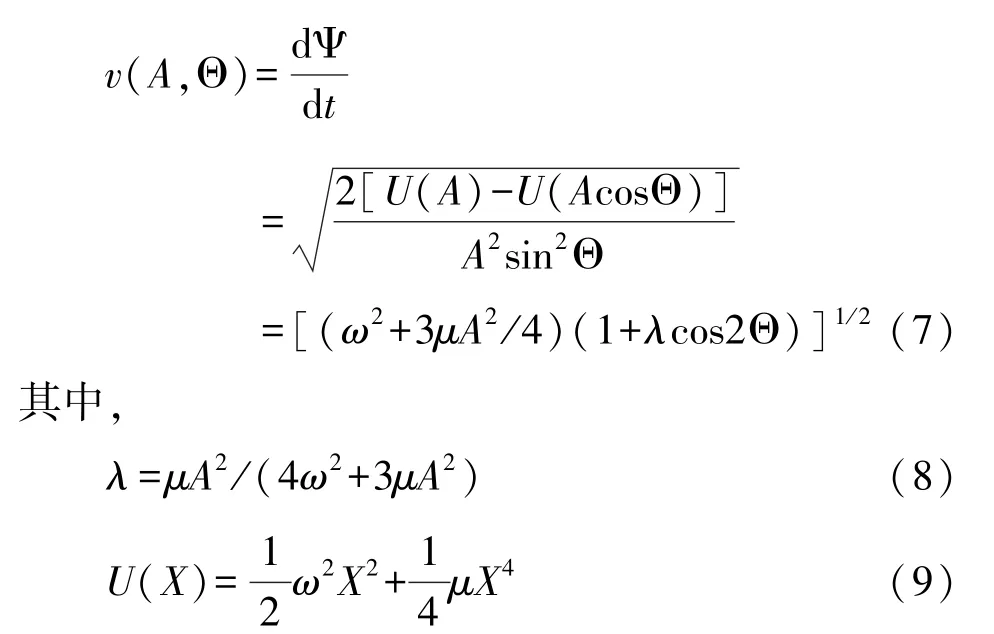
这里 U（X）是势函数；cosΘ（t）和 sinΘ（t）表示广义谐和函数；ν（A，Θ）和 Θ（t）分别表示系统的瞬时频率和瞬时相位．

现把ν（A，Θ）展开成傅立叶级数的形式如下:

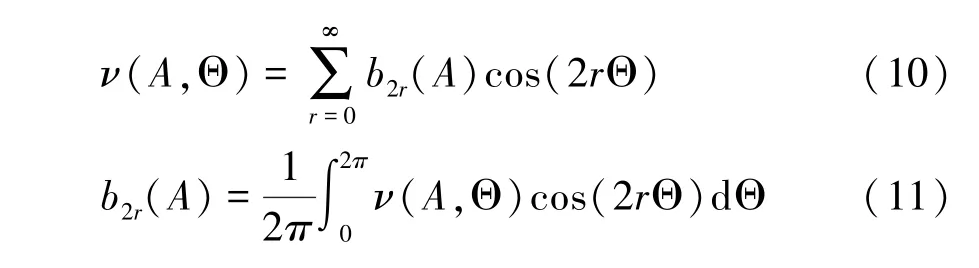
方程（10）关于 Θ 在［0，2π］上积分得到近似平均频率，即:

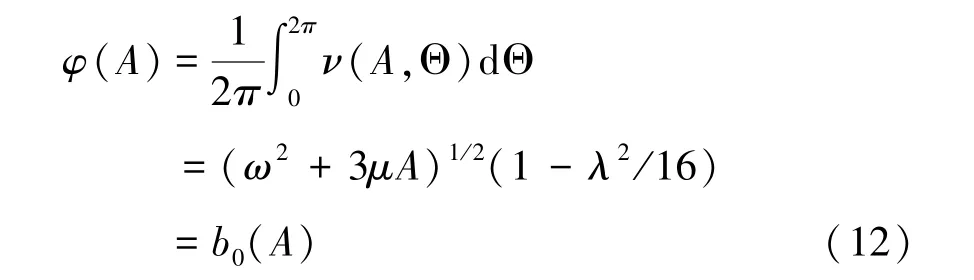
把方程（12）代入方程（6）可得到 Θ（t）的近似表达式:

由于A（t）和 Γ（t）是关于时间 t的慢变过程，所以可由方程（13）得到如下近似表达式:

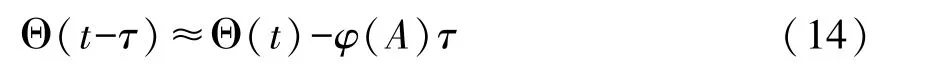
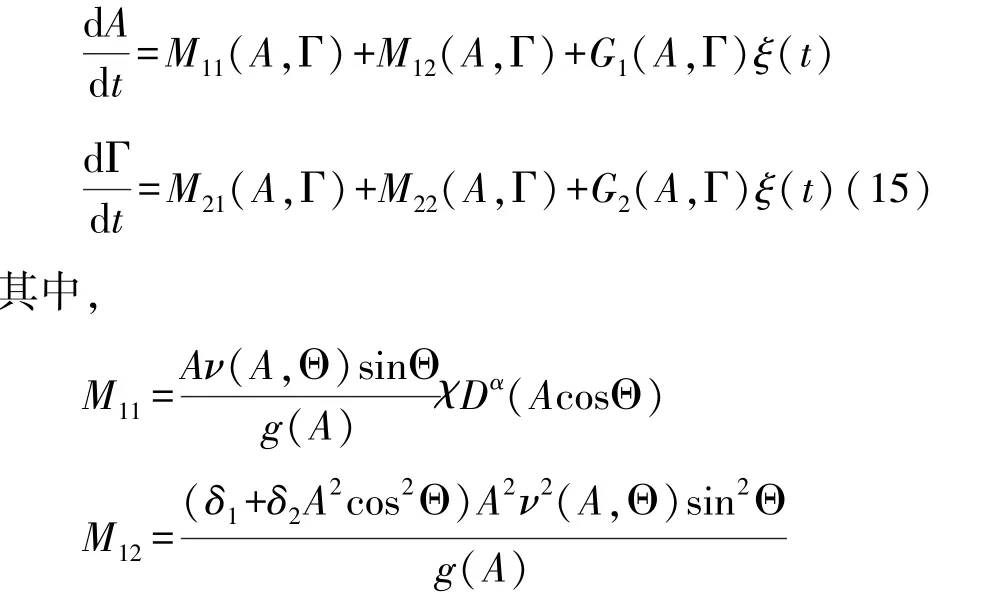
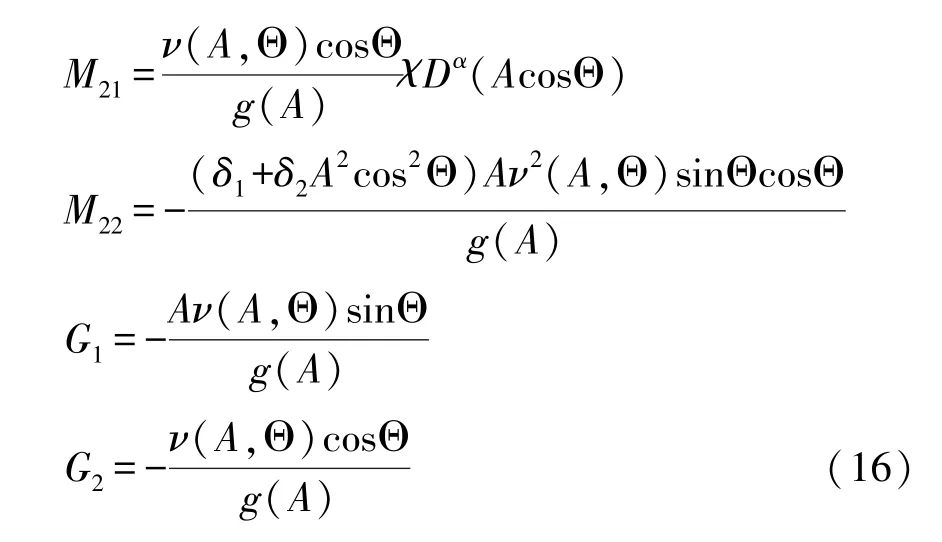
由方程（15）可得到 Stratonovich随机微分方程，加上 Wong-Zakai［28］修正项并平均后可得对应的伊藤平均微分方程:

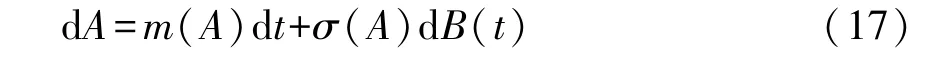
其中漂移项和扩散项分别为:

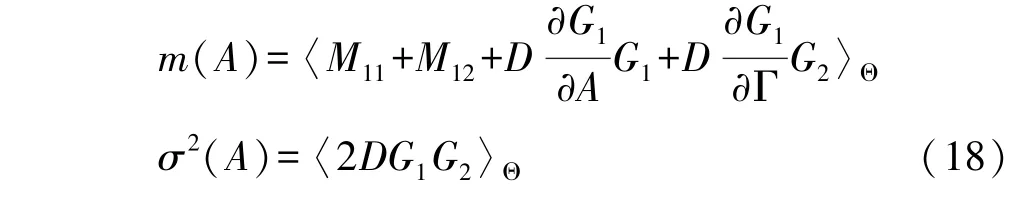
这里〈·〉Θ是关于 Θ 在［0，2π］上的平均．

考虑近似关系式（14），含有分数阶导数项的〈M11〉Θ可进一步化简为:

这里FPK方程关于A的边界条件为当A＝0时 p＝finite以及当 A→∞时 p、∂p／∂A→0．依据这些边界条件求解FPK方程（24）得到原系统（1）幅值的稳态概率密度:

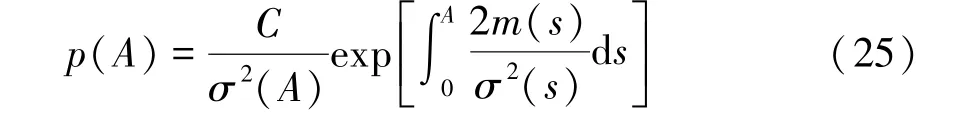
其中C 表示归一化常数，m（s）和 σ2（s）的表达式由（22）式和（23）式给出．

总能H的稳态概率密度为:

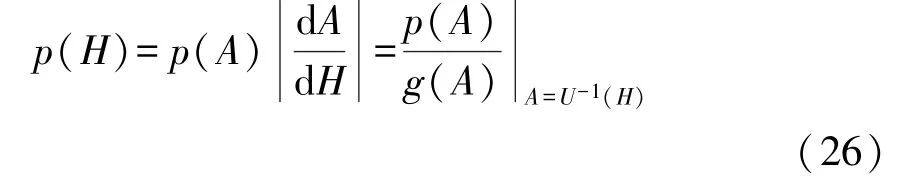
A＝U-1（H）表示 H＝U（A）的反函数；H 表示系统的总能．

广义位移X和速度˙X的联合稳态概率密度为:

3 稳态响应和参数分析

分析系统参数和噪声强度的变化对系统稳态响应的影响，并对原系统进行Monte Carlo数值模拟验证理论方法的有效性［29，30］．图 1 给出了幅值A、位移X和速度˙X（Y＝˙X）的稳态概率密度曲线．其中实线表示理论结果，圆点表示原系统的Monte Carlo数值模拟结果．参数取值如下:α＝0．7，χ＝4，ω＝2，μ＝1．6， D＝0．06，δ1＝ 0．05，δ2＝-0．05．由图 1知近似解析解与原系统的Monte Carlo数值模拟结果相吻合．这表明随机平均法可以有效地求解高斯白噪声激励下分数阶Duffing-Van der Pol系统的稳态响应．

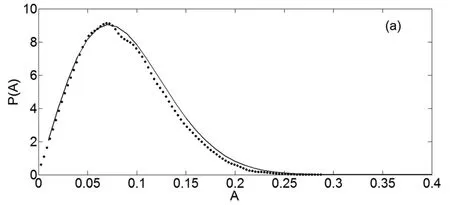
图1（a） 幅值A的稳态概率密度曲线Fig.1（a） Stationary probability density of amplitude A

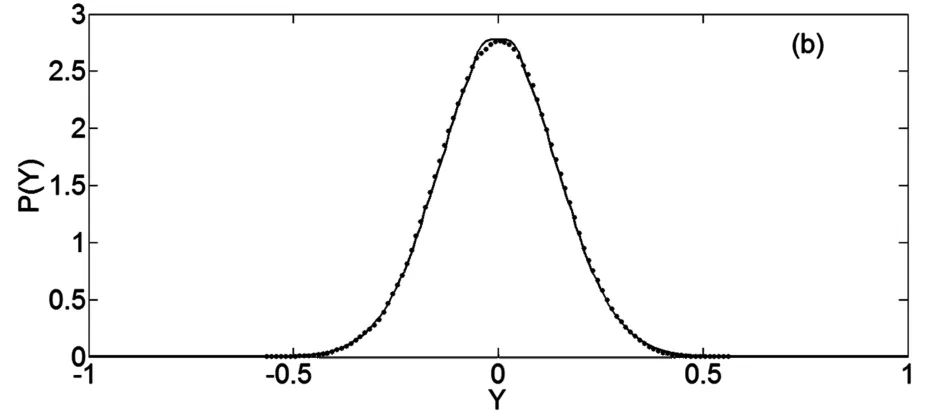
图1（b） 速度Y的稳态概率密度曲线Fig.1（b） Stationary probability density of velocity Y

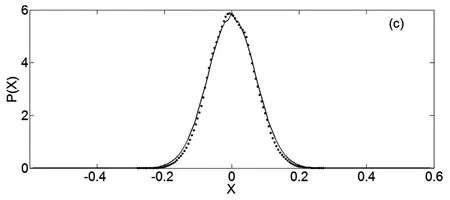
图1（c） 位移X的稳态概率密度曲线Fig.1（c） Stationary probability density of displacement X

图2给出了对于不同分数阶α的幅值A的稳态概率密度曲线．参数取值如下:χ＝3，ω＝2，μ＝1．5，D＝0．06，δ1＝0．05，δ2＝ -0．05．其中实线表示理论结果，圆点表示原系统的Monte Carlo数值模拟结果．图2显示随着α增大，曲线的峰值也逐渐增大，峰值的位置逐渐向左移．稳态概率密度曲线的峰值越高，表示峰值处的概率越大，即分数阶的阶数α越大，系统在小振幅处取值的概率就越大．由此可以得出增大α可以减弱系统的稳态响应．这个结论也可由图3得到证实．由图3可看出α增大时，位移的时间历程图变窄，反应系统的稳态响应随着α增大而减弱．另一方面我们也可以由广义速度和位移的稳态联合概率密度来分析α对系统稳态响应的影响．图4给出了不同分数阶α的稳态联合概率密度．可以看到随着α的增大，图像由粗矮状逐渐变细、增高．这表示增大α时，系统的响应逐渐减弱．这里指出图3和图4中的参数取值和图2中的参数取值是一样的．

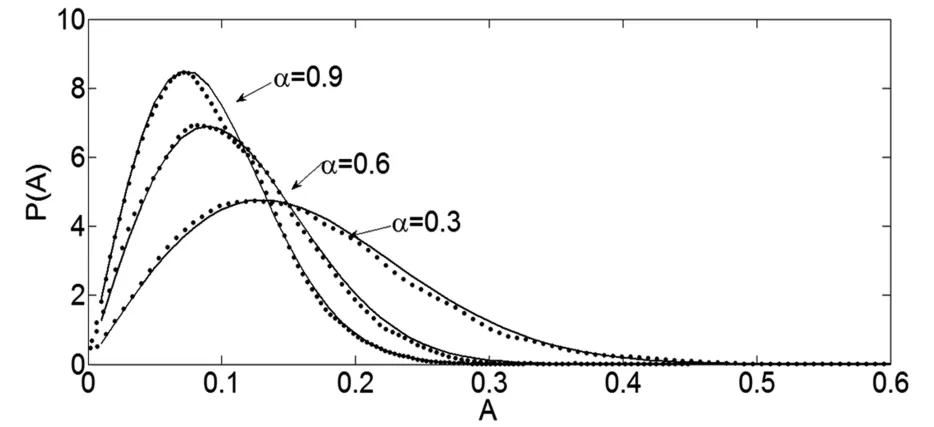
图2 对于不同分数阶数α幅值A的稳态概率密度曲线Fig.2 Stationary probability density of amplitude A with different fractional order α

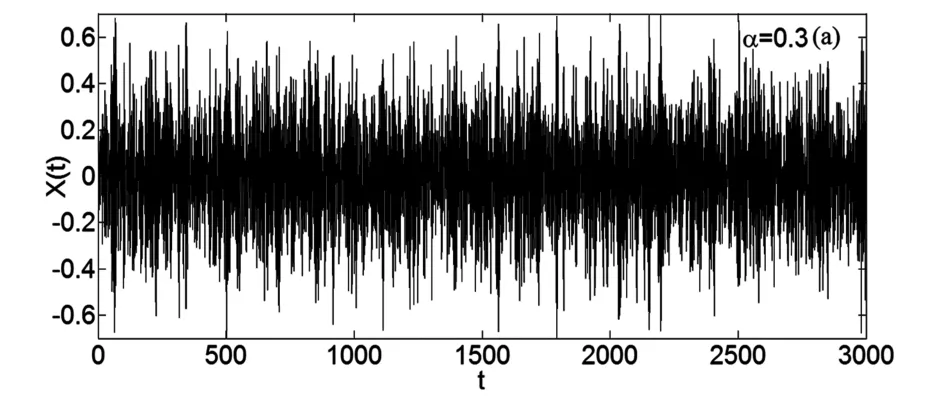
图3（a） 对于不同分数阶数α位移X的时间历程图Fig.3（a） Time history of the displacement X with different fractional order α

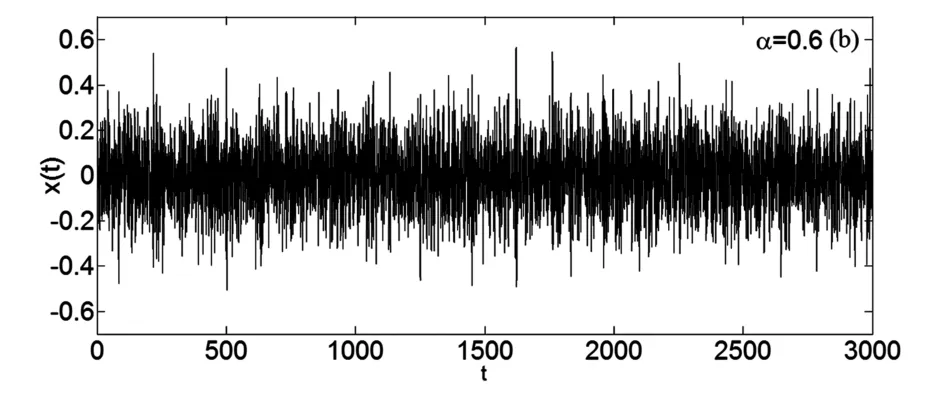
图3（b） 对于不同分数阶数α位移X的时间历程图Fig.3（b） Time history of the displacement X with different fractional order α

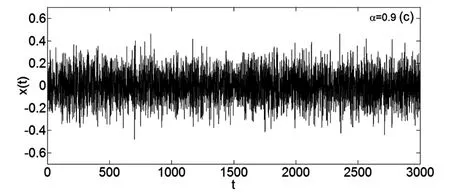
图3（c） 对于不同分数阶数α位移X的时间历程图Fig.3（c） Time history of the displacement X with different fractional order α

图5给出对于不同分数阶系数χ的幅值稳态概率密度曲线．参数取值如下:α＝0．9，ω＝0．8，μ＝4，D＝0．04，δ1＝0．05，δ2＝ -0．05．其中实线表示理论结果，圆点表示原系统的Monte Carlo数值模拟结果．观察图5可以看出随着χ的增大，概率密度曲线的峰值增大并且峰值的位置逐渐左移，由此分析得到增大χ同样可以减弱系统的稳态响应．

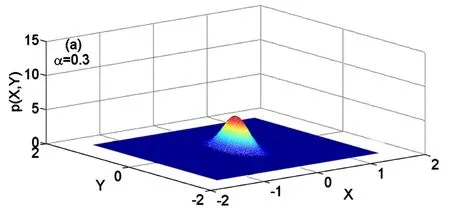
图4（a） 关于广义位移X和速度Y的稳态联合概率密度Fig.4（a） Joint stationary probability density of the generalized displacement X and velocity Y

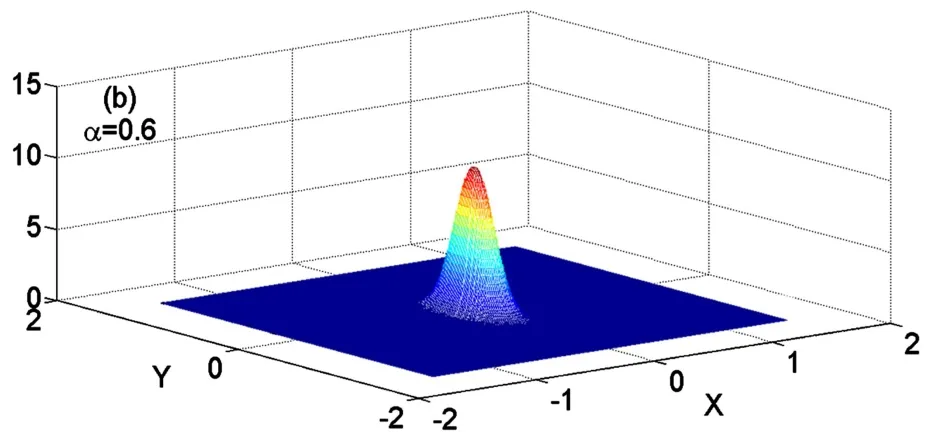
图4（b） 关于广义位移X和速度Y的稳态联合概率密度Fig.4（b） Joint stationary probability density of the generalized displacement X and velocity Y

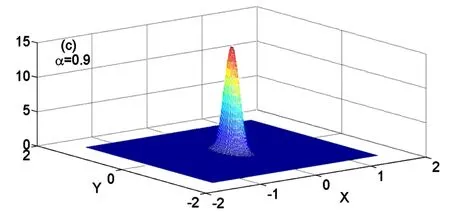
图4（c） 关于广义位移X和速度Y的稳态联合概率密度Fig.4（c） Joint stationary probability density of the generalized displacement X and velocity Y

在实际系统中噪声对系统的影响是不可忽视的．图6给出了不同噪声强度D影响下幅值的稳态概率密度曲线．实线表示理论结果，圆点表示原系统的Monte Carlo数值模拟结果．参数取值如下:α＝0．6，ω＝2，μ＝1．2，χ＝2，δ1＝0．05，δ2＝-0．05．观察图6可以看出增大噪声强度D幅值A的稳态概率密度曲线的峰值逐渐减小，并且峰值的位置逐渐向右移．说明增大D能够增强系统的稳态响应．

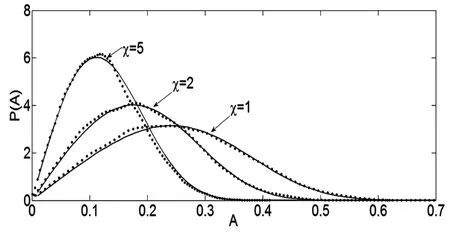
图5 对于不同分数阶系数χ幅值A的稳态概率密度曲线Fig.5 Stationary probability density of the amplitude A with different fractional derivative intensitiesχ

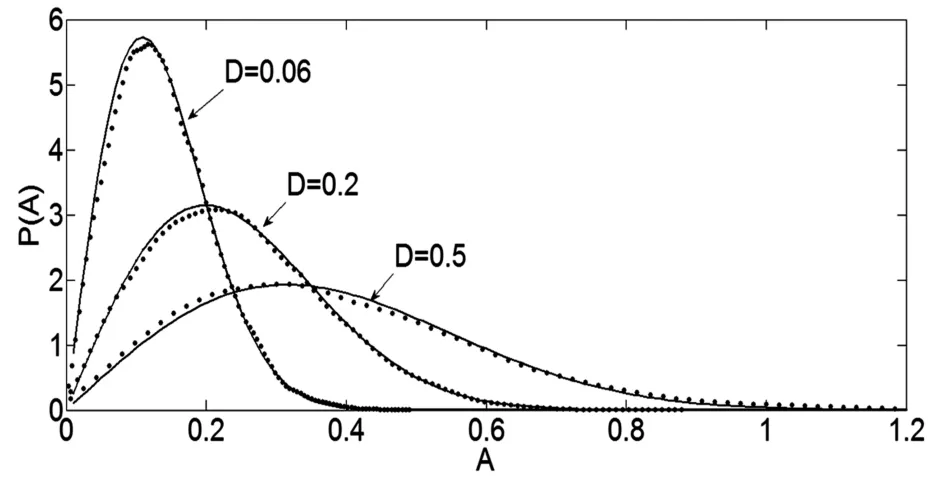
图6 对于不同噪声强度D幅值A的稳态概率密度曲线Fig.6 Stationary probability density of the amplitude A with different random intensities D

最后图7给出了不同自然频率ω影响下的稳态概率密度．参数取值如下:α＝0．6，μ＝1．5，χ＝1．2，D＝0．06，δ1＝0．05，δ2＝-0．05．实线表示理论结果，圆点表示原系统的Monte Carlo数值模拟结果．从图7中分析得增大ω可以减弱系统的稳态响应．

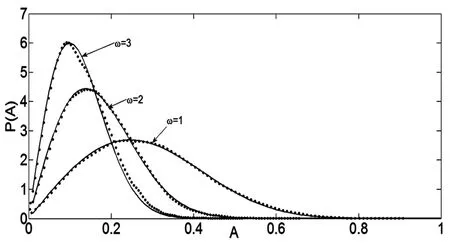
图7 对于不同自然频率ω幅值A的稳态概率密度曲线Fig.7 Stationary probability density of the amplitude A with different natural frequency ω

4 结论

本文研究了高斯白噪声激励下分数阶Duffing-Van der Pol系统的稳态响应.应用广义谐和函数和随机平均法将原系统转化为关于幅值的平均伊藤微分方程，进而建立相应的PFK方程，并求解得到幅值的稳态概率密度的近似解析解.对原系统进行Monte Carlo数值模拟验证了理论结果的有效性.分析结果得出:增大分数阶阶数α、分数阶系数χ以及自然频率ω都能明显地减弱系统的稳态响应．相反地，增大高斯白噪声的强度D可以增强系统的稳态响应.

1 Wu W F，Lin Y K.Cumulant-neglect closure for non-linear oscillators under random parametric and external excitations.InternationalJournalofNon-LinearMechanics，1984，19（4）:349～362

2 Zeng Y，Zhu W Q.Stochastic averaging of n-dimensional non-linear dynamical systems subject to non-Gaussian wideband random excitations.International Journal of Non-Linear Mechanics， 2010，45（5）:572～586

3 Zhu W Q，Cai G Q.Random vibration of viscoelastic system under broad-band excitations.International Journal of Non-Linear Mechanics， 2011，46（5）:720～726

4 Ling Q，Jin X L，Huang Z L.Response and stability of SDOF viscoelastic system under wideband noise excitations.Journal of the Franklin Institute， 2011，348（8）:2026 ～2043

5 李东武，徐超.基于时频域交替法的迟滞非线性振动系统的稳态响应分析.动力学与控制学报，2016，14（3）:217～222 （Li D W， Xu C.Alternating time／frequency domain method for calculating the steady-state response of hysteresis nonlinear vibration systems.Journal of Dynamics and Control， 2016，14（3）:217～222 （in Chinese））

6 Mainardi F.Fractional calculus and waves in linear viscoelasticity:an introduction to mathematical models.Imperial College Press，2010:368

7 Alvelid M，Enelund M.Modelling of constrained thin rubber layer with emphasis on damping.Journal of Sound and Vibration， 2007，300（3-5）:662～675

8 Bagley R L， Torvik P J.Fractional calculus—A different approach to the analysis of viscoelastically damped structures.Aiaa Journal， 2012，21（5）:741～748

9 Bagley R L，Torvik P J.Fractional calculus in the transient analysis of viscoelastically damped structures.Aiaa Journal， 1985，23（6）:918～925

10 Machado J A T.And I say to myself:What a fractional world！.Fractional Calculus and Applied Analysis， 2011，14（4）:635～654

11 Machado J A T.Fractional order modelling of fractionalorder holds.Nonlinear Dynamics， 2012，70（1）:789～796

12 Machado J A T.Fractional Calculus:Application in modeling and control.Springer New York， 2013:279～295

13 Machado J A T，Costa A C，Quelhas M D.Fractional dynamics in DNA.Communications in Nonlinear Science and Numerical Simulation， 2011，16（8）:2963～2969

14 Mainardi F.Fractional relaxation-oscillation and fractional diffusion-wave phenomena.Chaos Solitons and Fractals，1996，7（9）:1461～1477

15 Chen L C，Wang W H，Li Z S，et al.Stationary response of Duffing oscillator with hardening stiffness and fractional derivative.International Journal of Non-Linear Mechanics，2013，48:44～50

16 Yang Y G，Xu W，Sun Y H，et al.Stochastic bifurcations in the nonlinear vibroimpact system with fractional derivative under random excitation.Communications in Nonlinear Science and Numerical Simulation， 2017，42:62～72

17 Chen L C，Zhu W Q.Stochastic jump and bifurcation of Duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations.International Journal of Non-Linear Mechanics， 2011，46（10）:1324～1329

18 Huang Z L，Jin X L.Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative.Journal of Sound Vibration， 2009，319（3）:1121～1135

19 Yang Y G，Xu W，Gu X D，et al.Stochastic response of a class of self-excited systems with Caputo-type fractional derivative driven by Gaussian white noise.Chaos，Solitons and Fractals， 2015，77:190～204

20 Chen L C，Zhu W Q.First passage failure of SDOF nonlinear oscillator with lightly fractional derivative damping under real noise excitations.Probabilistic Engineering Mechanics， 2011，26（2）:208～214

21 Yang Y G，Xu W，Yang G D，et al.Response analysis of a class of quasi-linear systems with fractional derivative excited by Poisson white noise.Chaos， 2016，26（8）:083102

22 Xu Y，Li Y G，Liu D，et al.Responses of Duffing oscillator with fractional damping and random phase.Nonlinear Dynamics， 2013，74（3）:745～753

23 Xu Y，Li Y G，Liu D.Response of fractional oscillators with visc-oelastic term under random excitation.Journal ofComputational and Nonlinear Dynamics， 2014，9（3）:1081～1089

24 Spanos P D，Zeldin B A.Random vibration of systems with frequ-ency-dependent parameters or fractional derivatives.Journal of Engineering Mechanics， 1997，123（3）:290～292

25 Agrawal O P.Analytical solution for stochastic response of a fractionally damped beam.Journal of Vibration and A-coustics， 2004，126（4）:561～566

26 Ghorbanian P，Ramakrishnan S，Whitman A，et al.Nonlinear dynamic analysis of EEG using a stochastic Duffingvan der Pol oscillator model.ASME 2014 Dynamic Systems and Control Conference.American Society of Mechanical Engineers，2014:V002T16A001-V002T16A001

27 Xu Z，Cheung Y K.Averaging method using generalized harmonic functions for strongly non-linear oscillators.Journal of Sound Vibration， 1994，174（4）:563～576

28 Eugene W，Moshe Z.On the relation between ordinary and stochastic differential equations.International Journal of Engineering Science， 1965，3（2）:213～229

29 Diethelm K，Ford N J，Freed A D，et al.Algorithms for the fractional calculus:A selection of numerical methods.Computer Methods in Applied Mechanics and Engineering，2005，194（6-8）:743～773

30 Kai D， Ford N J， Freed A D.A predictor-corrector approach for the numerical solution of fractional differential equations.Nonlinear Dynamics， 2002，29（1-4）:3～22

STATIONARY RESPONSE OF DUFFING-VAN DER POL OSCILLATOR WITH FRACTIONAL DERIVATIVE UNDER GAUSSIAN WHITE NOISE∗

Ma Yanyan Ning Lijuan†
（School of Mathematics and Information Science， Shaanxi Normal University， Xi′an 710119， China）

This paper investigates the stationary response of Duffing-Van der Pol oscillator with fractional derivative damping term under Gaussian white noise excitation.The corresponding Fokker-Planck-Kolmogorov（FPK）equation is firstly deduced by utilizing the stochastic averaging method and Stratonovich-Khasminskii theorem.And we then solve the FPK equation to obtain the stationary probability densities of system amplitude，which in fact can be used to describe the system response.It is then found that the reducing fractional derivative order enhances the system response， while the increasing fractional coefficient weakens the system response.Therefore，the fractional derivative damping term shows a great effect on the response of Duffing-Van der Pol oscillator.In addition， the response is also be influenced by other system parameters.Finally， the above analytical results reasonably fit with that of the Monte Carlo simulation.

response， fractional derivative， Duffing-van der Pol， Gaussian white noise， stochastic averaging method， Monte Carlo simulation

9 September 2016，revised 25 November 2016.

10.6052／1672-6553-2017-060

2016-09-09收到第1稿，2016-11-25收到修改稿.

∗国家自然科学基金资助项目（11202120）和（GK201502007）

†通讯作者 E-mail:ninglijuan＠snnu.edu.cn

∗The project supported by the National Natural Science Foundation of China（11202120） and （GK201502007）

†Corresponding author E-mail:ninglijuan＠snnu.edu.cn