基于空间计量经济学与EKC模型的中国省域环境污染分析

王冠人+言鹏韦

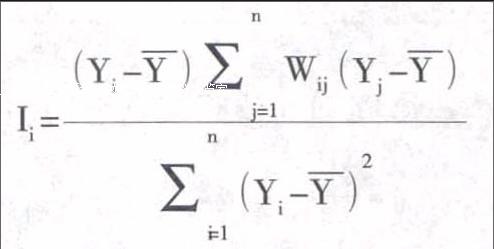
摘 要：当前环境污染日趋严重，怎样在保持经济增长的同时尽可能减少环境污染成本成为热门的话题。环境污染往往与地理空间息息相关，从而可用空间计量经济学对其进行分析。文章依据扩展的EKC模型，截取了2014年我国31个省域有关变量的数据，将其归纳成环境污染、人均GDP等8个变量。值得注意的是，这里将环境污染损失进行了货币化。进而对8个变量进行了全局空间自相关检验与局域空间自相关检验，确定了其皆存在空间相关性，且得到了高—高和低—低集聚区居主导地位的结论。基于Geoda空间统计分析软件，估计了空间滞后模型和空间误差模型，并通过检验确定了我国2014年31个省域环境污染的最优分析模型为空间误差模型（SEM），证实了EKC模型“倒U”型假说。据结果发现我国现阶段各省域人均GDP位于“倒U”型曲线左侧，处于环境污染随着经济增长增加的初级阶段。其中，上海、北京等已临近转折点。同时，文章还分析了各省域人均GDP对环境污染损失的弹性，发现增长1%的人均GDP时，江苏的环境污染损失最小，陕西最大，并分析了造成这种现象的原因。基于上述结论与分析，对环境与经济发展协调给出了综合性的建议。

关键词：空间计量经济学 环境污染 Geoda 库兹涅茨曲线

中图分类号：F205 文献标识码：A

文章编号：1004-4914（2017）06-014-03

一、空间计量经济学环境库兹涅茨曲线模型

1.传统库兹涅茨曲线模型。研究环境污染的传统模型大多基于Grossman{1}提出的库兹涅茨曲线（EKC）模型，模型形式为：

ln（EP）=β0+β1ln（AGDP）+β2（ln（AGDP）2+β3（ln（AGDP）3+ε （1）

模型（1）中，ln（EP）为环境污染的自然对数，ln（AGDP）为人均GDP的自然对数。在吴玉鸣等{3}研究中，基于截面数据，此模型被扩展为：

ln（EP）=β0+β1ln（AGDP）+β2（ln（AGDP）2+β3（ln（AGDP）3+β4ln（POP）+β5ln（URB）+β6ln（HHC）+β7ln（MHC）+β8ln（TTI）+β9ln（FTR）+ε（2）

其中：AGDP表示人均GDP，POP表示年末人口总数，URB表示城市化，用城镇人口占总人口比重衡量，HHC为普通高等教育在校学生数占总人口的比重，近似代表高等级人力资本存量，MHC是中等职业学校在校生数占总人口的比例，近似代表中等级人力资本存量，TTI代表产业结构升级，用第三产业GDP占总GDP比重计算得出；FTR为进出口贸易总额占GDP比重。

2.区域环境污染全局空间自相关检验。对于区域环境污染的空间相关性检验，通常可用空间自相关指数MoransI模型。这里首先对ROOK距离进行说明，它指：如果两者有公共的边界存在，则空间权值W_ij取值为1，否则取值为0。MoransI取值范围为-1到1，如果区域的环境污染存在空间正相关则大于0，区域环境污染存在空间负相关则小于0，区域环境污染空间不相关则等于0。

3.区域环境污染局域空间自相关检验。为了进一步检测区域的环境污染是否存在观测值的局域空间聚集现象以及对于全域空间自相关贡献更大的区域单元、局域非平稳性是否被空间自相关的全域评估掩盖，可通过空间联系的局域指标（LISA）和MoransI散点图{2}进行局域空间自相关分析。

进行区域环境污染的LISA分析需满足两个条件：一是每个区域单元的LISA是描述其周围显著的相似值单元的空间聚集程度的指标：二是所有LISA总和与全局空间联系指标成正比，局域Morans I模型为：

MoransI散点图一般用来探究区域的空间不稳定性。其散点图的4个象限分别对应于区域单元与其相邻单元之间4种类型的区域空间联系形式：第1象限代表区域环境污染观测值高的区域单元包围同是高值的一个区域（简称高—高）；第2象限代表区域环境污染观测值高的区域单元包围一个低值的区域 （简称低—高）；第3象限代表区域环境污染观测值低的区域单元包围一个同是低值的区域（简称低—低）；第4象限代表区域环境污染观测值低的区域单元包围一个高值的区域（简称高—低）。

4.区域环境污染的空间滞后模型（SLM）。考虑到区域环境污染与相邻区域不存在空间相关的假设存在缺陷，本文模型包含了邻近区域环境污染对本区域环境污染的影响，改进常规EKC模型（2）得到空间滞后模型（SLM）为：

ln（EPi）=β0+ρWln（EPj）+β1ln（AGDPi）+β2（ln（AGDPi）2+β3（ln（AGDPi）3+β4ln（POPi）+β5ln（URBi）+β6ln（HHCi）+β7ln（MHCi）+β8ln（TTIi）+β9ln（FTRi）+εi

式中，ln（EPi）是區域环境污染因子，Wln（EPj）为区域环境污染空间的滞后因子，即在地理上相邻的各区域环境污染变量的加权求和值；ρ为空间自回归参数，即相邻区域环境污染对本区域造成的空间影响；β为解释变量回归系数；ε是独立的误差项。

5.区域环境污染的空间误差模型（SEM）。若扰动误差项引起区域环境污染的空间依赖作用，度量邻近区域关于被解释变量ln（EPi）的误差对本区域环境污染的冲击程度的空间误差模型（SEM）为：

式中，φ为n×1的截面被解释变量的空间误差系数，衡量了相邻区域的环境污染因误差项对本区域环境污染的影响方向和程度，β为解释变量回归系数，ε是随机误差项，μ为正态分布的随机误差项。

6.空间自回归模型参数估计。空间依存性的估计比时间序列要复杂得多。空间自回归模型由于自变量的内生性，OLS估计是有偏的和不一致的。因此，如何进行估计一直是计量经济学研究的焦点。上世纪80年代以后，最大似然估计（ML）{3}成为文献中主流方法，最近几年出现的工具变量法（IV）、广义矩估计（GMM）引起了理论界的重视。

二、基于截面数据的中国省域环境EKC模型实证分析

本文按照3.1的模型（2）进行实证分析，但指标的选取与吴玉鸣等{4}的研究中略有不同。其中，EP代表环境污染指数。鉴于固体污染物数据不易获得，此处只考虑水体污染（化學需氧量COD）、气体污染物（二氧化硫，烟尘）和噪声污染，并将其一并货币化来作为环境污染成本。由于碳排放对环境与经济的影响日益明显，所以本文将二氧化碳排放也纳入环境污染指标中。

（一）空间自相关的检验

1.全局空间自相关检验。使用Geoda软件对所有变量进行空间自相关MoransI检验，首先建立ROOK距离权重矩阵，结果显示：

其中与一个省相邻的有1个省（海南），没有周围只有一个省的省份，周围有两个省的省份有4个，周围有三个省的省份有5个，周围有四个省的省份有8个，周围有五个省的省份有3个，周围有六个省的省份有6个，周围有七个省的省份有2个，周围有八个省的省份有2个。

随后对各个变量进行了MoranⅠ检验，这些变量包括ln（EP）、ln（AGDP）、ln（POP）、ln（HHC）、ln（MHC）、ln（URB）、ln（FTR）。假设各邻近省域之间的环境污染及其决定因素不存在空间自相关性，利用重复随机排列法排列999次，构建标准正态统计量，根据ROOK空间权值矩阵计算的MoransI指数均大于0，p-value均大于0.016，这表明所有的EKC模型中的变量在空间分布中均存在明显的正自相关关系，可见在研究省域环境污染时空间效应不可忽略。

2.局域空间自相关检验。使用Geoda进行局域LISA自相关检验，结果显示：新疆自治区的显著性小于0.001，四川、山东和安徽等省的显著性小于0.01，青海、江苏、福建和江西等省显著性小于0.05。其他省份显著性均大于0.05。

此外，由MoranⅠ的散点图发现我国各省域环境污染表现出明显的空间依赖性，大多数省域集群在第一象限和第三象限：即较高环境污染的省区相对趋于和较高环境污染的省区靠近（第一象限）。这些省域是：上海、安徽、福建、山东、江苏、北京、河南、河北、浙江、湖南、湖北、辽宁、广东。较低环境污染的省区相对趋于和较低环境污染的省区靠近（第三象限），这些省域是：新疆、青海、甘肃、西藏、宁夏、云南。不难发现，这些高污染集群区域，皆为我国东、中部经济发达和人口稠密区域。轻度污染集群区域皆为我国西部内陆经济发展相对落后区域。

（二）空间计量模型的估计与分析

本文对SEM和SLM模型采用极大似然法进行参数估计并进行了模型的LM检验，此外还进行了回归诊断。检验结果如下：比较对数似然函数logL、赤池信息准则AIC和施瓦茨信息准则SC值发现，SEM的logL值大于SLM，且SEM的AIC和SC值也小于SLM，故依据logL、AIC和SC值做出推断：SEM模型较之SLM模型更好。此外，依据表中较之LM （error）显著，且Robust LM（error）显著而LM（lag）不显著，最后断定SEM模型要优于SLM模型，最终回归模型为：

人口规模（lnPOP）的回归系数为0.9789，说明固定其他因素，人口规模每增长1%，环境污染损失将增长0.9789%。人口数量的增长通常导致经济活动规模扩大，对环境保护施加外部压力。对于东部地区环境较差，人口密度过高难脱干系；同样西部地区环境污染较轻，得益于其人口稀少。

城市化（lnURB）的回归系数为0.2795，说明环境污染问题较大程度上归咎于城市化推进。城市发达的交通系统方便了居民出行，但也造成了二氧化碳等污染气体的过量排放；此外城市内还存在工业噪声、建筑噪声等，严重污染了城市环境。

产业结构（lnTTI）的回归系数为-0.0779，说明第三产业发展拉动产业结构优化，减轻了环境污染。

高等级人力资本（lnHHC）与中等级人力资本（lnMHC）的回归系数分别为-0.0324和0.0402，通过了6%和5%的显著性检验。这说明增加高等级人力资本有助于缓解环境污染。其他因素不变，高等级人力资本每增加1%，环境污染损失减少0.0324%。而中等级人力资本积累却加速了环境污染，其增加1%会导致环境污染损失增加0.0402%。高等级人力资本能高效地吸纳和应用新技术，激发技术创新与进步，从而摆脱粗放型经济增长方式，减轻环境污染。中等级人力资本普遍在第二产业或技术含量低的生产领域从事经济活动，因此中等级人力资本同环境污染之间呈正相关。

对外开放ln（FTR）的回归系数为-0.029，且P<0.001，说明对外开放程度的提高可减轻环境污染。贸易开放的技术外溢效应提高了发展中国家的要素生产率，从而间接地通过促进技术进步和产业结构调整而减少污染排放。

三、结果分析

利用MATLAB拟合lnEP与lnAGDP得到2014年中国31个省域的截面数据拟合图。图形显示，我国省域EKC曲线拟合图形呈现“U+倒U型”，偏离“倒U型”曲线不是很明显，证明EKC曲线“倒U型”假说在我国省域间有较强适用性。将（4）式对lnAGDP求导得：

令=0，得第一个转折点lnAGDP1=-14.0992， lnAGDP2=14.0881，根据计算出的2014年我国各省的lnAGDP可知，最大为上海lnAGDP=11.5863，最小为贵州lnAGDP=10.1824，全部31个省域的lnAGDP都分布在第一个转折点与第二个转折点之间，在此阶段，曲线呈向右上升阶段，表明人均GDP越高的省域环境污染损失越严重。其中上海，北京，天津等较接近第二转折点，正朝着随着人均GDP增加，环境污染损失减少的阶段迈进。

此外，笔者还计算了2014年中国31个省域lnAGDP对lnEP的点弹性和2014年中国31个省域第一三产业占比，其中点弹性最小的是江苏为1.3172，表示人均GDP每增加1%会导致环境污染损失增加1.3172%；点弹性最大的是陕西为2.8885，表示人均GDP每增加1%会导致环境污染损失增加2.8885%。由于在第一，二，三产业中，带来环境污染的主要是第二产业，所以第一，三产业占比越低，第二产业占比越高，环境污染损失对GDP增长弹性越大，而陕西正好是第二产业占比最高的省域。

四、结语

本文基于空间计量经济学环境库兹涅茨曲线模型、区域环境污染的空间滞后模型（SLM）以及区域环境污染的空间误差模型（SEM），对我国各个省域的环境污染状况进行了分析。模型的结果显示：人口规模增加和城市化这两个因素对环境污染的影响最大。同时本文证明了EKC曲线的“倒U型”假说在我国省域间有较强适用性，全部31个省域的lnAGDP都分布在第一个转折点与第二个转折点之间，即人均GDP越高的省域环境污染损失越严重，最接近第二个转折点的省份有上海、北京和天津。此外，我们还计算出了人均GDP每增加1%会导致环境污染损失增加的最多和最少的省份分别为陕西和江苏。

注释：

{1}Jams LeSage，R. Kelley Pace.Introduction to Spatial Econometrics[M].北京大学出版社，2014

{2}公云龙，张绍良，章兰兰.城市地价空间自相关分析——以宿州市为例[J].经济地理，2011（11）

{3}刘毅.具有空间相依误差的面板数据自回归模型及参数估计的统计计算实现[D].四川大学，2007

{4}吴玉鸣，田斌.区域环境库兹涅茨曲线的扩展及其决定因素[J].地理研究，2012（4）

（作者单位：中南大学数学与统计学院 湖南长沙 410083）

（责编：吕尚）