浅谈数形结合思想在解题中的应用

吴胜珍

【摘 要】数形结合思想是数学解题过程中非常重要且好用的指导思想，在数学的广袤领域中，数与形可谓左膀右臂，彼此相辅相成。数与形各有其优点，也各有其不足之处。巧妙应用数形结合思想，不言而喻，在解题中将易做到巧解，快解，进而提高解题效率。

【关键词】数形结合；解题；应用

数与形是数学问题中的两大模块，两者看似有着天壤之别，实则息息相关。数是抽象繁琐的代码，通过形的转化可将之形象化，通过对图形的观察发现潜在规律，从而找到更加快捷的解题途径。而对于一些复杂的图形，通过数的转化，可将复杂难解的几何问题简单化成单纯的代数运算，从而省去大把寻找解题思路的时间。由此观之，数与形各有千秋，数形结合思想若能熟练掌握、巧妙应用，将是解题中的一大利器。

掌握数形结合思想，要求我们对代数式的结构有充分的分析、变形、联想能力，对形的几何特征、几何意义有深入的挖掘和准确的把握，要树立数形一体的思维框架，这及其考验一个学生的数学修养。

一、数形结合和不等式

一些复杂的不等式的题目，若直接从代数角度出发寻找解题思路往往费解甚至走进死胡同。此时若能下意识的观察代数式的结构特征，往几何方向联想，往往会有柳暗花明之感。

例题一：设x、y、z为正数，求证+>

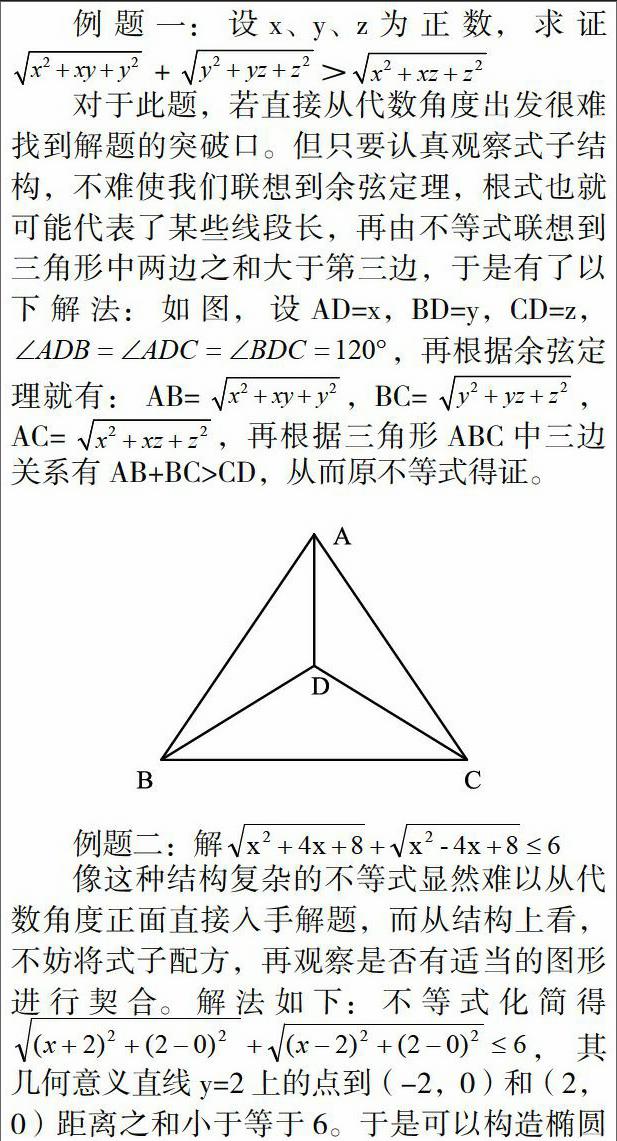
对于此题，若直接从代数角度出发很难找到解题的突破口。但只要认真观察式子结构，不难使我们联想到余弦定理，根式也就可能代表了某些线段长，再由不等式联想到三角形中两边之和大于第三边，于是有了以下解法：如图，设AD=x，BD=y，CD=z，，再根据余弦定理就有： AB=，BC=，AC=，再根据三角形ABC中三边关系有AB+BC>CD，从而原不等式得证。

例题二：解

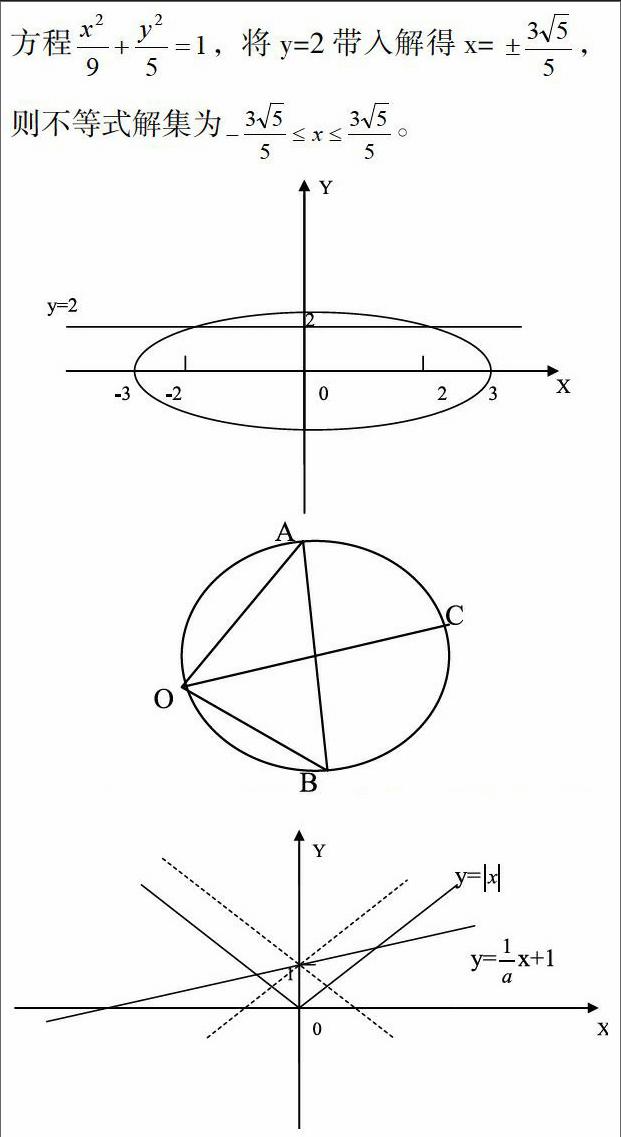
像這种结构复杂的不等式显然难以从代数角度正面直接入手解题，而从结构上看，不妨将式子配方，再观察是否有适当的图形进行契合。解法如下：不等式化简得，其几何意义直线y=2上的点到（-2，0）和（2，0）距离之和小于等于6。于是可以构造椭圆方程，将y=2带入解得x=，则不等式解集为。

通过以上的两个例题我们可以发现，解决复杂的不等式问题，走数形结合的道路往往趋利避害、事半功倍。这就要求我们对于式子的结构有深入的剖析，对式子的变形技巧灵活掌握，对常见的两点距离公式、点线距离公式、圆锥曲线定义及方程等知识点有全面的掌握，同时兼备有丰富的联想能力。

二、数形结合与向量

向量是数学中的一个独特的工具，因为它具备基底形式的转化和运算，又具备坐标方面的代数运算，因此，向量常常被作为连接代数和几何的桥梁，数形结合的思想在解决向量的题目中往往是一把利刃。

例题三：已知a，b是平面内两个互相垂直的单位向量，若向量c满足（c+a）·（c-b）=0，则|c|的最大值是？

此题无论从基底还是坐标的角度都十分费解，但是如果能够抓住题干中的众多垂直关系加以利用，构造适合的图形观察几何特征就会发现更加快捷的解题途径。解法如下：如图做向量OA⊥OB，记向量OA，OB分别为a，b，根据直径对应的圆周角为直角，则向量c为以O为起点，终点在以AB为直径的圆上记作C，易得该圆直径为，则|c|取最大值时即OC为直径时。|c|最大值为。

不仅仅是平面向量，数形结合在空间向量中的应用也同样简便，尤其是在解决立体几何的题目中。在计算空间角、证明平行、垂直等位置关系中，化空间关系为简单明了的向量坐标运算，将会大大减轻解题负担。

三、数形结合与函数

函数作为中学阶段的一个重要且热门的考点，将数形结合的思想体现的淋漓尽致。函数的特殊性在于它兼具了图像和方程两个性质。函数的图像将函数独有的单调性、零点、极值、最值、渐进等各项几何特征以最直观的方法表现出来，便于我们做出草图，进行初步的定性分析。而要做一些精确的定量，就需要借助方程，从代数角度运算。正如华罗庚所言：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”只有掌握好数形结合的思想，才能将复杂多变的函数问题系统化，才能将函数研究清楚。

通过函数的几何特征求一些未知数的值或者取值范围是函数一类常考的题型，这就需要我们做出适当的草图，寻找几何关系，列出方程或不等式求解。

例题四：函数y=a|x|与y=x+a的图象恰有两个公共点，则实数a的取值范围是（ ）

对于两个函数均存在未知数的情况存在太多变的因素，我们不好直接画出其图像，因此可对两者进行适当的变形。易得a=0时不符合题意，因此将a|x|

=x+a转化|x|=x+1。则问题就变成新的函数y=|x|和y=x+1有两个交点。画出两者图像，即可找出临界位置是平行位置，再计算得出C选项。

除此之外，在函数中求解恒成立问题、存在性问题等大题，甚至在一些复杂的三角函数值域及倒数问题中，数形结合思想往往作为主导思想贯穿着整个解题思路，形的不确定性、未知数取值变化的影响往往被作为分类讨论的依据，因此，数形结合思想在解决函数问题中的重要作用可见一斑。要掌握数形结合的方法、解决好函数千变万化的题目，要求我们对各项初等函数的图像及其特征充分把握，对未知数取值的影响有全面深入的分析。

四、数形结合与数列

像数列这种看似纯粹研究数的模块中，数形结合思想仍然发挥着举足轻重的作用。就拿特殊数列——等差数列来说，其前n项和的表示式经化简为Sn=An2+Bn形式，就发现它的所有点是经过原点的抛物线上的点。于是对等差数列最大、最小项，以及对其前n项和最值、相等项的研究，就可以转化成对二次函数图像的研究，而借助二次函数图像的对称性，就可以达到巧解、速解的效果。

例题五：等差数列{an}中，a1>0，S6=S10，则（1）n= 时，Sn取得最大值（2）S16= 。

如果知道借助二次函数图像求解，此题将十分容易：由于等差数列前n项和可写成Sn=An2+Bn的形式.由已知S6=S10可知对应的二次函数的对称轴应是x=8，且公差小于零，开口向下，有最大值.于是可知n=8时，Sn取得最大值.因为二次函数图像过原点，所以过点（16，0），即S16=0。

变式：等差数列{an}中，S9>0，S10<0，则当n= 时，Sn最大。

分析如下：设二次函数与x轴的另一个交点为（m，0），则m∈（9，10），所以对称轴为x=∈（4.5，5），靠近5，因此当n=5时，Sn取最大值。

可见，及时是在数列中，图形的应用也是非常灵活巧妙的，这也印证了美国图论学者哈里的一句话：“千言万语不及一张图。”

五、数形结合与概率

数形结合思想甚至可以渗透到概率领域。最为典型的就是几何概型。但是在解决一些复杂实际问题时，人们就往往会遗忘形的辅助作用。其实，借助适当图形解决概率问题，可能会使得抽象复杂的问题更加明了直观。

例题六：甲、乙两人约定在晚上7时到8时之间在公园门口会面，并约定先到者应等候另一个人15分钟，还未来即可离去，那么两人能见面的概率是多少？

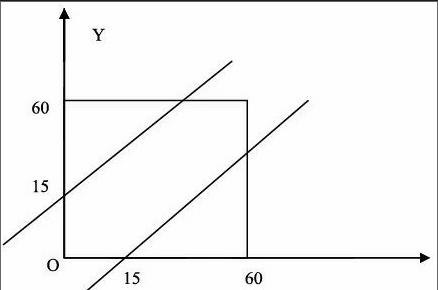
此题的情景看似简单，但是如果不借助图形，实际上费解也易错。此时，图形的优越性就得到了充分的体现：如图，以x轴和y轴分别表示甲、乙两人到达约会地点的时间，那么两人能见面的充要条件是|x-y|≤15。（x，y）的所有可能结果组成的图形是边长为60的正方形，能见面的时间由图中两平行线之间部分所表示。由此便可輕松计算出所求概率P=。

综上对各类题目的分析，我们不难发现，数形结合思想在数学中的适用性是及其广泛的。数学并不仅仅是研究“数”的一门学科，也是研究“形”的一门学问。数与形，两者息息相关，如同工匠的左膀右臂，相辅相成，才能构建一座富丽堂皇的数学城堡。其实，数形结合思想远不止局限在不等式、向量、函数、数列、概率等问题，它可能渗透到数学所能涉及的各个领域，熟练掌握数形结合，将会对我们的解题产生莫大的帮助。而要想培养一个人的数形结合思想，就必须要有丰富的知识储备，有广阔缜密的思维，要善于联想，突破常规思维的限制，这就及其考验一个人的数学修养。

总而言之，数形结合思想有其显著的优越性和广泛的适用性，它是解决各项数学问题的一把利刃，掌握它，在解题过程中将如虎添翼！