分布式驱动电动汽车驱制动系统容量分配方法

张立军，李濯宇，孟德建

（1.同济大学 汽车学院，上海 201804；2.同济大学 智能型新能源汽车协同创新中心，上海 201804）

分布式驱动电动汽车驱制动系统容量分配方法

张立军1,2，李濯宇1,2，孟德建1,2

（1.同济大学 汽车学院，上海 201804；2.同济大学 智能型新能源汽车协同创新中心，上海 201804）

针对现有分布式驱动电动汽车驱、制动系统容量分配多采用四轮平均分配的问题，提出了一种驱、制动系统轴间容量分配的方法。其中，基于动力性的驱动系统前后轴容量分配的目的是改善最大加速度、最大爬坡度和百公里加速时间；基于制动性的电液复合制动系统前后轴容量分配的目的是改善制动距离和平均制动减速度。分析结果表明，提出的驱、制动系统容量分配方法有效改善了车辆的动力性和制动性。

电动汽车；分布驱动；驱动系统；制动系统；容量分配

安全、节能、环保、舒适是汽车发展的永恒主题，电动化和智能化是全球公认的汽车技术前沿领域［1］。采用轮毂电机或轮边电机驱动的分布式驱动电动汽车，结构紧凑、传动效率高，且能通过独立、快速、精确的电机控制实现各车轮驱动力与制动力的控制，兼具动力电动化和安全智能化的技术特征，已成为业界关注的焦点和热点［2］。

现有分布式驱动电动汽车驱、制动系统轴间容量分配主要采用四轮平均分配的方法，未充分考虑加速及制动时载荷转移效应的影响，也未能利用分布式驱动电动汽车各车轮力矩独立可控的技术优势改善整车动力性和制动性。同时，现有研究和文献多着眼于驱制动力的轴间动态分配控制策略［3-4］，较少关注利用驱、制动系统轴间容量分配改善整车动力性和制动性［5-6］。因此，有必要研究如何通过合理分配轴间容量改善整车的动力性和制动性。

本研究以改善整车动力性和制动性为目标，分别设计了基于动力性的驱动系统轴间容量分配方法和电液复合制动系统轴间容量分配方法，并对该方法进行分析和验证。

1 驱、制动系统总容量匹配

采用某车型的参数模型进行研究，其相关参数见表1。

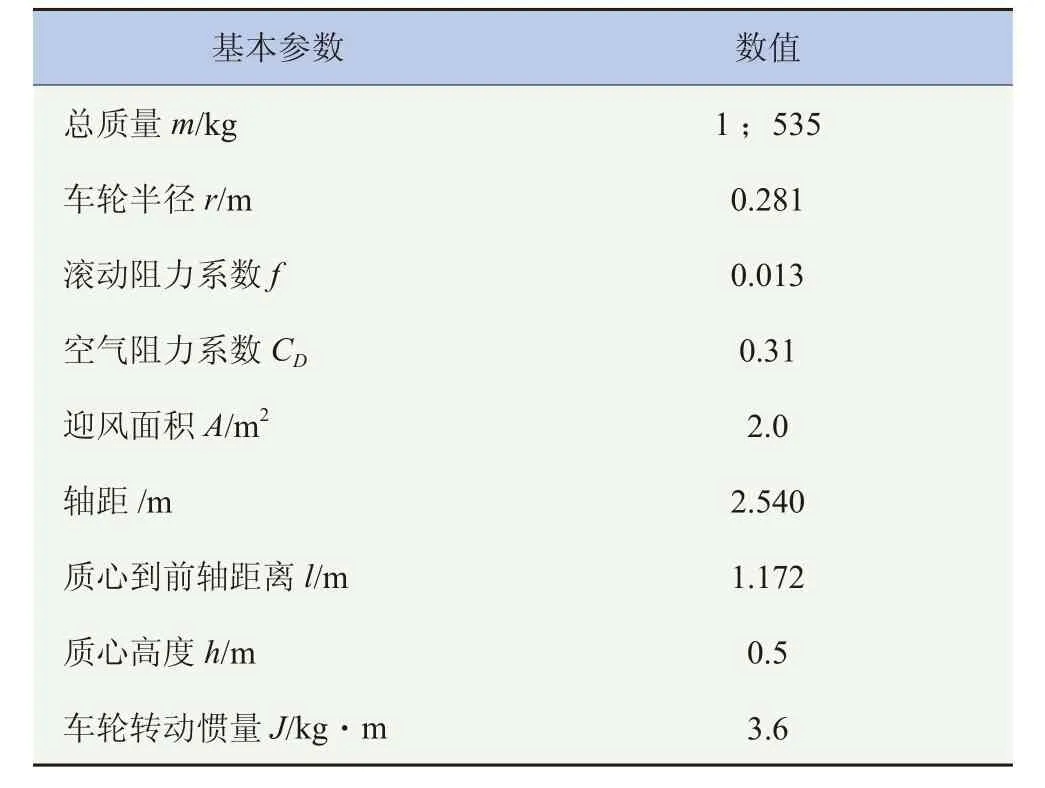
表1 车型主要参数

下面分别针对动力性和制动性指标进行驱、制动系统总容量的匹配。

1.1 驱动系统总容量匹配

整车需要达到的动力性指标见表2。

表2 动力性指标

最大车速对应电机的持续工作区［7］，据此匹配电机额定功率Pe和最大转速nmax：

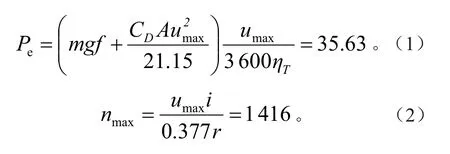
式中：m为总质量；f为滚动阻力系数；CD为空气阻力系数；A为迎风面积；umax为最大车速；ηT为传动效率；i为传动比，此处取i=1；r为车轮半径。

最大爬坡度对应电机的短时工作区，据此匹配电机的最大转矩Tmax：

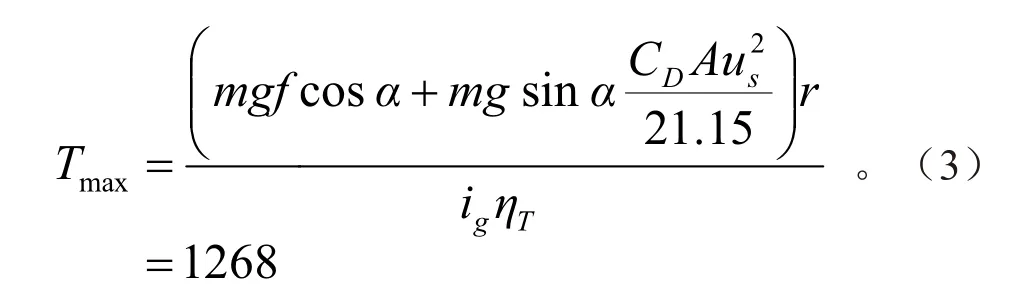
百公里加速时间也对应电机的短时工作区：

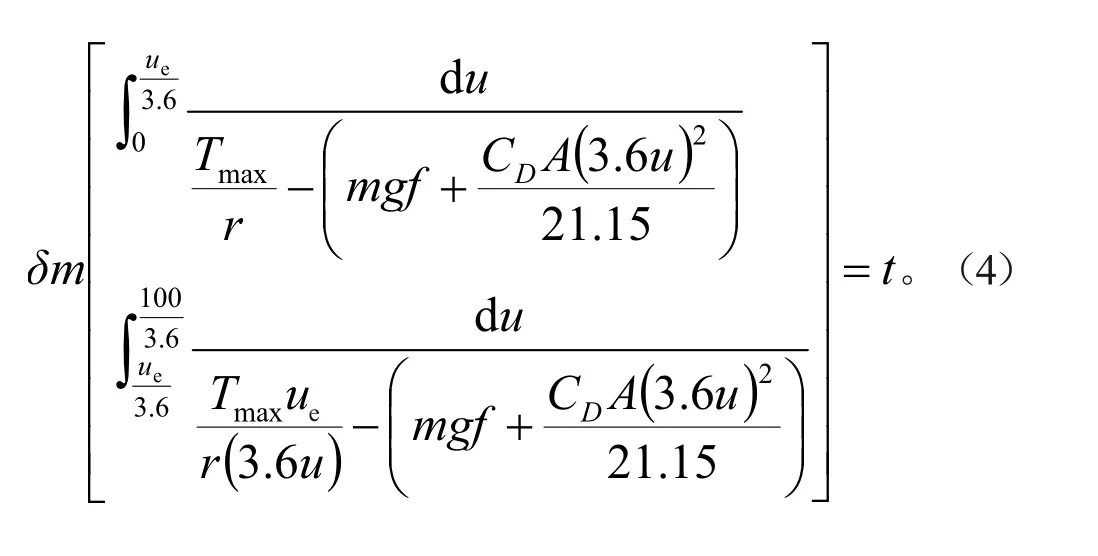
此时Tmax=1 419 Nm。与最大爬坡度匹配出的最大转矩相比，取大者。此外，电机的转速比取1.875［8］。

以上匹配出了驱动电机的总容量参数，经过数据圆整，得到电机实际参数见表3。

表3 驱动系统总容量参数

1.2 制动系统总容量匹配

根据国标《GB 21670—2008 乘用车制动系统技术要求及试验方法》，结合所选车型的参数，得到制动性指标见表4。

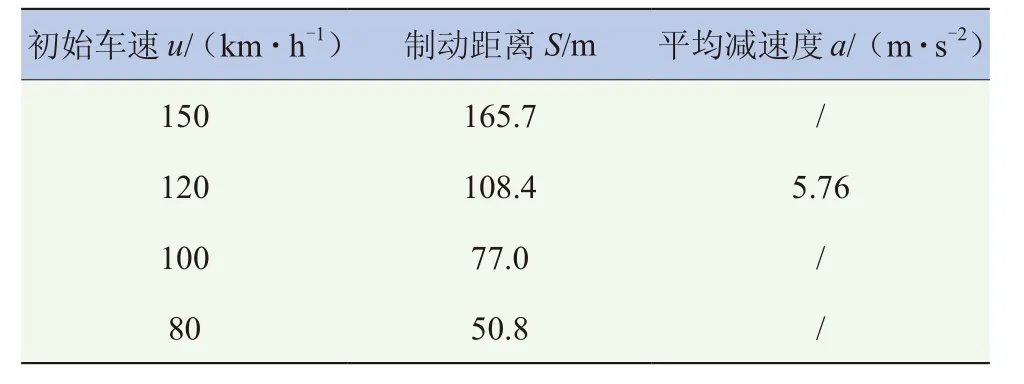
表4 制动性指标

根据制动距离和平均减速度要求匹配总制动容量，总容量与电机再生制动容量之差即为所需液压制动容量［9］。制动距离计算公式如下［10］：

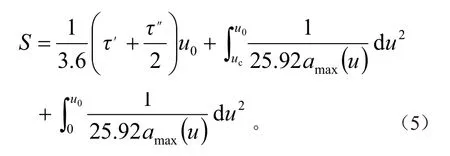
式中：τ′+τ″/2为制动器作用时间，取0.4 s；u0为制动初速度；uc为常规车速。

平均减速度计算公式如下：

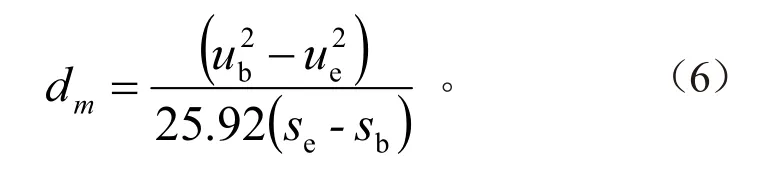
式中：ub=0.8u0；ue=0.1u0；sb为u0到ub车辆经过的距离；se为u0到ue车辆经过的距离。

按表3取不同的制动初速度进行计算，最终匹配出所需液压制动容量为Th=1 535 Nm。因此，制动系统所能产生的最大制动力与车速的关系如图1所示。

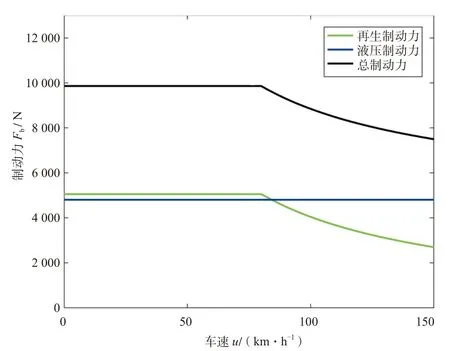
图1 制动系统最大制动力曲线

下面以所匹配的驱、制动系统总容量为基础，研究驱、制动系统容量轴间分配对整车动力性和制动性的影响及优化方法。

2 驱动系统容量分配优化方法

定义电机容量分配比βD为汽车前轮电机最大转矩占前后轮电机总转矩的比例：

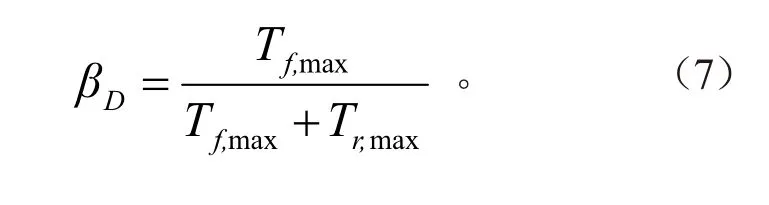
取值范围为0 ≤ βD≤ 1。

βD值的变化关系到前后轮驱动电机最大转矩的变化，μ值的变化关系到路面附着力的变化，因此需要通过βD和μ的联合变化，在多种情况下比较电机驱动力与路面附着力的大小关系，得出该情况下的实际驱动力，进而得出相应的最大加速度、最大爬坡度和百公里加速时间等参数的解析式。

下面以最大加速度为例，简要说明动力性参数解析式的具体推导方法。本文默认采用计入了坡度阻力、空气阻力等行驶阻力影响的完善I/f/r线组公式［11］，如式（8）～（10）所示。

I曲线：

式中：α为路面坡度角；hg为整车质心高度；Lf为质心到前轴距离；Lr为质心到后轴距离；Fdf为前轮驱动力；Fdr为后轮驱动力；μ为 路面附着系数；且p=f（hg-r）。

2.1 对最大加速度的影响

2.1.1 解析式推导

考虑最大加速度，则车速和路面坡度均取为0，其余参数按表1和表3取值。

由于电机总功率确定，前后轴总驱动力为定值。作电机驱动力线及不同μ值的f / r线组，如图2所示。

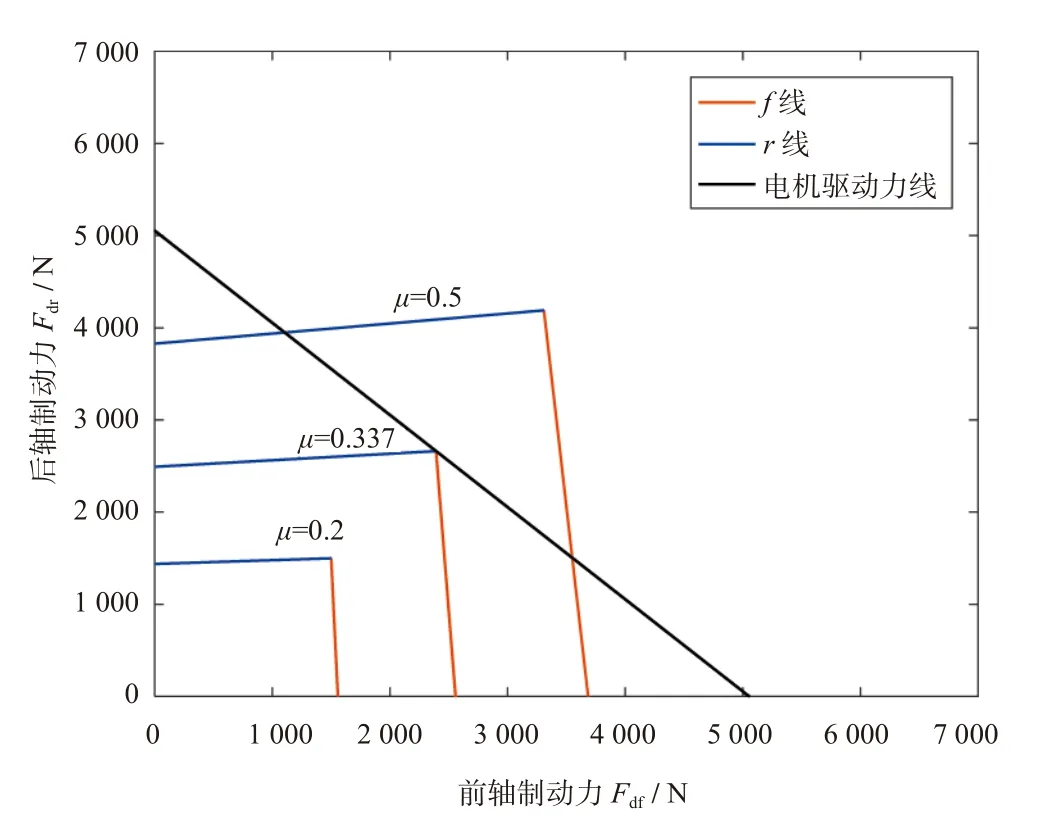
图2 不同μ值的f / r线组

由图2可知，随着μ值的变化，f / r线组与等驱动力线之间的相对位置关系也是发生变化的，图中第二组f / r线即为μ的临界情况，定义该情况下的μ值为μ的临界值。因此可按照以下步骤进行分区间讨论：

（1）求出μ的所有临界值μ0，μ1，μ2…并依此划分出若干个区间。

（2）在μ的每个区间里，再视具体情况对βD进行区间划分。例如μ0＜μ＜μ1时如图3所示，图像根据βD划分成了Ⅰ，Ⅱ，Ⅲ三个区间。

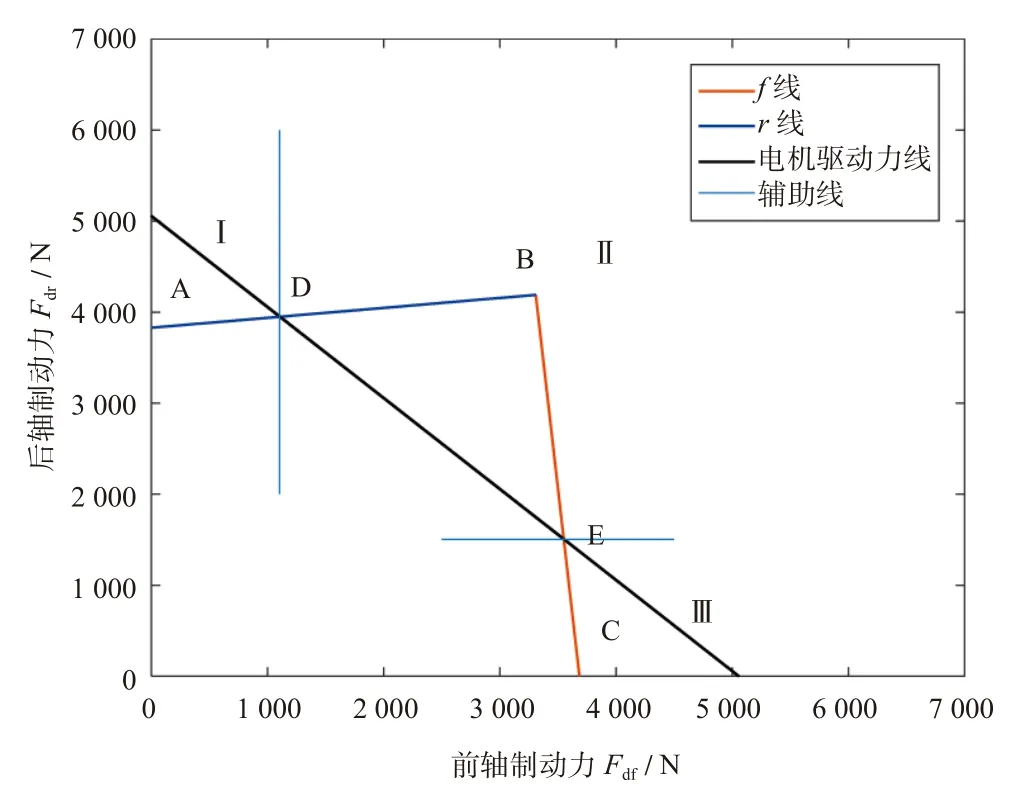
图3 根据βD划分区间

（3）在βD的每个子区间内，比较电机驱动力和路面附着力的相对大小，给出实际最大驱动力解析式并绘制图像，如图4所示。

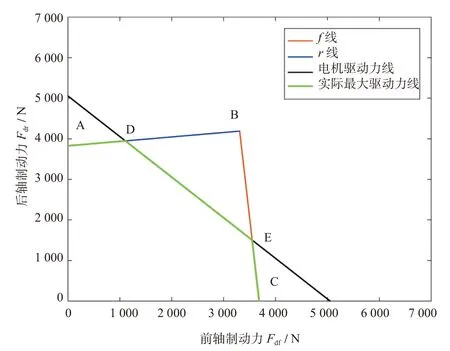
图4 实际最大驱动力

（4）根据各区间内的实际最大驱动力公式，计算出相应的最大加速度解析式。

按上述步骤，即可推导出0≤μ≤1与0≤βD≤1联合变化的所有情况下的最大加速度解析式，形成完整的公式组。

2.1.2 数值分布与最优方案选取

根据最大加速度公式组，可绘制最大加速度随βD和μ变化的三维图像，如图5所示。

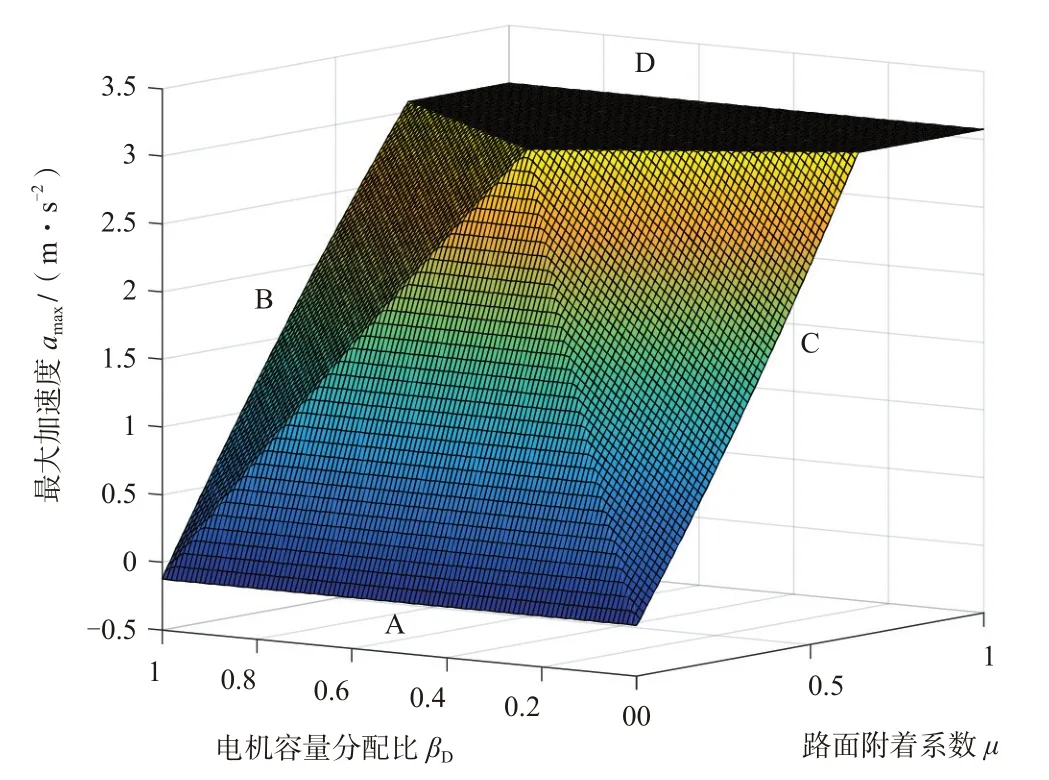
图5 最大加速度

该图反映了分布式驱动电动汽车所有可能的电机容量分配方式下，整车所能达到的最大加速度的变化情况。该图与μ-αmax面的两条截距线，即为前轮驱动和后轮驱动两种传统两驱布置方式的加速度变化曲线，βD=0时如图6所示。

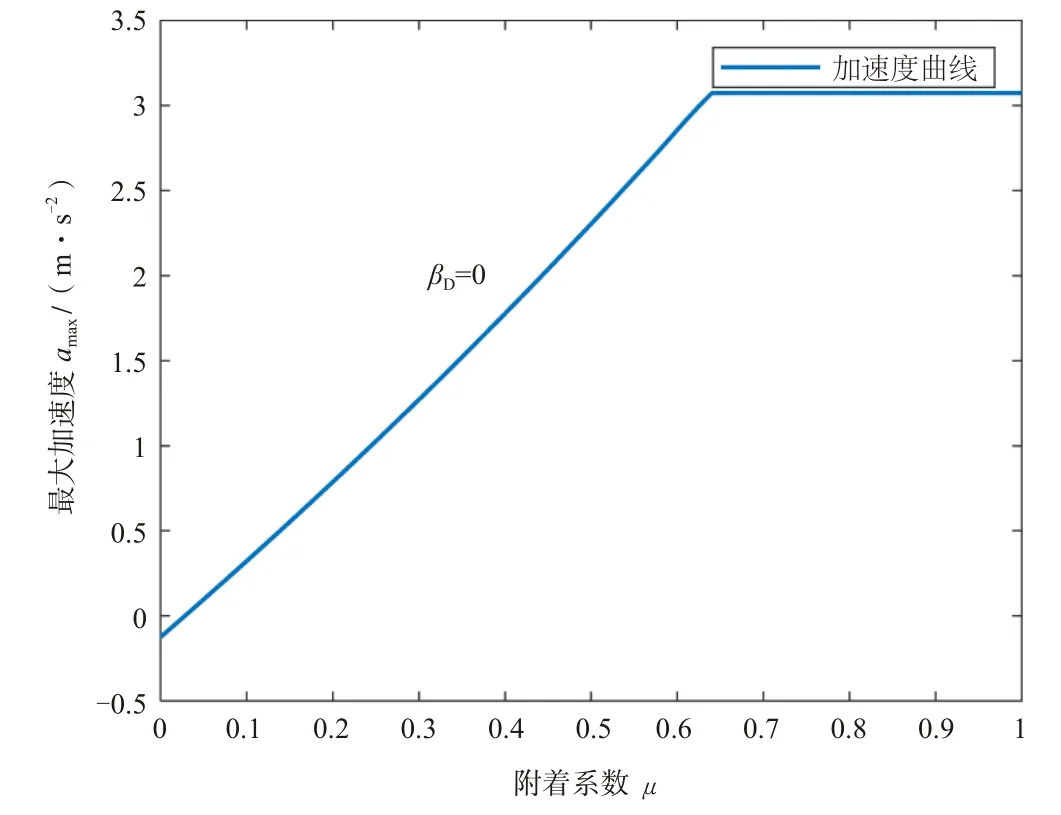
图6 后驱加速度曲线

可以看出，当βD=0时，最大加速度随着μ逐渐增大，直到μ=0.63时才达到最大值3.07 m/s2（约为0.31 g），整车的路面附着系数利用率仅为49%，证明了两轮驱动的局限性。

另一方面，对照图中细直线可以看出，加速度并非线性增大，而是沿着斜率逐渐变大的曲线上升。这是由于随着最大加速度值的增大，对应的驱动强度也在增大，使整车的轴荷发生后移，后轴分配的轴荷比例逐渐增大。由于此时电机全部布置在后轴上，所以随着后轴的加速能力越来越强，最大加速度增长的斜率逐渐增大。这也说明了图5中的C、D区域是曲面而非平面。

观察图5中最大加速度的变化趋势，当路面附着系数μ较小时（图中μ ＜0.33），在βD轴的两端（C、D区域），图像变化趋势对称，整车最大加速度值较小，有车轮处于打滑状态，即电机驱动力大于路面附着力；βD轴中段（A区域）的最大加速度值较大，但由于路面附着条件限制，电机驱动力仍未全部发挥作用；在βD=0.48附近，最大加速度达到最大值。当μ较大时（0.33 ≤μ≤ 0.68），在βD轴中段（D区域），最大加速度可以达到最大值。当μ足够大时（μ ＞0.68），对于任意βD，最大加速度始终可以达到最大值。

考虑上图中各点的附着系数利用率，如图7所示。

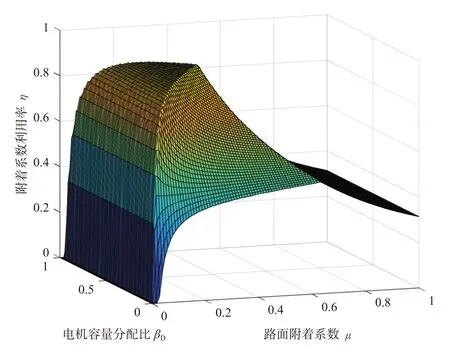
图7 附着系数利用率

可以看出，在βD=0.48附近，附着系数利用率较大。而图5中D区域所示位置则表明，一旦电机驱动力全部发挥作用，则路面附着系数越大，附着系数利用率越低。

综上所述，在本模型的参数下，按照四轮驱动的方式来布置电机，并使前后轮的电机容量按照0.48∶0.52来分配，可使整车的最大加速度达到最优化。

2.2 对最大爬坡度的影响

考虑最大爬坡度，规定汽车以us=10 km/h的速度匀速爬坡，不考虑加速阻力，且空气阻力Fw为定值。设汽车所能达到的最大驱动力为Fd，则：

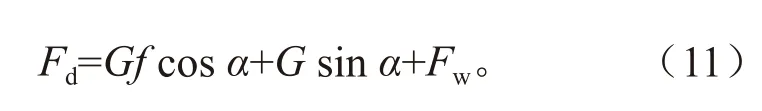
由此计算出最大爬坡度。在不同电机容量分配比βD和附着系数μ的条件下，最大爬坡度公式的推导过程和最大加速度公式完全一致，所得最大爬坡度随βD和μ变化三维图的变化趋势也与图5一致，不再赘述。

需要注意，由于在分区间讨论时，区间边界的解析式可能包含坡度角α，因此需要预设一个坡度角来帮助确定区间边界，导致各区间边界存在一定的误差，但对最大爬坡度的数值和变化趋势影响极小。

2.3 对百公里加速时间的影响

百公里加速时间的研究过程与最大加速度类似。但由于常规车速取为80～100 km/h，因此当u ＞80 km/h时，电机由恒转矩阶段进入恒功率阶段，随着车速上升，转矩开始下降并且转矩T是车速u的函数。至u =100 km/h时，转矩为T=Tmin=1 136 Nm。因此电机驱动力线不是唯一的，分区间讨论的过程更加复杂。下面对推导过程中与前述两个参数的不同之处作简要说明。

2.3.1 解析式推导

考虑百公里加速时间，设路面为水平。取不同的μ值作f / r线组及两条电机驱动力线，得到μ的多个临界值，并依此划分区间。在每个μ的区间内，再对βD进行分区间，如图8所示。

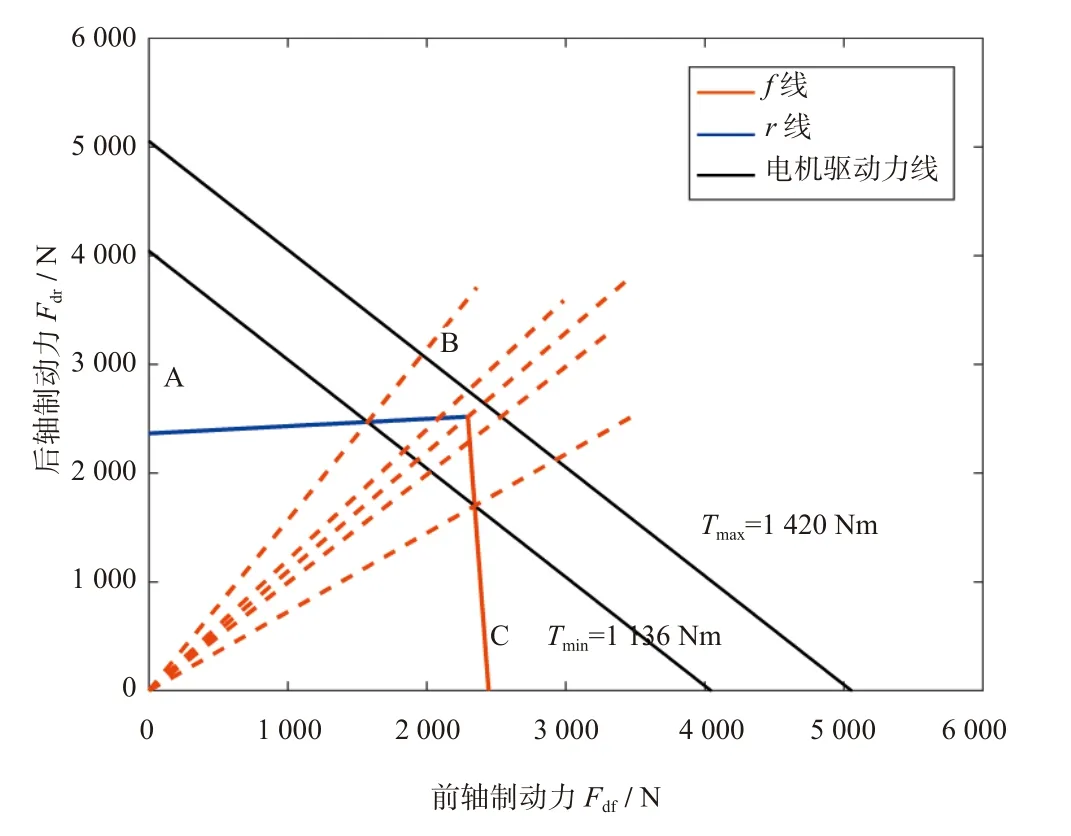
图8 对βD划分区间

由于车速是变化的，因此在每一个βD的区间内，还需要再对车速进行分区间讨论，即按照“μ→ βD→ u”的次序分3层进行讨论，最后给出每个子区间内百公里加速时间的解析式。

2.3.2 数值分布与最优方案选取

根据百公里加速时间公式组，可绘制出百公里加速时间随βD和μ变化的三维图，如图9所示。

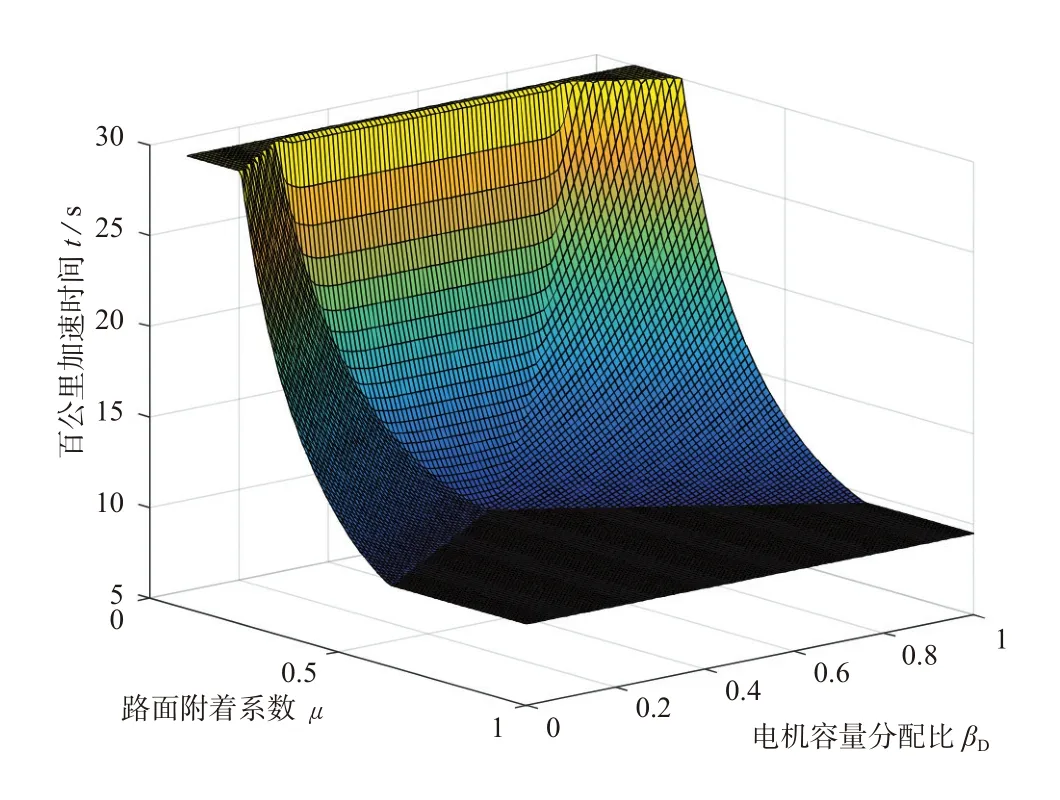
图9 百公里加速时间

上图的变化趋势与最大加速度、最大爬坡度图像基本呈对应关系，前后容量分配比也取为0.48∶0.52最佳。当μ足够大时，百公里加速时间的稳定值为9.5 s，与最初设计要求一致。

2.4 最优化分配方法

综合最大加速度、最大爬坡度和百公里加速时间3个动力性参数的变化规律可以得出，在当前轿车模型的参数下，电机容量分配比βD取0.48，即前后电机容量按照0.48∶0.52来分配时，上述三个动力性参数均为最优化结果，对整车的动力性最为有利。当车型参数改变时，按照上述方法，同样可以找出相应的最优容量分配比。这为四轮驱动电动汽车的前后驱动容量分配提供了一种最优化的方法，比四轮容量平均分配布置方法更加合理。

3 制动系统容量分配优化方法

仿照电机容量分配比βD，定义液压制动容量分配比βB。因此在制动过程的研究中，有3个自变量：（1）电机容量分配比βD。（2）液压制动容量分配比βB。（3）路面附着系数μ。由于在考虑制动容量前后分配对整车制动性能的影响时，不涉及电机制动和液压制动之间的协调分配问题，二者对整车的制动效果没有区别。因此，为了简化讨论，引入总制动容量分配比βT，表示前轴总制动容量占前后轴制动总容量的比例：

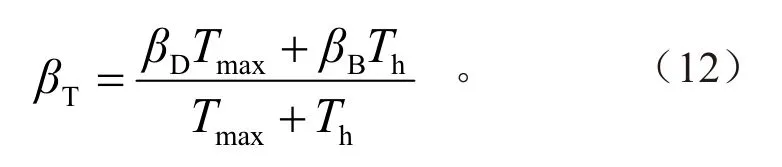
显然0 ≤ βT≤ 1。下面讨论总制动容量分配比βT以及路面附着系数μ的变化对制动距离和平均减速度的影响规律［12］。

3.1 对制动距离的影响

制动距离公式组的推导方法和百公里加速时间类似，即按照“μ → βD→ u”的顺序分3层进行分区间讨论，最后采用解析方法给出每个子区间内制动距离的公式。

需要注意的一点是，在车速u超过80 km/h后，电机再生制动的容量会变小，但液压制动容量保持不变，因此公式中应使用T=80Tmax/u+Th项。初速100 km/h时的制动距离随βT和μ变化的图像如图10所示。

可见，制动距离的变化规律与百公里加速时间类似，但βT的最优取值在0.66左右。

设驱动系统容量分配比取最优值βD=0.48，根据式（12）将βT换算为液压制动容量分配比βB，即可得到制动距离与βB的关系，如图11所示。则可以看出，仅对液压制动系统的布置而言，当液压制动容量分配比βB在0.85左右时，整车制动性最优。

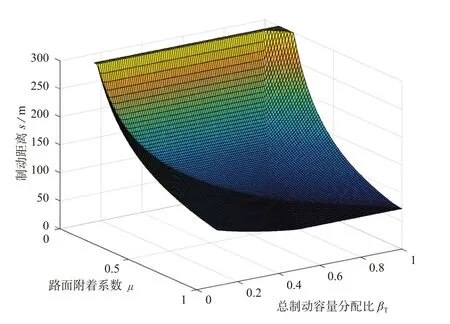
图10 初速100 km/h的制动距离

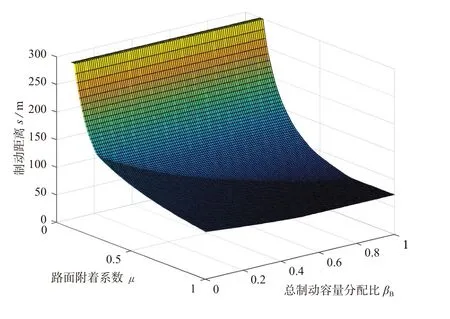
图11 初速100 km/h的制动距离（βB作横轴）

3.2 对平均减速度的影响

平均减速度公式的推导过程与制动距离类似，给出平均减速度随βT和μ变化的图像，如图12所示。

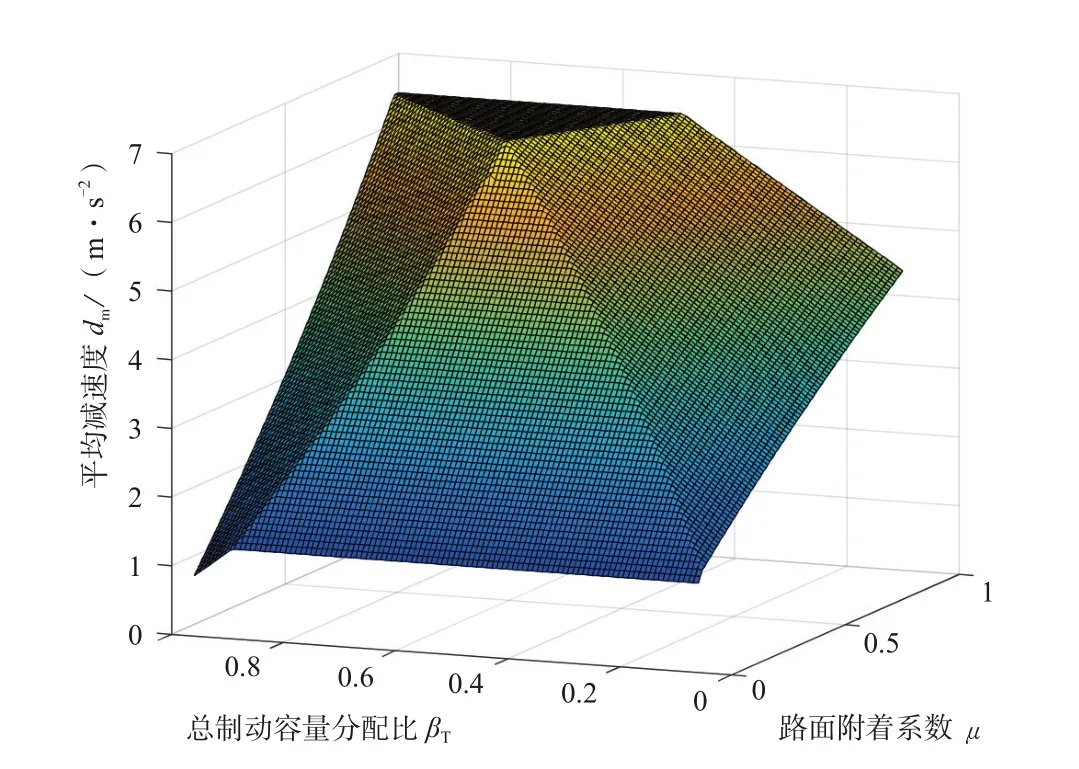
图12 平均减速度

由图12可知，平均减速度的变化规律和制动距离相互对应，因此βT的最优化取值依然是0.66。

3.3 最优化分配方法

综上所述，在所设参数模型下，汽车的总制动容量分配比取βT=0.66，也即液压制动系统前后容量按照0.85∶0.15的比例分配时，制动距离和平均减速度达到最优化，对整车的制动性最有利。当车型参数以及驱动系统容量分配改变时，均可以按照上述方法找出相应的液压制动系统最优容量分配比。

4 结论

本文对分布式驱动电动汽车驱动系统和制动系统的轴间容量分配进行了定量研究，在考虑电机再生制动能力的前提下，基于整车参数模型，采用解析法研究了驱、制动系统轴间容量分配对整车动力性参数（最大加速度、最大爬坡度和百公里加速时间）以及制动性参数（制动距离、平均减速度）的影响，并据此提出了一种轴间容量分配的优化方法，对工程应用有一定的指导意义。

（References）：

［1］ 宁国宝. 电动车轮边驱动系统的发展[J]. 上海汽车，2006（11）：2-6. NING Guobao. Development of Wheel Driving System of the Electric Vehicle[J]. Shanghai Auto，2006（11）：2-6. (in Chinese)

［2］ 余卓平，冯源，熊璐. 分布式驱动电动汽车动力学控制发展现状综述[J]. 机械工程学报， 2013，49（8）：105-114. YU Zhuoping，FENG Yuan，XIONG Lu. Review on Vehicle Dynamics Control of Distributed Drive Electric Vehicle[J]. Journal of Mechanical Engineering，2013，49（8）：105-114. (in Chinese)

［3］ 李乐. 四轮独立驱动电动车控制系统的设计[D]. 武汉：武汉理工大学，2010. LI Le. Control System Design of Four-wheel Independent Drive Electric Vehicle[D]. Wuhan：Wuhan University of Technology，2010. (in Chinese)

［4］ZHOU Y，LI S，ZHOU X，et al. The Control Strategy of Electronic Differential for EV with Four In-wheel Motors[C]// Chinese Control and Decision Conference，2010：4190-4195.

［5］ 郎文嵩. 分布式驱动电动汽车动力系统建模与驱动力控制[D].长春：吉林大学， 2013. LANG Wensong. Power System Modeling and Driving Control of Distributed Drive Electric Vehicles[D]. Changchun：Jilin University，2013. (in Chinese)

［6］ 李洋，张建伟，郭孔辉，等. 四轮驱动电动汽车轴间驱动力和制动力分配[J]. 吉林大学学报（工学版），2015，45（3）：703-710. LI Yang，ZHANG Jianwei，GUO Konghui，et al. Driving and Braking Force Distribution Between Front and Rear Axles for 4WD Electric Vehicle[J]. Journal of Jilin University（Engineering and Technology Edition），2015，45（3）：703-710. (in Chinese)

［7］ 孙晓坤. 分布式驱动电动汽车机电复合制动控制策略研究[D].北京：北京理工大学，2015. SUN Xiaokun. Study on Elctro-mechanical Braking Control Strategy for a Distributed Driving Electric Vehicle[D]. Beijing：Beijing Institute of Technology，2015. (in Chinese)

［8］EHSANI M，GAO YIMIN，EMADI A. Modern Electric，Hybrid Electric，and Fuel Cell Vehicles：Fundamentals，Theory，and Design（2nd Edition）[M]. Beijing：China Machine Press，2010.

［9］ 谷靖. 四轮驱动微型电动车整车控制[D]. 北京：清华大学，2012. GU Jing. Vehicle Control of Four-Wheel Driven Micro Electric Vehicle[D].Beijing：Tsinghua University，2012. (in Chinese)

［10］ 余志生. 汽车理论（第4版）[M]. 北京：机械工业出版社，2006. YU Zhisheng. Automobile Theory（4th Edition）[M]. Beijing：China Mechine Press，2006. (in Chinese)

［11］ 喻凡，林逸. 汽车系统动力学[M]. 北京：机械工业出版社，2005. YU Fan，LIN Yi. Dynamics of Vehicle System[M]. Beijing：China Machine Press，2005. (in Chinese)

［12］ 张元才，余卓平，张立军，等. 电动车复合制动系统相关问题分析[C]// 2007中国汽车工程学会年会论文集，2007. ZHANG Yuancai，YU Zhuoping，ZHANG Lijun，et al.Related-Problem Analysis of Electric Vehicle Hybrid Braking System[C]// Proceedings of the Annual Meeting of SAE-China，2007. (in Chinese)

作者介绍

责任作者：李濯宇（1993-），男，安徽滁州人。硕士研究生，主要研究方向为电动汽车动力系统集成与控制。

Tel：15209126508

E-mail：lzhy0512@163.com

Capacity Allocation of Driving System & Braking System for Distributed Drive Electric Vehicles

ZHANG Lijun1，2， LI Zhuoyu1，2，MENG Dejian1，2
（1. School of Automotive Studies，Tongji University，Shanghai 201804，China; 2. Collaborative Innovation Center for Intelligent New Energy Vehicle，Tongji University，Shanghai 201804，China）

Most of the existing capacity allocation methods of driving & braking systems for distributed drive electric vehicles adopt uniform distribution amongst the four wheels. Therefore, in this paper a novel capacity allocation method was proposed. The capacity allocation of driving system based on the power performance was aimed to improve the maximum acceleration and the maximum gradability and to shorten the 0-100 km/h acceleration time. The capacity allocation method of electro-hydraulic braking system based on the braking performance was aimed to reduce the braking distance and to increase the average braking deceleration. The results of theoretical analysis indicate that the proposed capacity allocation method effectively improves the power performance and braking performance of the vehicle.

electric vehicle；distributed drive；driving system；braking system；capacity allocation

U469.72

A

10.3969/j.issn.2095-1469.2017.04.04

孟德建（1982-），男，山东济宁人。博士，助理教授，主要研究方向为汽车系统动力学、振动与噪声控制。

2017-01-16 改稿日期：2017-03-29

轮毂/轮边电驱动汽车底盘系统构型与集成优化设计及综合动力学协调控制 （U1564207）

参考文献引用格式：

张立军，李濯宇，孟德建. 分布式驱动电动汽车驱制动系统容量分配方法［J］. 汽车工程学报，2017，7(4)：261-269.

ZHANG Lijun，LI Zhuoyu，MENG Dejian. Capacity Allocation of Driving System & Braking System for Distributed Drive Electric Vehicles［J］. Chinese Journal of Automotive Engineering，2017，7(4)：261-269.(in Chinese)

Tel：13482500702

E-mail：mdj0218@163.com