对2017年高考生物新课标卷Ⅰ第5题示意图的释疑

白荣宣

(浙江省温州中学 325014)

对于逻辑斯谛增长模型，中学一线教师普遍接受和采用的观点是：种群的增长率随着种群数量的增大而减小，因而对2017年高考生物新课标卷Ⅰ第5题中关于种群增长率所呈现的倒钟型曲线图的科学性产生疑惑。本文通过介绍简单逻辑斯谛增长模型和改进的逻辑斯谛增长模型中种群增长率和种群数量关系来对之释疑。

1 高考试题回顾

2017年高考生物新课标卷Ⅰ第5题：假设某草原上散养的某种家畜种群呈S型增长，该种群的增长率随种群数量的变化趋势如图(图1)所示。若要持续尽可能多地收获该种家畜，则应在种群数量合适时开始捕获，下列四个种群数量中合适的是

A．甲点对应的种群数量

B．乙点对应的种群数量

C．丙点对应的种群数量

D．丁点对应的种群数量

参考答案：D。

2 简单逻辑斯谛增长模型中的种群增长率r与种群数量N关系

在特定条件下，一个个体最大潜在生殖量叫做“内禀自然增长率”(intrinsic natural rate of increase)，实际上就是指在资源不受限制的环境中，种群增长率理论上能达到的最大值[1]。而逻辑斯谛增长(logistic growth)是指在资源有限、空间有限和受到其他生物制约条件下的种群增长方式，其增长曲线很像英文字母S，又称“S”型增长曲线。种群的逻辑斯谛增长总是会受到环境容纳量(carring capacity)K的限制，且种群数量N与种群增长率r之间存在线性关系[2]，即种群增长率随着密度上升而按比例降低，最简单的是每增加一个个体，就产生1/K的抑制影响[3]。因此，逻辑斯谛增长模型中的种群增长率r可以表示为r=rm(1-N/K)，其中rm表示种群的内禀自然增长率。即逻辑斯谛增长模型中的种群增长率r与种群数量N关系为一次函数关系(图2)，这就是简单的逻辑斯谛增长模型中种群增长率与种群数量关系，也是中学一线教师普遍采用的观点。

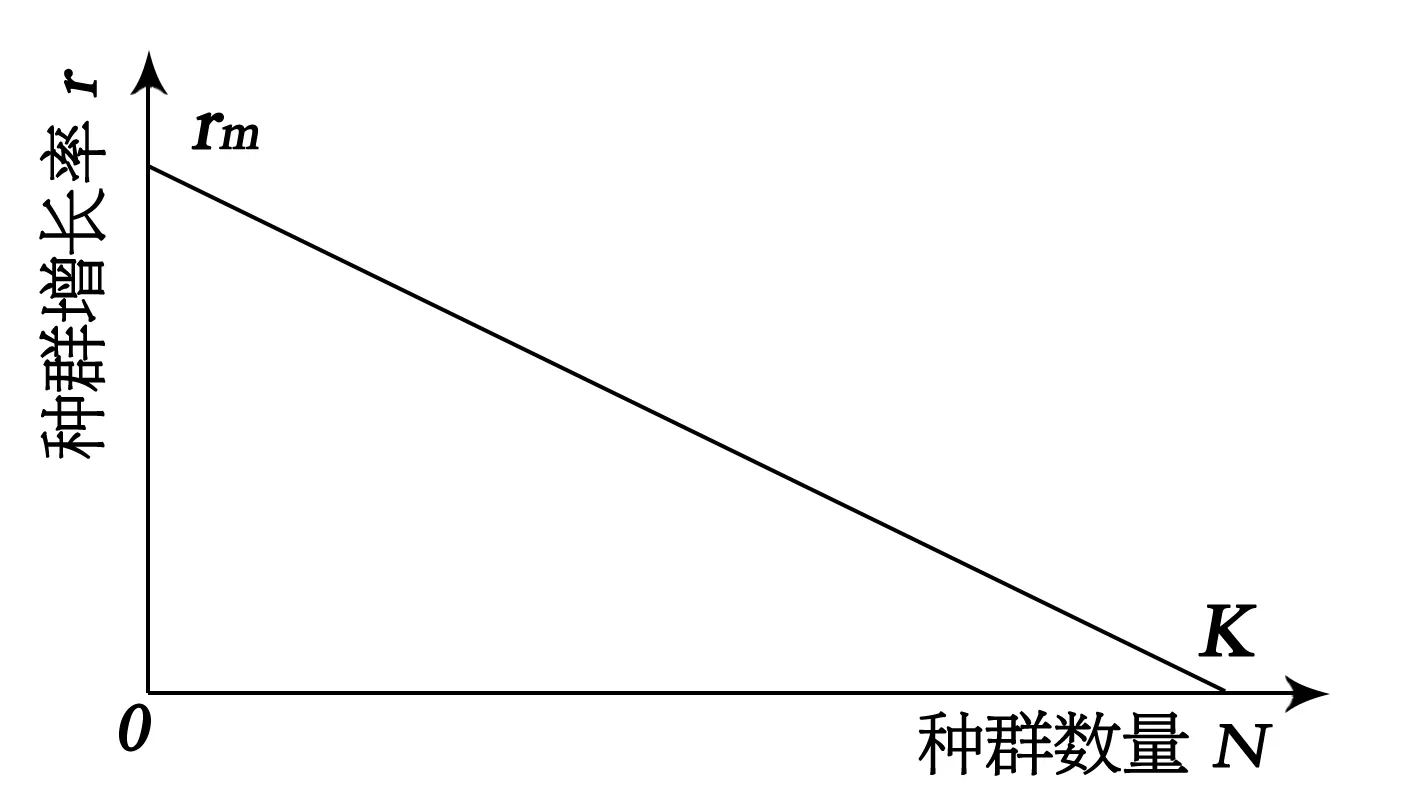
图2 简单逻辑斯谛增长模型中种群增长率r与种群数量N的关系

3 基于阿利氏效应改进的逻辑斯谛增长模型中种群增长率与种群数量关系

所谓阿利氏效应(Allee effect)，是指有些生物在种群密度很低时，其种群数量是下降的，并且会因为每个个体增长率的下降而走向灭绝的实际情况。例如，最起码的种群密度对于有效寻找配偶和逃避敌害是必不可少的，这对于那些具有一定社会结构的动物来说尤其重要[2]。本文高考题中的“家畜”应该属于这类型动物，而题干又是假设该家畜在草原上散养的情况，因此具有种群的阿利氏效应。为了改进逻辑斯谛增长模型种群增长率方程，以便把种群最低起始密度的概念包括在内，在改进的逻辑斯谛方程中增加一个系数，即把M(种群增长所必需的起始密度)引入简单逻辑斯谛方程，从而使逻辑斯谛增长模型中的种群增长率改为r=rm(1-N/K)×(1-M/N)[2]。不难看出，在该改进的逻辑斯谛方程中，当种群数量N小于种群起始密度M时，种群增长率r为负值，种群数量下降；当种群数量N大于种群起始密度M时，种群增长率r为正值，种群数量上升。而且，当种群数量N略大于种群起始密度M时，种群增长率很小，几乎等于0；当种群数量N接近环境容纳量K时，种群增长率也很小，也是几乎为0。根据改进后的逻辑斯谛方程，可绘制出种群增长率r与种群数量N之间关系图(图3)[2]。

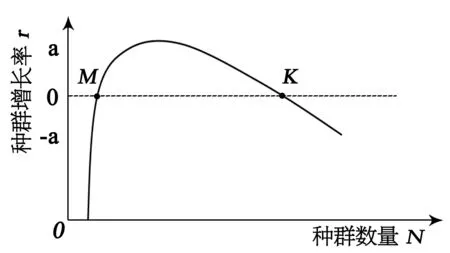
图3 改进的逻辑斯谛增长模型中种群增长率r与种数量N的关系

4 结论

本文高考题中的种群增长率和种群数量关系的倒钟型曲线图，是假设该家畜散养在草原上，并在此基础上考虑了阿利氏效应的实际情况而绘制的。只是该曲线图仅呈现了种群数量N在起始密度M和环境容纳量K之间的种群增长率和种群数量关系；另外，图中横坐标种群数量也不是从原点O开始，而是从一定数量(起始密度M)开始的。因此，该图不存在科学性问题。