变压器漏感的有限元计算

毕艳军，于敏丽，郭 臻

(1.邢台职业技术学院 电气工程系,河北 邢台 054000; 2.国网河北电力公司 邢台供电分公司,河北 邢台 054001)

变压器漏感的有限元计算

毕艳军1，于敏丽1，郭 臻2

(1.邢台职业技术学院 电气工程系,河北 邢台 054000; 2.国网河北电力公司 邢台供电分公司,河北 邢台 054001)

由于变压器漏磁场的存在，导致变压器的损耗增加，运行效率降低，出现局部过热，绕组变形等情况，甚至导致变压器绝缘损坏，对变压器安全稳定运行造成巨大的威胁。本文基于有限元法，建立了真型10 kV三相变压器二维和三维短路试验模型。依次仿真了二维、三维变压器模型得到了漏磁场、漏感结果，并将结果与现场试验测得值以及理论计算值进行对比，得出了结论：进行短路试验仿真，二维仿真模型漏感误差仅为7.6%，结果优于三维仿真模型，而二维、三维仿真模型均优于传统磁路法；通过有限元法建立的二维变压器绕组仿真模型可以准确计算电力变压器漏感。

变压器; 漏感; 电磁场; 有限元法

0 引 言

电力变压器是电力系统中最重要的电气设备之一[1-2]，作为整个电力系统的转换枢纽，其安全稳定运行是影响电力系统的安全、稳定的重要因素。随着国家经济的快速发展，各行业对电力极大需求也促使电力工业迅速发展。目前单台电力变压器的容量越来越大，电压等级也越来越高，相应的漏磁场也随之增加。漏磁场的增加，会给变压器带来杂散损耗增加、绕组变形等不良影响。据估计，磁场强度每增加20%，相关的杂散损耗将增加40%[3]。较大的杂散损耗不仅会影响经济效益，更会带来对变压器安全运行造成危害的严重问题。变压器漏感作为描述变压器漏磁场的重要参数，在变压器设计开发与保护中日益受到电力行业的重点关注。

(1) 漏磁场引起杂散损耗增加，占据了变压器负载损耗的一部分，引起变压器产生较大温升，不仅会影响变压器的传输效率，还会影响其使用寿命；而且由于变压器结构复杂，在不规则金属构件上漏磁场往往分布不均，集中在局部面积上的损耗会引起较大的过热，使得变压器绝缘遭到破坏，对电力系统安全运行带来难以估量的危害。

(2) 在大型电力变压器，低压线圈电流可达几十kA[4-5]，或是当变压器发生短路故障时，产生极大的暂态短路电流，这些大电流产生很大的漏磁场，甚至产生巨大的电磁力，使得变压器绕组变形，对变压器绝缘和机械结构造成致命的威胁。

(3) 为了减小变压器附加损耗、局部过热、绕组变形等情况，保证变压器安全稳定运行，迫切需要深入研究变压器在不同工况下的漏感特性和漏磁场分布规律，能够对变压器在设计和制造上提出更为合理和可行的方案，提高变压器的抗短路能力，具有非常重要的技术和经济意义[6-8]。

目前的计算法包括磁路法、能量法、有限元法等。传统的磁路法适合于在计算简单结构变压器的漏感，对于实际的电力变压器结构复杂，漏磁场分布也相当复杂，很难精确计算漏感，误差往往较大。能量法是利用漏磁场的能量进而计算变压器的漏感值，而计算漏磁场的能量往往需要知道变压器漏磁场的分布，而漏磁场的分布往往采用有限元法，因此能量法常常和有限元法配合使用求解变压器漏感[9-11]。

在这些计算漏感的方法中，有限元法的优势随着计算机技术的发展而逐渐凸显出来。由于计算机的引入，基于有限元等数值方法编写的各种电磁场商业化软件进入相关的研究部门、生产企业。这些商业软件有更高的准确度、可靠性、界面友好，可用于解决工程中的关键问题，对于实际解决变压器等产品的电磁场的来说，是非常有效的工具[12-14]，使用基于有限元等数值方法开发的软件分析变压器漏磁场及漏感越来越成为一种主流方法。

基于此，本文根据10 kV真型变压器参数，通过有限元仿真，依次分析了二维、三维变压器绕组模型的漏感值，并与现场实测值以及理论计算值进行对比，得到有限元法在变压器绕组仿真模拟中的方法及可行性，从而为工程中变压器绕组状态评估及监测提供一定的思路。

1 电力变压器参数

本文选取的变压器模型主要参数见表1、表2。

表1 变压器的尺寸参数

表2 变压器铭牌参数

2 传统的电力变压器漏感求解结果

2.1变压器短路试验实测

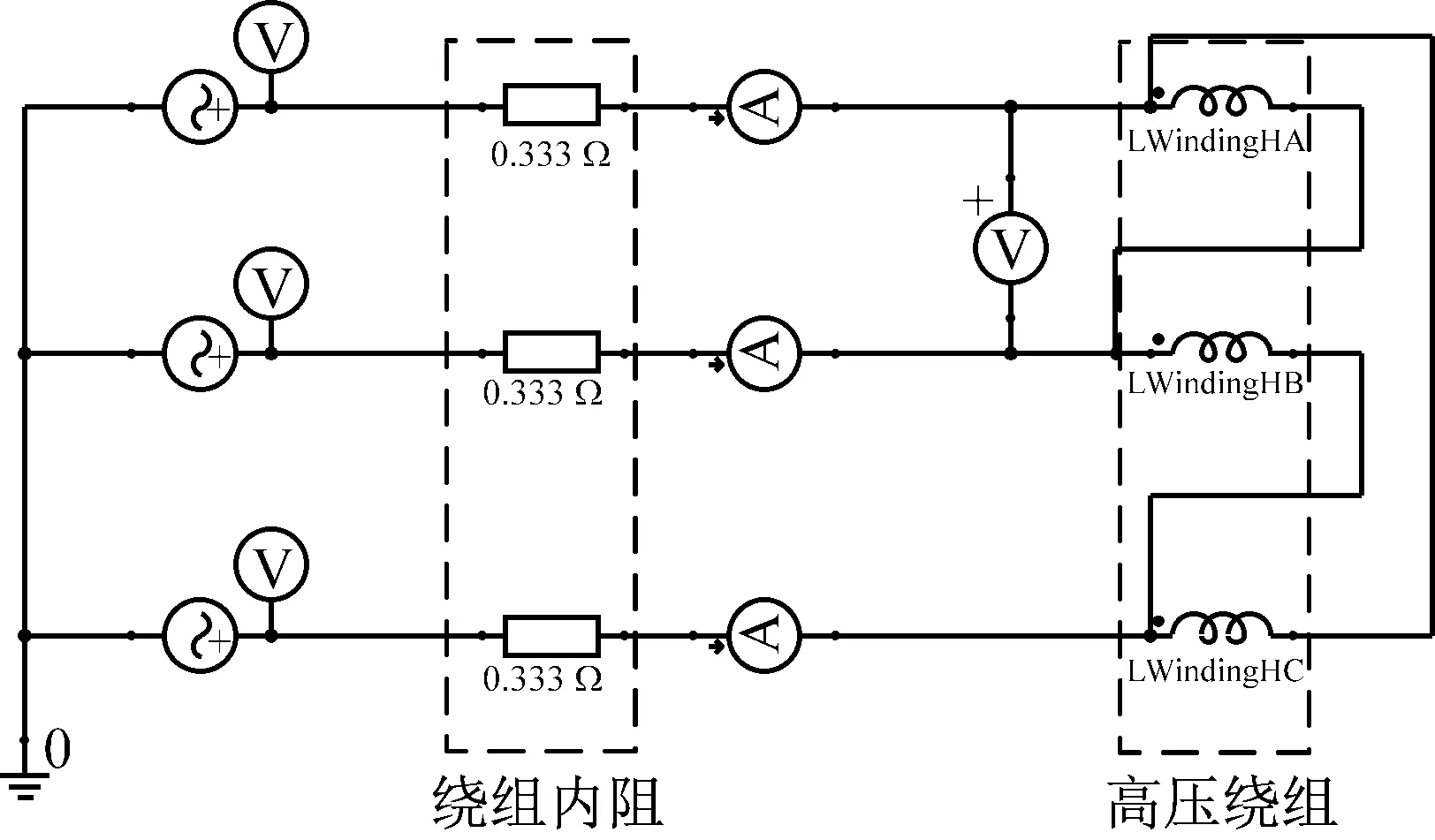
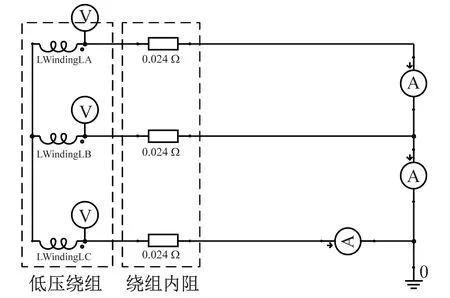
在工程中测量三相变压器的漏感，常采用变压器短路试验。变压器短路试验是指：在试验时，将二次侧绕组短路，一次侧加上可调的低电压；调节外加的低电压，使得短路电流达到额定电流，测量此时的一次电压、输入功率、和电流。即可确定漏感。变压器短路试验接线如图1所示。

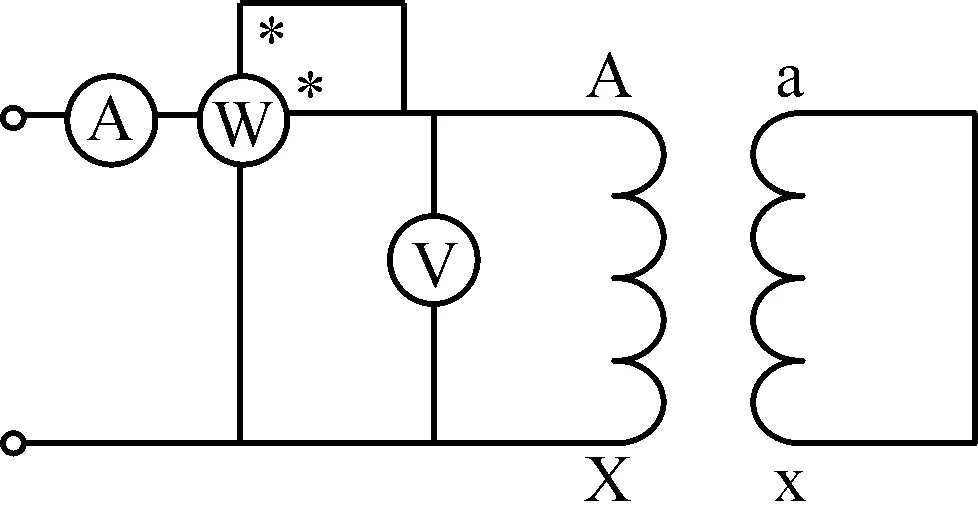
图1 短路试验的接线图

变压器漏阻抗即为短路时所变现的阻抗,即：

(1)

由于短路电压很低，此时铁芯中的铁耗很小，若不计铁耗，短路时输入功率Pk可认为全部消耗在一次和二次绕组的电阻损耗上，故短路电阻为：

(2)

则短路电抗为:

(3)

漏抗和漏感有如下关系：

Xk=ωLk=2πfLk

(4)

通过此方法得到的短路电抗为归算到一次侧时的值，得到漏感的现场测得值约为54 mH。

2.2传统磁路法计算

图2所示为变压器结构图。

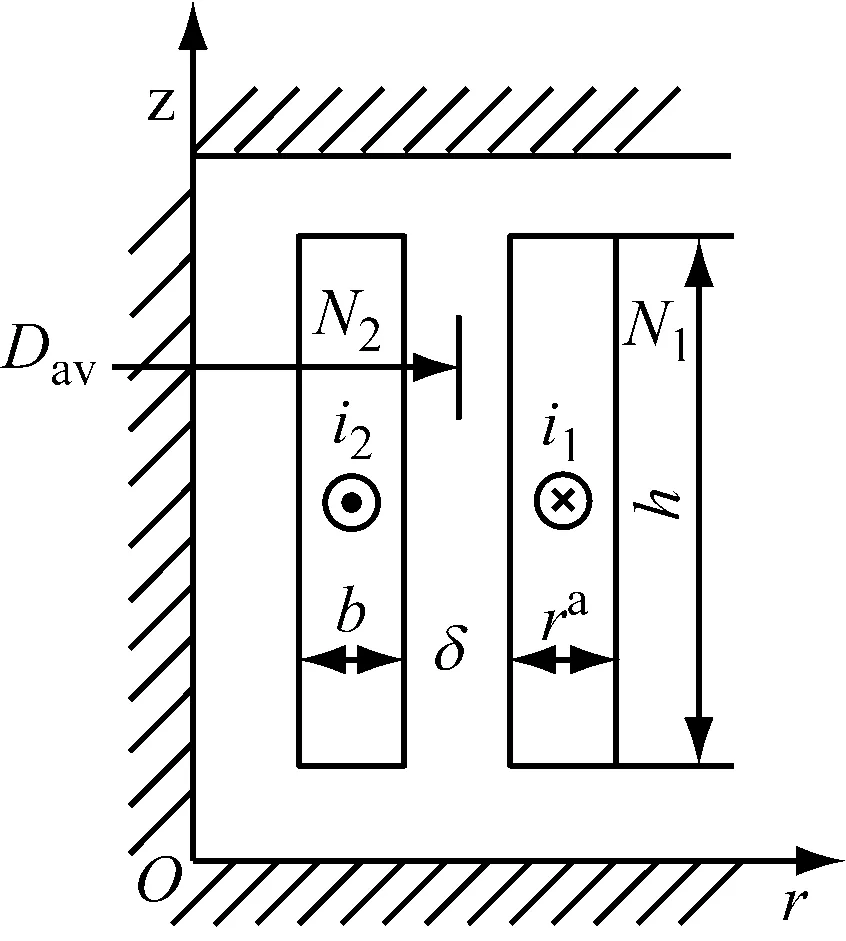
图2 变压器高低压绕组

采用磁路法，经过推导[15]可得一次和二次绕组的漏电感为：

(5)

式中：δ、h和Dav为高、低绕组的径向气隙、绕组高度和平均半径；a、b分别为高压绕组和低压绕组的径向厚度；N为绕组的匝数。通过该方法计算得到图1变压器漏感值为63.1 mH。

3 基于有限元的变压器短路试验仿真

根据表1、2参数对变压器进行建模，利用模型对仿真变压器短路试验，得到变压器的漏感。

3.1基本仿真设置

实际变压器包括上下垫块、铁心夹件、上下木楔、支撑梁等各种部件，直接按照变压器原型建模，将会导致模型过于复杂，运算压力大，求解时间长求解精度降低，因此在仿真建模中适当简化变压器结构且仍能保证求解精度要求，需要：忽略变压器支撑梁、铁心夹件、油箱等部件对漏磁场的影响；忽略线圈的集肤效应；假设电流在各绕组分区内均匀分布，忽略导线的涡流效应；高低压绕组的高度基本相同，认为安匝均匀分布，忽略线圈导线的去磁作用。

3.2变压器二维仿真

建立二维模型(见图3)，其中深蓝色的上下两部分代表上、下铁轭；中间蓝色的面域代表铁芯柱；绕组黄、绿、红从左到右依次代表变压器A，B，C三相绕组，其中外层区域代表高压绕组、内层区域代表低压绕组。变压器二维模型中包括绕组、铁芯、铁轭以及变压器绝缘油的材料电气参数见表3；铁芯B-H曲线见图4。

采用Maxwell的瞬态场求解。激励源选用外部电路。外电路与变压器联接组别，如图5、6所示。

将边界条件设置为Balloon，采用三角形剖分单元，使得结构剖分合理，减轻运算负担的同时能够保证良好的精度要求。将剖分单元设置为最大单元数为30 000。

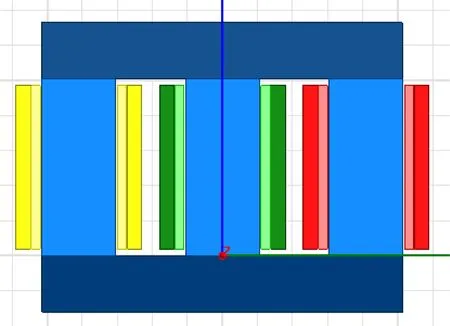
图3 变压器二维模型图

表3 变压器材料

图4 铁芯B-H曲线

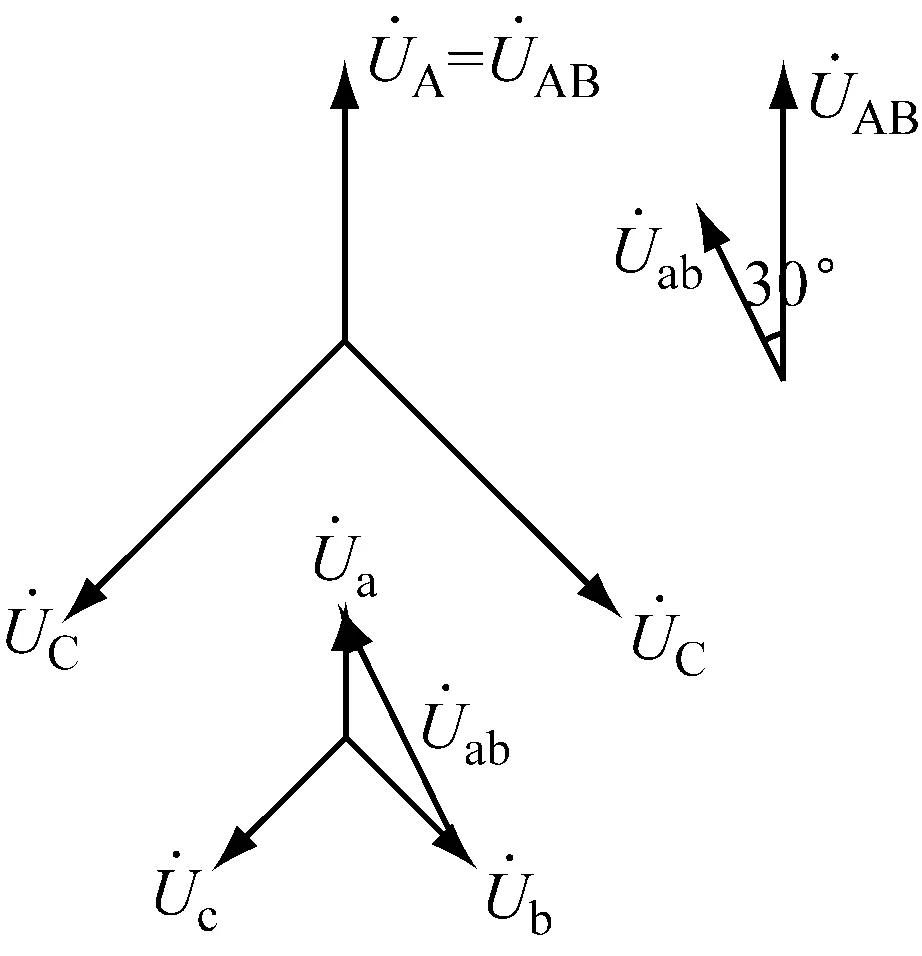
图5 Dyn11联接方式及其向量图

设置三相高压端激励为低电压，通过不断升高电压，观察电流表读数，直至电流为额定电流，此时短路试验下的变压器磁力线、磁密分布如图7、8所示。

短路试验仿真得到的结果见表4。

二维短路试验仿真漏感结果与现场测量的漏感相对误差为7.6%。此误差满足在精度范围内，由此说明二维模型的正确性，二维仿真模型能够较好的模拟实际变压器的情况。

3.3变压器三维仿真

三维模型是在二维模型的基础上建立起来的。与二维模型类似，黄、绿、红分别代表A、B、C三相绕组，灰色部件为铁轭，蓝色部件为铁芯柱(见图9)。

(a) 一次侧

(b) 二次侧

图7 短路试验变压器磁力线分布

图8 短路试验变压器磁密分布

表4 短路试验仿真结果及比较

图9 变压器三维模型

材料属性的设置和二维模型保持一致。激励源仍然采用外电路，电路形式与二维模型外电路形同，低压侧三相仍然接地短路。三维模型中的边界条件采用Zero Tangential H Field，即认为在边界外不存在磁场，所有磁场均包含在边界中。二维模型网格划分采用的是On Selection，即表面剖分。三维模型采用的是内部剖分，即Inside Selection。网格划分的结果见图10。

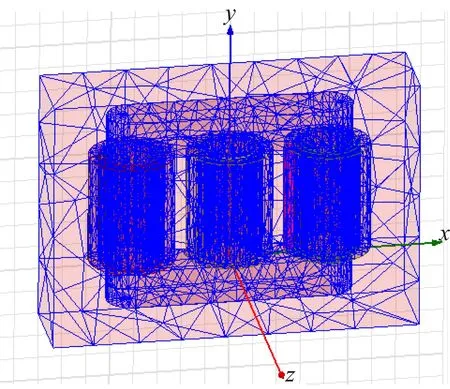
图10 三维模型三角形网格剖分

求解设置同二维模型，采用变压器短路试验的做法，高压端施加低电压，不断增加电压，观察电流波形，当电流达到稳定值时，记下此时的电压和电流。此时三维漏磁场磁密分布见图11。

图11 三维漏磁场磁密分布(t=10 ms)

根据漏磁密分布，最终得到的漏感计算结果见表5、表6。

表5 三维短路试验仿真结果及比较

表6 所有仿真模型和试验数据以及计算值对比

由表计算可得，三维仿真与现场测量的漏感值相对误差为：-12.29%。

从表6可以看出，① 传统磁路法的误差为15.7%，误差为最大；两种模型仿真的方法误差均小于传统磁路法。说明使用传统的磁路法推导出的漏感已经不能满足计算精度要求，使用软件模型仿真电磁场的方法结果更为精确，电磁场仿真法将在未来的电力行业、科研中成为一种趋势。② 二维模型的漏感结果比起三维模型更为接近实际情况。三维仿真误差较大，误差竟达到了-12.3%，其结果不能很好满足要求。相较而言，二维仿真模型结果恰能满足实验结果且运算时间不长。分析三维模型结果误差大的原因很可能是三维网格划分要求更高，其次由于三维仿真材料的属性设置不像二维采用非线性，需要假设其满足在线性区间内。考虑到三维模型仿真误差增大，求解时间长，内存占用多，因此对变压器在各种状态下，如空载、负载及短路故障时的漏感计算，均可通过建立二维有限元模型获得，并且满足了精度要求。

4 结 语

基于有限元法，使用Ansoft Maxwell软件建立了三相变压器二维和三维短路试验模型，介绍了使用Maxwell软件进行建模的操作，仿真了二维、三维变压器模型得到了漏磁场、漏感结果，并将结果与现场试验测得值以及理论计算值进行对比，得出了结论：通过有限元法建立的变压器绕组仿真模型可以准确计算漏感；变压器二维模型仿真得到的漏感值误差小，而三维仿真模型结果误差大，且运算量大；在研究变压器不同工况下的漏感特性，可以通过建立变压器绕组、铁芯的有限元法二维模型进行仿真计算。

[1] Naderi M S,Vakilian M， Blackburn T,et al．A comparison between partial discharge propagation in multiple- a and single- a transformer winding[C]∥Electrical Insulation Conference and Electrical Manufacturing Expo,IEEE，2005: 108-111.

[2] 徐 勇，周腊吾，朱英浩.变压器漏磁场分析.电力变压器手册[M].北京：机械工业出版社,2003.

[3] 石开翔.交流电机故障后电磁场的分析[D].南京：河海大学，2006.

[4] 李 朋，郝治国，张保会，等.基于有限元法的变压器漏感计算在绕组变形中的应用[J].电力自动化设备，2007，27(7): 49-53.

[5] Tsukerman I A，Konrad A，Lavers J D.A method for circuit connections in time-dependent eddy current problems[J].IEEE Trans on Magn,1992,28(2): 1299-1302.

[6] Zhang Z W， Tang W H， Ji T Y，et al．Finite-element modeling for analysis of radial deformations within transformer windings[J].IEEE Transactions on Power Delivery，2014，29(5)：2297-2305.

[7] 魏 刚，王 雪，王增平.基于ANSYS的电力变压器漏电感的计算[J].汕头大学学报(自然科学版)，2008(3): 63-68.

[8] 李文平.大型变压器的不平衡安旺对横向漏磁的影响[J].变压器，1991，28(12)，14-16.

[9] 陈玉庆.大型变压器漏磁场、电场和应力场有限元分析[D].济南：山东大学,2005.

[10] 冯 静.基于ANSYS的漏感变压器的仿真计算[D].成都：电子科技大学，2011.

[11] 朱少林，王群京.基于Ansoft的永磁同步发电机建模与仿真[J].电机技术，2008，4(2): 1-4.

[12] 耿荣林，谢德馨，李洪友.变压器箱体涡流损耗的三维有限元分析[J].变压器,2008,45(2): 1-4.

[13] Anderson O W.Transformer leakage flux program based on the finite element method[J].IEEE Transactions on Power Apparatus & System,1973,PAS-92(2): 682-689.

[14] 杨 高.基于Ansoft的电动车驱动用永磁无刷同步电动机的设计[D].重庆：重庆大学,2007.

[15] 汤蕴缪，史 乃.电机学[M]，北京: 机械工业出版社，2014.

Finite Element Method in Calculation of Power Transformer Leakage Inductance

BIYanjun1，YUMinli1，GUOZhen2

(1.Department of Electrical Engineering， Xingtai Polytechnic College,Xingtai 054000,Hebei,China;2.Xingtai Power Supply Company,State Grid Hebei Electric Power Company,Xingtai 054001,Hebei,China)

The leakage magnetic field of transformer causes increasing loss,local overheating,winding deformation,etc.,and leads to damage to the insulation of the power transformer and is a huge threat to transformer safe and stable operation.Based on the finite element method,2D and 3D simulation models of 10kV real-scale transformer are established,and the models are used to study characteristics of the leakage inductance in different conditions.The simulation results of leakage inductance are also compared between the measured value and theoretical calculation value.The results are that for short-circuit test simulation,error of 2D simulation model’s leakage inductance is only 7.6%,better than the results of 3D simulation model.Simulation models are superior to traditional magnetic circuit method,which means that finite element modeling is accurate and correct.

transformers; leakage inductance; electromagnetic field; finite element method

2016-10-15

毕艳军(1978-)，男，河北承德人，硕士，讲师，教研室主任，研究方向：电子技术与信号处理。

Tel.：15227307050；E-mail：byj978@sina.com

TP 391

：A

1006-7167(2017)07-0122-05