无源二阶GLC电路理论分析与仿真研究

刘德全

(宁夏师范学院 物理与电子信息工程学院，纳米结构及功能材料工程技术研究中心，宁夏 固原 756000)

无源二阶GLC电路理论分析与仿真研究

刘德全

(宁夏师范学院 物理与电子信息工程学院，纳米结构及功能材料工程技术研究中心，宁夏 固原 756000)

GLC电路是无源二阶电路主要结构之一，理论上多以RLC串联电路为主进行分析，而GLC电路理论分析的却很少，但由于GLC电路测试方便，而且其过阻尼状态、临界阻尼状态和欠阻尼状态3种状态过度平稳、波形易测等特点，在实验和实际应用中又非常的广泛。鉴于此，通过理论和对偶定律对GLC电路进行了分析，最后通过EDA软件对电路功能进行了仿真，采用了交互式仿真和图表仿真两种方式对电路的波形和状态轨迹波形进行了虚拟测试，仿真结果与理论分析结果相吻合，从而弥补了GLC电路在理论分析的缺失，对二阶电路的零输入响应、零状态响应和全响应有一个更深刻、全面的理解。

无源二阶电路； GLC电路； 电子设计自动化； 仿真

0 引 言

无源二阶电路是电路课程、电工课程以及相关的实验教学中研究动态电路的重要内容之一，无源二阶电路典型模型主要包括RLC串联电路和GLC并联电路，在理论教学和实验中主要以RLC电路分析为主，对GLC电路的分析甚少[1-5]。由于在工程应用中无源二阶电路应用非常广泛，黄偲等[6]研究了非线性RLC电路的新解法及数值仿真；陈国杰等[7]对RLC电路中的电感特性进行了研究；任兆香等[8]利用PSPICE软件对二阶动态电路仿真进行了设计与仿真；陈杰等[10]对方波电动势激励下的RLC串联电路共振特性进行了分析；谭志忠[10]对RLC网络进行了深入研究；孙红霞[11]利用Multisim 8平台对RLC二阶网络电路的状态轨迹进行了仿真；刘松岭等[12]对RLC二阶电路的衰减系数的估算及误差分析进行了探讨；陈军[13]利用Proteus的RLC二阶电路的数学模型进行了研究并进行了仿真分析。本文将从理论上对GLC二阶电路进行分析，利用数学模型和对偶定律对GLC电路进行分析，最后利用Proteus EDA软件对其响应及状态轨迹进行仿真分析。

1 理论分析

典型无源二阶GLC并联电路如图1所示[1,14]，所有元器件的电压与电流参考方向取关联参考方向，以电感的电流为输出观察信息号，根据基尔霍夫电流定理(KCL定理)得：

is=iR+iC+iL

(1)

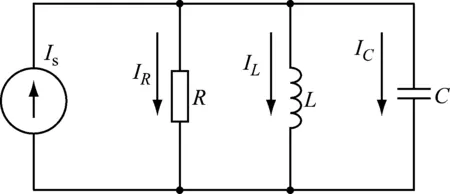
图1 GLC并联电路

由并联电路特性知，uR=uL=uC，而

代入式(1)得：

(2)

式中，is信号常取方波信号，假设电路中的储能元器件的初始储能为零，若方波信号前半周期为高电平值(IsA)，后半周期为低电平值(0 A)，则前半周恰好为GLC电路的零状态响应，后半周期为零输入响应[1,15-16]。

式(2)对应的特征方程为：

LCp2+GLp+1=0

(3)

可求得特征根为：

(4)

根据式(4)特征根的形式不同，可以产生过阻尼、临界阻尼和欠阻尼3种过程。

1.1过阻尼状态

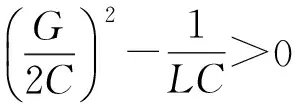
因此式(2)的通解为：

iL=A1ep1t+A2ep2t+is

(5)

由此可以得到

(6)

可以求出电路中各个元器件的电压或者电流的响应。根据is的信号值不同再分成前半周和后半周期分别讨论。

1.1.1is前半周期

前半周期is=Is，初始条件iL0+=iL0-=0，uL(0+)=uC(0+)=uC(0-)=0，电路处于零状态响应，将初始条件代入式(5)、(6)得：

(7)

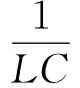
1.1.2is后半周期

(8)

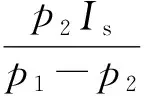
将p1p2=1/(LC)代入得

将其零状态响应uL和零输入响应uL对比，可以看出二者倒相，因此在本周内储能元器件之间互相没有能量交换，因此不能发生振荡。

1.2临界阻尼状态

式(2)的通解为：

(9)

1.2.1is前半周期

前半周期is=Is，初始条件iL0+=iL0-=0，uL(0+)=uC(0+)=uC(0-)=0，电路处于零状态，将初始条件代入式(9)得：

(10)

解得A1=-Is，A2=-δIs，结合式(9)得零状态响应：

iL=(-Is-δIst)e-δt+Is=-Is(1+δt)e-δt+Is

uR=uL=uC=L(-δIs+δIs+δIst)e-δt=LδIste-δt

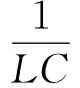
1.2.2is后半周期

A1=Is，A2=δIs

(11)

结合式(9)得零输入响应：

(12)

同理，将其零状态响应和零输入响应的uL值对比，可以看出二者倒相，按照指数函数衰减，因为在本周内储能元器件之间互相没有能量交换，所以不能发生振荡。

1.3欠阻尼状态

p1=-δ+jω=-ω0e-jβ

p2=-δ-jω=-ω0ejβ

此状态与过阻尼状态的通解相同，初始条件相同，因此前半周期：

(13)

同理可以得到后半周期：

(14)

将其零状态响应和零输入相应uL值对比，可以看出二者倒相，按照正弦函数衰减，因此在本周内储能元器件之间有能量互相交换，所以发生振荡。

2 利用对偶定理验证

由对偶定理知，R与G、L与C互为对偶元素，二阶RLC电路的3种状态是可知的[1]，利用电路中的对偶定理可以验证上述理论的推导。RLC 3种状态如下：

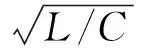
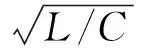
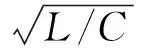
将对应的元素用对偶元素替换，得到GLC电路的3种状态：

与理论分析对比，数学模型理论分析是正确的。

3 仿真分析

3.1状态波形测试

图2 仿真原理图

(1)RV调制20%，为过阻尼状态，波形图见图3。

(2)RV调制50%，为临界阻尼状态(见图4)。

(3)RV调制80%，为过阻尼状态(见图5)。

从上图可见，过阻尼状态和临界阻尼状态是一种非振荡状态，欠阻尼是振荡状态，储能元器件电感和电容周期性的交换能量，但由于电阻对能量的消耗，故波形成衰减振荡。

3.2状态轨迹测试

任何变化的物理过程在每一时刻所处的“状态”，都可以概括地用若干被称为“状态变量”的物理量来描述。对一个n阶网络，由n个状态变量来描述。可以构成一个n维空间，每一维表示一个状态变量，构成一个“状态空间”。网络在每一时刻所处的状态可以用状态空间中一个点来表达。随着时间的变化，点的移动形成一个轨迹，称为“状态轨迹”。对电路而言，一个动态网络在不同时刻各支路电压、电流都在变化，所处的状态也都不相同。在所有UC、IC、UL、UC、IL、UR和IR6种可能的变量中，由于电容的储能为0.5CUC，电感的储能0.5LIL，故选电容的电压和电感的电流作为电路的状态变量[17-18]。了解了电路中UC和IL的变化就可以了解电路状态的变化，电路参数不同则状态轨迹也不相同。

UL过阻尼波形 (示波器仿真)

iL过阻尼波形(混合图表仿真)

UL临界阻尼波形(示波器仿真)

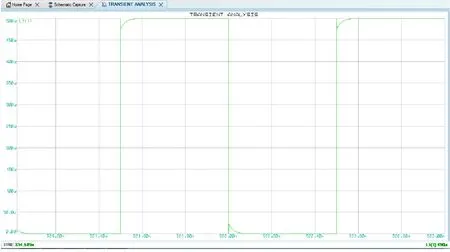
iL临界阻尼波形(混合图表仿真)

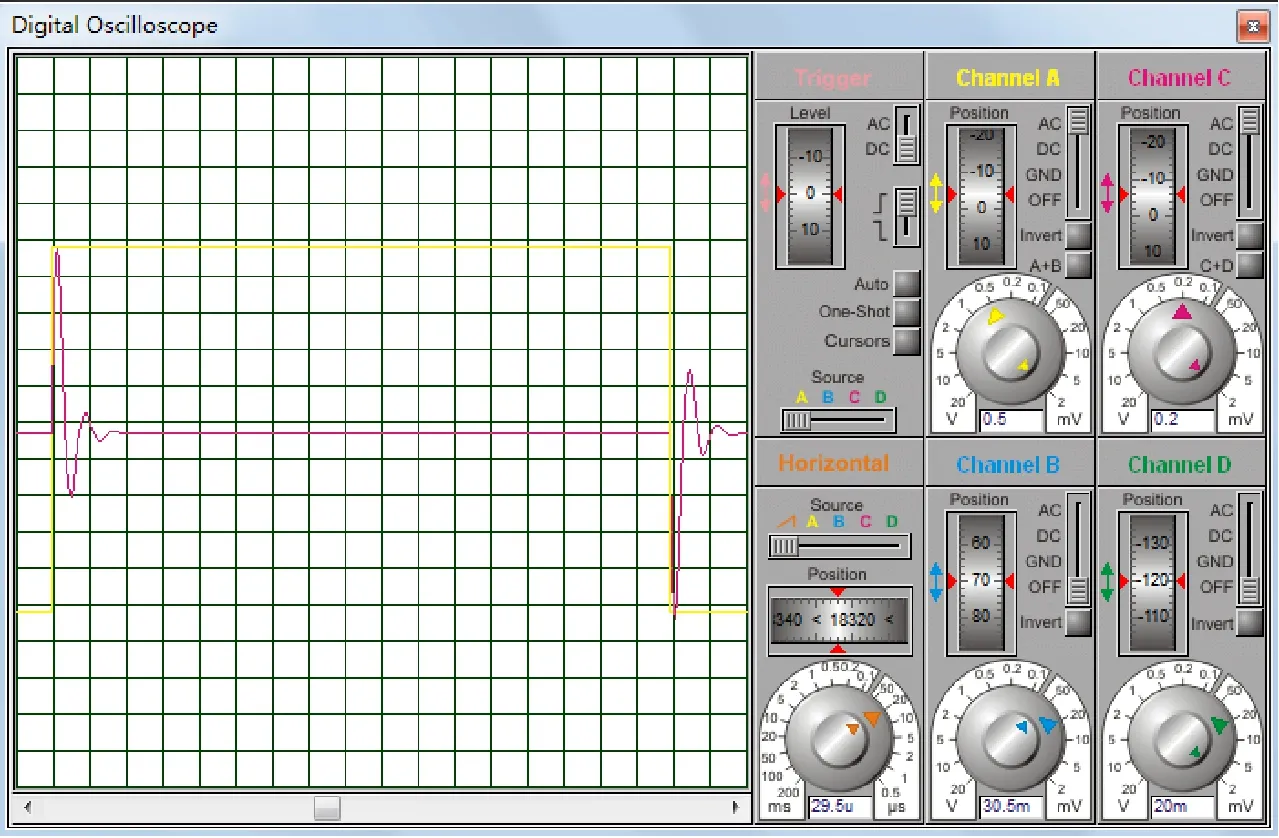
UL欠阻尼波形(示波器仿真)

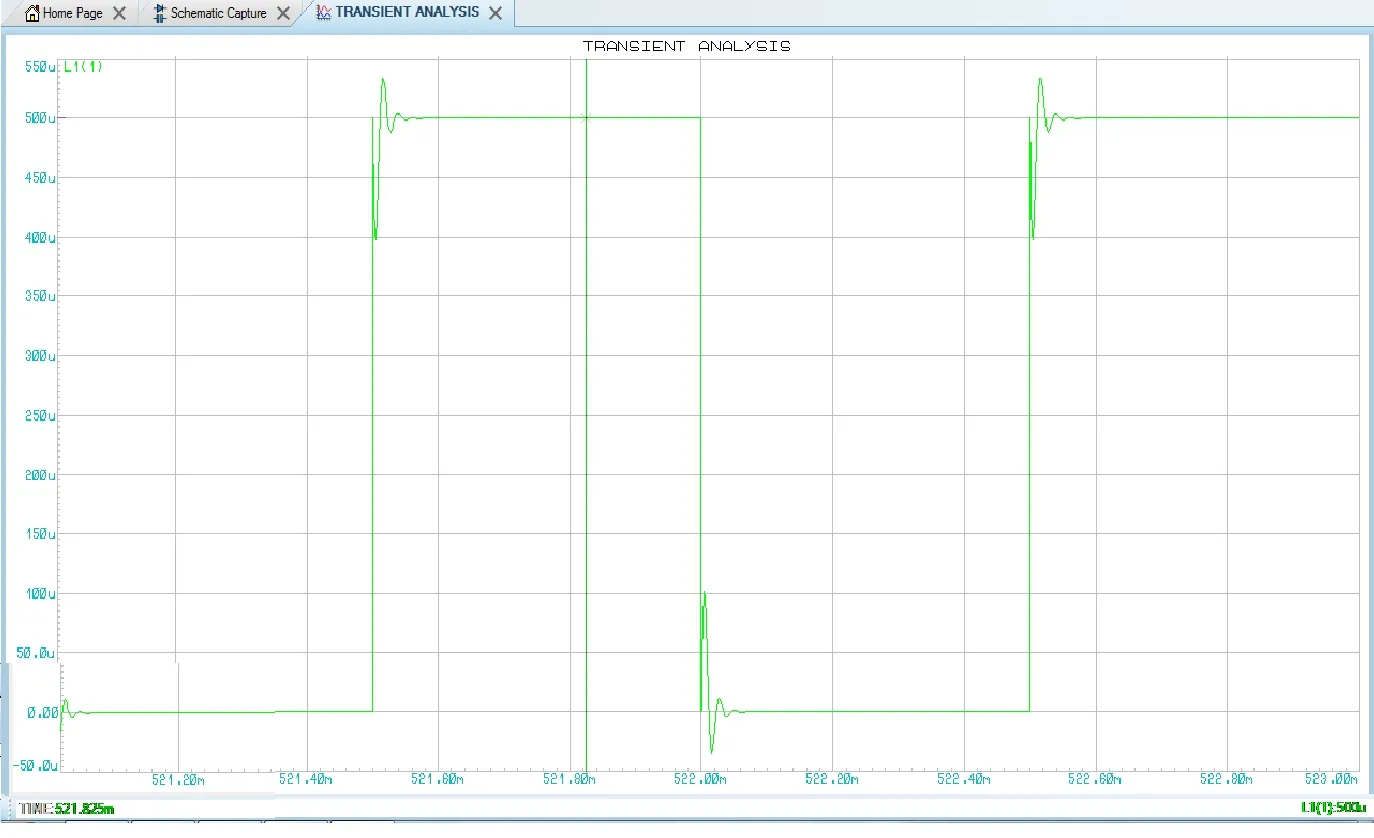
iL欠阻尼波形(混合图表仿真)

在Proteus 8.5 EDA软件中进行仿真，由于该系统提供的数字示波器只能采集电压信号，因此利用了电流控制的电压源器件将电感的电流值转换成电压值被示波器采集，状态测试电路图如图6所示。注意在示波器界面的Horizontal 面板的source项中选择B信号作为X(B信号为电感电流转换电压的值的信号)轴[14]，由于电路中的电流值很小，为了得到清晰的图像，这里将控制倍数设置为100，进行放大。测试得到状态轨迹波形如图7所示。

图6 状态轨迹测试原理图

(a) 过阻尼状态图

(b) 临界阻尼状态图

(c) 欠阻尼状态图

4 结 语

本文对GLC并联电路从理论上进行了建模分析，并利用对偶定律对其进行了验证，最后结合EDA软件，在EDA软件中进行了仿真，主要从实时波形图和状态图两方面进行了仿真，将理论分析与实际波形分析有机的结合，对GLC电路的3种状态认识更加清晰。

[1] 邱关源,罗先觉.电路 [M].北京:高等教育出版社,2008.

[2] 秦曾煌.电工学[M].北京:高等教育出版社,2009.

[3] Hambley Allan R(阿伦 R.汉布利)著.电工学原理与应用[M].熊 兰,彭光金,孙 韬，等译.北京：电子工业出版社,2014.

[4] Alexandertthew,Charles K Sadiku N O著.电路基础[M].段哲民,周 巍,李 宏等译.北京:机械工业出版社，2014.

[5] Nilsson James W(詹姆斯 W.尼尔森),Riedel Susan(苏珊A.里德尔)著.电路[M].周玉坤,冼立勤译.北京:电子工业出版社,2015.

[6] 黄 偲,余顺争．非线性RLC电路的新解法及数值仿真[J].中山大学学报(自然科学版),2016,55(3):83-88.

[7] 陈国杰,陈 奎.电感频率特性及在RLC串联谐振电路中的应用[J].大学物理,2016,35(6): 29-32,40.

[8] 任兆香,谷海清.PSPICE仿真分析与二阶动态电路教学方法研究[J].实验技术与管理，2016,33(6): 117-120,125.

[9] 陈 杰,贺泽东.方波电动势激励下的RLC串联电路共振特性研究[J].大学物理,2016,35(1):28-30.

[10] Tan Zhi-Zhong.Two-point resistance of an m×n resistor network with an arbitrary boundary and its application in RLC network[J].Chinese Physics B,2016,25(5):99-109.

[11] 孙红霞.基于Multisim 8的二阶网络状态轨迹仿真分析[J].现代电子技术,2014,37(6): 117-121.

[12] 刘松龄,熊新兵,陈首部，等.二阶电路衰减系数的估计及误差分析[J].中南民族大学学报(自然科学版),2015,34(2): 100-103.

[13] 陈 军.基于Proteus的RLC串联二阶电路的数学模型与仿真研究[J].西北师范大学学报(自然科学版),2013,49(3):51-54.

[14] 刘德全.Proteus 8-电子线路设计与仿真[M].北京:清华大学出版社,2014.

[15] 张永瑞.电路分析基础[M].西安:电子科技大学出版社,2013.

[16] 张永瑞,高建宁.电路、信号与系统[M].北京:机械工业出版社,2010.

[17] 信号与系统综合实验箱RZ8663说明书[DB/OL].http://wenku.baidu.com/link?url=WLAn7eHkx6bE88xhUhGMHg-0vLZ6iotHio9PrP3AUjpRjz_qJgByj-KepYbtaTZQ2ptrBEucd8iB5cY-NqJfOPqcBc2CsNs5odfIKpyS5PJdG.

[18] HD8662信号与系统实验讲义[DB/OL].http://www.docin.com/p-218347090.html.

Theory Analysis and Simulation Research on the Passive Second Order GLC Circuit

LIUDequan

(Engineering Research Center of Nanostructure and Functional Materials,School of Physics and Electronic Information Engineering,Ningxia Normal University,Guyuan 756000， Ningxia,China)

GLC circuit is one of the main structure of the passive second order circuit，In theory,RLC series circuit is given priority to GLC circuit,but the GLC circuit is widely used in experiments and practical situation,because its over-damped state,critically damped state and under-damped state are excessive smoothly and waveform is easy to measure.In this article,first,the GLC circuit is analyzed through mathematics and duality theorem.Second,the GLC circuit functions are simulated by EDA software and by the interactive simulation and graph-based simulation.The simulation results coincide with the theoretical analysis,the conclusions make up the GLC theoretical analysis of second order circuit zero-input response and the zero-state response and a full response,thus,one can have a more profound and comprehensive understanding for the GLC.

passive second order circuit; GLC circuit; electronics design automation; simulation

2016-10-18

宁夏教育厅高等学校科学研究项目(NGY2016200)；宁夏师范学院科研项目(NXSF1761)；宁夏师范学院本科教学工程项目(16NXSFb30)

刘德全(1977-)，男，甘肃白银人，硕士，副教授，研究领域为信号与信息处理。Tel.：13995340343；E-mail：ldqzhh@163.com

TM 133；TP 319

：A

：1006-7167(2017)07-0108-05