复平面上分形图的生成及在纺织品上的应用
王淑缓,杨旭红
(苏州大学 现代丝绸国家工程实验室,江苏 苏州 215123)
设计与产品
复平面上分形图的生成及在纺织品上的应用
王淑缓,杨旭红
(苏州大学 现代丝绸国家工程实验室,江苏 苏州 215123)
为了拓展分形图在纺织图案设计上的应用,探索纺织图案设计的快捷方法,为设计者提供更丰富、新颖的设计素材。首先,根据复平面上分形图的生成方法与程序编写,运用编程软件Visual Basic 6.0,分别研究复平面上Mandelbrot集与Julia集的生成方法,实现其可视化。然后通过改变迭代函数的形式得到一系列变化分形图,结合图像处理、平面设计软件等对得到的分形图进行纹样设计和效果模拟,利用印花技术将分形纹样应用于纺织品上。结果表明,基于分形图的纺织图案设计更加适应快捷、高效、多变的纺织生产模式。
复平面;分形;程序设计;可视化;图案设计
纺织图案设计在现代纺织品设计中占有主要地位,传统的纺织图案设计本质是依靠人脑构想来完成,通过纸、笔及绘图软件绘制而成,这种设计方法受人脑灵感的限制,并要求设计者具有专业的手绘功底,且耗时长,图案呈现过程繁琐,形成的纺织图案形式单一,局限性大。因此,分形作为一种新型的图形生成方法应运而生,分形图具有获得方法简捷,图形色彩绚丽、结构层次丰富等特点,通过函数形式变化得到的变化分形图对纺织图案设计具有一定的探究意义。
分形图是一种以数学理论作为基础,通过调整迭代函数、变化规则及颜色参数等数据进行编程设计,实现程序代码的可视化,将枯燥的数据转化为绚丽的图形或图像。由于分形图生成原理,其具有极精细结构,若没有源代码分形图将不易复制和拷贝。这种分形图实现了分形几何学与计算机图形学的完美联合,同时也是科学与艺术的融合,另外分形图的美是不可估量的,为纺织图案设计增添了新元素[1]。张聿等[2-3]运用计算机绘图方法,探究了借助电子印花技术将可视化信息展现在织物上的可行性。蔡燕燕等[4-5]对Mandelbrot集与Julia集基础分形图在图案设计上作了阐述。杨旭红等[6]对分形信息的可视化及其在纺织纹样设计中的应用作了初步探究。孙博文[1]已经对Mandelbrot集、Julia集的生成方法做了具体的说明和讨论,因此本文主要利用复平面上分形图在Visual Basic 6.0中的实现方法,通过改变迭代函数形式和参数而生成变化分形图,将其保存为图片形式。运用图像处理软件Photoshop进行二次设计,并将变化分形图广泛应用于纺织纹样设计中。
1 复平面分形图的生成原理
1.1 基本原理
复平面上的分形图主要是指基于逃逸时间算法的分形图,其原理为:令函数或映射y=f(x)作为某一变化规则,若给定初始值x=x0,则有y=f(x0),将得到的y值记作x1,则x1=f(x0),x1作为x的一个新值,则有y=f(x1),同理将得到的y值记作x2,则x2=f(x1)。对xn=f(xn-1)进行n次迭代赋值,将得到一个序列x0,x1,x2,...,xn作为x的逃逸轨迹。逃逸轨迹包括内部收敛于某一个或几个点及外部发散两个部分,在电脑屏幕上,不同的逃逸区域用不同的颜色表现出来就得到了分形图[6-7]。复平面上的分形主要包括Mandelbrot集(简称M集)和Julia集(简称J集)。
1.2 M集和J集迭代函数的变化及变化图形的生成
1.2.1 M集迭代函数的变化及变化图形的生成
M集是分形理论首创者曼德勃罗在1980年发现的,采用的是复平面上的二维迭代关系:
Z=Zm+C
(1)
式中:Z是复数变量,C是复常数量,m是幂指数。
设定初始的Z值,使C值在复平面的某个区域内有规律地变化,追踪C值得到迭代收敛的序列点,并对点进行着色绘图[8]。计算机绘图的具体操作:首先根据复数运算原理,求得展开式;再对复数的实部和虚部进行分离;最后将其转化成计算机语言,进行编程设计。
M集位于复平面中,根据计算机绘图原理及绘图步骤,Z=Zm+C的基本函数形式是m=2时,可得到如图1(a)所示分形图。

图1 M集变化分形图Fig.1 Changing fractal patterns of M set
令函数Z=Zm+C中幂指数m分别取值3,4,5,6时,生成的分形图也会随之变化,对函数进行复数运算得到如下展开式:
m=3Z= (x+iy)3=(x3-3xy2)+
(3x2y-y3)i
(2)
m=4Z= (x+iy)4=(x4-6x2y2+y4)+
(4x3y-4xy3)i
(3)
m=5Z= (x+iy)5=(x5-10x3y2+5xy4)+
(5x4y-10x2y3+y5)i
(4)
m=6Z= (x+iy)6=(x6-15x4y2+5x2y4-y6)+
(6x5y-20x3y3+6xy5)i
(5)
由此可以通过虚、实部分离,将其改写成计算机语言,进行函数替换。程序运行结果如图1(b)—(e)所示,分别为m取值3,4,5,6时的分形图。
M集位于复平面上,当函数形式为三角函数,则将迭代式Z→Zm+C中Zm替换成sinz,令Z=sinz+C,由欧拉公式[9]进行展开运算得到:

(6)
对式(6)进行虚、实部分离,转化成计算机语言:
x′=0.5×sin(x)×(exp(-y)+exp(y))+p
(7)
y′=-0.5×cos(x)×(exp(-y)-exp(y))+q
(8)
通过编程软件运行,结果如图1(f)所示。同理可知余弦展开式[9]为:

(9)
得到余弦函数分形图如图1(g)所示。
1.2.2 J集迭代函数的变化及变化图形的生成
J集的基本迭代形式与M集相同,但在Z、C取值上有所不同,在J集中,C作为某一固定值,Z作为变化点进行反复迭代,可在复平面上得到J集的图形[10-11]。J集位于复平面中,幂指数m分别取值2,3,4,5,6时会生成不同的分形图,运行结果如图2(a)—(e)所示。

图2 J集变化分形图Fig.2 Changing fractal patterns of J set
J集位于复平面上,将迭代式Z→Zm+C中Zm替换成sinz、cosz,则令Z=sinz+C,变化为三角函数形式。由欧拉公式展开,并转化成计算机语言,再通过程序设计,运行得到三角函数J集图案,如图2(f)(g)所示。
2 分形纹样设计
分形图具有一个很大的特征——自相似性,是指组成局部与整体以某种方式相似。这里提到的相似并不局限于严格的相似,它是大量统计显现出的不严格的相似,而且无论放大多少倍,始终能看到内部有与外部轮廓相似的结构,这说明分形图具有极精细结构[12]。基于分形图的精细结构,分形图在数码纺织上具有更高的实用价值。另外,可以对分形图进行二次处理,得到连续纹样并应用于数码喷墨印花技术。
纺织图案的结构形式主要包括单独纹样、适合纹样、连续纹样等。单独纹样是从分形图中直接选用整体或选取部分进行纹样设计,单独纹样在外观上并没有具体的限制,但纹样的构成形式应主次分明,次要部分起填充、烘托作用,突出主要部分[13]。适合纹样是指将整体形态限定在一定形状的范围内,呈现出某种特定的外观形态,其主要包括中心式、格律体、角隅式等[14]。纹样设计如图3所示,其中图3(a)(b)是选取图1(a)作为纹样素材,围绕中心点旋转,形成中心对称图形;图3(c)则选用图1(f)作为纹样素材,抠图、复制,使两者成90°拼接,形成角隅式纹样。适合纹样结构规则,外形美观。连续纹样是通过多次复制、往复连接,组成排列有序的图案,生活中大家看到的图案大部分是连续纹样,主要分为二方连续和四方连续两种。纹样图案如图4所示,其中图4(a)选取图1(c)(e)作为纹样素材,进行二方连续排列;图4(b)以图2(b)(c)作为基础纹样素材,通过改变颜色,进行变形组合,有花朵层叠感,形成四方连续纹样。
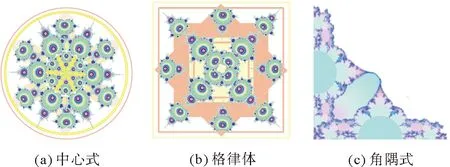
图3 适合纹样Fig.3 Suitable patterns

图4 连续纹样Fig.4 Continuous patterns
分形图在结构、色彩上都具有独特的风格,一些具有圆润的曲线构图方式,另一些具有爆破的冲击感,可以给人在视觉上带来新鲜感。所以分形图可以作为新型图案素材应用于纺织纹样设计中,具体设计实践步骤如下:根据设计风格和主体构思概念→选择相应的分形图作为素材→对选择的分形图进行图像处理→根据灵感要求进行设计→通过Photoshop软件进行实物效果演示。
2.1 设计实例1
以图1(a)的M集分形图作为素材纹样,以不同的中心点以60°旋转并复制构成中心对称的基础纹样A、B,如图5(a)所示。参照图5(b)所示,其中纹样A以5枚3飞缎纹组织排列,纹样B自然穿插其中,按排列图进行排版构成四方连续纹样的基础纹样,如图5(c)所示。拼贴成四方连续纹样,给人活泼自然、清新明快之感。
2.2 设计实例2
以图2(a)的J集分形图作为素材纹样,对素材纹样进行抠图、调色及变形处理,使其构成花朵的形态,基础纹样如图6(a)所示。参照图6(b)所示排列图进行排列设计,通过选择不同的底纹形态,产生不同的效果。
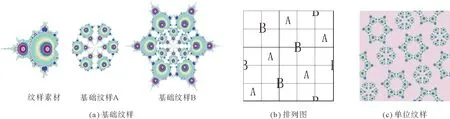
图5 M集分形图纹样设计Fig.5 Pattern design of M set fractal graph
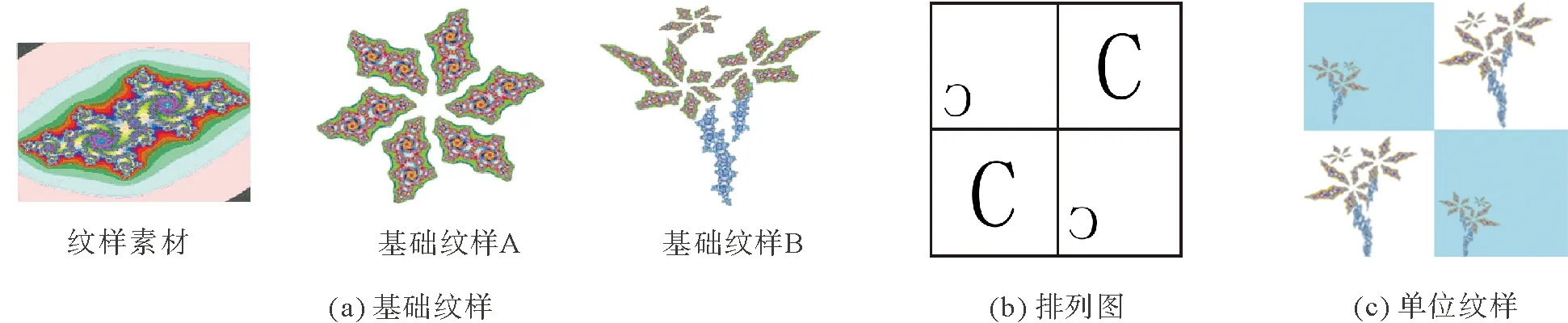
图6 J集分形图纹样设计Fig.6 Pattern design of J set fractal graph
3 分形纹样在纺织品上的应用实践
3.1 分形纹样效果模拟
根据上述设计实例中的纹样设计,利用图像处理软件Photoshop进行效果模拟。将图5(c)纹样及改变底纹颜色获得的纹样分别应用于服装、家纺产品上,效果如图7所示。将图6(c)纹样及改变底纹样式获得的纹样分别应用于服装、家纺产品上,效果如图8所示。由于分形图的显著特点是具有精细结构,原则上无论放大多少倍仍能找到与整体相似的结构。这一特点说明分形图更适用于印染在经纬纱线较细的织物上,如丝绸、高支面料等。

图7 模拟效果(设计实例1)Fig.7 Simulation effect (design example 1)

图8 模拟效果(设计实例1)Fig.8 Simulation effect (design example 2)
3.2 喷墨印花实践
选用M集分形图作为素材纹样,以图5(a)中纹样构成方法获得基础纹样,对基础纹样进行组合排列,底纹颜色进行渐变处理,获得如图9所示丝巾图案。将设计的图像数据保存为BMP文件格式,借助导带式直喷数码印花机(MS-JP5)进行印花实践,生成如图10所示丝巾成品。

图9 丝巾图案Fig.9 Silk scarf pattern

图10 丝巾成品Fig.10 Product show of silk scarf
另外,借助数码印花机,实现分形纹样在丝绸面料上的印花实践,得到如图11所示印花织物成品。

图11 印花织物照片Fig.11 Picture of printed fabric
4 结 语
1)根据复平面上分形图的生成方法,改变程序代码,从而改变分形图。分别在高次幂函数和三角函数两种函数条件下生成变化分形图,与基础分形图相比生成的分形图色彩更加丰富、层次十分突出、结构变化复杂,具有较明显的对称效果,极大程度丰富了图案设计素材库。
2)根据纺织品主题风格与应用领域要求,对分形图像进行选择和处理,借助Photoshop图像处理软件,通过旋转、复制、变形等基础操作设计得到符合要求的纹样。通过改变底纹样式和配色改变整体纹样风格,充分体现了分形纹样设计的多样性、易改变性及融合性。
3)实现复平面上分形图的设计与数码印花技术的完美结合,另外通过编程生成的数字图形具有极精细结构和自相似的特点,其适用于印染在组织结构紧密的丝绸制品上。整个过程为数字化模式,精度高、周期短、绿色环保,能引领印染行业的新方向。分形图为纺织图案设计提供了工具,为现代纺织生产模式提供了新思路,具有广阔的应用前景。
[1]孙博文.分形算法与程序设计:Visual Basic实现[M].北京:科学出版社,2004:9-159. SUN Bowen. Fractal Algorithm and Program Design to Achieve:VB [M]. Beijing:Science Press,2004:9-159.
[2]张聿,帅沁芬,付岳莹,等.基于广义Julia集的印花图案设计[J].纺织学报,2007,28(4):80-86. ZHANG Yu,SHUAI Qinfen,FU Yueying,et al. Printing pattern designing based on general Julia set[J]. Journal of Textile Research,2007,28(4):80-86.
[3]张聿,付岳莹.基于三角函数Mandelbrot集的印花图案设计初探[J].丝绸,2005(1):13-14. ZHANG Yu,FU Yueying. Studies on printing pattern design based on triangle function Mandelbrot set[J]. Journal of Silk,2005(1):13-14.
[4]蔡燕燕,宋晓霞.基于Julia集分形图形在服装图案设计中的应用[J].上海工程技术大学学报,2011,25(2):172-174. CAI Yanyan,SONG Xiaoxia. Application of fractal graphics in clothing pattern design based on Julia set[J]. Journal of Shanghai University of Engineering Science,2011,25(2):172-174.
[5]蔡燕燕,宋晓霞.基于Mandelbrot集的分形图形用于丝绸图案设计[J].丝绸,2011,48(8):35-37. CAI Yanyan,SONG Xiaoxia. Application of fractal graphs in silk pattern design based on Mandelbrot set[J]. Journal of Silk,2011,48(8):35-37.
[6]杨旭红,颜晓华.复平面上分形信息的可视化及在纺织纹样设计中的应用[J].丝绸,2007(7):39-47. YANG Xuhong,YAN Xiaohua. Visualization of complex plane fractal information and its application in textile pattern design[J]. Journal of Silk,2007(7):39-47.
[7]张菊香.逃逸时间算法生成的Julia集在纺织图案设计中的应用研究[D].苏州:苏州大学,2009. ZHANG Juxiang. Julia Sets Generated by Escape Time Algorithm Is at the Application of the Textile Pattern Design[D]. Suzhou:Soochow University,2009.
[8]陈宁,朱伟勇.M-J混沌分形图谱[M].沈阳:东北大学出版社,1998:69-79. CHEN Ning,ZHU Weiyong. M-J Chaos Fractal Images[M]. Shenyang:Northeastern University Press,1998:69-79.
[9]赵玉水.基于Mandelbrot集图形的新型面料肌理设计方法[D].杭州:浙江理工大学,2010:20-21. ZHAO Yushui. Texture Design of Fabric Based on Mandelbrot Graphics[D]. Hangzhou:Zhejiang Sci-Tech University,2010:20-21.
[10]张聿,张栋高,杨旭红,等.纺织设计中Julia集可视化信息表征方法的研究[J].苏州大学学报(工科版),2002,22(1):25-28. ZHANG Yu,ZHANG Donggao,YANG Xuhong,et al. Studies on fabric patterns designing with visual information in Julia set[J]. Journal of Soochow University (Engineering Science Edition),2002,22(1):25-28.
[11]柯福军,张方强.分形几何与分形花形的迭代函数系统方法[J].纺织学报,2003,24(5):43-44. KE Fujun,ZHANG Fangqiang. Fractional geometry and fractional patterns on overlapping function system[J]. Journal of Textile Research,2003,24(5):43-44.
[12]李杰.基于遗传算法的分形艺术图案生成方法的研究[D].济南:山东师范大学,2009. LI Jie. Research of Fractal Artistic Graphics Generation Method Based on Genetic Algorithm[D]. Ji’nan:Shandong Normal University,2009.
[13]胡晨晨.基于分形理论的服装面料图案设计及应用研究[D].杭州:浙江理工大学,2016. HU Chenchen. Fabric Pattern Design and Application Research Based on the Fractal Theory[D]. Hangzhou:Zhejiang Sci-Tech University,2016.
[14]孟广利.L-系统分形图在纺织纹样设计上的应用[D].苏州:苏州大学,2012. MENG Guangli. Application of L-system to Textile Pattern Design[D]. Suzhou:Soochow University,2012.
收稿日期:2016-12-01;修回日期:2017-06-14
基金项目:国家社科基金艺术学一般项目(16BG112);四川省教育厅人文社科一般项目(16SB0056)

Generationoffractalimageoncomplexplaneanditsapplicationintextiles
WANG Shuhuan,YANG Xuhong
(National Engineering Laboratory for Modern Silk,Soochow University,Suzhou 215123,China)
This paper aims to expand the application of fractal graph in textile pattern design,explore a convenient method of textile pattern design,and provide designers with more abundant and novel design materials. Firstly,according to the generation method and programming of fractal graph on complex plane,the method of generating Mandelbrot set and Julia set on complex plane was studied with Visual Basic 6.0,with a view to realizing visualization thereof. Secondly,a series of variation fractal graphs were obtained by changing the form of iterative function,pattern design and effect simulation of the obtained fractal graphs were conducted with image processing and graphic design software,and the fractal patterns were applied in textiles with printing technology. The results show that textile pattern design based on fractal graph is more suitable for the fast,efficient and changeable textile production mode.
complex plane; fractal; program design; visualization; pattern design
10.3969/j.issn.1001-7003.2017.08.010
2016-09-30;
:2017-06-13
江苏省高校优势学科二期建设项目(苏政办发〔2014〕37号)

TS941.26
:B
:1001-7003(2017)08-0056-06 < class="emphasis_bold">引用页码
页码:081202

