基于概率统计的水电机组状态评估数据特性研究

周 叶,潘罗平,曹登峰

(中国水利水电科学研究院,北京 100038)

基于概率统计的水电机组状态评估数据特性研究

周 叶,潘罗平,曹登峰

(中国水利水电科学研究院,北京 100038)

简要介绍了基于健康样本的水电机组状态评估方法,提出完整的健康模型分为特征数据、影响因素和健康样本3部分,然后针对特征数据的统计特性展开了分析与研究。首先对能反映机组运行状态的传感器和信号参数进行分类,再根据参数关系的复杂程度,将其分为基本特征数据和组合特征数据,并分别给出了其计算方法和特征值的选择。最后,文章通过选取电站长期运行的实际状态数据,对两种类型的特征数据进行统计分析,得到其数据特性和影响因素并给出相关结论。

水电机组;健康样本;特征数据;统计特性;状态评估

1 前言

与机组发生故障时需要及时判别和处理不同,状态检修最终的目标是指导检修计划和检修内容,以发现并消除机组潜在的故障,因此其重点在于收集并积累设备的状态信息,并对其发展趋势进行预测和评估。而当前国内外诊断技术的研究大多集中于故障的分析和识别,实际上,由于水电机组故障相对复杂,很难直接检测到具体的特定故障。因此,要想提高水电机组状态监测的实用性,切合水电厂的实际需要,需要了解机组长期运行的状态和发展趋势,最终指导设备的检修计划及内容[1]。

而随着测试技术和信息技术的不断发展提高,监测设备越来越成熟,其应用越来越广泛,各电站通过各种状态监测系统积累了机组长期海量的运行状态数据,使得大数据和统计理论在水电机组诊断检修中的研究和应用成为可能。

基于实用性和状态检修的需求,本文从概率统计学的角度研究机组长期运行的状态数据,建立机组重点或关键部位的评估模型,研究其发展趋势和变化规律,以实现机组的运行状态评估。作为基于大数据的水电机组状态评估方法研究成果,文献[2]中提出了基于健康样本的水电机组状态评估方法,按照其结构设计内容,研究思路分为数据特性、模型特性和评估方法研究3个部分,本文的研究内容为第一部分。

文章首先简单介绍了基于健康样本的水电机组运行状态评估方法,并对能反映机组状态的测量参数进行分类和计算方法分析,然后设计了两种不同的特征数据模型,最后结合模型结构通过大量的真实数据验证分析机组运行状态特征数据的统计特性。

2 基于概率统计的水电机组诊断评估方法

2.1 基于统计学的新异类检测定义

新异类检测方法(Novelty Detection Method)是一种检测隐藏在大量正常数据中的未知或异常现象的技术,它通过对已知状态观测样本的学习,实现对机器学习系统在训练时未曾遇到的、新的未知的或异常现象的识别,属于数据挖掘中的无监督学习方法[3]。

依据模型数据的统计特性,获取模型样本的分布,并判断测试样本是否属于同一分布,这种检测方法称为基于统计学的新异类检测方法。根据数据和模型的复杂程度不同,可以采用不同的统计学方法。

由于不需要先验故障知识,且主要诊断依据基于数据的统计特性,更适用于已安装且长期运行状态监测系统的水电厂。虽然这种方法在没有先验故障知识时,无法得到准确的故障分类和判别,但作为异常状态识别方法,可以在状态识别、趋势预估上起到较好的效果,并为故障诊断提供依据。

2.2 基于健康样本的水电机组状态评估方法

文献[2]中对基于概率统计的水电机组状态评估诊断方法进行了详细的描述,这里对该方法进行简单的阐述和补充。

对水电机组的运行状态进行评估,需要利用机组的历史状态测量数据,对不同测点参数建立数据模型,数据模型包括基准值和限值两部分,这里将机组在稳定运行状态下,由测点基准值和限值组成的特征数据模型称为健康样本(Health Model)。通过机组当前的实时监测值与健康样本的比对分析,得到机组的运行健康状态、劣化度和变化趋势。

在实际分析过程中,由于水电机组的状态监测参数大多与其运行条件等有关,如果统计分析时不予以考虑,会导致样本分散,标准偏差大,不利于健康样本的确定。因此,在处理样本数据时,需要将样本按多维影响因素进行划分(对机组运行工况而言,典型的如有功、水头、导叶开度等),对不同分区内的数据分别建立相应的健康样本,也可大致分为稳定区和非稳定区进行分析,进而评估机组在整个运行条件范围内的健康状态。

因此,一个完整的健康样本模型分为3部分,①该模型的特征数据,即我们选择的参数物理量以及这些物理量的特征值,它由单个或多个测点参数构成,单个参数的,如某导轴承摆度信号的峰峰值、水轮机顶盖的水压脉动主频值等,多个参数的,如最大最小瓦温差等;②影响因素,即生成模型时需要考虑的影响参数值变化的因素,二维模型指单个影响因素(如机组工作水头)与特征数据的组合,三维模型指两个影响因素(如机组有功和工作水头)与特征数据的组合;③健康样本,即该特征数据对应影响因素的运行基准值和限值。本文主要研究健康样本模型的第一部分即特征数据的结构设计及其统计特性分析。

以机组有功和水头作为主要工况限定条件为例,将机组有功、水头和当前健康标准值设定为三维模型,其阈值初始时由当前有功和水头限定范围内的监测数据统计值确定,最终建立机组异常状态评估模型:

其中Pm为有功区间,Hn为水头区间,μi为基准值,δi为均方差/标准差,Z1i为健康下限,Z2i为健康上限,对单个特征量的健康样本而言,i为有功区间划分数和水头区间划分数之积。

3 机组运行状态特征数据

3.1 状态参数分类

要开展机组运行状态评估,首先要确定能反映机组运行特征的参数,这里按照水电机组的结构组成、运行特性和常见故障类别,将机组可能发生故障的部分划分为水轮机、发电机、轴承系统、主变压器、GIS开关(含高压断路器)、调速器及辅机系统等几个部分,首先选取每个部分里有代表性的参数构造健康样本,如部分容易反映出故障特性的特征值,再随着关注度和数据特征趋势的发展,逐步扩展到更多的参数,构造更多的状态模型。这样既利于提高诊断的效率和准确性,也能够促使故障诊断研究工作分模块、分阶段开展和实施。

与故障诊断专家系统的知识分类不同,专家系统的故障分类,重点是分析具体的故障内容,并找到对应的参数,而这里的运行状态参数分类,则是将机组的大量监测参数按照重要程度和关注度的不同进行分类,并通过挑选或组合不同的状态参数,形成机组健康模型,并不依赖于专家知识库的推理。

3.2 特征数据设计

要研究水电机组运行状态的健康指标,首先需要根据特征参数划分和组合的不同,进行特征数据的统计特性分析,确定其是否体现了机组运行状态。这里根据选取参数的复杂程度,将特征数据分为基本特征数据和组合特征数据两类。

(1)基本特征数据

单一信号参数的特征数据称为基本特征数据,虽然包含是单一参数,但对该参数的特征值计算,依据其测量和存储方法的不同,仍然有不同的选择依据。

对于慢变量,通常只需观察其计量值的变化范围是否在控制界限以内,就可以基本判定其运行状态是否正常,如来自机组DCS以模拟量为主的监测量,包括导轴承瓦温、油泵油压油位等数据。其他如主变压器油中气体含量、发电机气隙监测值等,根据采样时间的不同,通常还存有波形趋势数据,对这种慢变量参数,主要采用幅域统计法选取其特征,即选用一段时间内的最大值、最小值、平均值和方差等。

对稳态工况下机组测点的特征值,概率密度函数是慢变量重要的特征值指标,主要为均值μ和方差δ2。如果数据集服从正态分布N(μ,σ2),可以采用区间(μ-3σ,μ+3σ)作为判断此次观测值是否超限的依据[4]。

对于快变量,如振动、压力脉动等参数的高采样率波形数据,除了需要观察其计量值(通常为时域幅值)变化情况外,还需要观察其频谱以及无量纲幅域参数的变化,才能比较准确的判断机组的运行状态[5]。

因此,快变量还需要采用波形特征数据进行统计分析,包括波形指标、峰值指标、脉冲指标、裕度指标和峰态指标等;对频谱成分特性,除了基本的转频、倍频谐波的幅值、频率指标外,还可采用功率谱密度函数、频率重心、均方频率、均方根频率、频率方差和频率标准差等作为统计分析对象。

(2)组合特征数据

组合特征数据是建立在基本特征数据基础上的一种数据类型,由于机组的运行特性常常由多个测点联合作用共同体现,故单一测点的统计特性往往很难有针对性的反映设备的健康状态。同时,为了抵消或排除影响因素对数据的干扰,可按实际情况建立相关不同测点的组合特征量,对组合特征量的特征值进行分析和评估。

若X1,X2,…为选取的相关测点参数,可建立如下不同特征量

其中,f1,f2,…为预先设定的函数关系,通过对组合特征量Y1,Y2,…的分析来评估设备状态。

以摆度信号为例,如果监测系统存储了其主频幅值和相位,就可以将振幅和相位随转速变化的关系比例,作为转子动平衡模型的特征参数。同样,对机组的导轴承瓦温、冷却水进出口温度等参数,可以通过比较和数学处理,得到一段时间的最大温差等特征值,即:△Tmax=tmax-tmin,以抵消环境温度对其数值的影响。

4 机组运行状态数据统计特性

4.1 基本特征数据的统计特性分析

(1)长期基本特征数据的分布特性

为研究长期监测数据的统计特性与分布规律,这里选取某电站15F机组2011年8月18日～2014年8月18日期间的监测数据,包括机组有功、上导Y向摆度峰峰值、上机架Y向水平振动峰峰值3个测点信号。按每2 min取特征值的均值,得到3年时间区间内的样本数据。

考虑到运行工况的影响,选取各测点在机组稳态运行时的历史数据做频率分布统计,在95%置信水平下,用Matlab的Jbtest函数进行正态分布检验,得到检验结果见表1。

表1 正态分布检验结果(2011.8.18～2014.8.18)

其数据分布直方图见图1。

图1 上导摆度和上机架振动的数据分布直方图

通过JBTest函数计算结果和数据分布直方图可以看出,两个测点数据均无法通过正态分布检验,其检验量Jbstat远远超过临界值CV。究其原因,由于选取了3年时长的机组运行数据,期间机组检修的影响和机组状态的变化较大,因此很难把3年时间的机组运行数据统一为一个标准的稳态数据模型。

(2)不同时间长度对统计特性的影响

分别以半年、3个月、1个月、1周为时间段,选取4个时间区间内的上机架Y向水平振动峰峰值数据进行正态分布检验,其概率值检验图如图2、图3所示。

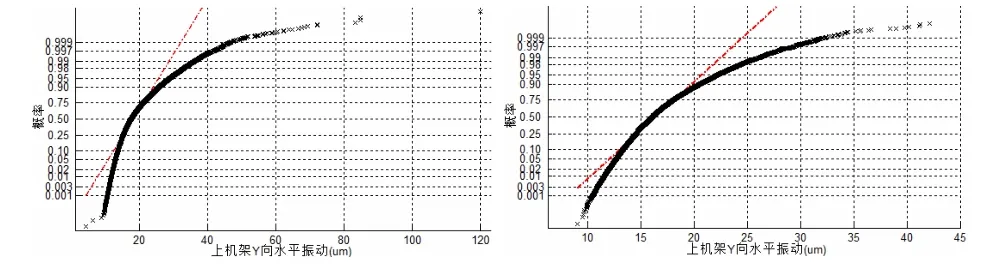
图2 15F机组上机架Y向水平振动概率值检验图(左图:半年;右图:3个月)

图3 15F机组上机架Y向水平振动概率值检验图(左图:1个月;右图:1周)

从图2、图3可以看出,随着数据时长的改变,上机架Y向水平振动峰峰值的分布特性虽然无法通过正态分布检验,但已经在逐步趋向标准正态分布。

4.2 组合特征的统计特性分析

为了消除基本特征数据受到工况和坏境因素的影响,采用组合特征的方式来进行统计分析,这里选取某电厂18F机组2014年8月31日12:00～2014年09月14日00:00:00期间的水导瓦温监测数据,期间机组满负荷运行,包括3号、4号两块水导轴瓦的瓦温数据。计算其平均值和最大瓦温差的统计特性,即在95%置信水平下,用Matlab的Jbtest函数进行正态分布检验。检验结果见表2。

表2 水导瓦温组合特征量正态分布检验结果

检验结果表明,3号水导瓦和4号水导瓦该段数据均无法通过正态分布检验,但组合测点最大瓦温差该段数据可以通过正态分布检验,认为其服从正态分布。

频率分布直方图与概率值检验图如图4所示。

图4 18F机组水导瓦温-最大瓦温差频率分布直方图和概率密度检验图

5 结论

通过对实际数据的分析和检验,可以得出如下结论:

(1)数据长度不宜选择过长。虽然概率统计方法希望取得的数据样本数越大越好,但实际验证分析证明,影响机组运行状态变化的因素很多,想要确定机组的健康样本,需要机组运行状态相对稳定,因此建议在采用率尽可能高的情况下,选取适当时长的数据进行统计分析。

(2)组合特征量相比单个特征量更容易反映机组运行特性。本文仅给出了简单的瓦温差作为示例,其他如机组发电机能量损耗、动不平衡时机架振动主频分量与转速平方比值等其他与机组运行特性紧密相关的组合特征,都可以用来进行统计分析,也容易起到较好的评估效果。

(3)通过概率统计分析可以得到机组的稳定运行状态和样本,能够作为后期机组异常状态评估和趋势预估的标准。当然,可以根据参数值的数学特性,选用其他的分布函数进行验证和分析。要想得到理想的机组健康样本,还需要考虑其基本的影响因素即工况参数的影响,可以通过网格划分得到多维特征数据,以更好的获取其统计特性。

[1]陈国庆,程 建,李友平,等.水电机组状态检修技术的几点认识[J].水电自动化与大坝监测,2012,36(4):31-33.

[2]周 叶,潘罗平,曹登峰.基于新异类检测的水电机组诊断评估方法研究 [C]//水电设备的研究与实践—第20次中国水电设备学术讨论会论文集.北京:中国水利水电出版社,2015:344-351.

[3]Markou M,Singh S,Novelty Detection:A Review–Part 1: Statistical Approaches[J].Signd Processing,2003(12).

[4]Manson G,Pierce G,Worden K,et al.Long-term Stability of Normal Condition Data for Novelty Detection[C]//Proceedingsofthe 7th International Symposium on Smart Structures and Materials,California,USA,2000.

[5]梁武科,张彦宁,罗 兴.水电机组故障诊断系统信号特征的提取[J].大电机技术,2003,35(4):53-56.

TV738

A

1672-5387(2017)07-0022-04

10.13599/j.cnki.11-5130.2017.07.006

2017-04-27

周 叶(1980-),男,高级工程师,从事水电机组状态监测与故障诊断研究工作。