反应堆压力容器用SA508Gr.4N钢的热变形行为

杨志强，刘正东，何西扣，刘 宁,2

(1 钢铁研究总院 特殊钢研究所，北京 100081； 2 昆明理工大学 材料科学与工程学院，昆明 650093)

反应堆压力容器用SA508Gr.4N钢的热变形行为

杨志强1，刘正东1，何西扣1，刘 宁1,2

(1 钢铁研究总院 特殊钢研究所，北京 100081； 2 昆明理工大学 材料科学与工程学院，昆明 650093)

利用Gleeble-1500D热模拟试验机，在温度为1050～1250℃、应变速率为0.001～0.1s-1、真应变量0.16的条件下，研究和分析SA508Gr.4N钢高温塑性变形及动态再结晶行为。结果表明：SA508Gr.4N钢的高温真应力-应变曲线主要以动态再结晶为特征，峰值应力随变形温度的降低或应变速率的升高而增加，属于温度和应变速率敏感材料；在真应力-应变曲线的基础上，建立材料热变形本构方程，较好地表征了材料高温流变特征，其热激活能为383.862kJ/mol；其硬化率-应力(θ-σ)曲线均呈现拐点且-dθ/dσ-σ曲线出现极小值；临界应变随应变速率的增大与变形温度的降低而增加，且临界应变(εc)与峰值应变(εp)之间具有一定相关性，即εc/εp=0.517；临界应变与Z参数之间的函数关系为εc=8.57×10-4Z0.148。

SA508Gr.4N钢；热变形；本构方程；动态再结晶；临界应变

反应堆压力容器是核电站核岛中的关键部件，是核电站冷却剂压力边界屏障中的一个重要设备，是核一级安全设备。压力容器起到用来装载及支撑反应堆堆芯，密封核反应产生的高温、高压冷却剂等作用。随着工业社会的发展导致对电力的需求不断增长，对于核电这种清洁能源而言，提高电力供应的一个有效措施就是提高反应堆的单堆容量，而单堆容量的增加将会导致反应堆压力容器的大型化。如AP1000型反应堆压力容器的尺寸已达到高12.2m，容器内径4.4m，壁厚225mm，总质量约425.3t[1,2]。目前广泛采用SA508Gr.3钢锻件来制造反应堆压力容器，但SA508Gr.3钢也面临着诸多问题，如强度低，韧性、淬透性差以及辐照脆化等问题[3-6]；因此，研制下一代反应堆压力容器用钢已十分紧迫。

SA508Gr. 4N钢是ASME规范中核电机组关键材料的4N级，其抗拉强度大于725MPa，明显高于其规范中的第3级SA508Gr.3钢，被认为是下一代反应堆压力容器的首选材料，如超临界水冷堆，已将该钢列为候选材料[7]。目前国内外学者针对SA508Gr.4N钢的研究主要集中在筛选合金成分，优化热处理工艺等方面。李昌义等[8]通过改变淬火冷却速率，确定不同淬火组织的含量，再结合模拟软件等效确定了SA508Gr.4N钢的淬透极限尺寸为1200mm，远超SA508Gr.3钢700mm的淬透极限。Park等[9,10]采用热力学计算，通过调节Ni，Cr和Mo等合金元素的含量，确定了不同成分、不同温度时的析出相，从而优化合金成分和热处理工艺，并调整Ni含量进行了相关验证实验，确定了不同Ni含量时的马氏体与贝氏体的含量，证明了Ni能够提高SA508Gr.4N钢的淬透性。Kim等[11]对比研究了SA508Gr.3与SA508Gr.4N钢的韧性，通过精细化表征，指出SA508Gr.4N钢具有良好韧性的原因。但关于SA508Gr.4N钢的热加工性能至今少有报道。

本工作依据反应堆压力容器锻造过程中变形温度高、变形速率低、变形量小的特点，利用Gleeble-1500D热模拟试验机对SA508Gr.4N钢进行了高温单道次压缩实验，获得了该材料不同条件下的真应力-应变数据，建立了SA508Gr.4N钢的高温本构方程，并对所得真应力-应变原始数据求解加工硬化率；同时采用硬化率-应力(θ-σ)曲线上的拐点判据及-dθ/dσ-σ曲线上的最小值，研究了该钢的动态再结晶(Dynamic Recrystallization,DRX)临界条件。

1 实验材料与方法

参考ASME国际规范的SA508/SA-508M，采用100kg真空感应炉冶炼实验钢，SA508Gr.4N钢的化学成分见表1。钢锭开始锻造的温度在1150℃左右，终锻温度在900℃左右，横向锻打，锻造成φ16mm的棒材。锻造后经650℃/2h退火后空冷。

表1 SA508Gr.4N钢化学成分(质量分数/%)Table 1 Chemical compositions of SA508Gr.4N steel (mass fraction/%)

热压缩试样尺寸为φ8mm×15mm，由退火态φ16mm的锻棒线切割而成，利用Gleeble-1500D热模拟试验机对试样进行单次轴向压缩，实验开始前在试样两端均匀涂敷润滑剂(70%石墨+25%机油+5%硝酸三甲苯酯，质量分数)，以减小其与压头之间的摩擦。试样以20℃/s速率升温到1250℃，保温300s，以5℃/s速率冷却到预设温度保温60s后开始压缩。变形温度分别为1050，1150，1250℃，应变速率分别为0.001，0.01，0.1s-1，真应变量为0.16。变形后立即水淬，保留热变形组织便于观察分析。

2 结果与分析

2.1 真应力-真应变曲线

图1为SA508Gr. 4N钢在不同温度与不同应变速率下的真应力-真应变曲线。表2为不同温度与应变速率条件下的峰值应力。

由图1可知，SA508Gr. 4N钢具有明显的稳态流变特征：在最初应变时，随应变量的增加真应力呈现直线型快速增加；真应变达到一定阶段后，真应力缓慢增大到峰值应力；真应力达到峰值后随应变量的增大，真应力缓慢下降；在应变速率为0.001s-1时随真应变的增大，真应力出现稳态阶段。真应力随真应变的宏观变化在微观上对应的变化为：变形初始阶段随着变形量的增加，位错密度急剧增加，位错间的交互作用增强，导致位错运动阻力迅速增大，表现出加工硬化。随后位错交互应力场引起的畸变能增加到一定程度时，热压缩变形中的储存能转变为再结晶驱动力，发生动态再结晶软化，因而在宏观上表现出应力增加缓慢；真应变再增加时，动态再结晶的软化作用将占据主导地位，材料的真应力逐渐降低[12]。在应变速率为0.1s-1时，由于应变速率大、变形量略小，导致在真应力-真应变曲线上未明显出现稳态流变阶段。

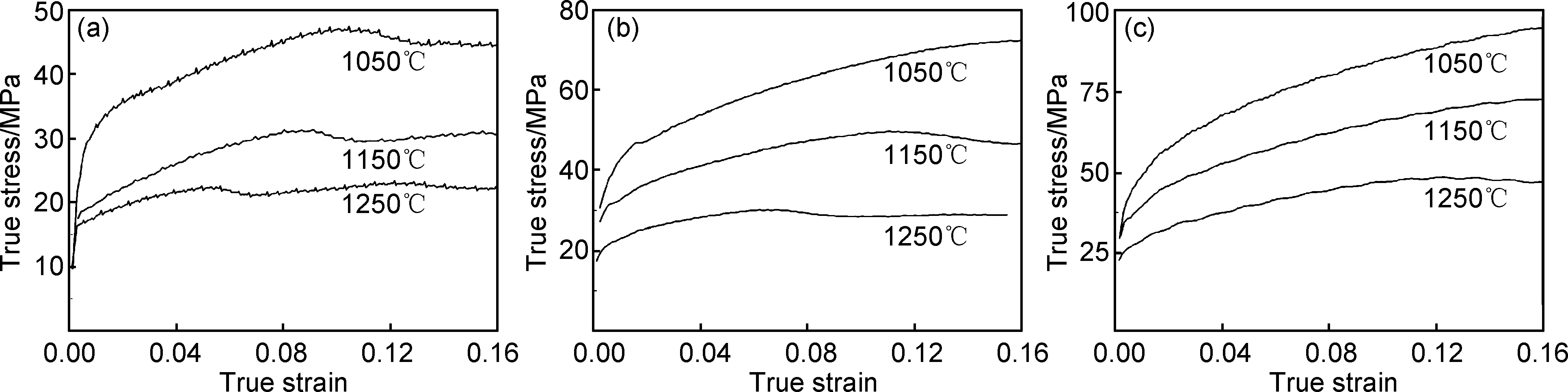
图1 SA508Gr.4N钢热变形真应力-真应变曲线Fig.1 True stress-true strain curves of SA508Gr.4N steel during hot compression deformation

Strainrate/s-1Peakflowstress/MPa1050℃1150℃1250℃0.00147.8231.5223.190.0172.7150.7930.220.1-74.5848.65

从图1中还可以看出，在恒定的速率下，流变应力随着温度的升高而降低。这是由于随着温度升高，材料动态再结晶的形核率和长大速率都提高，从而软化作用增强；而且温度越高、原子动能越大，原子间的结合力就弱，即剪切应力降低[13]。可见，SA508Gr.4N钢是温度敏感材料。

由表2可见，在恒定温度下，流变应力随应变速率的降低而减小。因为在恒定温度下、应变速率较低时，达到指定变形量所消耗的时间较长，将留给再结晶形核的时间延长，再结晶形核数量增多，再结晶软化的作用强于加工硬化。随着应变速率增加，导致热变形时间短，位错的滑移与攀移所产生的动态回复有限，晶粒内的位错密度依然保持较高水平，使加工硬化作用明显强于再结晶软化，表现为流变应力迅速升高[14]。可见，SA508Gr.4N钢对应变速率具有正的敏感性：温度越高、应变速率越小，钢变形抗力就越小，越易达到稳态变形。

2.2 变形条件对显微组织的影响

图2为SA508Gr.4N钢退火态和变形前的显微组织。由图2(a)可知，退火态锻棒的晶粒尺寸较细小，经过统计晶粒直径为9.4μm，晶粒度为10.5级。图2(b)为以20℃/s速率升温到1250℃而后保温300s的显微组织，可以看出晶粒边界清晰，晶粒尺寸较均匀，经统计晶粒直径为75.5μm，晶粒度为4.5级。可见经过变形前高温均匀化后晶粒尺寸明显增大。

图2 SA508Gr.4N钢变形前显微组织 (a)退火态；(b)热变形前Fig.2 Microstructures of SA508Gr.4N steel before deformation(a)annealed；(b)before hot deformation

变形温度1050℃时，不同应变速率热变形后的显微组织如图3所示。可以看出，3种应变速率下均发生了动态再结晶，如图3(b)，(c)箭头所示，且随变形速率的升高，动态再结晶后的晶粒尺寸逐渐减小，晶粒逐渐得到细化。应变速率较低时(0.001s-1)，晶粒尺寸较粗大，但较均匀(图3(a))。应变速率较高时(0.1s-1)，再结晶后晶粒尺寸存在较大差异呈现混晶形貌(图3(c))。

图3 变形温度1050℃时不同应变速率热变形后SA508Gr.4N钢显微组织 (a)0.001s-1;(b)0.01s-1;(c)0.1s-1Fig.3 Microstructures of SA508Gr.4N steel after hot deformation at 1050℃ at different strain rates (a)0.001s-1;(b)0.01s-1;(c)0.1s-1

应变速率0.1s-1时，变形温度为1150℃和1250℃热变形后的显微组织如图4所示。将图3(c)与图4对比可知：随变形温度的增加，动态再结晶后的细小晶粒开始长大。当温度为1250℃(图4(b))时，变化后的晶粒尺寸已达到4.5级，并已恢复到变形前的晶粒尺寸且晶粒大小不均匀。

图4 应变速率0.1s-1时，不同变形温度热变形后SA508Gr.4N钢显微组织 (a)1150℃;(b)1250℃Fig.4 Microstructures of SA508Gr.4N steel after hot deformation at different temperatures in the strain rate of 0.1s-1(a)1150℃;(b)1250℃

2.3 本构方程的建立

金属材料的高温塑性变形过程和高温蠕变过程类似，均存在热激活的过程，流变应力取决于应变速率和变形温度，在不同的应力水平下可以用双曲正弦方程来描述[15]：

(1)

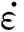
Z=A[sinh(ασ)]n

(2)

对式(2)两边取对数，可得：

lnZ=lnA+nln[sinh(ασ)]

(3)

由式(1)对1/T求偏导得：

(4)

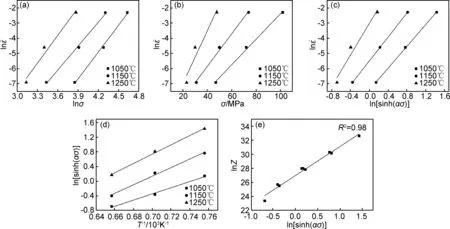
图5 峰值应力、变形温度和应变速率之间的关系；；；(d)ln[sinh(ασ)]-1000/T；(e)ln[sinh(ασ)]-lnZFig.5 Relationship between peak stress, deformation temperature and strain rate ；；；(d)ln[sinh(ασ)]-1000/T；(e)ln[sinh(ασ)]-lnZ

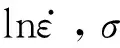
(5)

2.4 加工硬化率-流变应力曲线

一般情况下，真应力-真应变曲线是材料变形时微观组织的外在表现，真应力-真应变曲线出现峰值预示着材料微观组织发生了动态再结晶。但是通过真应力-真应变曲线并不能直接确定材料何时、何种变形程度开始发生动态再结晶，因此需要对真应力-真应变曲线进行处理，以求得材料热变形中的加工硬化率。材料的加工硬化率(θ=∂σ/∂ε)是表征流变应力随应变量变化的关系。Poliak和Jonas[18]认为材料发生动态再结晶时，其θ-σ曲线出现拐点，即利用-dθ/dσ=0的判据来确定相对应临界应力σc及临界应变εc。对热模拟实验数据进行计算可以得到不同变形条件下的θ-σ曲线和-dθ/dσ-σ曲线，如图6与图7所示。结合图6中的拐点和图7中的极小值可以确定临界应力(σc)、峰值应力(σp)、临界应变(εc)和峰值应变(εp)。临界应变与峰值应变及其比值见表3。

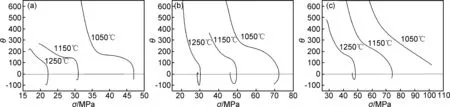
图6 不同变形条件下SA508Gr.4N钢的θ-σ曲线；Fig.6 θ-σ curves of SA508Gr.4N steel under different deformation conditions

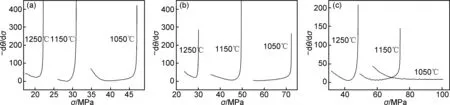
图7 不同变形条件下SA508Gr.4N钢的-dθ/dσ-σ曲线；Fig.7 -dθ/dσ-σ curves of SA508Gr.4N steel under different deformation conditions

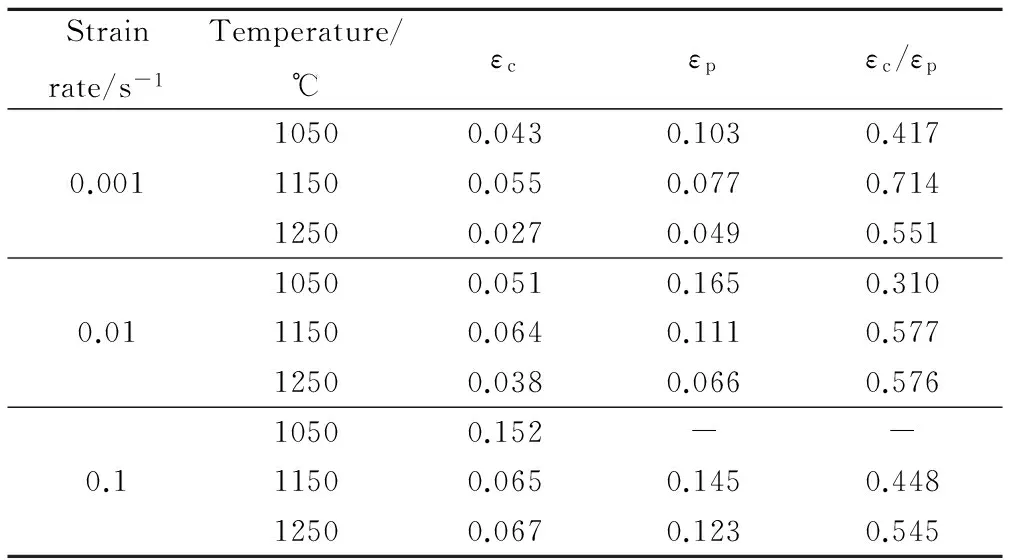
Strainrate/s-1Temperature/℃εcεpεc/εp10500.0430.1030.4170.00111500.0550.0770.71412500.0270.0490.55110500.0510.1650.3100.0111500.0640.1110.57712500.0380.0660.57610500.152--0.111500.0650.1450.44812500.0670.1230.545

由图6可知，SA508Gr.4N钢的θ-σ曲线在各个温度和应变速率均出现拐点。如图6(a)所示，当应变速率为0.001s-1时，各应变温度的θ-σ曲线均明显出现拐点，拐点处所对应的应力值就是临界应力。加工硬化率(θ)第1次等于0时对应的应力即为峰值应力(σp)，第2次等于0时所对应的应力为稳态应力(σs)。图6中只有变形温度为1050℃、应变速率为0.1s-1时，θ-σ曲线θ始终大于0，这表明在这一变形条件下无峰值应力，但曲线上亦有拐点。为了更加精确曲线中拐点位置对θ-σ曲线求一阶偏导数可得到-dθ/dσ-σ曲线，曲线中的最小值所对应的真应力即为临界应力，如图7所示。对比图7中各图可知，临界应力随温度的增加和应变速率的降低而降低。

由表3可知，发生动态再结晶的临界应变与峰值应变的平均比值εc/εp=0.517。应变速率对临界应变和峰值应变均产生正的影响，即随着应变速率的增加，临界应变和峰值应变都相应地提高。这是由于动态再结晶是晶核的形成、长大及大角度晶界迁移的过程。新晶核的形成机制分别为晶界弓出形核机制、亚晶合并机制及亚晶吞噬机制。形核机制均与位错的迁移、合并相关。当材料热变形时的应变速率较低时，变形晶粒内部产生的位错将有充裕的时间进行迁移、合并从而形成大角度晶界，构成再结晶的核心[19,20]。而当应变速率升高时，晶粒内部的位错将没有充足的时间完成晶界的迁移，这就需要增加变形量来增加位错密度以及延长位错迁移的时间，从而导致动态再结晶所需要的临界应变增加[21]。变形温度对临界应变和峰值应变的影响则为负，即随变形温度的增加，则临界应变和峰值应变降低。这是由于变形温度升高，提高了位错迁移的驱动力，位错更加容易迁移，从而使材料在较小的变形下就能形成新的动态再结晶晶粒。

2.5 临界应变预测模型

目前广泛采用Sellars模型[22,23]，即εc=a×Zb。其中a，b均为常数；Z为Zener-Hollomon参数，如式(2)所示。结合所求的Q，可以建立不同热变形条件下的临界应变(εc)与其相对应的Z值，绘制出lnεc与lnZ的关系曲线，如图8所示。由图8可见，lnεc与lnZ之间呈现较高的线性关系，对其进行线性拟合，可得拟合方程：lnεc=0.148lnZ-7.062，即临界应变预测模型可表示为εc=8.57×10-4Z0.148。图9为ε与lnZ的关系，在本实验条件下，SA508Gr.4N钢的临界应变与峰值应变均随Z参数的增大而增加， 且与Z参数有较好的线性关系。

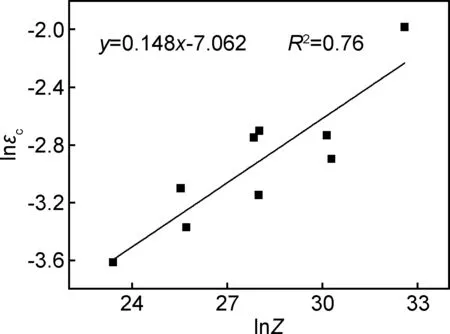
图8 lnεc与lnZ之间的关系Fig.8 Relationship between lnεc and lnZ

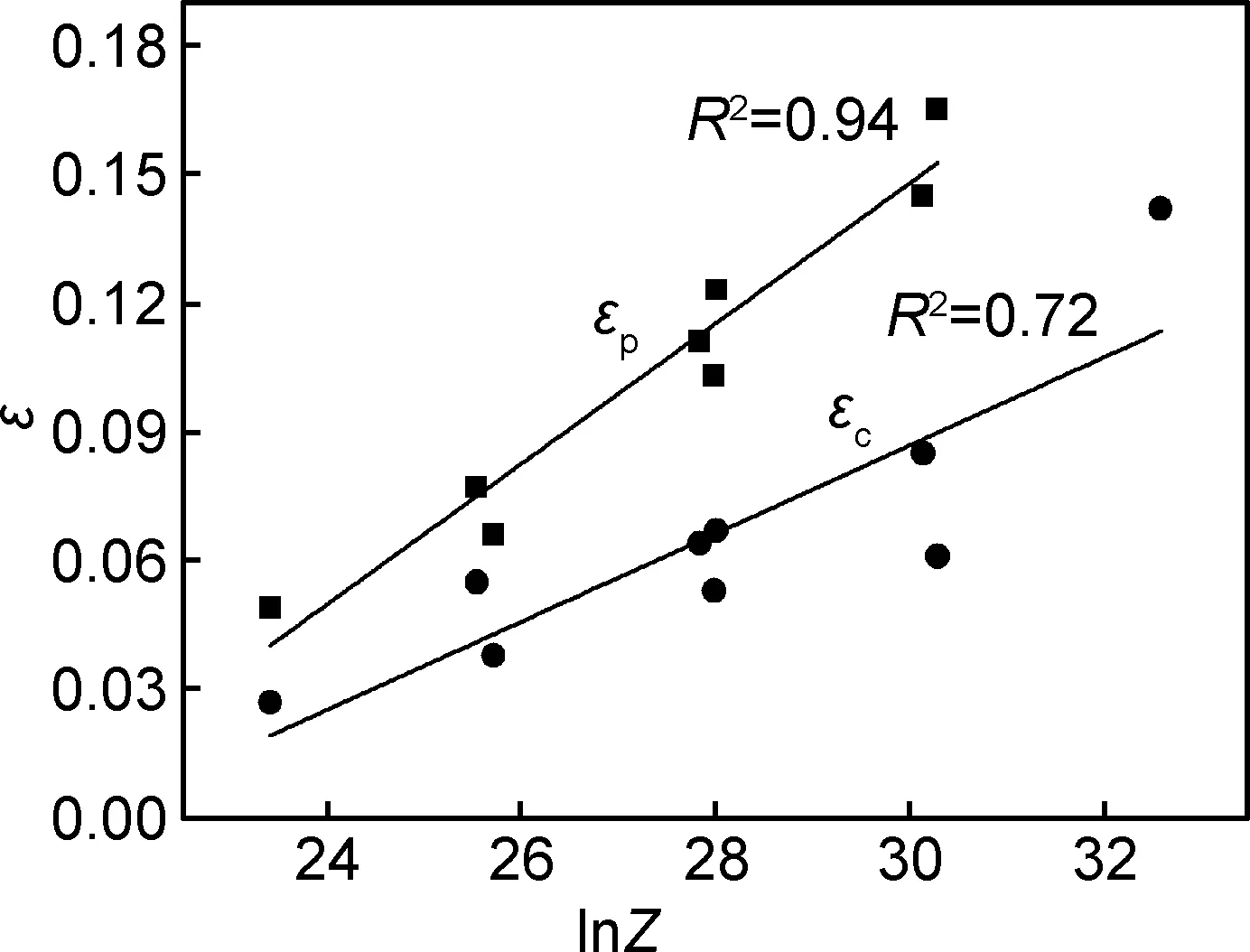
图9 lnZ与临界应变及峰值应变之间的关系Fig.9 Relationship between εc,εp and lnZ

3 结论

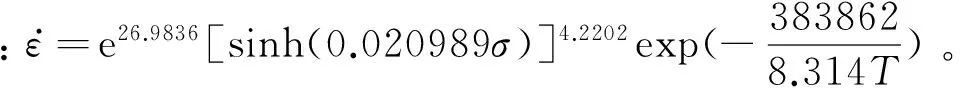
(2)SA508Gr.4N钢发生动态再结晶时，其θ-σ曲线出现拐点，并且在-dθ/dσ-σ曲线上出现极小值。利用此拐点判据，可以确定材料的动态再结晶临界条件。动态再结晶临界应变随着应变速率的增大及变形温度的降低而增加，且临界应变与峰值应变之间具有相关性，即εc/εp=0.517。

(3)在本实验条件下，引入Z参数能较好地反映临界应变与热变形条件之间的变化规律。临界应变随Z参数的增加而增大，且二者之间函数关系为：εc=8.57×10-4Z0.148。

[1] YASUHIKO T, IKUO S. Development of high purity large forgings for nuclear power plants[J]. Journal of Nuclear Materials, 2011, 417: 854-859.

[2] SUZUKI K, KURIHARA I, SASAKI T, et al. Application of high strength Mn-Mo-Ni steel to pressure vessels for nuclear power plant[J]. Nuclear Engineering and Design, 2001, 206: 261-278.

[3] 冯柳, 周邦新, 彭剑超, 等. RPV模拟钢中纳米富Cu析出相的复杂晶体结构表征[J]. 材料工程, 2015, 43(7): 80-86.

FENG L, ZHOU B X, PENG J C, et al. Characterization of a complex crystal structure within Cu-rich precipitates in RPV model steel[J]. Journal of Materials Engineering, 2015, 43(7): 80-86.

[4] 何西扣, 李昌义, 刘正东, 等. 反应堆压力容器用低合金钢平衡相热力学计算与分析[J]. 金属热处理, 2013, 38(5): 14-17.

HE X K, LI C Y, LIU Z D, et al. Thermodynamic calculation and analysis on equilibrium phase in low alloy steel for reactor pressure vessel[J]. Heat Treatment of Metals, 2013, 38(5): 14-17.

[5] JIN H H, KWON J, SHIN C S. Evolution of radiation defect and radiation hardening in heat treated SA508 Gr3 steel[J]. Nuclear Instruments and Methods in Physics Research Section B, 2014, 319: 24-28.

[6] HECTOR P R, HARRY K D H B. Continuous cooling transformations in nuclear pressure vessel steels[J]. Metallurgical and Materials Transactions A, 2014, 45(11): 4897-4906.

[7] 王小彬, 李玉光, 罗英, 等. 超临界水冷堆压力容器设计[J]. 一重技术, 2015, (3): 18-21.

WANG X B, LI Y G, LUO Y, et al. Design of supercritical water-cooled reactor pressure vessel[J]. CFHI Technology, 2015, (3): 18-21.

[8] 李昌义, 刘正东, 林肇杰, 等. 反应堆压力容器用钢的淬透性问题[J]. 材料热处理学报, 2011, 32(6): 68-72.

LI C Y, LIU Z D, LIN Z J, et al. Hardenability of nuclear reactor pressure vessel steels[J]. Transactions of Materials and Heat Treatment, 2011, 32(6): 68-72.

[9] PARK S G, LEE K H, MIN K D, et al. Characterization of phase fractions and disorientations on tempered bainitic/martensitic Ni-Cr-Mo low alloy RPV steel with various Ni content[J]. Metals and Materials International, 2013, 19(1): 49-54.

[10] PARK S G, KIM M C, LEE K H, et al. Correlation of the thermodynamic calculation and the experimental observation of Ni-Mo-Cr low alloy steel changing Ni, Mo, and Cr contents[J]. Journal of Nuclear Materials, 2010, 407: 126-135.

[11] KIM M C, PARK S G, LEE K H, et al. Comparison of fracture properties in SA508 Gr.3 and Gr.4N high strength low alloy steels for advanced pressure vessel materials[J]. International Journal of Pressure Vessels and Piping, 2015, 131: 60-66.

[12] 杨志强, 刘勇, 田保红, 等. TiC/Cu-Al2O3复合材料的强化机理及动态再结晶行为[J]. 中国有色金属学报, 2014, 24(6): 1524-1531.

YANG Z Q, LIU Y, TIAN B H, et al. Strengthening mechanism and dynamic recrystallization behavior of TiC/Cu-Al2O3composite[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1524-1531.

[13] 黄烁, 王磊, 张北江, 等. GH4706合金的热变形行为与显微组织演变[J]. 材料工程, 2015, 43(2): 41-46.

HUANG S, WANG L, ZHANG B J, et al. Hot deformation behavior and microstructure evolution of GH4706 alloy[J]. Journal of Materials Engineering, 2015, 43(2): 41-46.

[14] 陈贵清, 傅高升, 程超增, 等. 应变速率对 3003 铝合金热变形动态再结晶组织的影响[J]. 材料热处理学报, 2012, 33(10): 26-31.

CHEN G Q, FU G S, CHENG C Z, et al. Effects of strain rate on dynamic recrystallization microstructure of 3003 aluminum alloy in process of hot deformation[J]. Transactions of Materials and Heat Treatment, 2012, 33(10): 26-31.

[15] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138.

[16] 仇琍丽, 高文理, 陆政, 等. 7A85铝合金的热压缩流变行为与显微组织[J]. 材料工程, 2016, 44(1): 33-39.

QIU L L, GAO W L, LU Z, et al. Flow behavior and microstructure of 7A85 aluminum alloy during hot compression[J]. Journal of Materials Engineering, 2016, 44(1): 33-39.

[17] 袁武华, 龚雪辉, 孙永庆, 等. 0Cr16Ni5Mo低碳马氏体不锈钢的热变形行为及其热加工图[J].材料工程,2016,44(5):8-14.

YUAN W H, GONG X H, SUN Y Q, et al. Hot deformation behavior and processing map of 0Cr16Ni5Mo low carbon martensitic stainless steel[J]. Journal of Materials Engineering, 2016, 44(5): 8-14.

[18] POLIAK E I, JONAS J J. Initiation of dynamic recrystallization in constant strain rate hot deformation[J]. ISIJ International, 2003, 43(5): 684-691.

[19] 赵业青, 李岩, 鲁法云, 等. 7150铝合金热变形行为及微观组织[J]. 航空材料学报, 2015, 35(3): 18-23.

ZHAO Y Q, LI Y, LU F Y, et al. Flow stress behavior and microstructure of 7150 aluminum alloy during hot deformation [J]. Journal of Aeronautical Materials, 2015, 35(3): 18-23.

[20] 高英俊, 罗志荣, 黄礼琳, 等. 变形合金的亚晶组织演变的相场模型[J]. 金属学报, 2012, 48(10): 1215-1222.

GAO Y J, LUO Z R, HUANG L L, et al. Phase field model for microstructure evolution of subgrain in deformation alloy[J]. Acta Metallurgica Sinica, 2012, 48(10): 1215-1222.

[21] HUANG K, LOGE R E. A review of dynamic recrystallization phenomena in metallic materials[J]. Materials & Design, 2016, 111: 548-574.

[22] YANG Z Q, LIU Y, TIAN B H, et al. Model of critical strain for dynamic recrystallization in 10%TiC/Cu-Al2O3composite [J]. Journal of Central South University, 2014, 21(11): 4059-4065.

[23] FANG B, JI Z, LIU M, et al. Critical strain and models of dynamic recrystallization for FGH96 superalloy during two-pass hot deformation[J]. Materials Science and Engineering: A, 2014, 593: 8-15.

(本文责编：寇凤梅)

Hot Deformation Behavior of SA508Gr.4NSteel for Reactor Pressure Vessels

YANG Zhi-qiang1,LIU Zheng-dong1,HE Xi-kou1,LIU Ning1,2

(1 Institute for Special Steels,Central Iron and Steel Research Institute,Beijing 100081,China；2 Faculty of Material Science and Engineering,Kunming University of Science and Technology,Kunming 650093,China)

The high-temperature plastic deformation and dynamic recrystallization behavior of SA508Gr.4N steel were investigated through hot deformation tests in a Gleeble1500D thermal mechanical simulator. The compression tests were performed in the temperature range of 1050-1250℃ and the strain rate range of 0.001-0.1s-1with true strain of 0.16. The results show that from the high-temperature true stress-strain curves of the SA508Gr.4N steel, the main feature is dynamic recrystallization,and the peak stress increases with the decrease of deformation temperature or the increase of strain rate, indicating the experimental steel is temperature and strain rate sensitive material. The constitutive equation for SA508Gr.4N steel is established on the basis of the true stress-strain curves, and exhibits the characteristics of the high-temperature flow behavior quite well, while the activation energy of the steel is determined to be 383.862kJ/mol. Furthermore, an inflection point is found in theθ-σcurve, while the -dθ/dσ-σcurve shows a minimum value. The critical strain increases with increasing strain rate and decreasing deformation temperature. A linear relationship between critical strain (εc) and peak strain (εp) is found and could be expressed asεc/εp=0.517. The predicted model of critical strain could be described asεc=8.57×10-4Z0.148.

SA508Gr.4N steel;hot deformation;constitutive equation;dynamic recrystallization;critical strain

10.11868/j.issn.1001-4381.2016.000887

TG142

A

1001-4381(2017)08-0088-08

国家能源应用技术研究及工程示范项目(NY201501)；新一代核能用材发展战略研究项目(2016-ZD-06)

2016-07-21;

2017-01-12

刘正东(1966-)，男，博士，教授，研究方向为火电站、核电站和核动力用钢，联系地址：北京市海淀区学院南路76号钢铁研究总院特殊钢研究所(100081)，E-mail:liu_zhengdong@263.net