2A12铝合金的多轴加载疲劳行为

陈亚军，王先超，王付胜，刘 波

(中国民航大学 中欧航空工程师学院，天津 300300)

2A12铝合金的多轴加载疲劳行为

陈亚军，王先超，王付胜，刘 波

(中国民航大学 中欧航空工程师学院，天津 300300)

采用SDN100/1000电液伺服拉扭复合疲劳试验机对2A12铝合金进行多关键参数的多轴疲劳性能研究，通过对断口的微观分析探究疲劳失效机理。结果表明:等效应力加载条件下，随拉扭相位差的增加疲劳寿命降低，0°相位差下断面裂纹源区能观察到轮胎状、鱼骨状以及钟乳石状的特殊形貌，裂纹扩展区存在二次裂纹和模糊的疲劳条带；分别改变拉、扭平均应力，多轴疲劳寿命均降低，裂纹源区能看到白色絮状的氧化物，瞬断区存在二次裂纹和剪切型韧窝；不同加载波形条件下，正弦波对应最长的多轴疲劳寿命，三角波次之，方波时最短且体现出最大的结构耗能。低-高两级加载条件下，材料产生“锻炼效应”。

2A12铝合金；多轴疲劳；失效机理；两级加载；锻炼效应

2A12铝合金具有较高的比强度、比刚度、断裂韧度以及良好的耐腐蚀稳定性，是制造飞机结构及零部件的理想材料,其在飞机机身以及机翼的蒙皮结构、翼梁、翼肋、隔框等主要受力构件和一些非主要受力构件中均有大量应用[1，2]。多轴疲劳是指损伤发生在多轴加载条件下，加载过程中至少存在两个独立的应力(应变)分量，它们之间可能发生同相位按比例的变化，也有可能发生非同相位非比例的变化[3]。相对于单轴疲劳而言,多轴疲劳更加接近工程实际,飞机在起降过程中，其构件往往受到多轴载荷的作用，因此，这方面的研究对飞行安全评估具有非常重要的价值[4-7]。目前国外对多轴疲劳的研究多集中于疲劳寿命预测模型及疲劳破坏准则的分析上：Susmel等[8]提出了一种新的基于临界面法的多轴疲劳寿命预测方法；Han等[9]对多轴常幅下常用的疲劳破坏准则在多轴变幅加载下的疲劳预测能力进行了研究；Ahmadi等[10]认为微裂纹扩展分为微观短裂纹阶段和物理短裂纹阶段，并提出了用连续损伤力学理论对裂纹扩展进行表述。国内研究方面，尚德广等[11]结合多轴疲劳损伤的特点，对Chaboche连续损伤力学累积模型进行修改，建立了多轴非线性疲劳损伤累积模型；何国求等[12]利用316L不锈钢对多轴非比例加载下低周疲劳寿命估算方法进行了讨论。目前相关研究多集中在薄壁管件[13-16]和民用钢铁实心构件[17，18]的多轴疲劳失效理论及寿命预测方面，而模拟飞机航空材料实心构件多轴疲劳的相关实验研究较少。本工作考虑某型单旋翼直升机的尾旋翼实心变距拉杆的实际尺寸和多轴受力情况，采用2A12航空铝合金实心试样进行实验研究。分别研究了不同相位差、不同平均应力、不同加载波形以及两级载荷加载条件下的多轴疲劳寿命，并对试样断口微观形貌进行扫描电镜分析，研究了多轴疲劳裂纹萌生及扩展机理。

1 实验材料与方法

实验材料为2A12铝合金,化学成分为：Cu 3.8%～4.9%(质量分数，下同), Mg 1.2%～1.8%, Mn 0.3%～0.9%,其余为Al和其他一些杂质。其室温基本拉伸性能为:σs=373.7MPa,σb=526.8MPa,E=78.5GPa。试样采用实心圆柱形，具体尺寸如图1所示。

多轴疲劳实验在SDN100/1000电液伺服拉扭复合试验机上进行，采用拉压和扭转双通道控制方法，加载频率f=5Hz,实验环境为室温大气,疲劳破坏定义为试件的完全断裂。实验采用正弦波加载，具体表达式如下：

σ=σasin(ωt)

(1)

τ=τasin(ωt-φ)

(2)

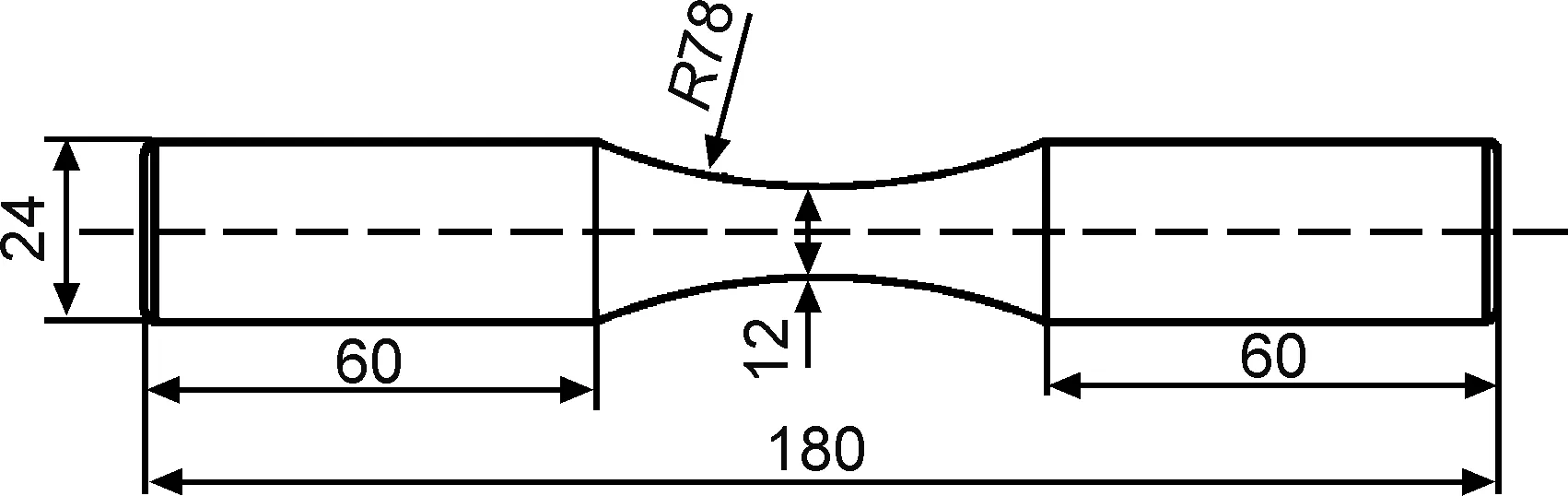
图1 疲劳试件尺寸示意图Fig.1 Schematic illustration of the fatigue specimen

式中：σa，τa为正应力和切应力的幅值；ω为实验角频率；t为实验加载时间；φ为轴向正应力与法向切应力之间的瞬时相位差。加载时取等效应力为Von Mises应力，应力幅比γ定义为拉压应力幅与扭转应力幅之比，即：

σeq=(σ2+3τ2)1/2

(3)

γ=σa/τa

(4)

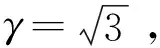
使用Hitachi S-3400N扫描电子显微镜对疲劳断口进行观察和分析，以探究多轴疲劳断裂的微观机制。

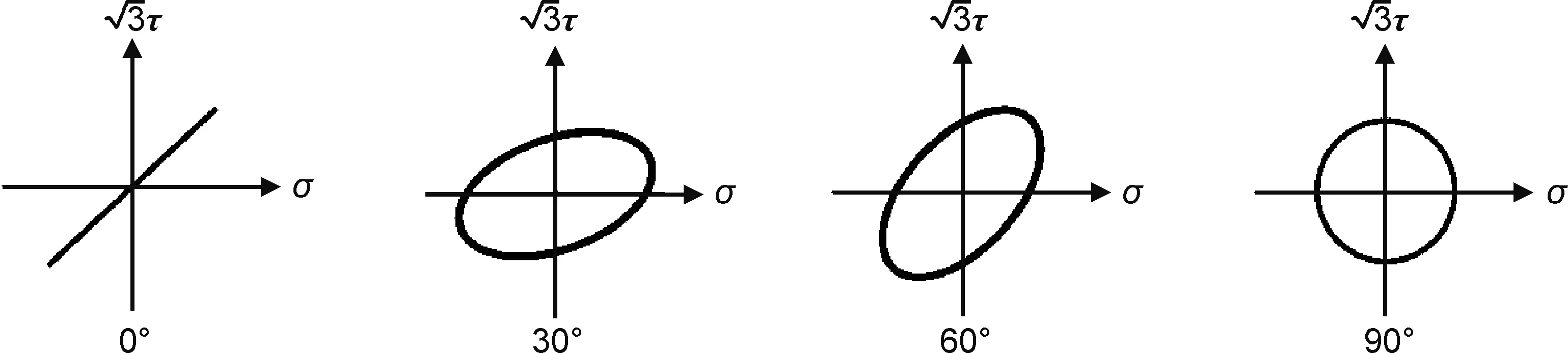
图2 相位差0°，30°，60°，90°时载荷的加载路径Fig.2 Loading paths for the different phase angles of 0°,30°,60°,90°

2 结果与分析

2.1 相位差变量实验

2.1.1 实验结果

等效应力加载条件下，0°相位差时平均疲劳寿命最高，为20946周，90°相位差时平均疲劳寿命最短，为13910周，不同相位差下的疲劳寿命相差达数千周次。图3为2A12铝合金在不同相位差下的疲劳寿命分布，由图3可知随相位差的增加，2A12铝合金的多轴疲劳寿命逐渐降低。这是由于随相位差的增加，正应力和切应力达到最大值的时间差增大，正应力和切应力分别作用的效果更加明显，使得2A12铝合金的多轴疲劳寿命随相位差的增加而降低。

2.1.2 多轴加载损伤特征

在上述多轴疲劳实验中,由于正应力和切应力之间相位差的不同,断口外部形貌也存在一定的差异。图4为不同加载相位差下试样的断裂形貌，可以观察到，疲劳断面与试样主轴之间的夹角随相位差的增加逐渐变大，90°相位差时断口几乎与主轴垂直，呈现出类似于纯扭转加载时的断口外观形貌。可见，随着相位差的增加，切应力对疲劳寿命的影响逐渐变大，切应力单独作用能力的增强造成疲劳寿命的降低。

图3 多轴疲劳寿命与相位差的关系曲线Fig.3 Relation curve of multiaxial fatigue life and phase angle

图4 不同相位差下试样的断裂形貌(a)0°；(b)30°；(c)60°；(d)90°Fig.4 Morphologies of fatigue fracture under different phase angles(a)0°；(b)30°；(c)60°；(d)90°

不同相位差下的疲劳断口明显分为裂纹源区、裂纹扩展区和瞬断区3个区域，不同相位差下疲劳断口的微观形貌相差较大。图5为试样疲劳断口裂纹扩展区的微观形貌，从图5(a)中可以看出相位差为0°的比例加载下，主裂纹左侧存在模糊的疲劳条带，条带的扩展方向与主裂纹垂直。在多轴加载条件下，由于切应力所产生的摩擦作用，疲劳条带变得不再明显。另外，在图5(a)中还可以观察到与主裂纹近似垂直的二次裂纹，产生的原因在于主裂纹扩展的同时伴随着一些微裂纹的萌生，当断裂面主裂纹经过新萌生的微裂纹后，这些新萌生的细小裂纹就会停止扩展留存下来。从图5(a)到图5(d)，随着相位差的增加，擦伤痕迹开始增多，非比例加载下的疲劳断口扩展区已经很难观察到疲劳条带。这是由于非比例加载条件下切应力的破坏作用越来越明显，切应力绕主轴的往复旋转磨去了正应力作用下产生的疲劳条带，在断口表面形成了更多的划痕。

图6为0°比例加载条件下疲劳试样断口在扫描电镜下观察到的特殊形貌。从图6(a)裂纹源区中可以观察到轮胎状和鱼骨状形貌，这是多轴比例加载条件下高周疲劳断口的局部特殊形貌。疲劳裂纹形成后，在正应力的反复作用下，裂纹面两侧做有规律的张合运动，由于面上的脊棱或夹杂物的摩擦作用，造成了断面上出现轮胎状花样的擦痕。图6(b)中左侧呈现串状凸起形貌，右侧有类似于钟乳石状的形貌，中间小平台由于切应力的作用产生两道裂纹，被分成3段。图6(b)中的特殊形貌可能是在扭转应力作用下发生切向破坏造成的结果。

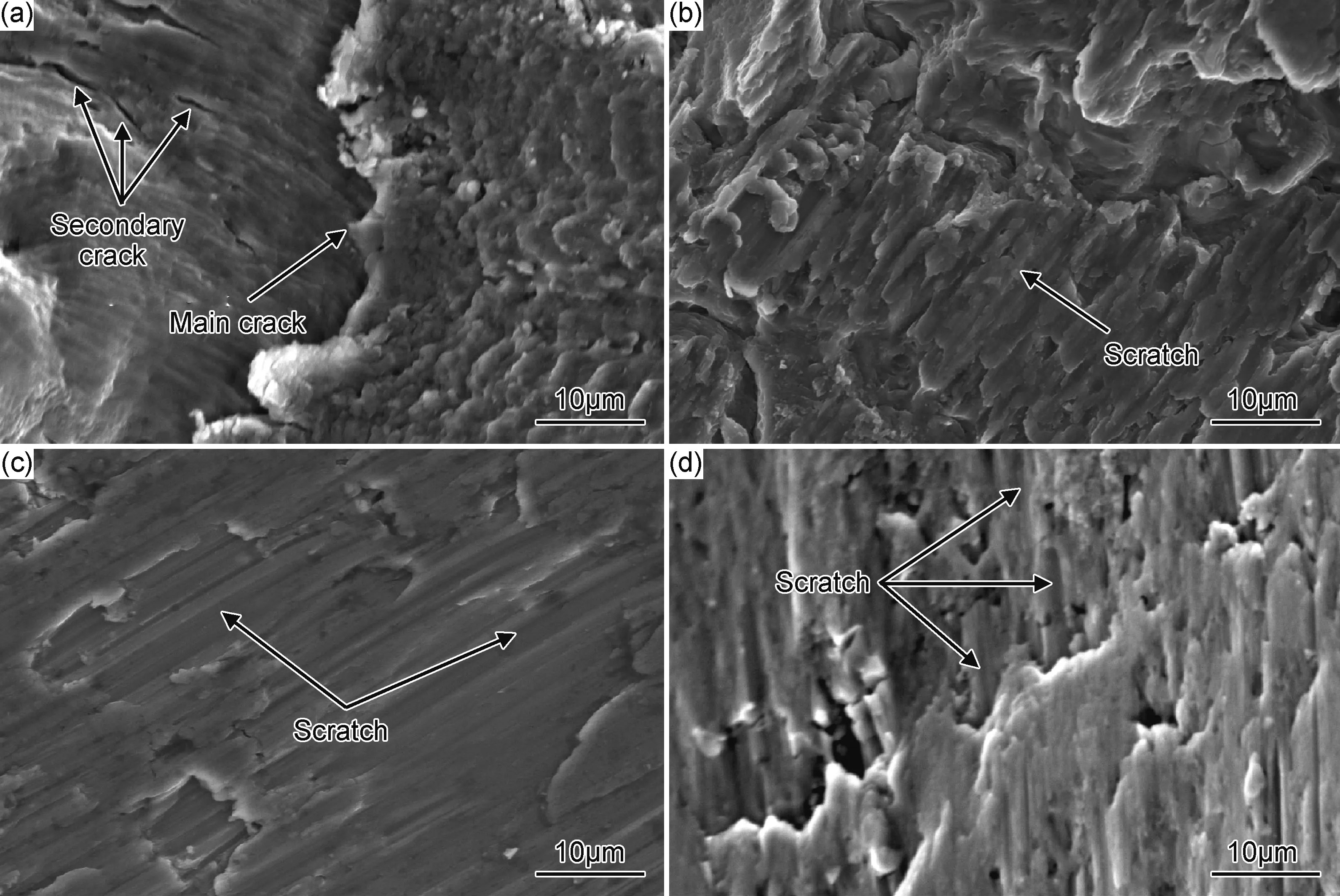
图5 不同相位差下裂纹扩展区SEM形貌图 (a)0°；(b)30°；(c)60°；(d)90°Fig.5 SEM morphologies of crack propagation zone under different phase angles(a)0°；(b)30°；(c)60°；(d)90°

图6 0°比例加载条件下特殊断口SEM形貌图 (a)裂纹源区；(b)裂纹扩展区Fig.6 Special fracture features under the phase angle of 0° (a)crack initiation zone;(b)crack propagation zone

2.2 平均应力变量实验

2.2.1 实验结果

图7为不同拉、扭平均应力值与多轴疲劳寿命间的关系曲线，从图7可知当拉、扭平均应力为0MPa时，试样的疲劳寿命最长，为20946周。在等效应力幅值不变的条件下，随拉、扭平均应力值的增大或减小，试样的疲劳寿命都会缩短，其中拉压应力幅为35.4MPa和-35.4MPa时，材料的平均疲劳寿命分别为11164周和9936周；扭转应力幅为20.6MPa和-20.6MPa时，材料的平均疲劳寿命分别为14798周和12249周。由正应力产生的轴向拉压对疲劳裂纹的扩展起着主导作用,而切应力绕轴的扭转对于裂纹的萌生贡献最大。切向应力平均值保持不变，当轴向应力平均值变大(变小)时，拉向(压向)应力幅值增大，裂纹扩展速率的加快降低了试样的疲劳寿命；轴向应力平均值保持不变，当切向应力平均值变大(变小)时，切向应力幅增大，裂纹萌生的速率加快导致疲劳寿命缩短。

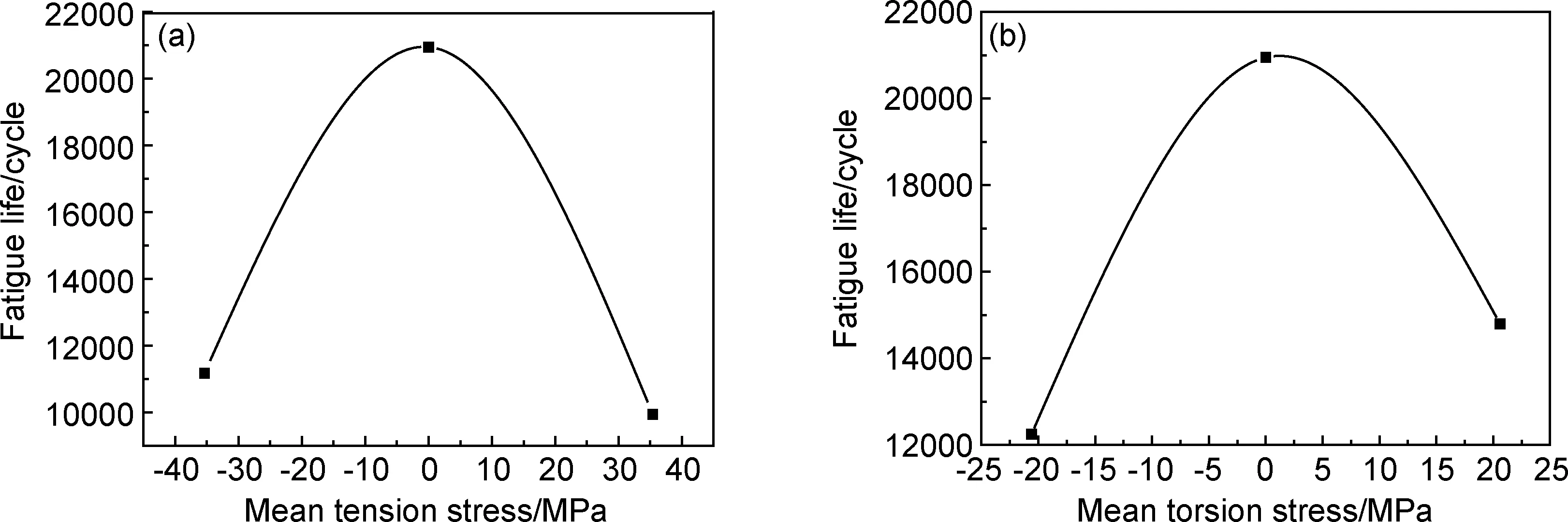
图7 拉(a)、扭(b)平均应力与疲劳寿命关系曲线Fig.7 Relation curves of fatigue life and mean stress of tension(a) and torsion(b)

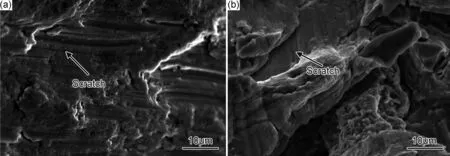
图8 拉压平均应力为-35.4MPa的断口SEM图像 (a)裂纹源区；(b)裂纹扩展区Fig.8 Fracture SEM morphologies under the mean tension stress of -35.4MPa(a)crack initiation zone；(b)crack propagation zone

图9 扭转平均应力为20.6MPa的断口SEM图像 (a)裂纹扩展区；(b)瞬断区Fig.9 Fracture SEM morphologies under the mean torsion stress of 20.6MPa (a)crack propagation zone；(b)instantaneous fracture zone

2.2.2 多轴加载损伤特征

对不同拉、扭平均应力下的疲劳断口进行扫描电镜观察，图8和图9分别为-35.4MPa和20.4MPa拉、扭应力平均值下裂纹不同扩展时期的微观形貌。从图8可以观察到，在拉压平均应力为-35.4MPa时，疲劳断口的裂纹源区(图8(a))以及裂纹扩展区(图8(b))中都存在明显的划痕，这主要是在切应力绕轴旋转作用下所产生的。拉压应力平均值的减小使得压向应力幅值变大，裂纹面两侧的受压程度增加，垂直于轴向的旋转作用对裂纹面两侧的碾磨作用变得更强，所产生的破坏影响也更为显著，因此会在断口观察到大量较为明显的划痕。如图9所示，在扭转应力为20.6MPa时，疲劳断口扩展区(图9(a))形貌凹凸不平，没有观察到疲劳条带、二次裂纹等特征形貌。切应力的不对称加载使得断面受力情况变得复杂，加载产生的疲劳条带以及二次裂纹等形貌可能在不对称扭转作用下遭到了破坏。瞬断区(图9(b))中可以观察到二次裂纹和韧窝的存在。图9(b)中的韧窝呈现剪切拉长形貌，这是扭转疲劳断口的典型特点，与扩展区相比，由于瞬断区持续的时间较短，使得这些特征形貌得以保存下来。同时，在疲劳断口裂纹源附近发现了大量的白色絮状物质，如图10所示。对图10中白色絮状物质进行能谱分析，得到图11所示的絮状物能谱分析图。分析结果表明，白色絮状物质中主要含有氧、铝、铜3种元素，其质量分数分别为47.2%，51.2%和1.5%，可以推断此处在裂纹初始形成时生成了铝的氧化物。

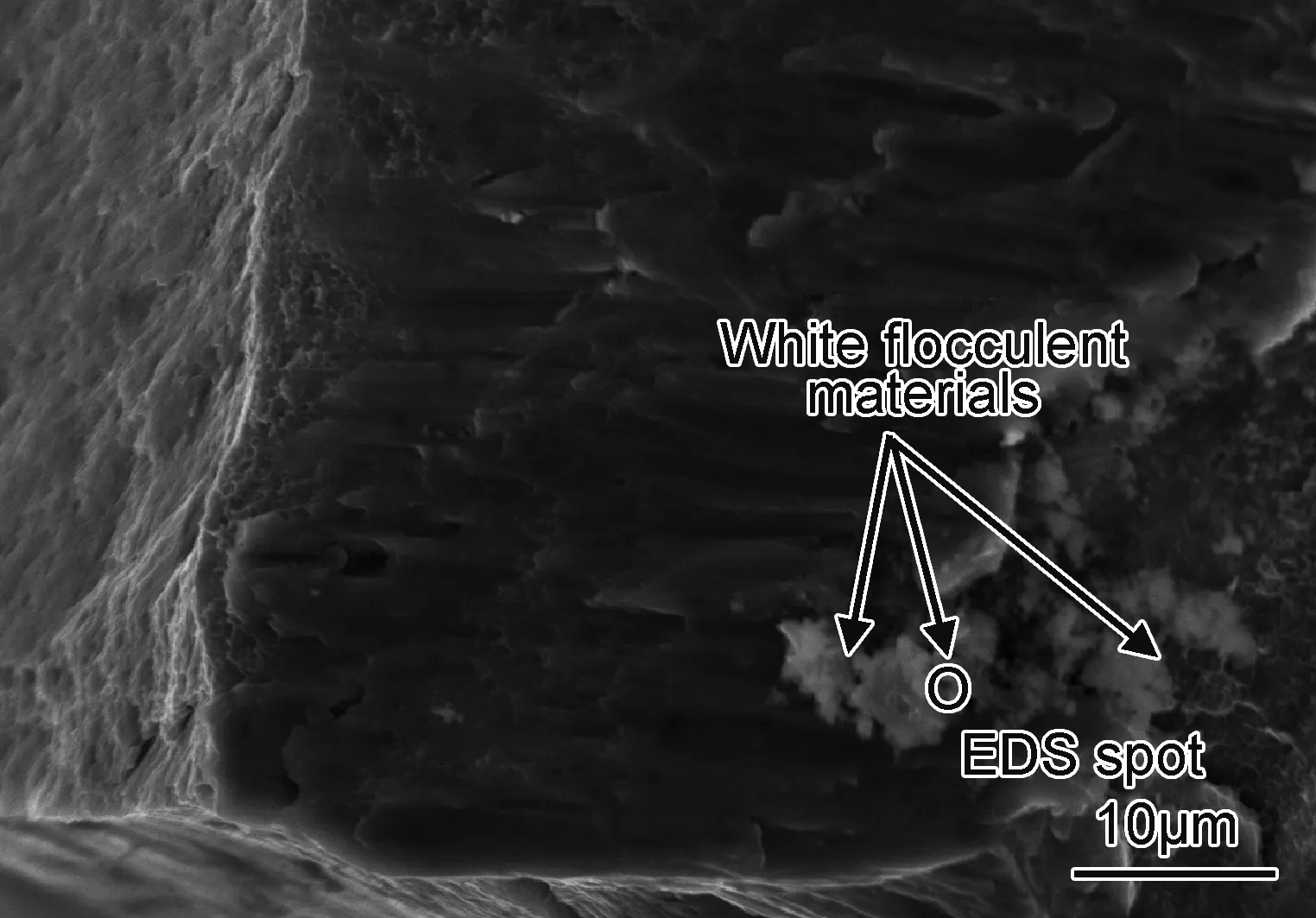
图10 裂纹源区的白色絮状物质Fig.10 White flocculent materials in the crack initiation zone

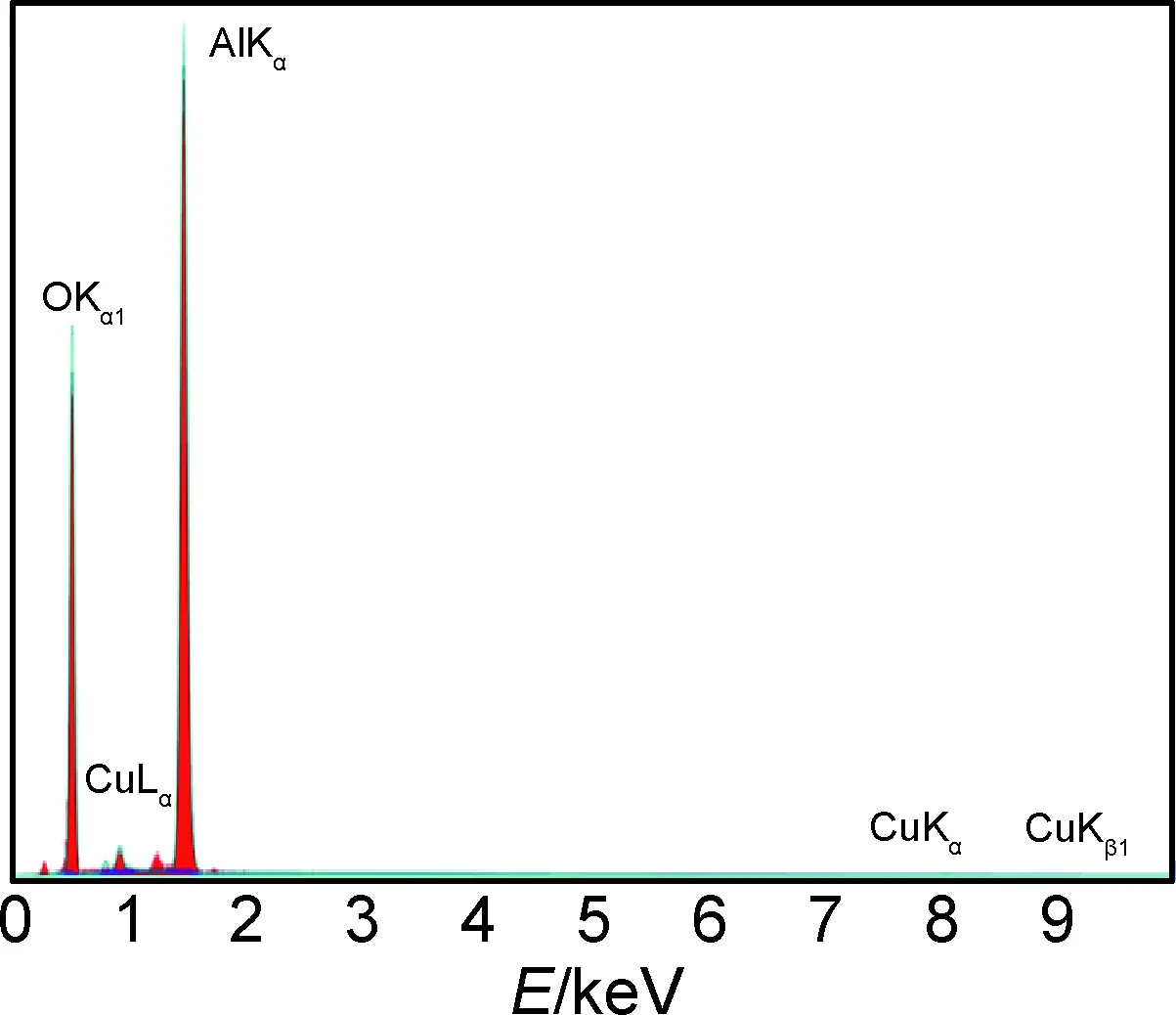
图11 裂纹源区白色絮状物质能谱图Fig.11 EDS analysis of white flocculent materials in the crack initiation zone

2.3 加载波形变量实验

2.3.1 实验结果

分别使用正弦波、三角波、方波及3种波形的组合进行实验，得到5种不同加载情况下试样的多轴疲劳寿命。其中，三角波加载条件下试样平均疲劳寿命为16502周，方波时为12387周，两种组合波形下疲劳寿命相差不大，分别为18607周和18957周。图12为加载波形与相应疲劳寿命之间的关系，从图12可知，在等效应力保持不变的情况下，加载波形的选择对试样多轴疲劳寿命产生较大的影响。采用方波加载时疲劳寿命最短，正弦波加载疲劳寿命最长，三角波加载疲劳寿命介于两者之间。三角波加载方式使拉、扭应力在幅值处瞬间发生变化，对试样组织结构的破坏程度大于正弦波加载。方波加载方式在拉、扭载荷达到幅值时都会有一段时间的应力保持，这种持续高应力的作用以及应力方向的瞬间改变形式造成了试样多轴疲劳寿命的大幅度缩短。组合波形加载模式下，疲劳寿命介于正弦波和三角波加载寿命之间，且不同的加载顺序对多轴疲劳寿命影响不大。

图12 波形-多轴疲劳寿命关系Fig.12 Relations of waveform and multiaxial fatigue life

2.3.2 不同波形加载下循环曲线分析

通过采集多轴疲劳实验循环过程中的相关数据，分析不同波形加载条件下的循环特征。图13为3种波形加载下轴向负荷与位移以及扭矩与扭角之间的循环关系曲线。3种波形在轴向负荷与位移以及切向扭矩与扭角之间都出现不同程度的迟滞现象，方波作用下迟滞现象最为明显，三角波次之，正弦波加载迟滞现象最小。滞回曲线所包围的面积能反映结构耗散能量的大小，这些能量通过材料变形的内摩擦阻力或者是产生裂纹等局部损伤最终转化为热能耗散到大气中。相同等效应力条件下，2A12铝合金材料在不同波形加载模式下有着不同的结构耗能能力，方波加载模式下体现出了更大的结构耗能。

2.4 两级加载实验

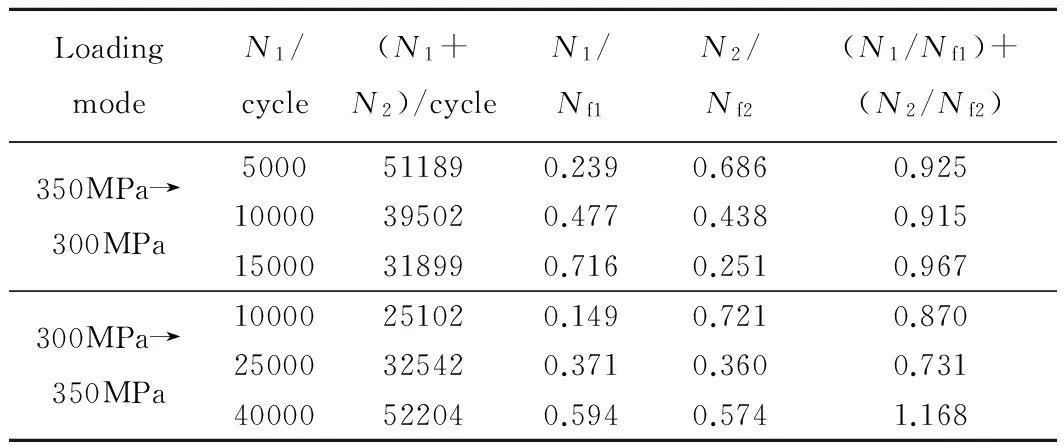
首先，通过疲劳实验测得等效载荷为350MPa和300MPa时平均疲劳寿命分别为20946周和67338周。然后进行两组两级变幅多轴疲劳实验，分别改变一级载荷作用下的循环周次，得到不同加载条件下平均疲劳寿命如表1所示。其中N1，N2分别为一级、二级载荷的循环周次，Nf1，Nf2分别为仅在第一、二级载荷作用下试样的疲劳寿命。

图14为一级循环周次与整体疲劳寿命的关系曲线，从图中可以看出随一级载荷循环周次的增加，高-低加载模式下试样的多轴疲劳寿命降低，低-高加载模式下，疲劳寿命呈上升趋势。等效应力加载条件下，较高的应力幅值有助于疲劳裂纹的萌生和扩展，对试样产生的破坏作用较强，进而加速了疲劳断裂。图15所示为一级损伤比N1/Nf1与二级损伤比N2/Nf2之间的关系曲线。高-低加载模式下，随一级损伤比的增加，二级损伤比线性降低，从表1中可以看出两级损伤比之和相差不大。低-高加载模式下，一级损伤比从0.149增加到0.371时，二级损伤比从0.721降低到0.360，继续增加一级损伤比到0.594，二级损伤比不降反升，表现为增加低应力载荷的循环周次，试样断裂前高应力载荷的循环周次也出现增加，表现出“锻炼效应”的特征。

图13 不同波形加载方式轴向、扭向循环滞回线(a)正弦波；(b)三角波；(c)方波；(1)轴向载荷与位移；(2)扭矩与扭角Fig.13 Hysteresis loops of tension-torsion under different waveforms(a)sine wave;(b)triangle wave;(c)square wave;(1)axial loading and displacement;(2)moment of torsion and torsion angle

LoadingmodeN1/cycle(N1+N2)/cycleN1/Nf1N2/Nf2(N1/Nf1)+(N2/Nf2)350MPa→300MPa300MPa→350MPa5000511890.2390.6860.92510000395020.4770.4380.91515000318990.7160.2510.96710000251020.1490.7210.87025000325420.3710.3600.73140000522040.5940.5741.168

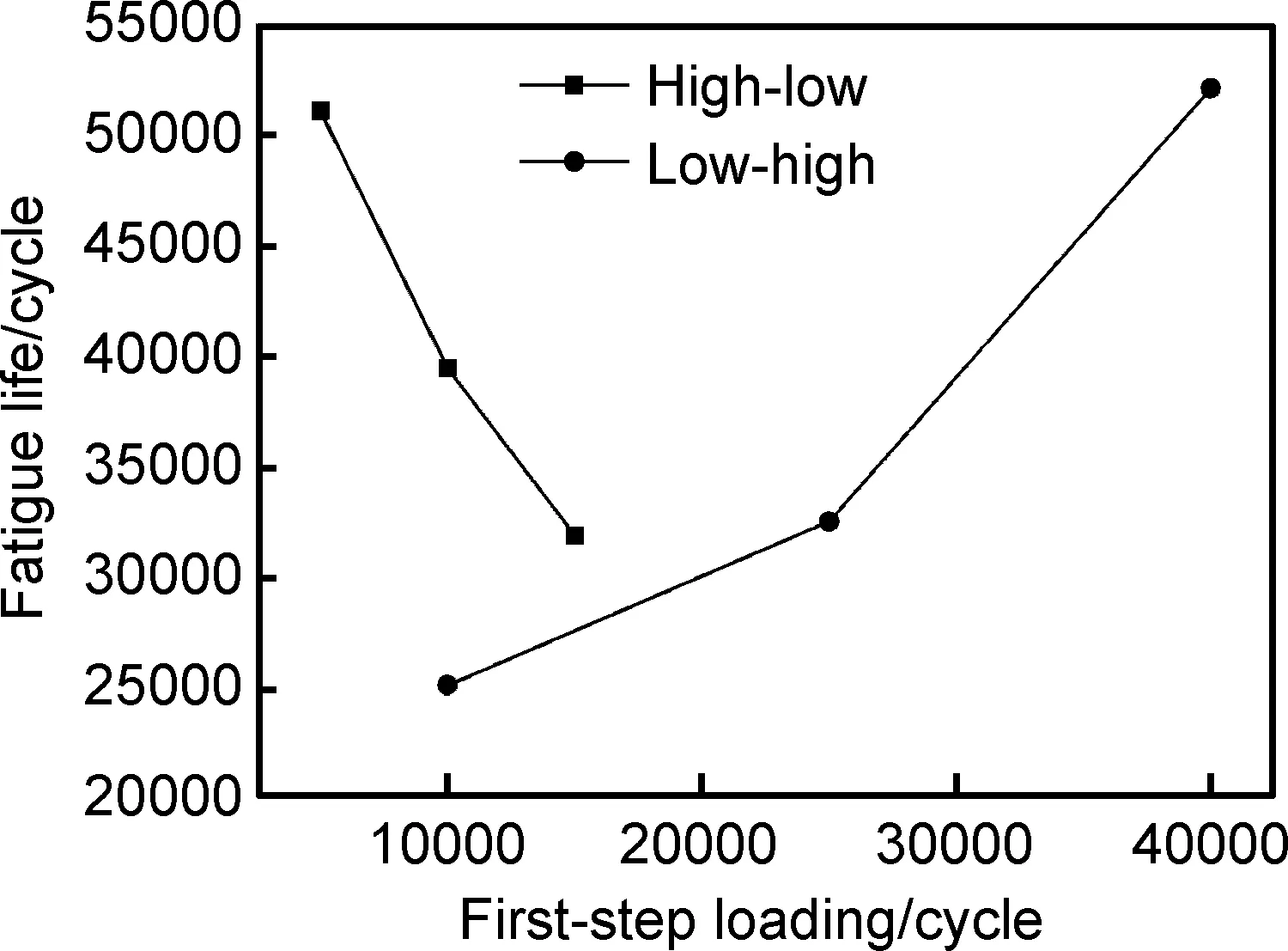
图14 一级载荷循环周次-整体疲劳寿命关系曲线Fig.14 Relation curves of the cycle numbers of first step loading and the total fatigue life

图15 一级损伤比与二级损伤比关系曲线Fig.15 Relation curves of the first and the second step damage ratios

3 结论

(1)相位差从0°增大到90°，疲劳寿命从20946周逐渐递减到13910周。试样断面与主轴的夹角随相位差的增加逐渐变大，90°时呈现出类似于纯扭转加载时的外观断口形貌。0°比例加载下能观察到疲劳条带和二次裂纹，以及类似于鱼鳞、鱼骨、钟乳石等的特殊微观形貌。

(2)随拉、扭平均应力值的增大或减小，试样的疲劳寿命缩短。拉压应力平均值为-35.4MPa时，在断面的裂纹源区以及裂纹扩展区都能观察到大量明显的划痕。扭转应力为20.6MPa时，断口扩展区疲劳条带等特征形貌不明显，在瞬断区可以观察到二次裂纹和韧窝的存在。疲劳源区白色絮状物经能谱分析为裂纹萌生阶段形成的铝的氧化物。

(3)方波加载时多轴疲劳寿命最短，三角波加载方式对试样组织结构的破坏程度大于正弦波加载，但疲劳寿命大于方波加载方式。3种波形加载方式下都出现不同程度的迟滞现象，方波加载体现出更大的结构耗能。高-低两级加载模式下，随一级循环周次的增加，整体疲劳寿命逐渐降低；低-高加载模式下，随一级循环周次的增加，出现“锻炼效应”的特征。

[1] 中国航空材料手册编委会.中国航空材料手册：第3卷 铝合金 镁合金 钛合金[M].北京：中国标准出版社，1989.

[2] STALEY J T, LIU J, HUNT W H Jr. Aluminum alloys for aerostructures[J]. Adv Mater Proc,1997,152(4):17-20.

[3] 尚德广，王德俊.多轴疲劳强度[M].北京:科学出版社，2007.

SHANG D G, WANG D J. Multiaxial Fatigue Strength[M]. Beijing: Science Press, 2007.

[4] 张成成.复杂应力场下结构高周疲劳寿命分析[D].南京：南京航空航天大学，2010.

ZHANG C C. Analysis of high cycle fatigue life of structures under complex stress field[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.

[5] XU X L, YU Z W. An investigation on the failed blades in a locomotive turbine[J]. Engineering Failure Analysis, 2007,14(7):1322-1328.

[6] 王明春，宋恩鹏，赵清华.基于应力场强方法的多轴疲劳寿命分析及应用[J].飞机设计，2015，35(4)：10-13.

WANG M C, SONG E P, ZHAO Q H. The prediction of multiaxial high cycle fatigue based on stress field intensity[J]. Aircraft Design, 2015,35(4):10-13.

[7] 童第华，吴学仁，刘建中，等.基于小裂纹理论的铸造钛合金ZTC4疲劳寿命预测[J].材料工程，2015，43(6)：60-65.

TONG D H, WU X R, LIU J Z, et al. Fatigue life prediction of cast titanium alloy ZTC4 based on the small crack theory[J]. Journal of Materials Engineering, 2015,43(6):60-65.

[8] SUSMEL L，LAZZARIN P. A bi-parametric Wöhler curve for high cycle multiaxial fatigue assessment[J]. Fatigue Fract Eng Mater Struct, 2002,25(1):63-78.

[9] HAN C, CHEN X, KIM K S. Evaluation of multiaxial fatigue criteria under irregular loading[J]. International Journal of Fatigue,2002,24(9):913-922.

[10] AHMADI A, ZENNER H. Lifetime calculation under multiaxial random loading with regard to the microcrack growth[C]//7th International Conference on Biaxial/Multiaxial Fatigue and Fracture.Berlin:European Structural Integrity Society,2004:415-420.

[11] 尚德广,王德俊,姚卫星.多轴非线性连续疲劳损伤累积模型的研究[J].固体力学学报，1999，20(4)：325-330.

SHANG D G, WANG D J, YAO W X. Study on nonlinear continuum multiaxial fatigue cumulative damage model[J]. Acta Mechanica Solida Sinica,1999,20(4):325-330.

[12] 何国求，丁向群，朱正宇，等.新的多轴非比例加载低周疲劳寿命估算公式[J].机械强度，2004，26(增刊1)：258-262.

HE G Q, DING X Q, ZHU Z Y, et al. New low cycle fatigue life criterion under nonproportional loading[J].Journal of Mechanical Strength,2004,26(Suppl 1):258-262.

[13] McDIAMID D L. A general criterion for high cycle multiaxial fatigue failure[J]. Fatigue Fract Eng Mater Struct,1991,14(4):429-453.

[14] WANG C H, BROWN M W. A path-independent parameter for fatigue under proportional and non-proportional loading[J]. Fatigue Fract Eng Mater Struc,1993,16(12):1285-1297.

[15] KIM K S,PARK J C. Shear strain based multiaxial fatigue parameters applied to variable amplitude loading[J]. International Journal of Fatigue,1999,21(5):475-483.

[16] 夏天翔，姚卫星，许利蒲. LY12CZ铝合金在多轴两级阶梯谱下疲劳累积损伤理论的对比研究[J]. 航空材料学报，2014，34(3)：86-92.

XIA T X, YAO W X, XU L P. Comparative research on accumulative damage models under multiaxial 2-stage step loading spectra for LY12CZ aluminium alloy[J]. Journal of Aeronautical Materials,2014,34(3):86-92.

[17] REIS L, LI B, DE F M. Analytical and experimental studies on fatigue crack path under complex multi-axial loading[J]. Fatigue Fract Eng Mater Struct, 2006, 29(4):281-289.

[18] 刘古峰.钻杆用钢复合加载疲劳断裂及规律性研究[D].西安：西安石油大学, 2011.

LIU G F. Drill pipe steel under combined loads fatigue fracture and regularity research[D].Xi’an:Xi’an Shiyou University,2011.

(本文责编：齐书涵)

Fatigue Behavior of 2A12 Aluminum Alloy Under Multiaxial Loading

CHEN Ya-jun,WANG Xian-chao,WANG Fu-sheng,LIU Bo

(Sino-European Institute of Aviation Engineering,Civil Aviation University of China,Tianjin 300300,China)

The multiaxial fatigue behavior of 2A12 aluminum alloy was studied with SDN100/1000 electro-hydraulic servo tension-torsion fatigue tester under multiple variables, and the failure mechanism was investigated by scanning electron microscopy (SEM). The results show that under the loading condition of equivalent stress, the fatigue life decreases with the increase of phase angle. For the phase angle 0°, some special features can be observed in the crack initial zone, such as the tire pattern,fishbone pattern and stalactite pattern. There are secondary cracks and vague fatigue striations in the crack propagation zone; the multiaxial fatigue life decreases with the change of mean stress for tension or torsion. Some white flocculent oxides can be found in the crack initiation zone, and secondary crack as well as shear-type elongated dimples in the instantaneous fracture zone; facing different loading waveforms, the multiaxial life of sine wave is the longest, triangle wave in the second place, and the square wave is the shortest, under the loading condition of equivalent stress, square wave leads to the maximum structural energy dissipation. Under the low and high two step loading, 2A12 shows training effect.

2A12 aluminum alloy;multiaxial fatigue;failure mechanism;two-step loading;training effect

10.11868/j.issn.1001-4381.2015.001451

O346.2

A

1001-4381(2017)08-0068-08

国家自然科学基金项目(11502285); 中央高校基本科研业务费项目中国民航大学专项(3122017112)

2015-11-26;

2017-05-09

陈亚军(1976-)，男，副教授，博士，研究方向为飞机结构材料失效分析，联系地址：天津市中国民航大学(北院)中欧航空工程师学院(300300)，E-mail:2292598008@qq.com