基于模糊熵评价和最优搜索的自动对焦算法

刘书炘，刘满华

(1.闽南师范大学 教育科学学院，漳州 福建 363000；2.上海交通大学 电子信息与电气工程学院，上海 200240)

基于模糊熵评价和最优搜索的自动对焦算法

刘书炘1，刘满华2

(1.闽南师范大学 教育科学学院，漳州 福建 363000；2.上海交通大学 电子信息与电气工程学院，上海 200240)

针对传统自动对焦算法不能实现最优对焦，以及易受清晰度评价函数局部峰值影响，从而导致重复性和稳定较差的问题，提出一种基于模糊熵的清晰度评价算法和全局最优拟合算法，应用于工业影像测量的自动对焦。该算法用模糊熵对图像清晰度进行评价，可降低噪声以及放大倍率和光照强度变化对自动对焦性能的影响，结合多尺度全局搜索和微尺寸曲线拟合搜索算法，避免局部峰值的干扰以实现最优对焦。该算法在环境变化的条件下，尤其是针对光照不稳定和变倍精度不够高的环境下，具有很高的聚焦精度，重复性和稳定性有显著提升，能够满足工业影像测量对自动对焦的要求。通过实际工业影像测量系统中的应用对比试验，该算法的有效性和优越性得到了验证。

自动对焦；模糊熵；清晰度评价；全局搜索；曲线拟合；最优对焦

0 引 言

基于图像技术的非接触式测量因其快捷、方便、智能等特点而被广泛应用到工业测量，机器人，医学生物等多个领域。工业影像测量的任务是基于所获取的图像对工件的尺寸进行计算，因此，获取高清晰的图像就成为工业影像测量的首要任务。自动对焦是影像测量系统中获取清晰图像的重要过程，成为影像测量的关键技术[1]，它通过选择适当的清晰度评价函数对采集的图像进行评价，根据评价结果，应用搜索算法搜寻图像的对焦位置，然后驱动调焦机构使电荷耦合元件(charge-coupled device，CCD)快速准确到达焦点位置。

R. Redondo等[2]针对细胞组织图像，分析了16种不同清晰度评价函数的运算量、精度、噪声和照明条件等的影响。A. Akiyama等[3]提出一种基于Daubechies小波变换的清晰度评价函数，并应用于非制冷红外相机上，但是对环境环境参数很敏感，难以用于工业测量。针对低光照条件下清晰度评价函数曲线平坦的问题，M. Gamadia等[4]提出通过图像增强增加图像对比度，再设计合适的清晰度评价函数测量图像对比度。Liu等[5]针对爬坡算法容易陷入局部极值的缺陷，采用调制传递函数(modulation transfer function，MTF)对爬坡算法进行改进，经纬仪试验结果表明，该算法能实现精确有效的对焦，有效解决了局部峰值对搜索的影响，但是对焦时间长、实时性差。Lu等[6]提取边缘扩散函数 (edge spread function，ESF)，求取亚像素级的线扩散函数(line spread function，LSF)，并以LSF的参数σ作为清晰度评价值，不仅取得较高的对焦精度，而且自动对焦时间不超过0.2 s，由于σ对环境参数比较敏感，难以应用到多变的工业测量系统中。

针对复杂多变的工业测量现场，现代自动对焦算法从图像清晰度评价、焦点搜索和对环境的适应等几方面提出稳定性、准确性和抗干扰等要求。现有的清晰度评价函数往往易受光照、振动等因素的干扰，而搜索算法在清晰度评价值不理想的情况下易受局部峰值的影响而导致搜索失败。同时，搜索算法大多数是基于图像评价值的最大值位置来确定对焦位置，由于任何一种搜索算法都是按照一定步长进行搜索，所采集的图片是离散的。因此，图像评价值的最大值位置往往并不是最接近真实的对焦位置，即不是最优对焦位置。

本文提出一种应用于工业影像测量的自动对焦算法。首先，提出基于模糊熵对图像的不确定程度进行测量，并基于图像灰度差的统计分析对图像清晰度进行评价；然后，提出一种多尺度全局搜索和微尺寸曲线拟合相结合的搜索方法，多尺度全局搜索的目的是通过逐步缩小搜索区域和搜索步长，迅速搜索到清晰度评价值的最大值位置，而曲线拟合的目的是获取最优对焦位置而不是传统的基于图像评价值最大值位置的对焦位置；最后，将本文所提出的自动对焦算法在实际工业影像测量系统中进行验证。

1 基于模糊熵的清晰度评价函数

理想的自动对焦要求对焦评价函数具有单峰性、尖锐性和唯一性等特点。模糊逻辑的主要思想是把人类认识事物的经验法则转化为模糊理论所使用的模糊规则，对于模糊集合，由于不同人所用判断标准不同，因此，隶属度函数及各元素的隶属度也不尽相同。模糊熵的引入用于对模糊集的模糊程度进行合理度量[7]，可以很好地对系统的复杂性和不确定性进行描述。本文中，模糊熵被用于对图像的不确定程度进行测量，基于模糊熵的图像清晰度评价方法的具体实现过程如下。

步骤1 模糊熵的定义。

设m×n维图像具有N个灰度级，像素(i,j)的灰度级表示为f(i,j)，并进行归一化处理，以降低光照条件对清晰度评价的影响。定义模糊集A，其论域为图像的灰度级，并定义模糊集合的隶属度函数为

(1)

(1)式中：k为归一化处理后的像素灰度值；0.5≤μk(f(i,j))≤1。由(1)式可得，当f(i,j)=k，隶属度函数μk最大。对于图像清晰度评价，隶属度函数用于对像素(i,j)与其周围像素的灰度级差进行测量，灰度级差越小，则隶属程度越大，反之亦然。

在模糊集A上定义模糊熵为

(2)

由(2)式可知，当f(i,j)=k时，隶属度函数最大而模糊熵最小，且模糊熵在f(i,j)=k具有对称性。

步骤2 图像清晰度评价。

由于图像对比度与图像的清晰度密切相关，为了对图像清晰度进行评价，基于上面所定义的模糊熵对图像对比矩阵进行计算。以图像中每一个像素的灰度级构建m×n维矩阵M，在矩阵M中，取像素点(i,j)为中心，大小为l×l(l取为奇数，本文取l=3)的一个窗口。根据(1)式和(2) 式，如果像素点(i,j)和窗口内其他像素点的灰度级差小，则其隶属度值大而模糊熵值小。因此，基于模糊熵的图像对比评价值计算式为

(3)

当像素点(i,j)为边缘点时，窗口内各点的灰度级差异大，则mk(i,j)的值也较大。因此，图像对比评价值mk(i,j)随着像素点灰度级差的增大而单调增大。对图像中所有的像素点分别计算测度mk(i,j)，得到图像对比矩阵[mk(i,j)]m×n。

基于图像对比矩阵对图像清晰度进行测量。考虑到减小计算量、降低计算复杂性，将对焦窗口W内各点的计算图像对比评价值mk(i,j) 的和作为图像清晰度评价函数为

(4)

为了验证所提出的图像清晰度评价函数的应用效果，在理想光照条件和最优放大倍率下，对图1a所示的轴瓦进行下面的试验，图1b和图1c分别为轴瓦的正焦图片和离焦图片。固定CCD镜头到轴瓦的距离不变，以固定步长从远至近进行对焦，对不同聚焦状态的图片进行采集，并在其中心窗口截取320×320像素的对焦窗口，将所获取图片按照对焦状态进行排列。

图1 待检测工件Fig.1 Tested workpiece

图2为本文的清晰度评价函数与Roberts算子，Laplacian算子，Breener算子和Tenengrad算子[8]的清晰度评价值对比曲线，在所测试的清晰度评价函数中，只有本文的算法呈现单峰性，这将有利于后面对最优对焦位置的搜索，其他测试算法都呈现多个峰值点，难以对正焦位置做出正确的评价。

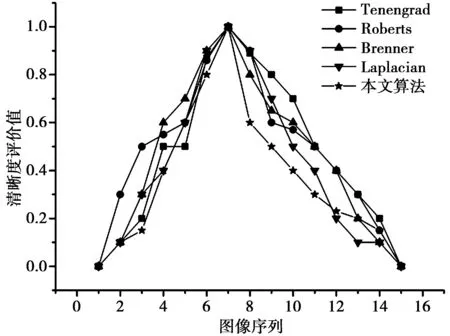
图2 清晰度评价函数值对比曲线Fig.2 Compared curve of different definition evaluations

2 最优搜索算法

现有大多数搜索算法均存在2个影响对焦精度的缺陷[9-10]：①当评价值曲线出现局部峰值，由于大多数搜索算法都不是基于全局搜素，容易陷入局部峰值而导致搜索失败；②即便是全局搜索，因为现有搜索算法多是基于最大评价值位置进行对焦，在获取图像的过程中，由于采集步长以及开始位置等的影响，所搜索到的对焦位置往往并不是最优的对焦位置。

为克服上述2个缺陷，本文提出一种全局搜索和微尺寸曲线拟合相结合的搜索算法。首先，多尺度全局搜索算法用于快速搜索清晰度评价值的最大值位置；然后，以最后一次全局搜索所获取的最大评价值位置为中心进行曲线拟合，所拟合曲线的峰值位置就是所搜索到的实际对焦位置。在组合搜索过程中，为了确保真实对焦位置一定在搜索区间内，搜索区间一定是以上一次的搜索顶点为中心并两端对称的。具体实现过程如下。

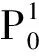
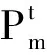
步骤4 假设最后一步全局搜索中所获取的最大评价值所在镜头位置为Pm，在最后一次搜索获取的清晰度评价值集合中，以Pm为中心位置，两侧各取相同数量的点，对这些点的评价值进行曲线拟合。拟合采用(5)式所示的二次多项式。

y=a+bx+cx2

(5)

(5)式中：x表示镜头搜索位置；y表示图像评价值。二次多项式的参数a，b和c由最小二乘法计算，如(6)式所示。

(6)

最后，拟合曲线的顶点Pf，即最优对焦的实际对焦位置为

(7)

针对图1所示轴瓦，对最优搜索算法进行验证。试验前，将CCD的真实对焦位置设置在26.12 mm处，改变系统光照和放大倍率，使清晰度评价曲线出现局部峰值，如图3a所示。图3b和图3c分别给出了改进搜索算法的中间搜索过程和最终搜索结果，图3中P1，P2和P3分别是第1次、第2次和第3次全局搜索所得到的最大清晰度评价值位置，P4是曲线拟合所得到的曲线顶点即实际的对焦位置，P所在的直线表示真实对焦位置。

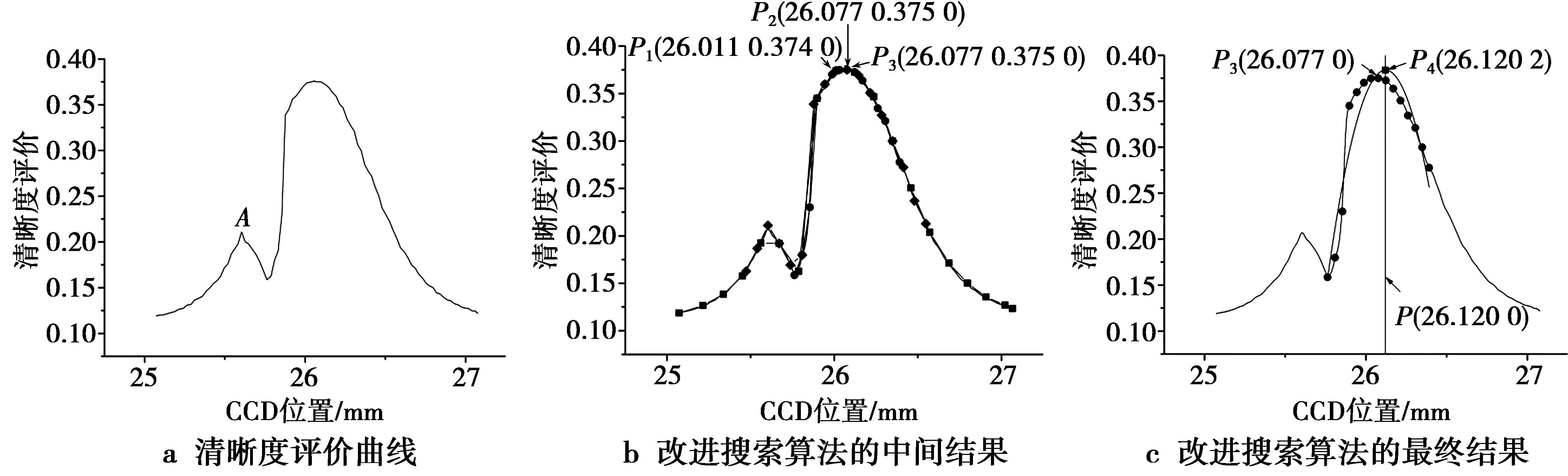
图3 改进搜索算法的搜索过程Fig.3 Searching process of improved search method

由图3可知，本文所提出的最优搜索算法能够避免局部峰值的干扰搜索到正确的对焦位置。此外，多尺度全局搜索，逐步缩小搜索区间和搜索步长，搜索到的最大评价值所在镜头位置也逐步接近真实对焦位置。但是，这个位置容易受到搜索起始位置和搜索步长的影响，很难搜索到最接近真实对焦位置的最优对焦位置。在多尺度全局搜索的基础上增加微尺寸曲线拟合，对起始搜索位置和搜索步长具有更强的鲁棒性，并能够提高自动对焦的精度和稳定性，通过和真实聚焦位置的距离比较(|P-P3|>|P-P4|)，说明经过拟合后得到的聚焦位置要更接近真实的聚焦位置。

3 自动对焦试验及分析

为了验证所提出自动对焦算法的有效性，进行了工件自动测高试验，如图4所示。试验对象是图4a所示刹车片，图4中小圈所示为对焦位置，图4b和图4c分别为刹车片的正焦图片和离焦图片。刹车片的真实高度为67.56 mm。理论上，图像最清晰的位置所测到的工件高度是最准确的。

本文所用测试系统框图如图5所示，包括电脑8分区程控LED光源；高清晰彩色摄像机，采用连续变焦镜头；高精度精密级封闭式光栅尺，分辨率为1 μm；传动系统采用高精密无牙光杠，由伺服电机驱动；导轨为精密P级线性导轨。系统的工作过程如下：①设置镜头放大倍率和光照强度，采集图像；②计算图像评价值，搜索对焦位置；③驱动电机至对焦位置并采集图像用于工件尺寸测量；④对图像进行处理并计算工件的尺寸；⑤程序修正光栅尺误差和垂直误差等，然后记录测量结果。

图4 试验对象Fig.4 Tested object

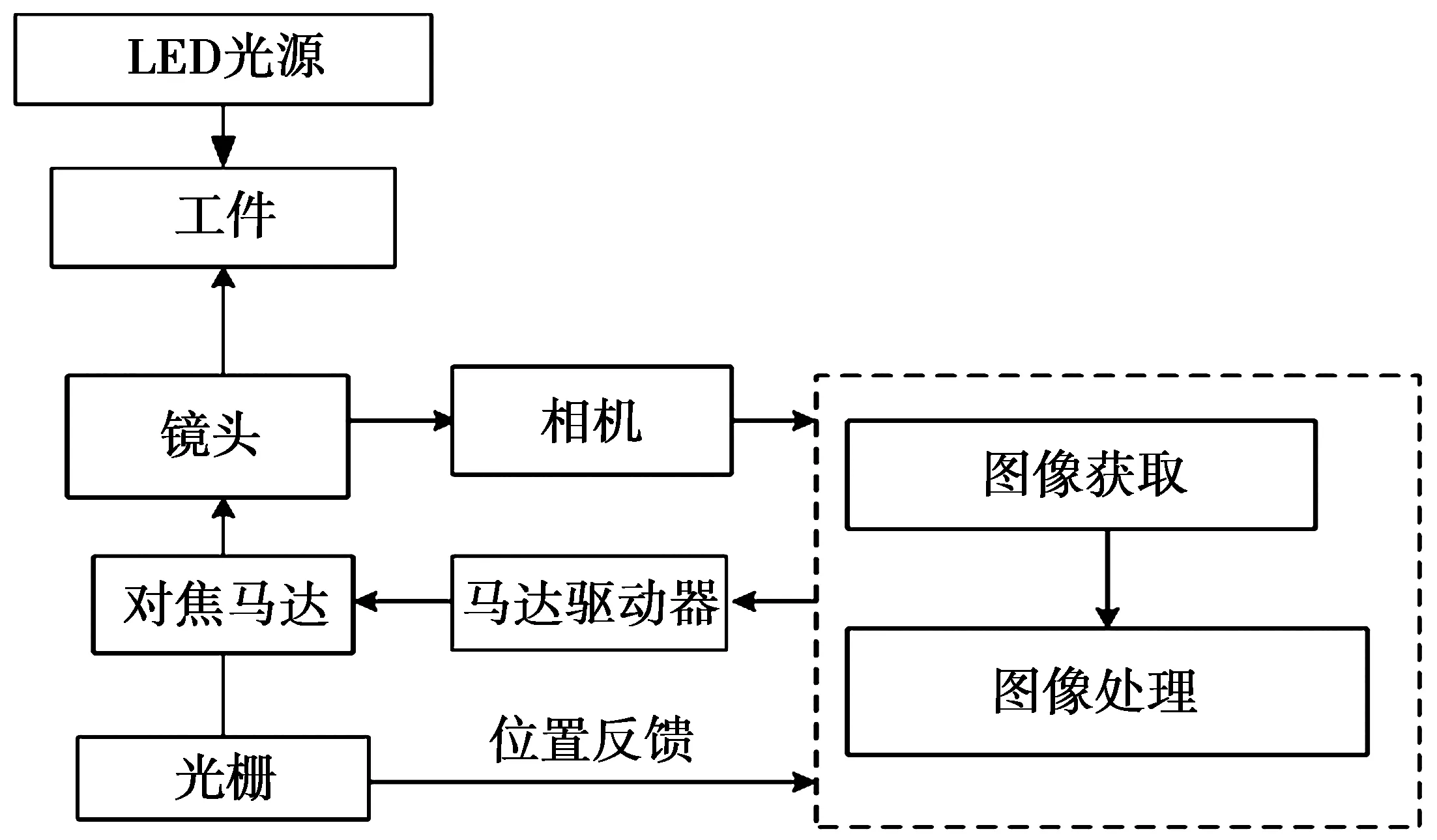
图5 影像测量系统框图Fig.5 Diagram of the image based measurement system

工业影像测量系统中，精度、重复性和稳定性是评价系统实际应用效果的3个重要性能。设{p1,p2,…,pn}为一系列试验所得到的工件测量高度值，均方根误差(root mean square error，RMSE)用于对精度进行评价，表示为

RMSE=

(8)

(8)式中，p0表示工件真实高度值。均方根误差越小，则对焦精度越高。

标准差(standard deviation，SD)用于对重复性进行评价，表示为

(9)

(9)式中，μ表示测量高度值{p1,p2,…,pn}的平均值，标准差越小，则对焦重复性越高。

公差(tolerance，T)用于对稳定性进行评价，表示为

(10)

公差越小，则对焦稳定性越好。

实际影像测量系统中，图像自动对焦很容易受到环境因素特别是噪声、放大倍率和光照强度的影响。对本文所提出的自动对焦算法和文献[5,11]中的自动对焦算法进行对比试验，包括最佳放大倍率和最佳光强指数条件下的试验，放大倍率变化，光强指数变化条件下的试验。文献[5,11]中的自动对焦算法分别用AF1和AF2表示，本文所提出的自动对焦算法用AF3表示。

3.1 最佳放大倍率和光照强度条件下的测高试验

在本文系统中，最佳镜头放大倍率为3，对应的最佳光强指数为35。对用于比较的自动对焦算法(AF1，AF2和AF3)分别进行10次测高试验，图6为对比算法的计算均方根误差、均方差和公差，相比较其他3种自动对焦算法，本文所提出的自动对焦算法(AF3)不仅有更高的对焦精度(较小的RMSE)，而且具有更好的重复性和稳定性(较小的SD和T)。

3.2 放大倍率变化条件下的测高试验

在实际系统中，放大倍率和光照强度经常由于噪声和振动等的影响而发生变化，进而对自动对焦的性能发生影响。试验中，放大倍率从2.5增加到3.5，每次试验增加0.1，而光强指数固定在35不变。试验的每个对焦算法在每个放大倍率下各进行一次试验，图7为对比算法的计算均方根误差、均方差和公差。其他3种自动对焦算法的3个指标值均有所增大，表示算法性能变差，而本文的自动对焦算法(AF3)仍然保持高的对焦精度(即较小的RMSE)、好的重复性和稳定性(较小的SD和T)。

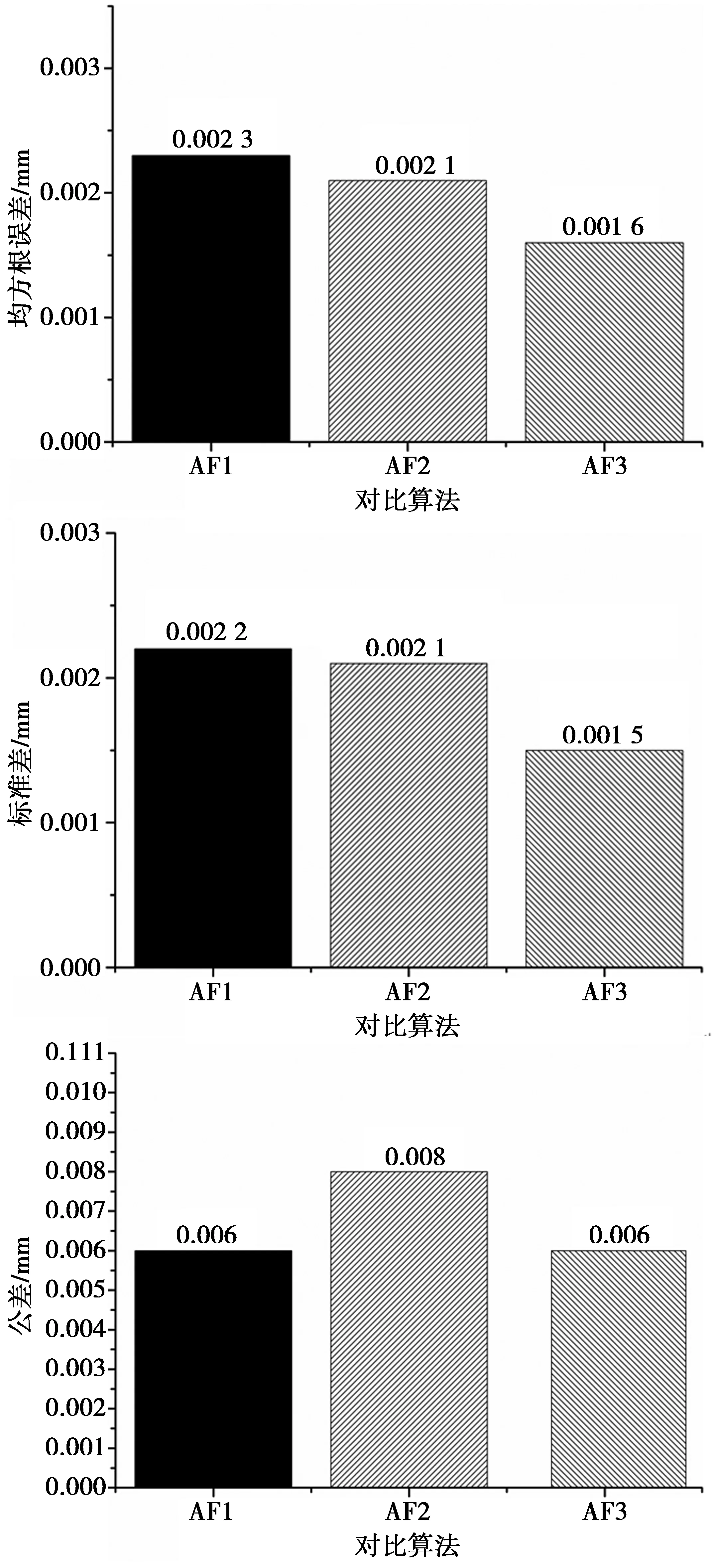
图6 理想试验条件下不同自动对焦算法性能对比Fig.6 Compared results of different auto-focusing algorithms under ideal test condition

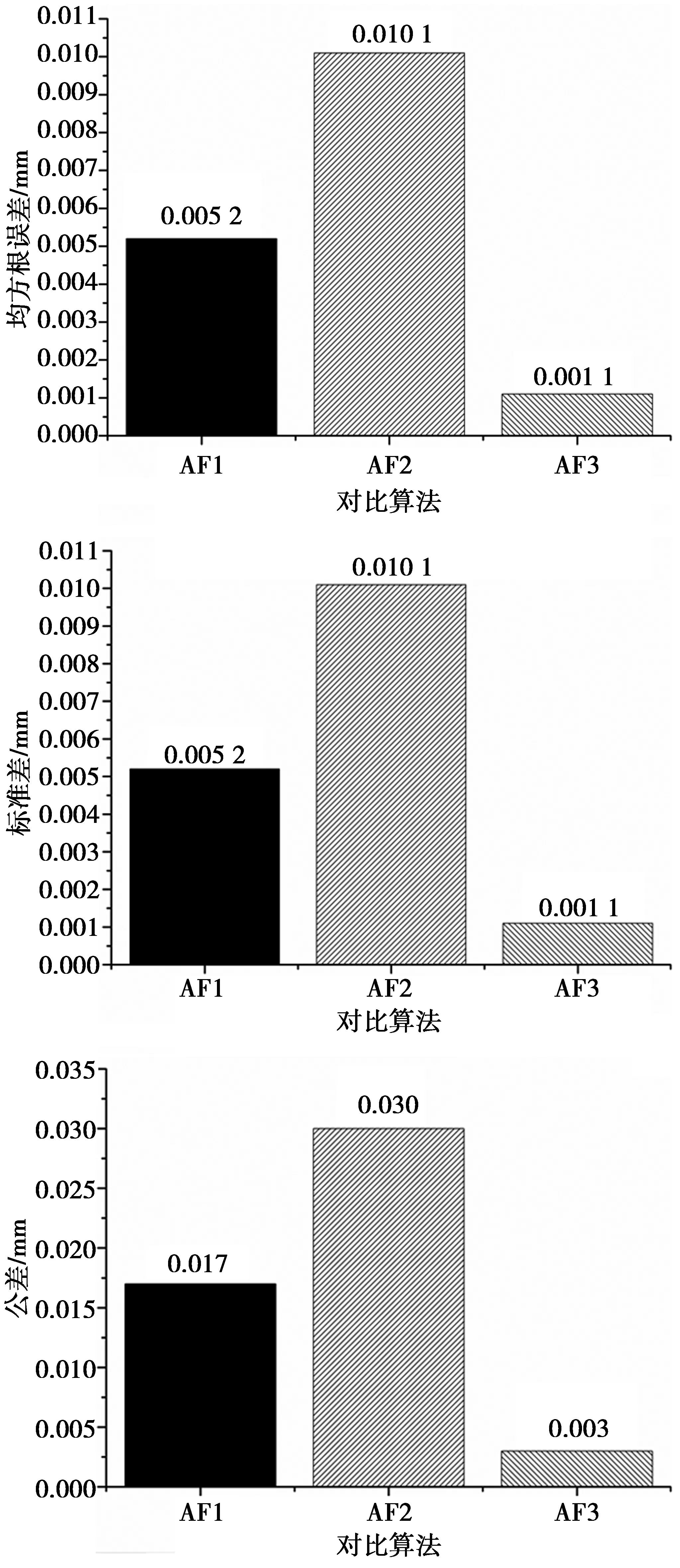
图7 放大倍率变化条件下不同自动对焦算法性能对比Fig.7 Compared results of different auto-focusing algorithms under amplification change condition

3.3 光照强度变化条件下的测高试验

试验中，光强指数从30增加到40，每次试验增加1，而放大倍率固定在3不变。试验的每个对焦算法在每个光照强度下各进行一次试验。同样地，各对比算法的计算均方根误差、均方差和公差如图8所示，其他3种自动对焦算法3个指标值均增大，算法性能变差，而本文所提出的自动对焦算法(AF3)仍然具有良好的性能。

本文所提出的自动对焦算法不仅有很高的精度，而且有很好的重复性和稳定性，对于放大倍率和光照强度的变化具有很好的鲁棒性，有利于满足复杂环境下的工业影像测量。

4 结束语

本文提出了一种图像自动对焦算法。首先，模糊熵被用于对复杂图像处理进行建模和对图像清晰度进行评价；然后，提出了多尺度全局搜索结合微尺寸曲线拟合的最优对焦搜索算法，能够实现高精度的最优对焦；最后，对比试验结果表明，该自动对焦算法不仅具有很高的对焦精度，而且在放大倍率和光照强度变化下具有很好的重复性和稳定性。该算法能够满足工业测量及其他复杂测试环境对自动对焦系统的要求。

[1] MOSCARITOLO M, JAMPEL H, KNEZEVICH F, et al. An image based auto-focusing algorithm for digital fundus photography [J]. IEEE Transactions on Medical Imaging, 2009, 28(11): 1703-1707.

[2] REDONDO R, BUENO G, VALDIVIEZE J C, et al.Autofocus evaluation for brightfield microscopy pathology[J].Journal of Biomedical Optics,2012，17(3): 99-106.

[3] AKIYAMA A, KOBAYASHI N, MUTOH E, et al. Infrared image guidance for ground vehicle based on fast wavelet image focusing and tracking[C]//Proceedings of SPIE.Bellingham USA：SPIE，2009: 1-8.

[4] GAMADIA M, KEHTARNAVAZ N，HOFFMAN K R.Low-light auto-focus enhancement for digital and cell-phone camera image pipelines[J].IEEE Transactions on Consumer Electronic,2007,53(2): 249-257.

[5] LIU Chuntong,HE Zhenxin,ZHAN Ying,et al. Searching algorithm of theodolite auto-focusing based on compound focal judgment[J].EURASIP Journal on Wireless Communications and Networking,2014(1)：1-11.

[6] 卢振华,郭永飞,李洪法，等.利用LSF实现推扫式遥感相机的自动调焦[J]. 红外与激光工程, 2012, 41(7):1808-1814. LU Zhenhua,GUO Yongfei,LI Hongfa,et al.Auto-focus using LSF in aerial push-broom remote-sensing camera[J].Infrared and Laser Engineering,2012,41(7):1808-1814.

[7] ALSHARHAN S, KARRAY F, GUEAIEB W, et al. Fuzzy entropy: a brief survey[C]//IEEE.2001 IEEE International Fuzzy Systems Conference.New York:IEEE Press,1135-1139.

[8] 王健, 陈洪斌, 周国忠, 等. 改进的Brenner图像清晰度评价算法[J].光子学报,2012, 41(7):855-858. WANG Jian, CHEN Hongbin, ZHOU Guozhong, et al. An improved brenner algorithm for image definition criterion[J].Acta Photonica Sinica,2012,41(7):855-858.

[9] GAMADIA M,KEHTARNAVAZ N.A filter-switching auto-focus framework for consumer camera imaging systems [J].IEEE Transactions on Consumer Electronics, 2012, 58(2):228-236.

[10] MOSCARITOLO M, JAMPEL H, KNEZEVICH F, et al. An image based auto-focusing algorithm for digital fundus photography [J]. IEEE Transactions on medical imaging, 2009, 28(11):1703-1707.

[11] FLORIAN D, KOCK H, PLANKENSTEINER K, et al. Auto focus and image registration techniques for infrared imaging of microelectronic devices[J].Measurement Science & Technology, 2013(24): 1-11.

(编辑：王敏琦)

The National Natural Science Foundation of China(61375112)

Aimed at problems of the traditional auto-focusing algorithms，such as the optimal focusing achievement, the local peaks of definition evaluation function influence, this paper presents an image auto-focusing algorithm for industrial image measurement. Firstly, a new image definition evaluation method based on the fuzzy entropy is applied, which can reduce negative influences of noise and variations of lens magnification and light intensity. Secondly, a search method combined the multi-scale global search and fine-level curve fitting is proposed, which can avoid the interference of the local peaks and achieve the best image focus. The proposed image auto-focusing algorithm has the advantages of high focusing accuracy, high repeatability and stability under the variations of lens magnification and light intensity, which make it applicable for the industrial image measurement. Experimental results and comparisons on the practical industrial image measurement system have been presented to show the effectiveness and superiority of the proposed algorithm.

auto-focusing; fuzzy entropy; definition evaluation; global search; curve fitting; optimal focusing

10.3979/j.issn.1673-825X.2017.04.014

2016-07-22

2016-12-19 通讯作者：刘书炘 liushuxin01@163.com

国家自然科学基金(61375112)

TP391.4

A

1673-825X(2017)04-0514-07

Auto-focusing algorithm based on fuzzy entropy evaluation andoptimal search

(1.School of Educational Science, Minnan Normal University, Zhangzhou 363000, P.R. China;2.School of EIEE, Shanghai Jiao Tong University, Shanghai 200240, P.R. China)

刘书炘(1977-)，男，福建漳州人，讲师，主要研究方向为数字图像处理、计算机视觉。E-mail: liushuxin01@163.com。 刘满华(1975-)，女，上海人，副教授，主要研究方向为生物特征识别、模式识别与机器学习、计算机视觉。E-mail: mhliu@sjtu.edu.cn。

LIU Shuxin1, LIU Manhua2