基于电子看板的装配线物料配送优化研究
韩曙光,蒋欢欢,胡觉亮
(浙江理工大学,a.理学院;b.经济管理学院,杭州 310018)
基于电子看板的装配线物料配送优化研究
韩曙光a,蒋欢欢b,胡觉亮a
(浙江理工大学,a.理学院;b.经济管理学院,杭州 310018)
针对在使用电子看板拉动式环境下,机械产品装配线停线待料,线边物料堆积,配送成本高等问题,以总成本最小为优化目标,综合考虑看板消耗速度参差不齐,线边容量有限,生产线发送需求时间的不确定性和需求量确定性等特点,建立可分割式物料配送模型。以S公司电动工具装配线为例,应用所建立的数学模型,利用Lingo编程求解并给出具体配送方案,且通过与传统循环配送方案的对比结果证明了该模型的可行性及有效性。最后,物料看板数量的调整结果表明线边最高库存量是随看板数量和拣货时间的增加而不断的增长,决策者可以根据实际线边库存容量选择合适的拣货时间和物料看板数量来优化总成本。
电子看板;精益生产物流;物料配送;线边库存
随着经济的全球化,制造行业由以前的局部竞争演变到如今全球范围内的激烈竞争[1],这迫使国内的一些制造企业苦练内功,摒弃传统粗广式的生产转向适应多样化市场需求的个性化生产。而精益生产以满足客户个性化需求为目标,不断消除浪费,挖掘收益,赢得了企业管理者的青睐[2]。装配是机械生产过程中必不可少的一部分,且其涉及众多的物料、半成品再加上生产线线边库存面积有限,这给物料管理和物料配送增加了难度[3-5]。因此高效的物料配送系统是保证装配线柔性和提高生产效率的关键支柱[6]。然而在实际生产活动中,配送人员往往根据自己的经验判断是否该进行物料的配送及配送次数,所以经常出现停线待料、生产线线边物料堆积严重、配送设备闲置等现象,这已经成为促进进一步实施精益生产的重要障碍。因此装配线的物料配送问题引起了众多学者的关注。
洪旭东等[7]研究了在传统看板环境下物料循环配送模式,并提出其配送系统是在一个确定的时间段完成的,因此是一个定期订货的过程;蒋丽等[8]提出以工位为配送对象,以配送总时间最短为目标的车辆调度模型;Boysen等[9]以工位旁最高库存量最小为目标建立准时制物料配送模型,运用模拟退火算法对其进行求解;葛茂根等[10]研究了主动式物料配送,实现了多条生产线多工位多零件的实时、小批量配送; Donati等[11]研究了客户对时间依赖程度不同的车辆路径问题;李晋航[12]以提高车辆满载率为目标,考虑车辆容量和服务时间等约束下的物料配送路径问题;党立伟等[13]根据制造BOM 和装配工艺流程,求得其最优配送周期和每次配送量;刘明周等[14]研究了不确定环境下的混流装配线物料配送问题,构建了基于射频识别技术的物料配送控制系统;丁佳琪等[15]以成本最小为目标,考虑线边库存容量和牵引车最大运输量约束,寻求出最优循环周期和看板数量。
对于物料配送的相关研究,大多数是在传统看板环境下,以多条产线,单一产品,单一物料为对象,研究其在不停线的情况下考虑各种因素后求得循环配送的最佳配送周期及看板数量,或变拉动式为主动式的物料配送模式以降低运输总成本等。而目前一些优秀的制造企业已使用电子看板代替了传统的手动看板[16-17],仓库与生产线信息的传递由传统的收取纸质看板转变为领料电子信号。电子看板环境下的循环配送,是在仓库收集到物料员发送的需求信息后,将物料放置在小车内,牵引车以一定的周期装载小车循环配送至生产线的方式,其对物料员发送需求准确性依赖较强。而实际生产中,装配线柔性化程度高,生产换型较频繁,装配零部件繁多,各物料看板可消耗时间参差不齐,必然会发生因发送需求时间的延误或提前而导致的生产线缺料和堆积。因此本文提出在接收到生产线领料信息后,综合考虑线边库存面积有限、物料消耗速度参差不齐等特点,建立总成本最小可分割式物料配送模型,指导仓储部门进行物料的配送,降低人为因素导致的停线和物料堆积。
一、电子看板环境下的生产线物料配送
看板是用来表示某生产线的某个工位需要某种物料数量的卡片。电子看板,是将信息技术应用于生产可视化的一种工具[17]。生产线利用扫描设备自动识别看板卡上的信息,并通过信息网络直接将领料信息传递给仓库,仓库再根据信息拣货、配送。电子看板改变了传统的实物看板的投递和统计的过程,避免了实物看板在传递过程中的丢失、涂改和损坏,也增加了信息的及时性和可靠性。
在电子看板环境下仓库进行物料配送的流程:仓库接收生产线需求信息,打印拣货单—拣货—配送—回到仓库。整个流程见图1。
图1所示的流程图触发点在于生产线发出物料需求信号,配送流程以回到仓库为起点和终点。生产线通过电子看板将领料需求信号传递给仓库;仓库管理人员每隔一段时间处理并打印各生产线的领料请求,即生成拣货单;拣货员根据拣货单信息分别去物料超市和仓库拣货,拣货完毕后装入小车;当到配送时间时,配送人员出发,按照已经安排好的路线到达生产线,若该生产线有已定物料则卸载该小车,若无,则是否有空小车,若有,则装载;继续行驶至生产线,最后回到仓库,将空车交付于管理员,物料配送结束。
传统看板环境下,物料员每次从线旁物料架取走物料并将领料看板放入该周转箱,发出物料需求信息。虽然发送需求信息的时间不固定,但是配送人员却按固定的周期到达生产线,收取看板和料盒并送货,是一个定期订货的模式。但电子看板环境下,由于物料员发送物料需求时间不规律性,因此仓库无法在固定的周期内处理订单信息时接收到该生产线该物料的需求信息,但是可根据收集到的物料需求信息,按需实施分车次配送,例如,仓库收到的领料信息清单中,某些工位线边已堆积,则仓库可另外安排车次进行配送,以此来减少线边物料的堆积。
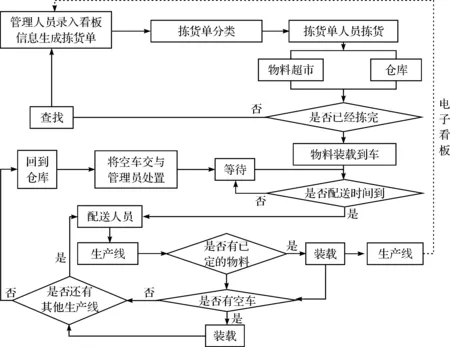
图1 基于电子看板的生产线物料配送流程
二、物料配送模型
(一)问题描述
在电子看板环境下的生产线物料配送过程中,仓库先由生产计划获知产品型号与数量,物料员通过电子看板将领料需求信息发送给仓库,仓库根据看板信息读出物料需求数量,所在工位,产品的节拍,每个产品所需物料的数量,上一次物料配送的时间及配送后线边的库存量,然后决定配送该物料的时间,保证生产线不会缺料和避免堆积。假设:
a)文中所研究的物料配送指的是车间内部物料的流动,将物料从仓库的缓存区配送到所需生产线或工位,并不包括场外的一切物料配送活动。其中生产线各间距较短,牵引车行驶时间可忽略不计;
b)为确保生产及配送的可持续,物料超市及仓库缓存区不缺货;
c)每条生产线有多个工位,可生产多种产品,但某一时刻生产线只能生产一种产品,仓库接收的领料信号都一一对应某个产品,某个生产线和某个工位;
d)为节省拆包成本和防止零部件因拆包而引起氧化或损坏,采用原包装上料,看板的数量为物料原包装的数量;
e)生产线按生产计划规定的节拍生产,没有出现设备故障损坏等等;
f)每辆牵引车的配送范围和生产线的数量已经确定,且一次配送可满足该范围内所有生产线工位的物料需求;
g)多条生产线多工位可同时发出领料需求,仓库每隔一段时间处理此间隔期内的所有领料需求;
h)不考虑因配送物料的数量引起的成本,只考虑车辆的启动成本。
(二)符号说明
i——零件的种类;
j——工位号;
k——配送的次数;
l——仓库处理订单的时刻;
h——仓库拣货的平均时间;
h1——车辆到达工位的平均时间;
c——总成本;
Oij——j工位i零件的线边库存量;
tij——j工位i零件的生产节拍;
μij——j工位i零件的系数;
C——一个标准零件的线边库存成本;
a(k)——第k次车辆启动成本;


Nij——j工位i零件的看板数量;

T(k)——第k次车辆配送的时刻。
(三)配送模型
为降低线边最高库存量的同时降低物料配送成本,因此以总成本最小为优化目标,构建可分割式物料配送模型:
(1)
(2)
(3)
(4)
(5)
(6)

i=1,2,…,n,j=1,2,…,m,k=1,2,…,s.
式(1)为目标函数,最高线边库存成本与配送成本之和最小;式(2)为第k次配送完零件的线边库存量;式(3)表示第k次是否启动车辆配送;式(4)表示发送一次领料需求后,该物料只能被配送一次,且配送数量为看板数量;式(6)和式(7)分别表示第1次配送或第k次配送的时间必须大于发出领料需求时间、拣货时间和配送时间之和,且小于或等于最先消耗完的零件时间。
(四)模型结果集
模型的结果集是关于车次、车辆配送时刻、配送零件的种类及数量、所至工位的集合,因此可表示为:
(8)
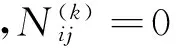
三、算例分析
以S电动工具公司厂内物料配送系统为例验证本文所述的可分割式物料配送方案,仓库每5分钟处理一次生产线的物料需求,表1是某日上午仓库接收到的来自生产线的物料需求,在现有的人力资源下需要15分钟才能完成拣货,车辆的启动成本为2元/次,其到达工位的时间很短,可忽略不计,一个标准零件的线边库存成本为2元/分钟。
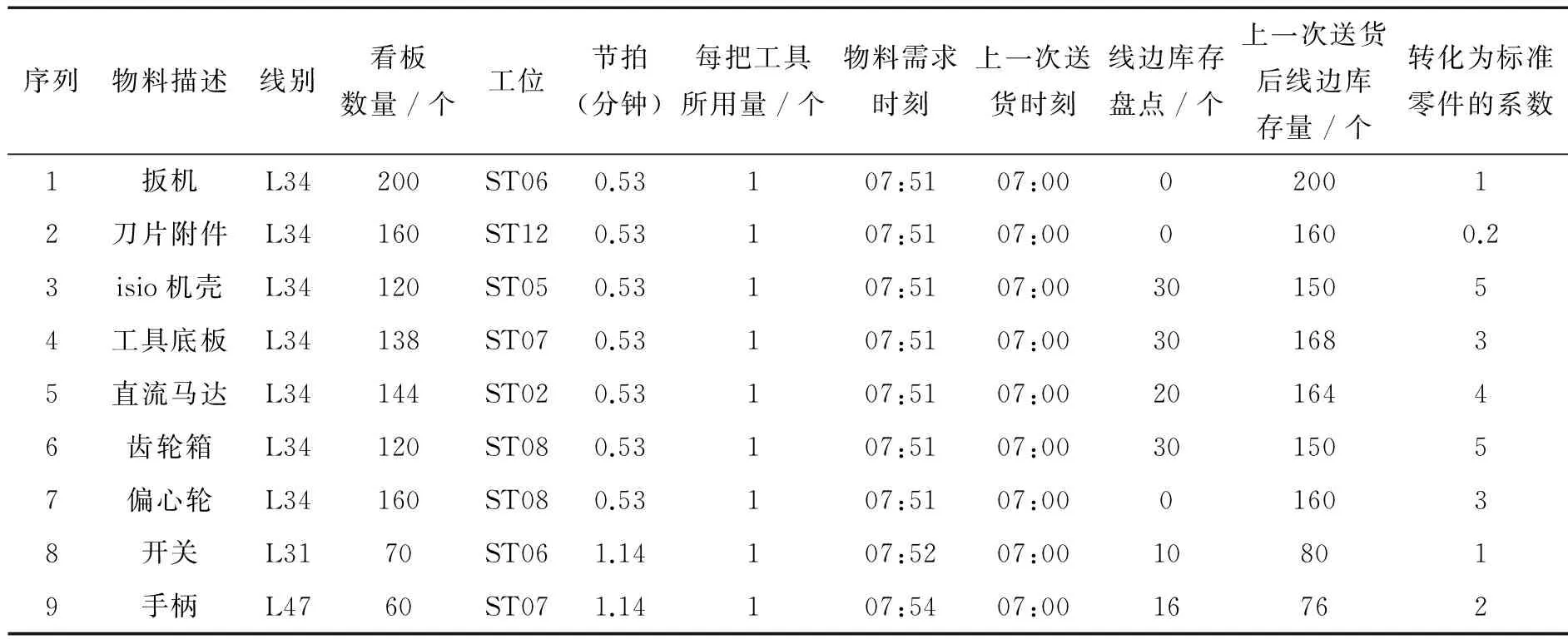
表1 仓库接收到的生产线物料需求信息
结合以上数据和已建立可分割式配送模型可得:l=7:55,h=15,h1=0 ,

C=2,a(k)=2,k=1,2,…s.
然后利用Lingo编程求解得s=4,c=6667.18,配送方案结果集为:

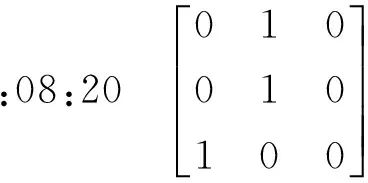
(9)


(10)
式(9)表示第一次配送的时刻为08:15,配送isio机壳、齿轮箱;第二次配送的时刻为08:20,配送刀片附件、直流马达、偏心轮;式(10)表示第三次配送的时刻为08:24,配送工具底板、开关;第四次配送的时刻为08:36,配送扳机、手柄。
S公司曾分别采用过5分钟循环式配送与30分钟循环式配送这两种配送模式进行物料的配送,在这两种模式下具体配送方案如表2所示。图2为可分割式配送方案,5分钟循环式配送方案与30分钟循环式配送方案下的各物料最高线边库存量对比图,表3为这三种配送方案的停线时间的统计表。从表2、图2和表3中可知,30分钟循环式配送方案虽然最高线边库存量和总成本最低,但是停线时间最长,这就意味着生产线的物料需求得不到满足,生产效率下降,时间浪费多,并且很有可能影响公司在计划时间范围内交付产品,其停线损失成本是不可估量的,因此若决策者要求保证生产线不停线的条件下以总成本最小为目标,则可分割式的配送方案显然优于其他两个方案;若从仓库运营管理的角度看,5分钟与30分钟循环一次的配送方案管理难度低于可分割式配送,因为前两者不需仓库在配送前计算各物料的配送时刻,只需进行周期式的循环配送就可以,但30分钟循环式配送停线时间较多,因此5分钟循环配送方案会是仓库管理者最佳选择的配送方案;若以最高线边库存量为优化目标即生产线边面积较小为决策重点,且允许一定时间的停线,则30分钟循环一次配送方案为最优配送方案。

表2 5分钟与30分钟循环式配送方案

图2 不同配送方案的最高线边库存量的对比

表3 不同配送方案的停线时间 分钟
从图2中可看出,可分割式配送方案的最高线边库存量低于5分钟循环式配送方案,分析其原因发现,表1中生产线发送的物料需求数量即看板数量可消耗时间参差不齐,5分钟循环式配送只是按照周期进行配送,不考虑各物料的消耗情况,而可分割式配送模式中物料的配送时间是根据各物料积压线边库存量的消耗时间的不同来决定的,因此在保证生产线不停线的情况下,可分割式配送方案的最高线边库存量必然低于周期式的配送方案。

表4为看板数量调整前与调整后分别采用分割式配送的最高线边库存量统计表,从表4中的数据计算可得调整前平均线边最高库存量为140个,调整后平均线边最高库存量为59个。相较于看板数量调整前,调整后的最高线边库存量平均下降了58%,同时通过对调整前后总成本的比较发现,看板数量调整后总成本下降了55%。究其原因,平均看板数量相较于调整前的数量降低了68%,且看板可消耗时间一致,因此,在可分割式配送模式下,各物料看板消耗时间为常数值时,线边最高平均库存量和总成本会随看板数量下降而下降。

表4 看板数量调整前后最高线边库存量统计表 个
由看板的数量计算公式可知,看板数量与波动时间和拣货时间有关。然而在一段时期内,车间内生产物流的波动时间不会变,那么看板数量就与补货时间有很强的关联性,补货时间越长,看板数越大,则线边最高库存量越高,相应的线边占地面积也会越大,因此补货时间越短越好。然而补货时间的缩短与仓库投入的拣货成本有关,成本越高,补货时间越短,在这相互制衡的作用下可得到补货时间h与总成本c′(运输成本,线边最高库存成本与补货成本之和)的关系如图3所示。若线边面积为S时,h=h0,C′=C0,从图3中发现若线边面积最大库存量可大于等于S,则h=h0时总成本最小;若线边面积较小,线边最大库存量必须小于S时,则当h=h1时,总成本为最小,因此仓库决策者可根据线边面积来决定拣货投入的成本与看板数量。

图3 拣货时间与总成本的关系
四、结 语
分析了使用电子看板环境下生产线物料配送流程,建立了物料配送模型,变循环周期式配送为分割式配送,实现了物料灵活、及时、准确的配送。以S公司电动工具装配线为例,利用Lingo计算结果来指导仓库的物料配送,并通过与循环配送的对比结果验证了模型的可行性,并指出线边的最高库存量和看板数量受拣货时间影响,决策者可根据线边库存面积来决策仓库拣货时间和看板数量,进一步提高资源的利用率和物料配送效率,降低生产物流成本。但是目前物料配送都是靠经验来进行,缺乏系统的软件和硬件的支持。为了不断追求精益生产中“点库存”和“一个流”的高效生产车间,未来可将生产线成品转运与物料配送相结合,构建生产现场信息与配送系统信息实时交互系统,实现生产可视化,配送信息化及绿色化。
[1] 张伟.基于资源需求分析的准时生产工厂物流优化研究[D].上海:上海交通大学,2011.
[2] 陆君伟.精益生产实施流程与细化工具[M].北京:人民邮电出版社,2009.
[3] HANSON R, BROLIN A. A comparison of kitting and continuous supply in in-plant materials supply[J]. International Journal of Production Research, 2013,51(4):979-992.
[4] 常晓娥.面向混流装配线的精益物料配送方法研究[D].北京:北京交通大学,2015.
[5] GOLZ J, GUJJULA R, GUNTHER H. Part feeding at high-variant mixed-model assembly lines [J]. Flexible Services and Manufacturing Journal,2012,24(2):119-141.
[6] EMDE S, BOYSEN N. Optimally routing and scheduling tow trains for JIT-supply of mixed-model assembly lines [J]. European Journal of Operational Research,2012,217(2):287-299.
[7] 洪旭东,徐克林,夏天.基于看板的生产线物料循环配送方式[J].工业工程,2009,12(4):116-210.
[8] 蒋丽,丁斌,臧晓宁.以工位为中心的生产物流配送优化[J].计算机集成制造系统,2009,15(11):116-210.
[9] BOYSEN N, BOCK S. Scheduling just-in-time part supply for mixed-model assembly lines Original Research[J]. European Journal of Operational Research,2011,211(1):15-25.
[10] 葛茂根,刘明周,钱芳,等.基于JIT的多目标总装准时物料配送方法研究[J].中国机械工程,2011,22(23):2834-2838.
[11] DONATI V A, MONTEMANNI R, CASAGRANDE N, et al. Time dependent vehicle routing problem with a multi ant colony system [J]. European Journal of Operational Research,2008,185(3):1174-1191.
[12] 李晋航.混流制造车间物料配送调度优化研究[D].上海:华中科技大学,2012.
[13] 党立伟,孙小明.基于配送BOM的装配线物料循环准时化配送研究[J].机械制造,2012,50(7):89-91.
[14] 刘明周,王小巧,张铭鑫,等.不确定环境下混流装配线动态准时制物料配送系统[J].计算机集成制造系统,2014,20(12):3020-3029.
[15] 丁佳祺,张镓,蔡三发.基于看板的汽车生产物流超市物料配送优化研[J].物流技术,2015,34(10):225-227.
[16] MAURIAIO F, MAURO G, ALESSANDRO P. Kanban number optimization in a supermarket warehouse feeding a mixed-model assembly system[J]. International Journal of Production Research,2013,51(10):2997-3017.
[17] 方轩.电子看板在企业物流中的应用[D].上海:上海交通大学,2009.
(责任编辑: 陈和榜)
Research on Optimizing Material Distribution for Assembly Line Based on E-Kanban
HANShuguanga,JIANGHuanhuanb,HUJuelianga
(a.School of Science, Zhejiang Sci-Tech University;b.School of Economics and Management,Zhejiang Sci-Tech University, Hangzhou 310018, China)
Aiming at the lack of materials, heavy stock near-line and high delivery cost problems during the assembly process of mechanical products in the environment of using E-Kanban system, the split material distribution model was established to minimize total cost. The model comprehensively considered uneven consumption rate of Kanban, on-line capacity, uncertain material delivery time and fixed quantity required etc. This paper took assembly line of power tools for example, applied the mathematical model and Lingo programming to work out the specific distribution scheme. In addition, the comparison result with traditional cyclic distribution scheme proves the feasibility and effectiveness of this model. Finally, the result of Kanban quantity adjustment indicates that the highest near-line inventory increases with the increase of number of Kanban and picking time, and the decision-makers can choose appropriate time and quantity to optimize overall cost.
E-Kanban; lean production logistics; materials distribution; storage near-line
10.3969/j.issn.1673-3851.2017.04.005
2016-08-06 网络出版日期:2017-01-03
国家自然科学基金项目(11471286)
韩曙光(1977-),男,江苏建湖人,副教授,博士,主要从事供应链管理与优化、算法设计与分析方面的研究。
F224.9
A
1673- 3851 (2017) 02- 0120- 07

