冲击波作用下单层钢化玻璃抗爆性能的数值模拟研究
刘俊, 田宙, 钟巍,3, 谢淑红
(1.湘潭大学 材料科学与工程学院, 湖南 湘潭 411105; 2.西北核技术研究所, 陕西 西安 710024; 3.北京大学 数学科学学院, 北京 100871)
冲击波作用下单层钢化玻璃抗爆性能的数值模拟研究
刘俊1, 田宙2, 钟巍2,3, 谢淑红1
(1.湘潭大学 材料科学与工程学院, 湖南 湘潭 411105; 2.西北核技术研究所, 陕西 西安 710024; 3.北京大学 数学科学学院, 北京 100871)
借助通用显式动力分析程序LS-DYNA软件平台,采用拉格朗日方法描述钢化玻璃,增加侵蚀算法来模拟钢化玻璃的破坏。钢化玻璃采用线弹性材料模型,通过建立的模型研究单层钢化玻璃在爆炸冲击波作用下的动态响应。利用场地试验结果对数值模型进行验证,证明了此模型的合理性。用已验证的模型对单层钢化玻璃在爆炸冲击波作用下进行数值模拟,得到一组单层钢化玻璃破坏的超压冲量临界点。通过数值模拟结果得到了爆炸冲击波对单层钢化玻璃损伤的超压- 冲量曲线,进一步推导出了单层钢化玻璃损伤超压- 冲量曲线的经验公式,并与数值结果进行比对,具有很好的吻合性。研究表明,得到的超压- 冲量曲线及经验公式可以为单层钢化玻璃抗爆设计提供有价值的参考。
爆炸力学; 单层钢化玻璃; 数值模拟; 超压- 冲量曲线
0 引言
近年来,国内外报道的偶然爆炸和事故爆炸事件呈现上升趋势,针对公共建筑的恐怖爆炸袭击事件也时有发生。钢化玻璃作为现代建筑中采用最广泛的玻璃之一,在爆炸冲击波作用下易于破碎,进而可能会对人身和财物造成重大的损伤。因此,掌握冲击波作用下钢化玻璃的抗爆性能[1]可以有效地减少由于钢化玻璃破坏所造成的人身伤亡和财物损失。随着数值模拟技术的不断发展,数值模拟技术在爆炸冲击波对结构响应领域[2-3]发挥着越来越重要的作用。利用数值模拟方法来研究玻璃的抗爆性能近年来也取得了一些成果。Larcher等[4-5]通过试验与数值模拟相结合的方法,研究了夹层钢化玻璃在爆炸载荷下的响应,通过对胶层破坏和不破坏两种条件下的模拟结果和试验数据进行比对,验证了仿真分析的有效性。邵莲芬等[6]对钢化夹层玻璃和普通夹层玻璃的抗爆性能进行了试验,结果表明钢化夹层玻璃的抗爆性能明显优于普通夹层玻璃。Zhang等[7-8]利用LS-DYNA软件建立爆炸载荷作用聚乙烯醇缩丁醛夹层玻璃动态响应的数值模型,建立了聚乙烯醇缩丁醛夹层玻璃在爆炸载荷作用下的超压- 冲量(p-I)曲线。邓荣兵等[9]利用任意拉格朗日- 欧拉(ALE)有限元法进行了爆炸流场与复杂玻璃幕墙结构相互作用的三维动态仿真(玻璃采用线弹性模型),并与试验结果对比,验证了该仿真方法的可行性。上述研究中选用的玻璃都是夹层钢化玻璃或浮法玻璃,并不是对单层的钢化玻璃进行研究,对单层钢化玻璃p-I曲线[10-11]的研究还未见报道。研究单层钢化玻璃的抗爆性能可以有效地减少因事故爆炸、偶然爆炸、恐怖袭击等事故造成的伤亡和财物损失,对于结构毁伤和防护分析具有参考意义。
冲击波对结构毁伤的p-I准则,是指作用于结构上的超压和冲量同时满足一定条件时,结构就会被破坏,此准则兼顾了超压和冲量两个爆炸参数,其适用范围更广,能够很好地预测冲击波对钢化玻璃的毁伤效应。本文利用数值模拟方法对单层钢化玻璃在爆炸冲击波作用下的抗爆性能进行研究。对试验测得爆炸冲击波载荷进行合理地简化,建立了爆炸冲击波作用于单层钢化玻璃的数值模型,并用场地试验结果和文献[7]中试验结果对模型进行验证。通过计算进而得到爆炸冲击波对钢化玻璃毁伤的p-I曲线和经验公式,与文献[5]、文献[7]、文献[8]中钢化玻璃的破坏规律相吻合。结果表明,本文得到的经验公式可以更好地了解单层钢化玻璃的抗爆性能,为钢化玻璃结构的抗爆设计提供有价值的参考。
1 数值模拟模型
1.1 有限元模型和计算方法
本文研究的玻璃为工业制品中常用的单层钢化玻璃,尺寸为1 300 mm×1 600 mm×10 mm,三维几何模型如图1所示。
模型中单层钢化玻璃采用3D SOLID164 8节点实体单元。用拉格朗日算法来描述玻璃,通过对单层钢化玻璃网格的收敛性及合理性进行研究,综合考虑计算机的计算时间和计算精度,将单层钢化玻璃板厚度方向划分3个网格,长度和宽度方向网格尺寸大小为10 mm. 简化后的爆炸冲击波三角载荷直接加载在钢化玻璃面板单元上。
1.2 爆炸冲击波载荷简化
空气冲击波传播过程中波阵面压力在初始阶段衰减很快,后期衰减平缓,典型的爆炸冲击波超压[12-13]随时间变化的经验公式可描述为
p(t)=pm(1-t/td)e-at/td,
(1)
式中:p(t)为t时刻瞬间超压;pm=ppm-pa为峰值超压,pa为大气压,ppm为最大压力值;a为衰减系数;td为正压作用时间。
本文的主要目的是得到钢化玻璃损伤的p-I曲线,对于结构来说,大部分破坏由爆炸冲击波正压段引起,主要的爆炸参数为正压段的超压和冲量。因此在这里对爆炸冲击波载荷进行简化[14],将试验测得的压力载荷简化为三角形载荷,其中压力峰值按曲线的最大值取值。压力作用时间td=2I/pm,其中I为积分所得冲量,简化后的爆炸冲击波载荷压力- 时间曲线如图2所示。
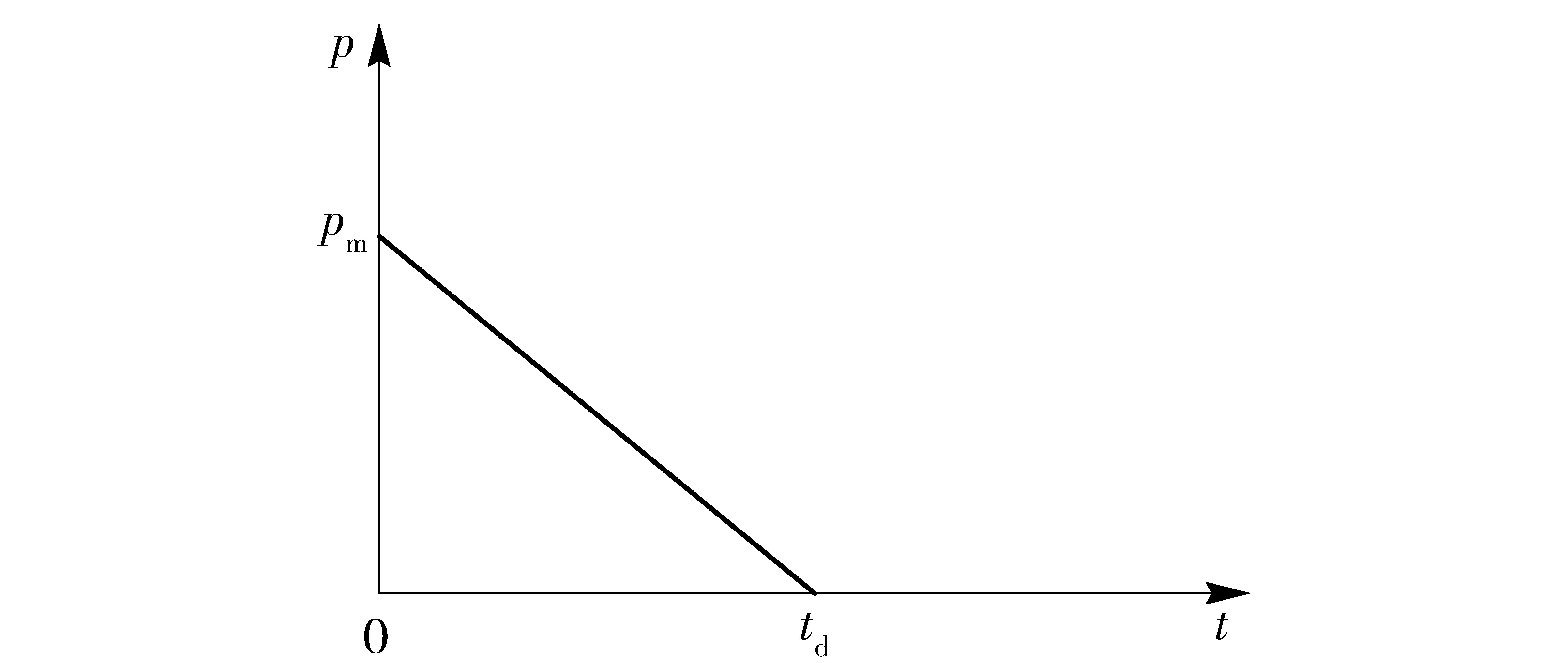
图2 简化三角形载荷Fig.2 Simplified triangular load
1.3 材料模型和边界条件
对钢化玻璃采用线弹性材料模型[15-16],材料参数如表1所示。

表1 钢化玻璃参数
计算中通过增加侵蚀算法[17-18]来实现钢化玻璃材料失效准则的定义,命令为*MAT_ADD_EROSION. 钢化玻璃单元达到破坏条件后,就把失效单元从模型中删除,从而得到单层钢化玻璃裂纹扩展情况。钢化玻璃板四周进行局部固定约束来模拟实际应用中的一种框架支承方式,与场地试验钢化玻璃的框架支撑方式比较接近。通过对极限应变在0.000 5~0.003 0之间多次取值进行数值计算,当单层钢化玻璃的极限应变为0.002 2时,数值计算结果与场地试验结果相符合,可以很好地模拟单层钢化玻璃的破坏。因此,本文中单层钢化玻璃的极限应变为0.002 2是合理的。
2 模型验证
冲击波毁伤效应试验通常可以采用试验室激波管试验和外场化爆试验两种,通过将激波管或化爆产生的冲击波作用于目标效应物,研究其冲击波毁伤效应。本次试验项目组采用第2种方式,即外场化爆试验。试验选取工业制品中常用的单层钢化玻璃尺寸1 300 mm×1 600 mm×10 mm. 固定方式为明框架支承。试验在辽宁省葫芦岛市某试验场地进行,每发试验利用压力传感器测得自由场和钢化玻璃板中心处的冲击波反射超压冲量值,通过高速摄影捕捉钢化玻璃板在不同爆炸冲击波作用下的破坏情况。试验现场布局如图3所示。

图3 场地试验现场布局图Fig.3 Layout of field experiment
对于同一规格的单层钢化玻璃(指厚度、尺寸、加工条件、材料性质等均相同),通过调整爆炸装药与单层钢化玻璃之间的距离进行多次试验,获得不同冲击波毁伤条件下的试验结果。
本文建立的数值模型与试验工况条件相对应,模型中对钢化玻璃板施加4边局部约束的边界条件与场地试验的框架支承比较接近,模拟计算加载到钢化玻璃板的反射超压冲量组合与试验测得反射超压冲量相对应。利用建立的数值模型进行计算,并将计算结果与试验结果进行比对,如表2和表3所示。模拟计算单层钢化玻璃破坏情况如图4所示。
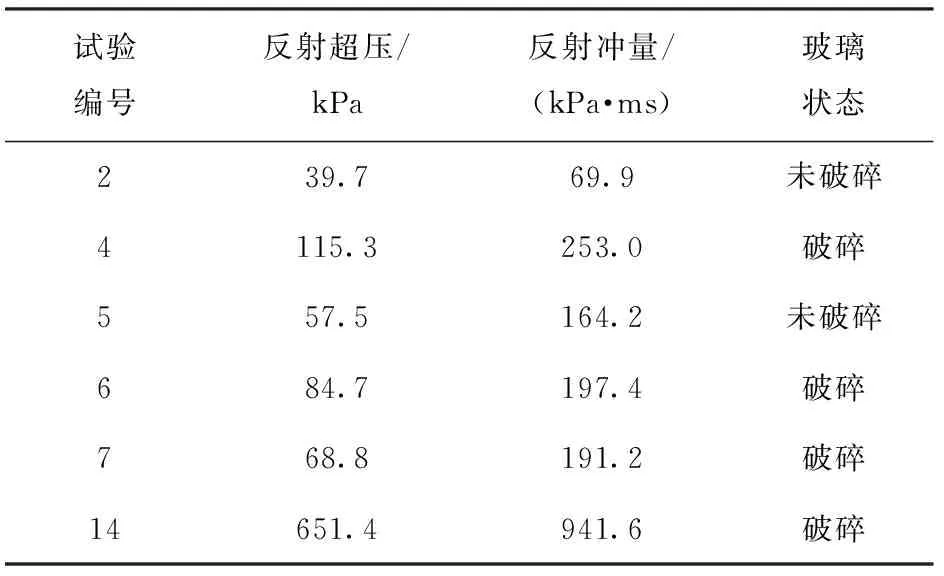
表2 场地试验结果
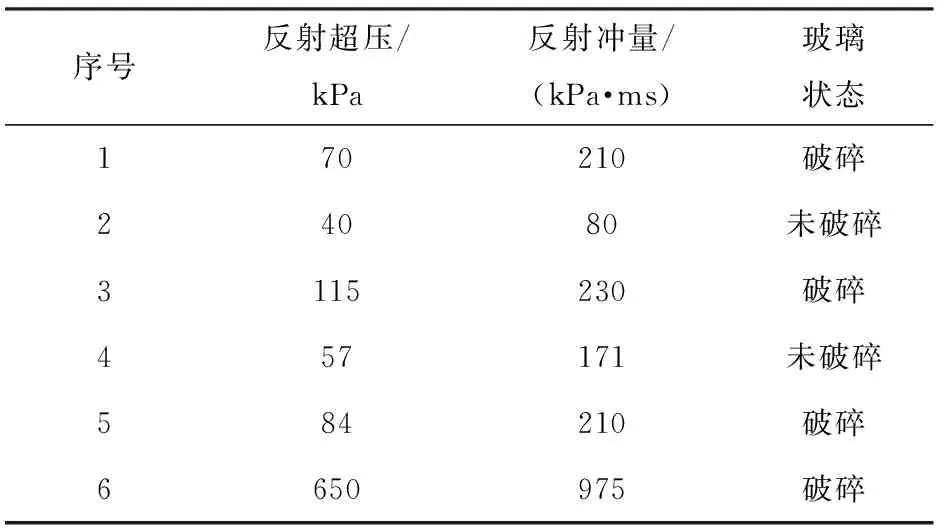
表3 模拟计算结果
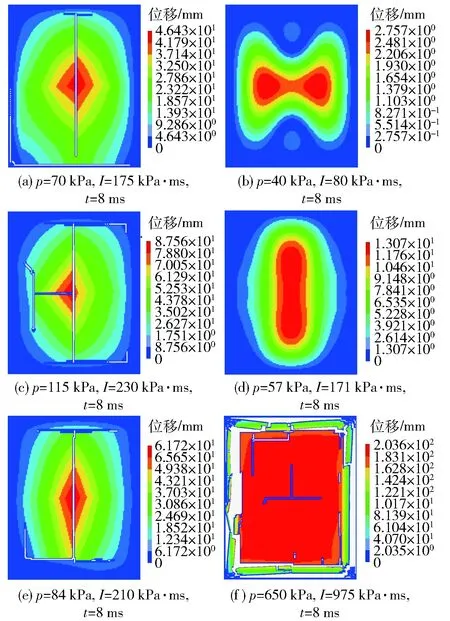
图4 模拟计算钢化玻璃破坏情况及位移云图Fig.4 Simulation damage and displacement contours of tempered glass
从图4模拟结果可以看出,随着施加到钢化玻璃的超压和冲量的增加,钢化玻璃板中裂纹的数目增多、损坏的面积比越来越大,板中心最大位移也越来越大,这一结果与现场拍的照片中,钢化玻璃碎片飞离的距离越远,钢化玻璃破坏越严重相符。
考虑到场地试验周围环境复杂(现场有小土包和土坑),对试验结果会产生影响,因此,表2和表3中试验超压冲量与模拟超压冲量之间存在误差,冲量最大误差为14.2%,超压最大误差为1.74%,误差在可接受范围之内。对于试验结果和模拟结果,钢化玻璃的破坏状态是完全一致的。
为了进一步验证建立数值模型的有效性,利用建立的数值模型计算文献[7]中的试验测得结果相对应的反射超压、冲量组合。文献[7]中钢化玻璃尺寸为1 200 mm×1 500 mm×10 mm,钢化玻璃材料特性与本文一致,固定方式也是框架支承,试验测得反射超压和反射冲量结果如表4所示,模拟计算结果如图5所示。
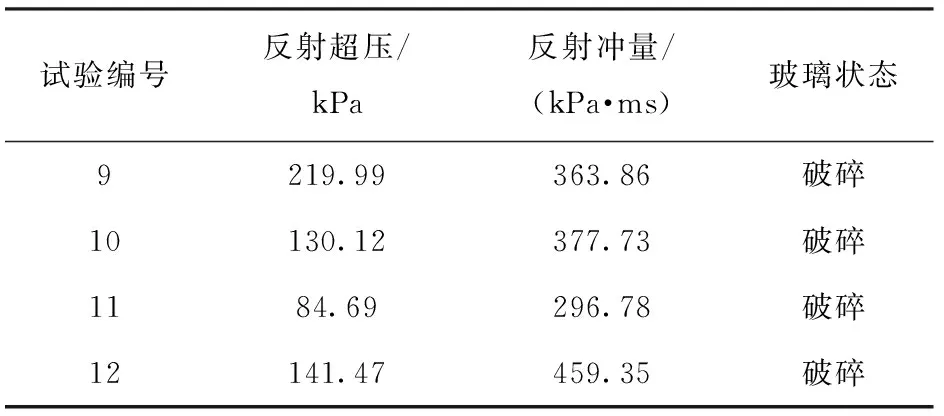
表4 文献[7]中试验结果
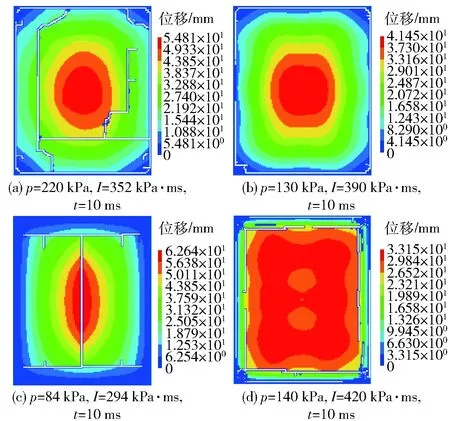
图5 模拟计算文献中钢化玻璃破坏情况及位移云图Fig.5 Simulation damage and displacement contours of tempered glass
由图5可知,模拟计算所得钢化玻璃的破坏情况与文献[7]中的试验结果完全一致,其中计算反射超压与试验测得反射超压最大误差为1.03%,计算反射冲量与试验测得反射冲量最大误差为8.56%,考虑到文献[7]中钢化玻璃板尺寸与本文研究的钢化玻璃板尺寸存在差异,其误差范围是可以接受的。
综上所述,本文建立的数值模型是合理的,能够很好地反映爆炸冲击波对单层钢化玻璃的破坏现象。
3 数值计算结果及p-I曲线建立
3.1 模拟结果
在保证数值模型其他条件参数不变的情况下,只改变冲击波载荷的超压和冲量。在超压一定时,逐渐增加冲量,直到钢化玻璃破坏。钢化玻璃破坏是指模拟结果中钢化玻璃至少有一条裂纹,模拟钢化玻璃破坏与不坏的冲量值在误差5%范围之内,作为一组钢化玻璃破坏的临界超压冲量值。同理,当冲量一定时,逐渐增加超压值,直到钢化玻璃破坏,同样得到一组临界超压冲量值。重复上述过程,通过不断地调整超压冲量值,在LS-DYNA软件平台上进行计算,得到爆炸冲击波对钢化玻璃破坏的超压冲量临界点,如表5所示。从表5中可以看出,当冲量为108 kPa·ms时,超压大于400 kPa,钢化玻璃就会破坏。当超压为27 kPa时,需要很大的冲击波作用时间,即冲量很大时钢化玻璃才会破坏。
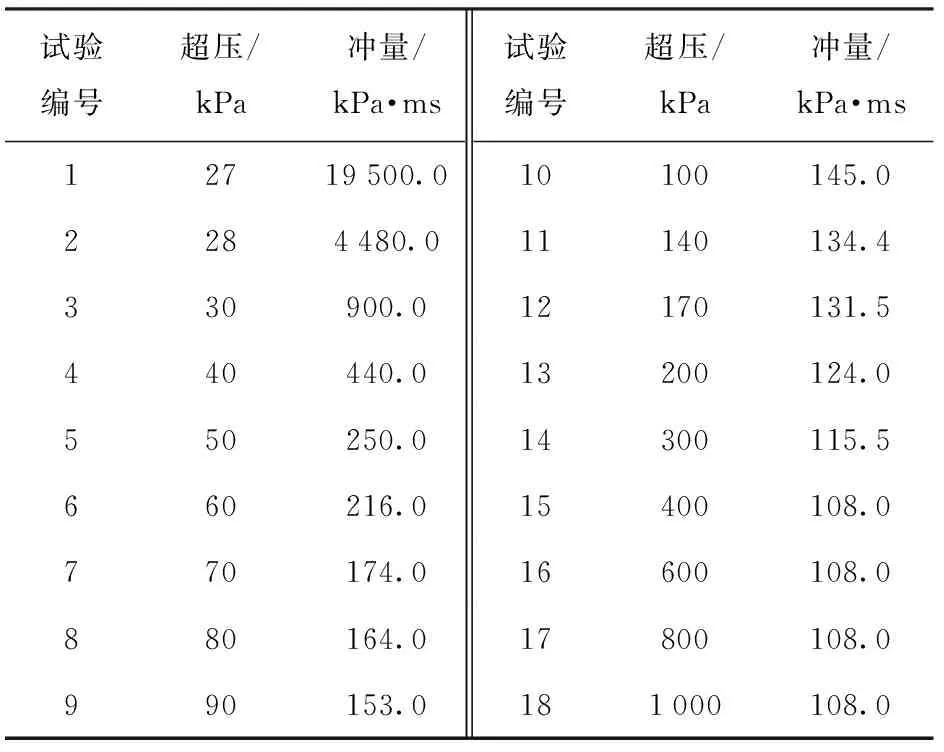
表5 临界反射超压、冲量计算结果
3.2 拟合p-I曲线及经验公式
爆炸冲击波p-I准则是超压和冲量的共同作用满足某一临界条件,目标就被破坏,该准则同时考虑超压和冲量这两个爆炸参数。 对于大多数冲击波作用的目标,该准则是普遍适用的。p-I准则在结构防护设计方面起重要作用,既能够提前预测冲击波对结构的破坏程度,又可以对事故造成的损伤进行定量分析。由表4中的数值计算数据点在Origin软件中作曲线图,可以得到冲击波对钢化玻璃损伤的p-I曲线的数值解,如图6所示。

图6 p-I曲线数值解Fig.6 p-I curve of numerical results
由数值解p-I曲线图可以得到,p-I曲线把整个坐标空间划分为两个区域, 曲线右上方代表钢化玻璃破坏区域,越远离曲线,钢化玻璃损伤越严重;曲线左下方代表钢化玻璃安全区域,越靠近坐标轴位置,钢化玻璃越安全。由图6中可以看出,当超压值小于26 kPa时,无论冲量值多大,钢化玻璃也不会破坏,此时超压对钢化玻璃的破坏起决定作用;当冲量值小于108 kPa·ms时,无论超压值多大,钢化玻璃仍完好,此时冲量对钢化玻璃的破坏起决定作用;当超压大于26 kPa,冲量大于108 kPa·ms时,无论超压还是冲量固定,逐渐增加另一参数,总会与曲线有交点,即钢化玻璃会发生破坏,在此区域内,超压冲量值共同决定钢化玻璃的破坏。综上分析可得单层钢化玻璃损伤的压力渐近线值p0=26 kPa,冲量渐近线值I0=108 kPa·ms.
对于爆炸冲击波对玻璃的损伤效应p-I曲线的预测,一般的经验公式[8]为
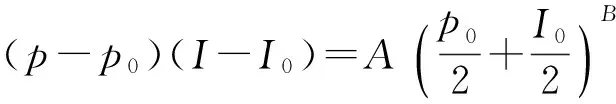
(2)
式中:A、B是常数,与材料和损伤等级有关。
本文通过计算数值点拟合曲线得到A和B的值分别为2.8和1.6. 把经验公式p-I曲线与计算数值解进行比对,如图7所示,由图可以看出数值数据点基本上都在经验公式曲线上及附近,具有很好的相关性,经验公式和数值结果拟合较好,能够反映出钢化玻璃的破坏情况。因此可得,对于单层钢化玻璃板尺寸为1 300 mm×1 600 mm×10 mm,4边采用框架固定支承安装方式,钢化玻璃板损伤的p-I曲线的经验解析式为
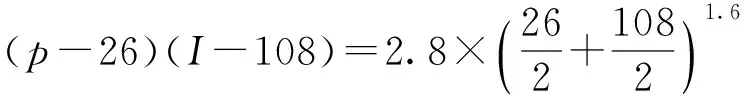
(3)
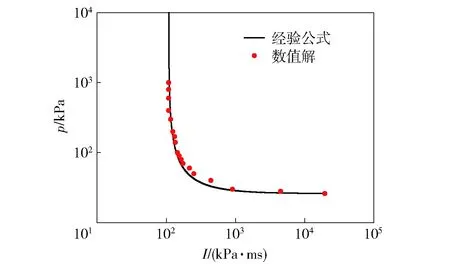
图7 经验公式与计算数值解Fig.7 p-I curves of empirical formula and numerical results
3.3 与文献[5]、文献[7]、 文献[8]中的结果比对
图8为经验公式与文献[5]、文献[7]、 文献[8]中的试验结果和模拟计算结果的比对,由图可以看出文献[7]中10 mm单层钢化玻璃破坏试验结果都在经验公式和数值解p-I曲线的破坏区,文献[5]和文献[8]为6 mm+6 mm夹层钢化玻璃,其破坏点也都在经验公式和数值解p-I曲线破坏区域内。由此可得,利用本文中经验公式所反映的钢化玻璃破坏和文献[5]、文献[7]、 文献[8]中钢化玻璃破坏的规律相吻合,并且文献[5]、文献[7]、 文献[8]中的结果在经验公式曲线中处于损伤更加严重的位置,进一步可得本文中得到的单层钢化玻璃经验公式在钢化玻璃结构抗爆设计中更具合理性。

图8 经验公式与文献[5,7,8]中结果比对Fig.8 Comparison of calculated result of empirical formula and the results in Refs.[5,7,8]
4 结论
本文在ANSYS/LS-DYNA软件平台上建立了钢化玻璃在爆炸冲击波作用下的数值模型,通过数值模拟和试验研究得到以下结论:
1) 通过模拟计算结果得到了尺寸为1 300 mm×1 600 mm×10 mm的单层钢化玻璃、4边采用框架支承方式、在爆炸冲击波作用下的p-I曲线,可以为单层钢化玻璃抗爆设计提供一些参考,并通过曲线拟合得到了经验公式。
2)数值模拟结果和试验结果基本吻合,验证了本文中所建立数值模型的合理。由于单层钢化玻璃的支承方式和厚度对其在冲击波作用下的响应也有较大的影响,对于不同厚度和不同支承方式的单层钢化玻璃p-I曲线和经验公式,需要在今后的工作中继续研究。
References)
[1] 陈海杭, 肖岩. 建筑玻璃幕墙抗爆性能研究综述[J]. 自然灾害学报, 2015, 24(6):150-157. CHEN Hai-hang,XIAO Yan. Literature review of blast resistance of glass curtain wall subjected to blast loading[J].Journal of Natural Disasters,2015,24(6):150-157. (in Chinese)
[2] 宁建国, 王猛. 关于计算爆炸力学的进展与现状[J].力学与实践, 2012,34(1):10-19,69. NING Jian-guo, WANG Meng. Review on computational explosion mechanics[J].Mechanics in Engineering, 2012,34(1):10-19,69. (in Chinese)
[3] 李胜杰. 爆炸载荷下夹层玻璃的动态响应及裂纹扩展的研究[D].太原:太原理工大学, 2015. LI Sheng-jie.Study on the dynamic response and cracks propagation of laminated glass subjected to blast load[D].Taiyuan:Taiyuan University of Technology, 2015. (in Chinese)
[4] Larcher M, Teich M, Gebbeken N, et al.Simulation of laminated glass loaded by air blast waves[J]. Applied Mechanics and Materials,2011,82(8): 69-74.
[5] Larcher M, Solomos G, Casadei F, et al. Experimental and numerical investigations of laminated glass subjected to blast loading[J]. International Journal of Impact Engineering, 2012, 39(1):42-50.
[6] 邵莲芬, 张文忠. 爆炸荷载作用下典型建筑构件破坏特征试验研究[J]. 现代电子技术, 2016,39(15):86-89,94. SHAO Lian-fen,ZHANG Wen-zhong.Experimental study on damage characteristics of typical building component under explosion load[J]. Modern Electronics Technique,2016,39(15):86-89,94. (in Chinese)
[7] Zhang X, Hao H, Wang Z. Experimental investigation of monolithic tempered glass fragment characteristics subjected to blast loads[J].Engineering Structures,2014,75(8):259-275.
[8] Zhang X, Hao H, Ma G. Parametric study of laminated glass window response to blast loads[J].Engineering Structures,2013,56(6): 1707-1717.
[9] 邓荣兵, 金先龙, 陈峻, 等.爆炸冲击波对玻璃幕墙破坏作用的多物质ALE有限元模拟[J]. 高压物理学报, 2010,24(2):81-87. DENG Rong-bing, JIN Xian-long,CHEN Jun, et al. Application of ALE multi-material formulation for blast analysis of glass curtain wall[J]. Chinese Journal of High Pressure Physics, 2010, 24(2):81-87. (in Chinese)
[10] Shi Y, Hao H, Li Z X. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads[J]. International Journal of Impact Engineering. 2008, 35(11):1213-1227.
[11] Idriss J S, Lowak M J. Empirical evaluation of glazing systems in response to blast loads[C]∥2014 Structures Congress.Boston,MA,US:ASCE, 2014: 258-269.
[12] 葛杰, 李国强. 建筑夹层玻璃在冲击荷载下的破坏研究概述[J]. 结构工程师, 2010,26(4):137-143. GE Jie, LI Guo-qiang. A review of research on the failure of architectural laminated glazing under explosive loads[J]. Structural Engineers, 2010, 26(4):137-143. (in Chinese)
[13] 段雷琳, 高轩能. 爆炸冲击荷载下玻璃幕墙建筑抗爆研究[J]. 低温建筑技术,2012, 34(5):41-43. DUAN Lei-lin, GAO Xuan-neng. Study on blast resistant for glassing curtain wall construction under blast loading[J]. Low Temperature Architecture Technology, 2012, 34(5):41-43. (in Chinese)
[14] 张其林, 陶志雄, 王勋, 等. 爆炸作用下夹层玻璃幕墙动力响应试验研究[J]. 建筑结构学报, 2013,34(4):74-80. ZHANG Qi-lin, TAO Zhi-xiong, WANG Xun, et al. Dynamic response research of laminated glass curtain wall subjected to blast loading [J]. Journal of Building Structures, 2013,34(4):74-80. (in Chinese)
[15] Wedding W C.Experimental study of blast resistant glazing system response to explosive loading[D]. Lexington, KY, US: University of Kentucky, 2010:31-145.
[16] Hidallana-Gamage H D, Thambiratnam D P, Perera N J. Influence of interlayer properties on the blast performance of laminated glass panels[J]. Construction and Building Materials, 2015, 98(10): 502-518.
[17] Keyword user’s manual [M].CA, US: Liver-more Software Technology Corporation, 2003.
[18] LS-DYNA theory manual [M].CA, US: Liver more Software Technology Corporation, 2006.
Numerical Investigations on Blast Resistance of Monolithic Tempered Glass Subjected to Shock Wave
LIU Jun1, TIAN Zhou2, ZHONG Wei2,3, XIE Shu-hong1
(1.School of Materials Science and Engineering, Xiangtan University, Xiangtan 411105,Hunan, China; 2. Northwest Institute of Nuclear Technology, Xi’an 710024, Shaanxi, China; 3. School of Mathematical Sciences, Peking University, Beijing 100871, China)
Based on LS-DYNA, the Lagrange method is used to describe the monolithic tempered glass. The linear elastic material model and the erosion algorithm are used to study the monolithic tempered glass. The numerical model is well validated by the field experimental results. The overpressure-impulse curve of blast wave on monolithic tempered glass is obtained through the huge numerical simulation based on the validated model. The empirical formula of damage curve of monolithic tempered glass is also deduced, and the numerical results are compared to the experimental results. The research result shows that the numerical results have good agreement with the experimental results, and the overpressure-impulse curve can provide effective reference for blast resistant design of tempered glass.
explosion mechanics; monolithic tempered glass; numerical simulation; overpressure-impulse curve
2016-10-24
刘俊(1991—),男,硕士研究生。E-mail: 201431101263@smail.xtu.edu.cn
田宙(1967—),男,研究员,博士生导师。E-mail: tianzh2003@163.com
O383+.3
A
1000-1093(2017)07-1402-07
10.3969/j.issn.1000-1093.2017.07.019

