ATM交易状态特征分析与异常检测的研究与实现
隋晓雪+彭韦一+刘鱼迁
【摘 要】本文运用数据挖掘、几何知识、统计学等知识对ATM应用系统交易状态的业务量、交易成功率、交易响应时间三个指标进行数据分析,提取了ATM交易状态的特征参数。借助MATLAB、R语言、SPSS与Excel等办公软件,对ATM交易状态特征进行分析。运用K-Means聚类分析、Pearson相关性分析、建立logistic回归模型、决策树预警模型,进一步分析了交易数据分布存在的特征,建立相应预警模型,对该交易系统应用可用性异常情况做出及时有效的预警。为ATM应用系统的规范化管理提供了参考。
【关键词】K-Means聚类分析;Pearson相关性分析;logistic回归分析;决策树
一、问题的提出与分析
随着银行卡业务的快速发展,自助设备在银行对外服务中的作用日渐突出。作为自助现金服务的主要渠道,ATM机能够为客户提供24小时不间断便捷服务,其承担的业务是银行服务的有效延伸。因此,如何提高ATM应用系统运行效率便成为本课题分析研究的主要工作。本题旨在通过对下设分行的交易信息进行汇总统计、数据分析,来捕捉ATM应用系统的运行情况以及时发现异常或故障,并及时发出警报,以保证系统正常高效的运行。
针对问题一(选择、提取和分析 ATM 交易状态的特征参数):
由于所给各分行交易信息情况以分钟计,数据量过于庞大,软件运行困难,为简化问题,暂时先考虑每小时银行ATM交易状态特征分析与异常检测。
为防止异常值在数据分析和解算结果中造成显著的变化,提高数据的精确性,首先提取异常值。用R语言实现K—means算法做聚类分析,将离群异常值剔除,并将异常交易数据标记为1,非异常数据标记为0,进一步寻找参数与ATM交易状态的特征参数;然后,利用SPSS软件做Pearson相关分析,得到相关系图表;然后通过查阅相关资料,选择尽可能相关的特征参数,用logistic回归模型提取特征参数,分析ATM交易状态。
针对问题二(设计一套交易状态异常检测方案,对该交易系统的应用可用性异常情况及时预警):
为能确保ATM交易系统正常运行,对其可能出现的异常交易进行及时监控、检测并报警,我们需建立一种预测模型。
首先,我们用Excel画出交易数据时间序列图,分析数据规律,找出工作日与非工作日。再用SPSS对所有交易进行聚类,画出系统聚类图——分类树状图,即将交易数据分为不同的类别,即分为节假日高峰期、节假日低谷期、工作日高峰期、工作日低谷期进行分析。将1-3月份交易数据作为训练数据,用4月份交易数据作为预测数据集,使用训练数据建立决策树模型,使用决策树分别对预测数据集进行异常值检测,即将每个类别的每种方法的真实异常值和预测异常值进行对比,得到每种模型的错误率。最终设计出最佳ATM异常检测方案。
二、模型的建立与求解
(一)检测异常交易数据
查阅相关资料,本文尝试利用基于距离的方法将孤立或者没有足够多邻居的数据作为异常。利用MATLAB实现K—means算法初步显示异常数据值,进一步利用R语言对各数据值做聚类分析以提取异常点,该算法以划分为基本出发点,对给定的数据集,利用分裂法构造k个分组,每一个分组就代表一个聚类,通过反复迭代的方法改变分组,使得同一分组中的数据记录越来越近,不同分组中的数据越来越远,从而达到提取异常值的目的。
(二)ATM交易状态特征参数的确定
本文先对已知的三个指标(即交易量、交易成功率、交易响应时间)和异常交易进行相关性分析,并且尽可能去寻找能够更好描述交易状态的特征参数,对这些参数用logistic回归模型进行提取和分析,最终确定衡量ATM交易状态的特征参数。
(三)预警模型的建立
利用系统聚类法开始将n个样品各自作为一类,并规定样品之间的距离和类与类之间的距离,然后将距离最近的两类合并成一个新类,计算新类与其他类的距离;重复进行两个最近类的合并,每次减少一类,直至所有的样品合并为一类。本文利用SPSS将数据分为工作日进和非工作日(接下来都以非工作日为例,其他情况类似进行分析),通过系统聚类法找到业务低谷时间和正常业务时间段。
进一步利用决策树建立预测模型,将1-3月份交易数据作为训练数据,利用SPSS对1—3月份数据建立决策树模型,从根节点开始进行不断地划分,进行剪枝,不断改变划分节点的纯度,以确定最佳划分的标准。最后用4月份交易数据作为预测数据集,将4月份交易数据应用先前建立的决策模型,进行异常值预测,最终确立决策树模型。
三、模型求解与结果分析
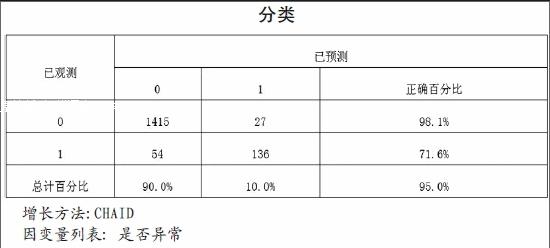
SPSS运行下的决策树预测模在导入四月份的交易数据后,对其异常交易进行预测,得到如下预测结果:
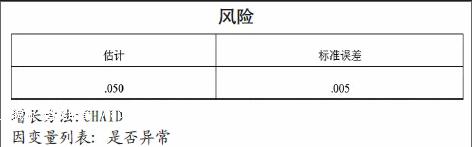
在以上解决过程中,我们将1—3月份交易数据作为训练数据建立决策树模型,而4月份交易数据作为预测数据,对异常交易值进行预测,进一步验证模型的准确性,实用性,发现其无论是在工作日或非工作日,低谷时间段或是正常时间段,预测值与已观测数据值达到高度的一致性,其正确百分比达到95%.而预测标准误差仅0.005,如下表:
参考文献:
[1]李春林,陈旭红,应用多元统计分析,北京:清华大学出版社,2013年
[2]许汝福,Logistic回归变量筛选及回归方法选择实例分析[J],中國循证医学杂志,2016(11):1360—1364
[3]V.N.Vapnik,The natural of statistical learning theory,Springer,New York,1995
[4]王艳兵,赵锐,姚青,基于可变精度的ID3改进算法[J],计算机工程与设计,27(14):2683—2685,2006年
[5]刘凤芹,K—means聚类算法改进研究,山东师范大学硕士学位论文,2013年

