利用含二面角误差的角锥棱镜阵列实现反射光束均匀发散的方法

周晓凤 戚祖敏 罗向前 刘长安 朱建辉 王泽华 张轶訾 彦勇

(西北核技术研究所,西安710024)

利用含二面角误差的角锥棱镜阵列实现反射光束均匀发散的方法

周晓凤 戚祖敏†罗向前 刘长安 朱建辉 王泽华 张轶訾 彦勇

(西北核技术研究所,西安710024)

(2016年10月16日收到;2016年12月11日收到修改稿)

角锥棱镜常应用于光电跟踪、卫星通信、干涉仪等领域.在一些特殊应用场合中,要求经角锥棱镜反射的光束具有一定的发散角,以实现对距离激光器较远位置处探测器的覆盖.由于标准角锥棱镜不具备对光束发散的功能,本文利用含二面角误差的角锥棱镜对反射光束的不均匀发散特性,提出利用角锥棱镜阵列实现对反射光束均匀发散的方法和设计原则.采用衍射光学理论分析了所提方法及其设计原则的可行性,并依此设计了一个发散半角为0.5Mrad的角锥棱镜阵列.分析了光束参数、结构参数对反射光束远场衍射特性的影响,结果表明,入射光斑强度分布对反射光束发散半角没有影响,当角锥阵列满足点光源条件时,传输距离对反射光斑的角向均匀性没有影响;当阵元数超过一定值时,均匀性不再显著变化,但反射光斑的强度将进一步增加.在工程应用中,角锥棱镜阵列安装方位角误差对反射特性影响不显著,但角锥棱镜二面角的加工精度对反射特性影响较大,可通过进一步增加阵元数加以解决.

角锥棱镜,阵列,发散半角,光电跟踪

1 引言

角锥棱镜作为一种高精度的光学元件,其基本功能是实现对入射光束的原方向返回[1].由于角锥棱镜的优良特性,其被广泛应用于光电跟踪[2]、卫星通信[3]、干涉仪[4−6]等领域.当激光器发射的光束传输到角锥棱镜时,将被原方向返回至与激光器处于同一位置的探测器,从而实现光电跟踪及通信.

在一些特殊的应用场合中,角锥棱镜固定在空中运动平台上,激光器和探测器位于地面不同位置处,两者间的距离为d,且d≫2.44λL/D,其中λ为反射光束的波长,L为角锥棱镜与探测器的距离,D为角锥棱镜的通光口径,即d远大于反射光束的衍射极限.此时,地面激光器发射的光束不能经过空中标准角锥棱镜反射至探测器处.必须对反射光束进行发散,实现反射光斑对探测器的覆盖.由于角锥棱镜的优良特性,任意方向入射的光束都能被原方向返回,在存在俯仰、航向、滚转等姿态角误差的空中平台中,很难找到更好的光学元件替代品.

研究表明,当角锥棱镜存在二面角误差时,反射光束分化为六个子光束,每个子光斑的能量分布几乎相同,且其能量中心近似分布在同一个圆周上,表现为发散的特性[7,8].利用角锥棱镜的这一特性,即可实现对反射光束的发散.然而,随着二面角误差和传输距离的增加,反射光斑的角向均匀性将进一步降低,导致探测器接收反射光强度忽强忽弱,不利于实现对空中运动目标的闭环锁定跟踪.在星载平台上,常采用球形角锥棱镜阵列解决大范围入射角度下的反射问题[9],本文借鉴角锥棱镜阵列的思路,提出利用含二面角误差的角锥棱镜阵列实现反射光束发散的方法,以在远场形成角向均匀的环形光斑,实现对空中运动平台的稳定跟踪.

2 含二面角误差角锥棱镜的后向衍射特性

2.1 理论分析

图1为入射面为三角形的角锥棱镜结构示意图,在标准角锥棱镜中,面AOB,AOC和BOC之间的夹角满足α=β=γ=π/2.当角锥棱镜存在二面角误差时,三个二面角可表示为

其中δ12,δ23和δ31分别为三个面的二面角误差.

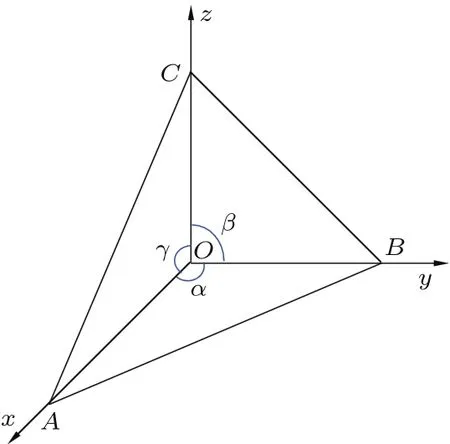
图1 角锥棱镜结构示意图Fig.1.ScheMatic structure of the cube-corner retrorefl ector(CCR).

由于反射光束传输距离远大于角锥棱镜的通光口径,反射光束必然受到衍射效应的影响.当观察屏远离角锥棱镜及邻近光轴时,远场光斑符合菲涅耳衍射条件

其中z为远场观测屏与角锥棱镜的距离;λ为入射或反射光束波长;x,y,z为观测屏坐标;x′,y′,z′为角锥棱镜坐标.远场z处的衍射光斑为[10]

其中E(x,y,z)为远场光斑复振幅分布,Eout(x′,y′)为角锥棱镜出射面的复振幅分布;k为入射或反射光束波数;fx和fy分别为沿x方向和y方向的空间频率.

则入射光束经过角锥棱镜反射后,其出射光场的复振幅分布为

其中Ein(x′,y′)为入射光场复振幅分布,由于角锥棱镜与激光器的距离足够远,入射至角锥棱镜的光束可认为是平面波;A(x′,y′)为角锥棱镜的有效衍射区域;ϕc为角锥棱镜二面角误差引起的相位分布.

为了便于机械工装,采用圆切割的角锥棱镜.当角锥棱镜的通光口径D为30mm、二面角误差皆为20′′、三条棱的倒棱宽度l为0.5 mm时,利用矢量形式的光线折射和反射定律,对含二面角误差角锥棱镜的A(x′,y′)和ϕc进行数值求解[11],图2所示为角锥棱镜安装方位角φ=0◦时的有效衍射区域和相位分布.倒棱工艺将角锥棱镜的有效衍射区域分割为六个扇形区域.数值计算表明,当二面角误差为正值时,相位分布ϕc随角锥棱镜入射面半径的增加而增加,随二面角误差的增加而准线性增加,由相位分布可以预测反射光束为发散光束,且发散半角随二面角误差的增加而线性增加.

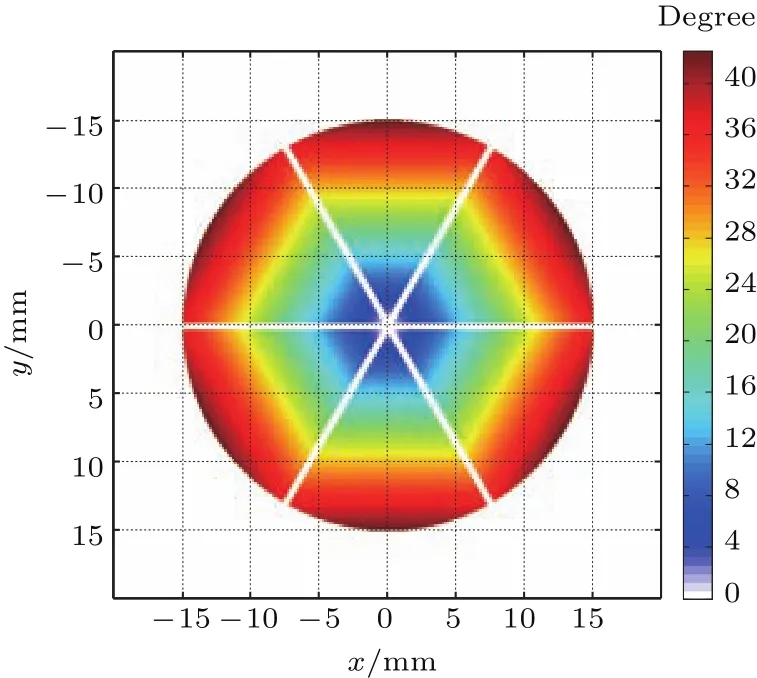
图2 (网刊彩色)角锥棱镜的有效衍射区域和相位分布(φ=0◦)Fig.2.(color on line)D iff raction aperture and phase distribution of the CCR(φ=0◦).

由角锥棱镜的有效衍射区域和相位分布,理论上利用(3)式和(4)式可计算得到反射光束的远场分布.由于反射光束随着传播距离z的增加而逐渐发散,在计算过程中,取样定理要求取样点的频率必须大于被取样信号最高频率的2倍,离散数据点的最大频率应大于被取样信号最大频率的2倍,计算量随着z的增加迅速增加,导致计算时长无法接受.Coy[12]以及Rydberg和Bengtsson[13]提出采用两步法解决菲涅尔衍射计算量超大的问题,两步法使观测屏和光源屏网格数量相等,引入系数m定义观测屏和光源屏网格大小之比,显著降低计算量.本文采用两步法求解含二面角误差角锥棱镜的发散传输问题.

当入射光束的功率密度为1 W/m2、波长为1064 nm,角锥棱镜的通光口径D为30 mm、二面角误差皆为20′′、三条棱的倒角宽度l为0.5mm时,利用两步法求解得到反射光束传输10 km后的光斑如图3所示.反射光束分化为六个子光束,六个子光束能量中心所处圆周的直径D0约为10 m,在此定义角反射器的发散半角为

根据定义,可计算得到此时角反射器的发散半角约为0.5Mrad.图4给出了反射光斑功率密度沿y轴的分布,可知每个子光束的最大功率密度约为0.1mW/m2、将功率密度降为最大值一半时的宽度定义为每个子光束的光斑直径ds,定义每个子光斑的发散半角θs为

图3 (网刊彩色)单个含二面角误差角锥棱镜的远场衍射光斑(φ=0◦)Fig.3.(color on line)Diff raction pattern of single CCR w ith d ihed ral angle tolerances at far-field(φ=0◦).

由图4可得ds约为0.8m,根据定义,每个子光斑的发散半角θs约为0.04 Mrad.由图3和图4可知,平行光束经过含二面角误差的角锥棱镜反射后,反射光束被发散六个子光束,但反射光斑的角向均匀性较差.

图4 单个含二面角误差角锥棱镜的远场光斑功率密度沿y轴的分布(φ=0◦)Fig.4.Power density distribution of the diff raction pattern along x-axis generated by single CCR w ith dihed ral angle tolerances at far-field(φ=0◦).

2.2 发散特性与角锥棱镜参数的依赖关系

图5 (网刊彩色)单个角锥棱镜不同方位角下的远场衍射光斑(a)φ=15◦;(b)φ=30◦Fig.5.(color on line)D iff raction pattern of single CCR w ith d iff erent fixed aziMu th at far-field:(a)φ=15◦;(b)φ=30◦.

改变角锥棱镜的安装方位角φ,得到不同方位角下的远场光斑,如图5所示.结果表明,当角锥棱镜的方位角变化时,远场光斑随之旋转,旋转角度与方位角变化角度相等.利用角锥棱镜这一特性,建立角锥棱镜阵列模型,合理安排不同阵元之间的方位角,可在远场形成角向均匀的环形光斑.

当三个二面角误差不相等时,六个子光斑的能量中心不能分布在同一个圆周上,本文不进行讨论.当δ12=δ23=δ31=δ时,改变δ,得到不同二面角误差下的发散半角θ,如图6所示,反射光束的发散半角θ随二面角误差δ的增加而准线性增加,与相位分析预测结果一致.对θ关于δ的依赖关系进行线性拟合,拟合结果为

依据(7)式,得到的拟合曲线如图6所示,拟合结果与数值计算结果的均方差为7.331×10−5,可见(6)式能较好地描述反射光束发散半角与二面角误差的依赖关系,将在设计角锥棱镜阵列时使用.

图6 不同二面角误差下的发散半角Fig.6.D ivergence half-angle w ith d iff erent d ihed ral angle tolerances.

3 角锥棱镜阵列设计原则

由单个含二面角误差角锥棱镜的光学特性,利用相同结构参数的角锥棱镜,通过组阵方式进行强弱互补,实现反射光束的均匀发散.一个阵列主要由三个要素组成：阵元、阵元数及阵元分布形式.角锥棱镜阵列的目标是在远场形成发散半角为θ(θ≫2.44λ/D)且角向均匀的环形光斑.

为了实现对反射光束的发散,需采用含二面角误差的角锥棱镜作为阵元,单个阵元的发散半角为θ,依据(7)式,得到单个角锥棱镜的二面角误差δ,并对单个含二面角误差的角锥棱镜进行计算,得到该二面角误差下子光斑的发散半角θs.阵元数量和分布形式的选择取决于形成角向均匀反射光斑的技术指标要求.当角锥棱镜距离探测器足够远时,角锥棱镜在远场相当于一个点光源,在理论上,阵元的几何位置分布对远场光斑分布没有影响.因此,采用平面组阵形式,阵元之间的分布在满足机械工装前提下,尽可能降低角锥棱镜阵列所占的面积.由2.2节可知,反射光斑的分布依赖于角锥棱镜的安装方位角,因此,在确定单个角锥棱镜的二面角误差后,重点需确定阵元的数量ns及安装方位角φn.在理想情况下,角锥棱镜阵列每个阵元的六个反射子光斑能两两相连,且均布在发散半角为θ的圆周上,即能形成角向较为均匀的环形光斑.由几何关系可得阵元数ns和安装方位角φn满足

图7 角锥棱镜阵列布局图Fig.7.Layout of the CCR array.

其中round(x)代表四舍五入函数;n为角锥棱镜阵元的编号,n=1,2,···,ns.

依据设计原则,当反射光束发散半角θ的设计值为0.5 Mrad时,由(7)式得到单个角锥棱镜的二面角误差约为20′′,由(8)式得到角锥棱镜阵列阵元数ns为6,由(9)式得到相邻阵元间的安装方位角间隔∆φn约为0.174 rad,通过角锥棱镜支撑结构的机械设计和加工精度可以保证.为尽可能减小角锥棱镜的面积,建立如图7所示的角锥棱镜阵列,共有六个结构参数相同的角锥棱镜,一个角锥棱镜位于中央位置,其余五个均布在周围,距离中央角锥的最短距离d0为10mm,按照(9)式设置每个角锥棱镜的安装方位角,如图7所示,图中已考虑倒棱工艺对角锥棱镜有效衍射区域带来的影响.

对角锥棱镜阵列的远场衍射光斑进行数值计算,得到距离角锥棱镜阵列10 km远处的反射光斑,如图8所示.反射光斑为一个角向较为均匀的圆环,径向宽度约为0.8 m,发散半角约为0.5 Mrad.由于不同阵元之间的反射光斑相互干涉的原因,反射光斑呈现类条纹分布.在实际使用情况中,由于大气湍流等因素,反射光束的相干长度将降低,反射光斑的干涉条纹将弱化.当角锥棱镜与探测器的距离一定时,无论角锥棱镜的姿态随空中运动平台如何改变,都能确保探测器位于环带内.

图8 (网刊彩色)角锥棱镜阵列远场衍射光斑Fig.8.(color on line)Diff raction pattern of CCR array at far-field.

4 角锥棱镜阵列反射特性的影响因素分析

由于角锥棱镜阵列的发散半角取决于单个角锥棱镜的二面角误差,角锥棱镜阵列的发散半角与二面角误差满足(7)式.因此,采用单一变量法,主要研究入射光斑强度、入射光束角度、反射光束传输距离等光束参数,及阵元数、安装方位角误差、角锥棱镜加工精度等结构参数对反射特性的影响.

4.1 光束参数对反射特性的影响

图9 (网刊彩色)高斯光束入射角锥棱镜的光斑分布(a)角锥棱镜轴向位置处的光强分布;(b)角锥棱镜中心位于(a)中(0,0)处的反射光斑;(c)角锥棱镜中心位于(a)中(0,20 cm)处的反射光斑Fig.9.(color on line)Intensity d istribu tion of thegaussian beaMincident to CCR array:(a)Intensity distribution of the gaussian beaMat the axial position of the CCR array;(b)refl ection pattern when the center of the CCR array is located at coord inate(0,0)in(a);(c)refl ection pattern when the center of the CCR array is located at coord inate(0,20 cm)in(a).

在实际使用中,入射到角锥棱镜阵列的光波并非严格的平面波,尤其是角锥棱镜距离激光器较近或激光器出瞳口径(或束腰半径)较大时,需要考虑入射光斑的复振幅分布.以基模高斯光束入射为例,研究非均匀光波入射角锥棱镜阵列的反射光斑分布.保持角锥棱镜阵列和激光器的距离不变,高斯光束光轴与角锥棱镜阵列中心轴重合,高斯光束光腰半径ω0设为0.5 m,使入射至角锥棱镜阵列的光束为非平面波.图9(a)给出了角锥棱镜阵列轴向位置处的光强分布,最大功率密度为1W/m2.当角锥棱镜中心阵元的中心位于图9(a)中的(0,0)坐标处时,将入射光场的复振幅分布代入(4)式,得到基模高斯光束正入射角锥棱镜阵列的反射光斑,如图9(b)所示,反射光斑的发散半角和功率密度分布几乎不变.当角锥棱镜中心阵元的中心位于图9(a)中的(0,20 cm)坐标处时,角锥棱镜阵列不处于高斯光束的中心,得到的反射光斑如图9(c)所示,反射光束的发散半角保持不变,但强度显著降低.反射光斑在角向上存在不均匀现象,但不显著.这是由于入射光强在角锥棱镜每个阵元区域内变化不大,且分离成六个子光束分布在反射光斑的角向相同间隔的位置.若在实际中非基模高斯光束入射,只需将入射光场代入(4)式即可得到远场衍射光斑.

保持平面波入射,研究光束不同入射角θi和方位角φi下的反射光斑,如图10所示,斜入射条件下,反射光束的发散半角保持不变,且皆为环形光斑;但环形光斑角向不再均匀,在圆周上存在加强和减弱区域,改变光束的方位角,加强区域的相对位置发生旋转,这是由单个含角误差角锥棱镜斜入射特性决定[8,14]的.

保持平面波正入射条件不变,改变反射光束的传输距离,如图11所示.当传输距离较近时,角锥棱镜阵列不满足点光源条件,反射光斑为不规则环形,与角锥棱镜阵列阵元间的分布位置有关,如图11(a)所示.若在实际使用中,角锥棱镜阵列与探测器的距离较近,可适当减小单个角锥棱镜的通光口径,使阵列满足点光源条件.当进一步将传输距离增加至1000 km,反射光斑图样与10 km时没有显著变化,如图11(b)和图8所示,只是反射光斑的半径和功率密度发生了相应的变化.因此,当角锥棱镜阵列满足点光源条件时,角锥阵列的反射光斑角向均匀性并不会随传输距离的变化而变化,如图11(b)所示.

图10 (网刊彩色)不同光束入射角和方位角下的远场衍射光斑(a)θi=30◦,φi=0◦;(b)θi=30◦,φi=90◦Fig.10.(color on line)Diff raction pattern of CCR array w ith diff erent incident angle and azimuth angle at far-field:(a)θi=30◦,φi=0◦;(b)θi=30◦,φi=90◦.

图11 (网刊彩色)角锥棱镜阵列不同传输距离处的远场衍射光斑(a)L=2 km;(b)L=1000 kmFig.11.(color on line)D iff raction pattern of CCR array w ith diff erent p ropagation distance at far-field:(a)L=2 km;(b)L=1000 km.

4.2 结构参数对反射特性的影响

保持角锥棱镜阵列的中心阵元位置及平面波正入射条件不变,改变周围角锥棱镜的数量ns,同时按照(9)式设置各角锥棱镜的安装方位角φn.图12给出了不同阵元数ns下的远场衍射光斑,反射光束的传输距离L=10 km.随着阵元数的增加,反射光斑的均匀性及功率密度逐渐增加.在当前技术参数下,阵元数ns为3或4难于满足均匀性的要求;当阵元数ns>5时,均匀性满足要求,随着阵元数的进一步增加,反射光斑的最大功率密度将增加.由于在理论计算角锥棱镜阵元数时,采用半高宽作为子光束的几何尺寸,在角锥棱镜阵列中,相邻子光束间尺寸大于半高宽区域的光由于干涉得到增强,因此,实际满足均匀性要求的阵元数略小于(8)式计算得到的结果.

图12 (网刊彩色)角锥棱镜阵列不同阵元数下的远场衍射光斑(a)n s=3;(b)n s=4;(c)n s=5;(b)n s=7Fig.12.(color on line)D iff raction pattern of CCR array w ith d iff erent n s at far-field:(a)n s=3;(b)n s=4;(c)n s=5;(b)n s=7.

在工程运用中,角锥棱镜阵列中单个角锥棱镜的安装和加工误差可能会影响远场反射光斑,采用机械结构设计可以将单个角锥棱镜的实际安装方位角误差控制±1◦方位内,为放大安装误差对反射光斑的影响,将角锥棱镜的安装方位角设为

由(10)式可知,相邻角锥棱镜的安装方位角误差达到2◦.图13给出了含安装方位角误差时的反射光斑,在该安装方位角误差下,远场反射光斑的发散半角保持不变.由于安装方位角误差的影响,相邻角锥棱镜的六个子光斑的相干叠加区域增加或减少,从而导致部分区域相干增强、部分区域相干减弱,相比于图8,最大功率密度增加约40µW/m2,增幅约10%,但由于增强或减弱区域较小,不影响角锥阵列的应用.

由于加工工艺的限制,单个角锥棱镜的加工精度不可能精确到90◦20′′,目前角锥棱镜的加工精度可以达到2′′.为放大加工精度对反射光斑的影响,以δ12=25′′,δ23=20′′,δ31=15′′为例,简单研究加工精度对角锥棱镜阵列反射特性的影响,图14(a)为单个角锥棱镜的远场反射光斑,六个子光束不再沿角向均匀分布,导致按(9)式分布的角锥棱镜的远场反射光斑不再角向均匀,如图14(b)所示.在三个二面角误差相差较大,即六个子光斑在距离中心的距离相差较大的情况下,单个角锥棱镜在特定发射半角下的子光斑只有两个,可采用的方法是进一步增加阵元数,且角锥棱镜的安装方位角设为

图14(c)为按照(11)式进行组阵时的反射光斑,其中ns=10,D=30 mm,d0=20 mm,反射光斑的角向均匀性显著改善.由于角锥棱镜二面角误差的不一致性,六个子光束将处于不同的半径的圆周上,从而导致反射光斑在径向上的宽度进一步增加.在工程实际中,单个角锥棱镜的二面角误差可通过光学方法进行测量,将所有阵元的二面角误差代入数值计算程序,进行装配前的进一步优化,从而最终确定各阵元的安装方位角.

图13 (网刊彩色)考虑安装方位角误差时的角锥棱镜阵列反射光斑布Fig.13.(color online)Refl ection pattern of the CCR array w ith consideration of the asseMb lage aziMuth error.

图14 (网刊彩色)角锥棱镜三个二面角误差不一致时角锥阵列的远场反射光斑(a)当δ12=25′′,δ23=20′′,δ31=15′′时,单个角锥棱镜的反射光斑;(b)当δ12=25′′,δ23=20′′,δ31=15′′,n s=6时角锥阵列的反射光斑;(c)当δ12=25′′,δ23=20′′,δ31=15′′,n s=10时角锥阵列的反射光斑Fig.14.(color on line)Refl ection pattern of CCR array w ith d iff erent d ihed ralangle tolerances:(a)Refl ection pattern of single CCR w henδ12=25′′,δ23=20′′,δ31=15′′;(b)refl ection pattern of CCR array w hen δ12=25′′,δ23=20′′,δ31=15′′,n s=6;(c)refl ection pattern of CCR array w henδ12=25′′,δ23=20′′,δ31=15′′,n s=10.

5 结论

含二面角误差的角锥棱镜能实现对反射光束的发散,其发散半角随二面角误差的增加而准线性增加,但反射光斑的强度存在角向不均匀性,在远场形成六个子光斑,且六个子光斑在角向的相对位置与角锥棱镜的安装方位角相关.利用含二面角误差角锥棱镜的特性,采用合适数量结构参数相同的角锥棱镜进行组阵,合理设置不同角锥棱镜的安装方位角,即可实现对反射光束的均匀发散.利用衍射光学理论,分析了含二面角误差的角锥棱镜及其阵列的远场衍射特性.提出了具有均匀发散特性角锥棱镜阵列的设计原则,并依此设计了发散半角为0.5 Mrad的角锥棱镜阵列.研究了光束参数、结构参数对反射光束远场衍射特性的影响,结果表明,入射光斑强度分布对反射光束发散半角没有影响,当角锥阵列满足点光源条件时,传输距离对反射光斑的角向均匀性没有影响;当阵元数逐渐增加时,反射光束的角向分布更加均匀;当阵元数超过一定值时,均匀性不再显著变化,但反射光斑的强度将进一步增加.在工程中,安装方位角误差对反射特性影响不显著,但角锥棱镜二面角的加工精度对反射特性影响较大,可通过进一步增加阵元数加以解决.

[1]Zurasky J L 1976 Appl.Opt.15 445

[2]Liu J Y,Yang J Q,Dong D F,Zhou W H 2015 Opt.Precision Eng.23 1558(in Chinese)[刘娇月,杨聚庆,董登峰,周维虎2015光学精密工程23 1558]

[3]W ang L G,W u Z S,W ang MJ 2013 Acta Phys.Sin.62 164210(in Chinese)[王利国,吴振森,王明军2013物理学报62 164210]

[4]W ang J C,Zhang C M,Zhao B C,Liu N 2010 Acta Phys.Sin.59 1625(in Chinese)[王金婵,张淳民,赵葆常,刘宁2010物理学报59 1625]

[5]Zhang X N,Zhang C M2012 Acta Phys.Sin.61 104210(in Chinese)[张宣妮,张淳民2012物理学报61 104210]

[6]Tang Y H,Zhang C M,Liu H C,Chen G D,He J 2005 Acta Phys.Sin.54 4065(in Chinese)[唐远河,张淳民,刘汉臣,陈光德,贺健2005物理学报54 4065]

[7]N ie H,W eng X T,Li S,Liu J Y 2003 Acta Opt.Sin.23 1470(in Chinese)[聂辉,翁兴涛,李松,刘基余2003光学学报23 1470]

[8]Zhou H,Li S,Zheng G X,Gao J L 2009 Acta Opt.Sin.29 60(in Chinese)[周辉,李松,郑国兴,高俊玲2009光学学报29 60]

[9]W ang T,W ang W,Geng D,Du P,Gong M2014 Opt.Spectrosc.117 158

[10]Ji J R 2007 Advanced Optical Course(Beijing:Science Press)pp295–299(in Chinese)[季家镕2007高等光学教程(北京:科学出版社)第295—299页]

[11]Zhou,H,Li S,Zheng G X 2011 Opt.Rev.18 1

[12]Coy S 2005 Proc.SPIE 589405

[13]Rydberg C,Bengtsson J 2006 J.Opt.Soc.Am.A 23 1616

[14]Liu W L,Ouyang J F,Qu X H 2009 Opt.Precision Eng.17 286(in Chinese)[刘万里,欧阳健飞,曲兴华2009光学精密工程17 286]

(Received 16 October 2016;revised Manuscrip t received 11 DeceMber 2016)

PACS:42.25.Bs,42.25.Fx,42.79.Bh,42.79.FMDOI:10.7498/aps.66.084201

†Corresponding author.E-Mail:qizuMin@126.com

A Method to d iverge refl ected beaMun iforMly using cube-corner retrorefl ector array w ith d ihed ral ang le to lerances

Zhou Xiao-Feng Qi Zu-Min†Luo Xiang-Qian Liu Chang-An Zhu Jian-Hui Wang Ze-Hua Zhang Yi Zi Yan-Yong

(Northwest Institute of Nuclear Technology,X i’an 710024,China)

The cube-corner retroreflector(CCR)is w idely app lied in the electro-optical tracking,satellite communication,interferoMeters and ad just-free solid state laser.In soMe app lications,the incident beaMeMitted by a laser is reflected back by the CCR to a photoelectric detector.The distance between the photoelectric detector and the laser source on the ground ismuch larger than the diff raction-liMited spot.Meanwhile,the attitude angle of the CCR would randoMly vary for the jitter of the p latform.Therefore,the refl ected beaMshould be diverged uniforMly at far-field,whereas the norMal CCR cannot achieve the divergence on the reflected beam.The investigation indicated that six sub-spots are generated by a CCR w ith dihedral angle tolerances at far-field.According the characteristics of the CCR w ith dihedral angle tolerances,a structure and its design method are p roposed to diverge the refl ected beaMw ith a CCR array.The azimuthalangles of the every CCR of the array should be specially designed to generate an annu lar and uniforMpattern.Due to the p ropagation distance ismuch larger than the size of the CCR array,the feasibility of themethod is analyzed by the wave theory.A CCR array w ith a divergence half-angle of 0.5 Mrad is designed,in which the dihedral angle tolerance of every CCR is 20′′.The in fluences of the beaMand structure paraMeters on the diff raction characteristics of the refl ected beaMare investigated.The numerical results indicate the divergence half-angle of the CCR array varies quasi-linearly w ith the change of the dihedralangle tolerance,and the intensity distribution of the incident beaMdoes not influence the divergence half-angle.The propagation distance does not aff ect the uniforMity of the reflected beaMwhen the CCR array satisfies the point source condition.W hen the number of the array eleMent increases to a certain value,the increase of the number can strengthen the intensity and hard ly in fluences the uniforMity of the reflected beam.For the restriction of theMachining and assembling technics,the dihed ral angle tolerance of every CCR is hard ly identical and the assemb ling azimuthal angles of the array eleMent can not be identical w ith the design resu lt.Therefore,the influence of the assemblage azimuth error and machining accuracy of the dihedral angle are studied.It reveals that the assemb lage azimuth error does not reMarkab ly the refl ection pattern,whereas the Machining accuracy can observably aff ect the uniforMity of the reflection pattern,which can be resolved by the grow th of the number of array element.

cube-corner retroreflector,array,divergence half-angle,electro-optical tracking

10.7498/aps.66.084201

†通信作者.E-Mail:qizuMin@126.com

©2017中国物理学会C h inese P hysica l Society

http://w u lixb.iphy.ac.cn