飞秒激光烧蚀硅材料表面形成周期波纹形貌研究∗

李志明 王玺 聂劲松

(电子工程学院,脉冲功率激光技术国家重点实验室,合肥 230037)

飞秒激光烧蚀硅材料表面形成周期波纹形貌研究∗

李志明 王玺 聂劲松†

(电子工程学院,脉冲功率激光技术国家重点实验室,合肥 230037)

(2016年12月14日收到;2017年3月14日收到修改稿)

基于Sipe-Drude模型和表面等离子体激元(SPP)的干涉理论分别对单脉冲飞秒激光诱导硅表面形成低频率周期性波纹进行分析研究.探究了波长800 nm、脉宽150 fs的单个飞秒激光烧蚀硅造成不同激发水平下波纹形貌的变化,考虑到材料的光学性质变化(由Drude模型得到的介电常数变化),引入包含双温方程的电子数密度模型.计算结果表明,Sipe-Drude和SPP理论都适用于分析和解释高激发态下周期性波纹,但Sipe-Drude理论更适合分析更为广泛的周期性波纹结构.同时,波纹延伸方向总是垂直于入射激光偏振方向,其空间周期略小于激光波长,并受到入射激光通量的影响.在激光通量为0.38 J/cm2时,波纹周期达到最小值.另外,还得到了不同入射角度的波纹周期变化情况,并在不同偏振态下随入射角度增大时波纹周期呈现相反的变化趋势.该研究对于理解飞秒激光造成硅表面形成周期结构及其在加工硅材料领域具有重要参考意义.

∶Sipe-Drude模型,表面等离子体激元,低频率周期性波纹,双温方程

PACS∶52.50.JM,42.65.—k,52.38.MF,81.16.BHDOI∶10.7498/aps.66.105201

1 引 言

近20年来,超短激光对材料的烧蚀效应研究一直是热门话题,其中对超短激光造成表面周期性结构的研究更是众多专家学者一直讨论的重点对象.在激光诱导损伤过程中,飞秒激光诱导硅表面形成周期波纹结构具有重要研究意义,该结构在经典理论中被广泛认为是入射光和表面散射波之间的相互作用结果[1−5].由于飞秒激光可以很容易地诱导亚波长波纹形貌结构,且这种结构在材料着色、发光二极管和疏水材料表面的光增强等方面具有许多潜在的应用,因此受到广泛研究,以探讨其形成机理和形态控制方法.通常,这种波纹的周期(Λ)可以形成在很宽的频谱范围内,根据Λ与垂直入射的激光波长的比率,波纹类型可以分为为低频周期性结构(LSFL)(Λ/λ∼1)和高频周期性结构(HSFL)(Λ/λ≪1)[6,7].对于LSFL,认为是在高激光通量和少量脉冲条件下形成的.目前普遍接受的形成低频周期性波纹的机制是入射激光束和表面等离子体激元(SPP)之间的干涉,以及入射激光与表面粗糙度的耦合(Sipe理论)来解释激光能量沉积的现象[1],后者经过改进得到Sipe-Drude理论模型.近些年来,人们已经通过Sipe-Drude方法解释具有高斯强度分布的飞秒激光烧蚀硅表面产生的波纹和凹槽的精细形态结构,如弯曲和交叉的现象[8].Sipe-Drude模型是Spie等表面散射波理论的扩展,考虑到了由飞秒激光辐照硅表面诱导介电常数εSi变化的影响,认为在粗糙的硅表面由于入射波与表面波耦合造成能量不均匀沉积形成了低频周期性表面结构.同时,为了解释在高激光通量和少量的脉冲数量条件下低频率周期波纹的形成,一些作者提出了SPP理论.如2009年,Huang等[9]系统地描述了表面周期性结构的产生及原理,考虑到SPP的作用,将周期性结构由散射模型改为考虑等离子体的影响.2016年,Wang等[10]就飞秒激光对材料表面烧蚀的效应做了相关工作,并对偏振方向对烧蚀结果的影响进行了分析.

虽然已有关于飞秒激光烧蚀硅材料形成周期性波纹的实验及理论研究,但在理论上并未进行详细探讨,且在分析不同条件下入射激光通量及角度的影响上未给出详细解释.本文中结合Drude模型,分别对周期性波纹用Sipe-Drude和SPP两种理论并进行分析说明.但由于两种理论不能处理多脉冲时反馈阶段的作用,本文只讨论单脉冲的情况下入射激光通量及入射角度对波纹周期的影响.

2 理论模型

在极短的时间内,波纹的形成过程比凝固过程要更早完成,热力学和流体力学对波纹的形成基本不起任何作用,波纹轮廓主要是由于初始泵浦脉冲的能量沉积的不均匀性造成的.大量的带电粒子和中性硅原子从高能量沉积的区域喷射,形成波纹结构的凹槽,因此,波纹主要在几百皮秒内形成.而激光诱导光电离在几十个皮秒内完成,所以这里要考虑到激发自由载流子的情况.

2.1 电子数密度模型

基于双温方程描述飞秒激光烧蚀硅材料激发自由载流子涉及双光子吸收、电子扩散、俄歇复合等复杂过程[11].电子密度Ne方程可写为

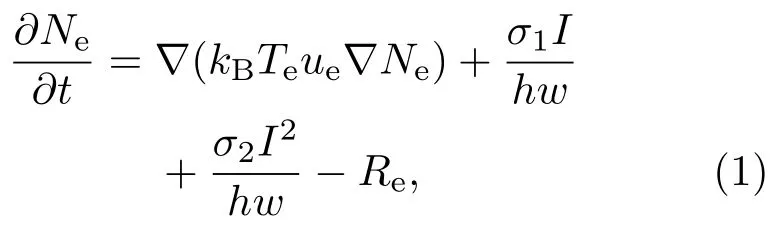
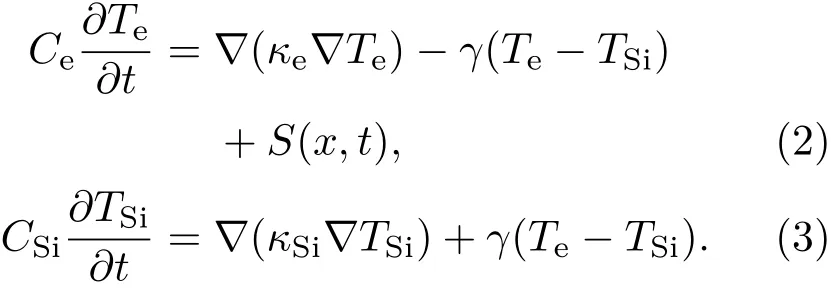
硅的初始温度为300 K,激光光源项为[12]

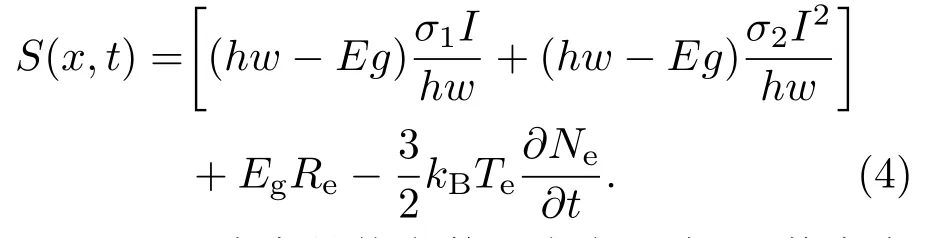
(2)—(4)式中具体参数及定义见表1,其中自由载流子吸收被忽略.

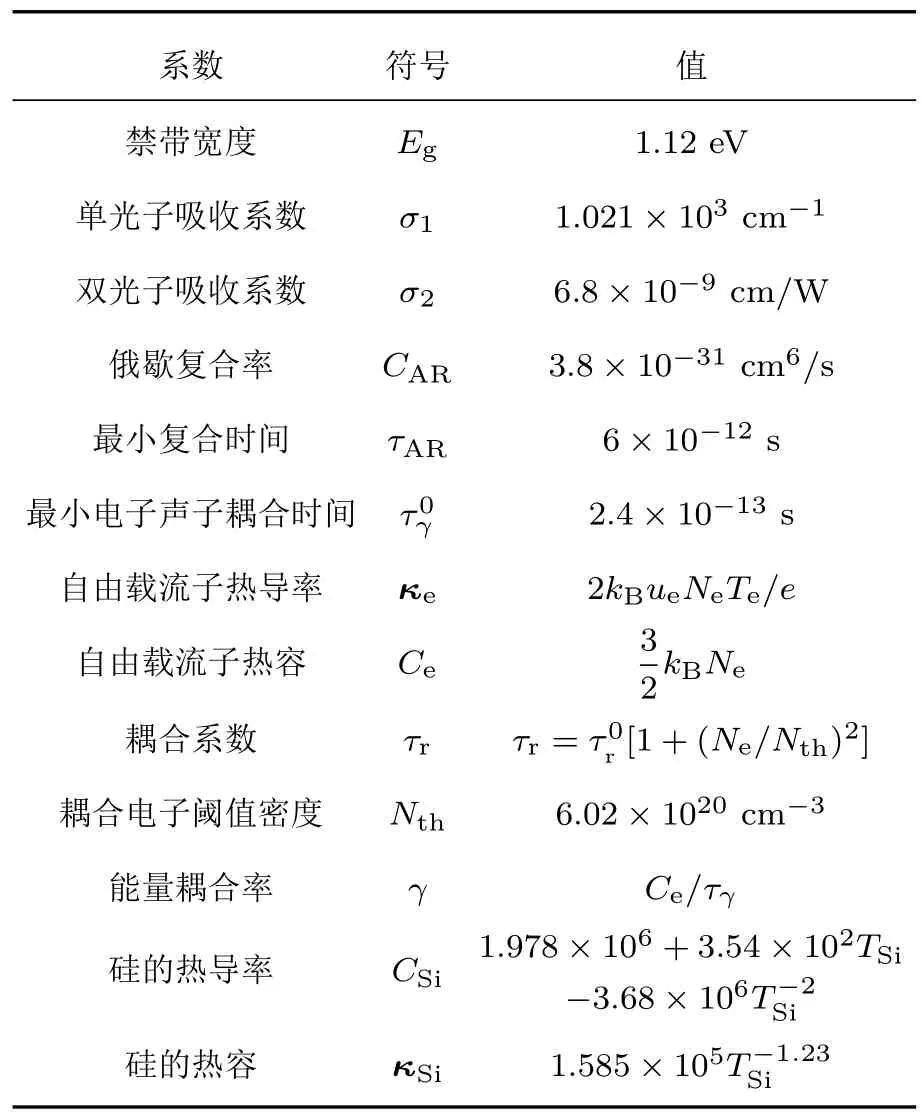
表1 双温方程参数[9]Table 1.Two-temperature equation’parameters.

在临界电子密度之上,虽然能量吸收受表面反射率的限制,但高于该限度时自由载流子的数量仍然由于自由载流子的高温吸收而增加,导致扩散传输和碰撞电离之间的相互作用.

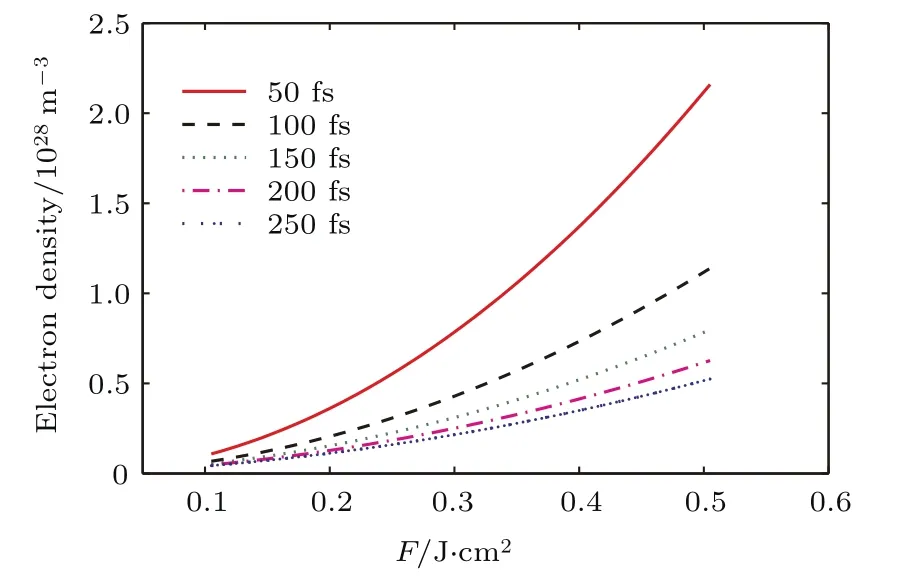
图1 (网刊彩色)最大激发电子数密度随激光通量的变化Fig.1.(color online)Maximum of the electron density during the interaction as a function of laserfluence.

图1为不同脉宽飞秒激光辐照下硅表面产生的最大等离子体密度随能量的变化.超短脉冲作用下,最大电子浓度随激光通量的增加呈非线性变化,这是因为硅的自由载流子吸收取决于具有临界条件下的自由载流子密度.在本文中主要考虑脉宽为150 fs时的电子浓度变化,引入Drude模型,硅的介电常数可以表示为电子密度和入射激光频率的函数∶

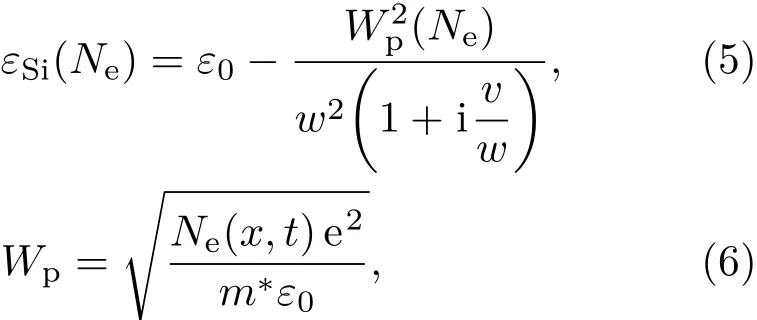
其中,ε0为常态下硅的介电常数,w为入射激光的角频率,wp为等离子体频率,电子的有效质量m∗=0.18me,v=1.1×10−15为阻尼系数[13].

如果激光脉冲能量足够大,则硅表面根据能量沉积轮廓熔化,在再凝固时产生特定的表面图案(周期性波纹).图2为Sipe-Drude和SPP两种模型下模拟周期性表面结构的形成的示意图.

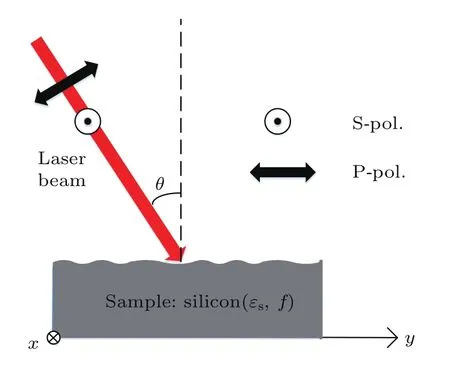
图2 激光入射到粗糙的几何表面示意图Fig.2.Geometry of the laser beam incidence to a rough surface.

2.2 Sipe-Drude理论

Sipe-Drude理论详细地阐述了飞秒激光激发硅表面周期性波纹的形成机理,其引入了Sipe等人的理论,建立在入射光与表面散射的电磁场的干涉理论上,即飞秒激光光波在表面缺陷或表面粗糙度上的散射形成非共振激发.因此,材料粗糙表面下的不均匀吸收导致波纹(LIPSS)形成[12].Sipe理论的优点是能够在空间频域中预测硅表面上的不均匀能量沉积,其通过称为效率因子η的标量函数进一步量化(其中η(k)是在空间频率k处的表面粗糙度引起不均匀能量沉积的功效因子),b(k)代表k处表面粗糙度的傅里叶振幅分量,所以Sipe理论数学表达式为|η(k)|×|b(k)|.由于b(k)是变化缓慢的函数,可以忽略不计,所以在k处的η的局部最大值决定了其波纹周期特性.如图3所示意,入射激光在S偏振方向上,以角度θ入射粗糙硅表面,根据文献[14]((1)—(14)式)可以从最初的Sipe模型中得到功效因子η(k)作为周期性波纹波矢量κx和κy的函数.并在文献[1]中,根据假设的球形面,采用通常的s=0.4和f=0.1值作为表面粗糙度.

图3 功效因子η(k)作为波矢量κx和κy的函数随激光通量变化的二维归一化灰度图 (a)0.1 J/cm2;(b)0.3 J/cm2;(c)0.5 J/cm2;(d)0.7 J/cm2Fig.3.2D gray scale maps of the efficacy factor η(k)as a function of the wave vector κxand κywith the change of laserfluence:(a)0.1 J/cm2;(b)0.3 J/cm2;(c)0.5 J/cm2;(d)0.7 J/cm2.

在Sipe-Drude理论中,介电常数受激发的电子数密度影响.图3为功效因子η(k)随激光入射通量的变化的二维灰度图,偏振方向为水平方向κx,激光通量为0.1—0.7 J/cm2,在κx方向上的B区域(与偏振方向平行)形成近周期性波纹,波纹方向垂直于偏振方向.由图3(a)—(c)可以发现,该方向上的波纹结构曲线越来越明显.为了更直观地比较入射能量和角度的影响,我们定量计算了水平横截面κx的功效因子η(k)的最大值变化(κy=0).如图4所示,随着电子数密度的变化,功效因子η(k)的最大值变化先增后减(内插图为激光通量变化下的情况),在电子浓度为5.27×1021cm−3时出现局部区域最小值,此时的介电常数Re(εSi)=−1.在电子浓度约6×1021cm−3,即0.42 J/cm2时达到最大值,同时在一定的激光通量下,定义低频波纹周期的最大值为Λpeak=λ/κx(LSFL)[1],其中功效因子最大值对应波矢量κx,Λpeak可以作为定性分析波纹周期变化的值.当激发电子数密度大于1.16×1022cm−3(激光通量大于0.6 J/cm2)时,硅处于高激发态,Sipe-Drude理论预测表征低频周期波纹的特征峰值急速下降,对应的κx值接近1,周期快速增大并将接近于入射光波长.如图3(d)所示,当再进一步增大激光通量,激发更多的自由载流子,此时低频周期性波纹很难再观察到.

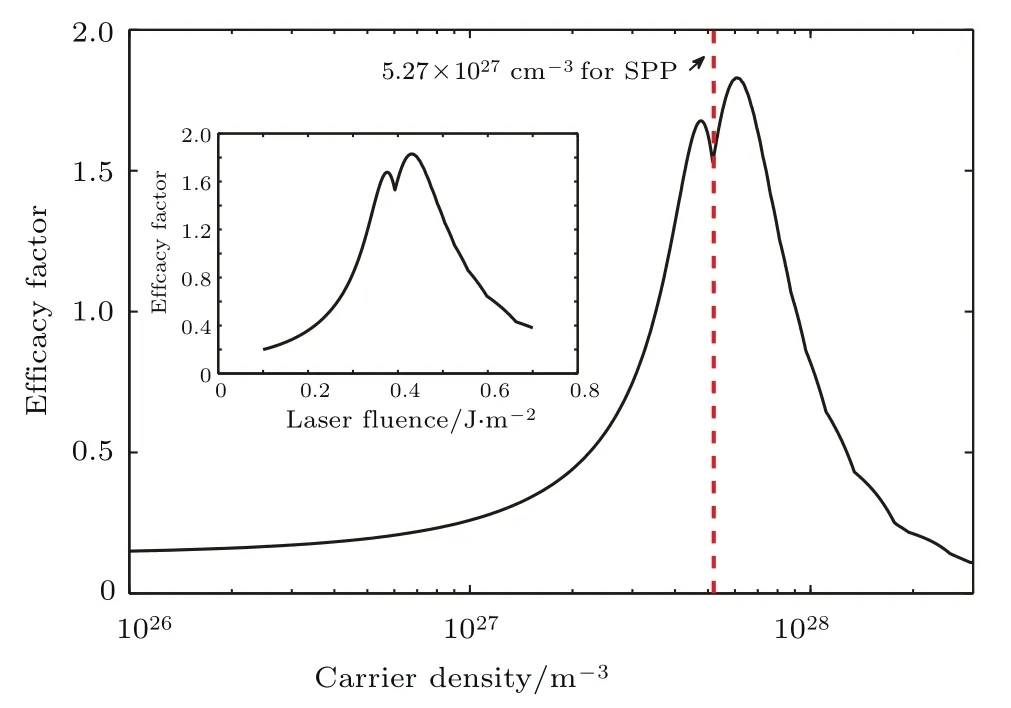
图4 功效因子最大值随硅材料激发程度的演化Fig.4.The efficacy factor as a function of the excitation levelof the laser-excited silicon.

2.3 SPP理论

虽然硅是非激发态的半导体(介电常数为13.65+0.048i[14])且表面等离子体激元只可能在电介质和金属的界面激发.但在高通量激光辐照下产生高浓度电子数,硅的介电常数实部可以降到−1以下∶

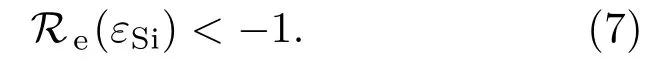
在800 nm、150 fs的激光作用下,阈值电子数密度为5.23×1021cm−3,对应图1,得到0.426 J/cm2为硅材料表面产生等离子体的临界阈值通量.飞秒激光诱导光电离为介电函数提供自由载流子变化的过程等效于瞬时掺杂,因此,入射光与表面等离子体激元耦合是有可能的,SPP理论上指出传播的表面等离子体偏振子波与入射光在硅-电介质界面处干涉,在高激发态的硅表面形成波纹周期性,并可以用以下公式近似表达∶

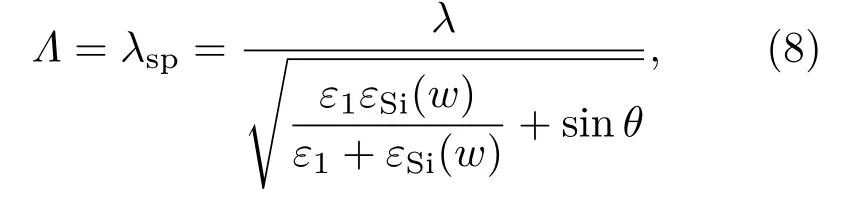
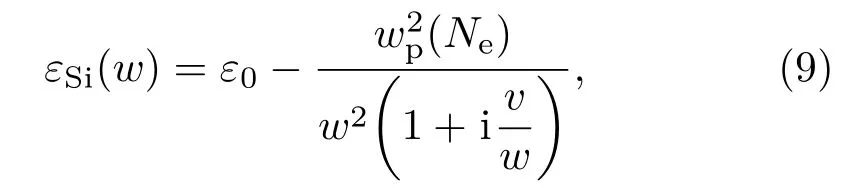
其中,ε1和εSi(w)是硅表面两侧的介电常数,ε1=1为空气中的介电常数.图5为在垂直入射的情况下(θ=0◦),激光通量为0.45—0.8 J/cm2范围的波纹周期变化情况.在高激发态下,随着激光通量增大,波纹周期增大,且接近激光波长.

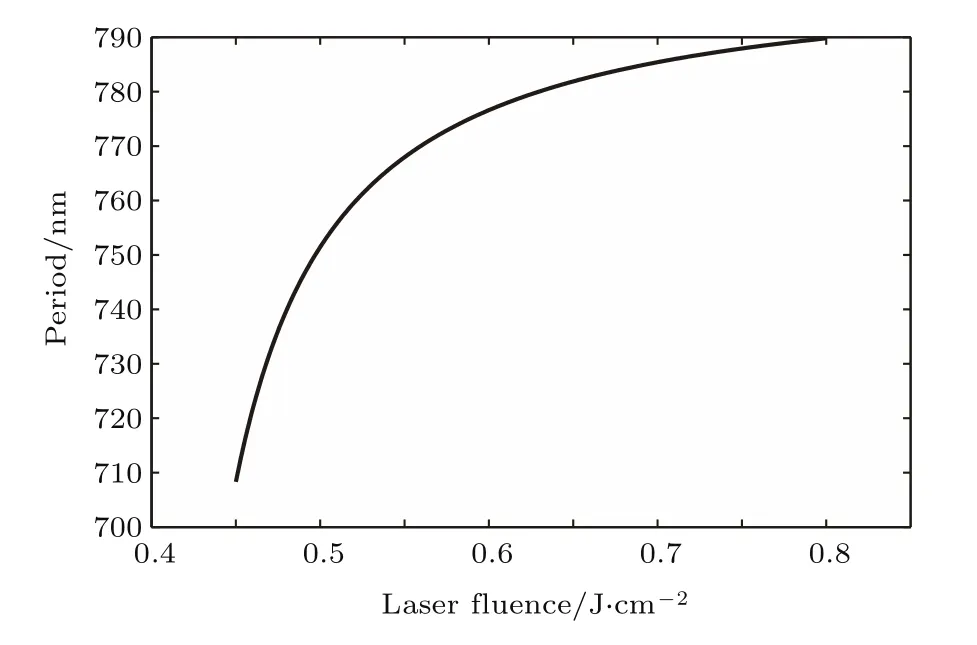
图5 波纹周期随激光通量的演化Fig.5.Evolution of period with laserfluence.

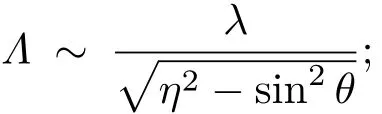
3 结果与讨论

图6为S偏振方向下,入射角度θ取0◦,30◦,45◦时功效因子η(k)函数的二维归一化分布图.垂直方向上存在两个表征周期性波纹的功效因子局部最大值,从图6(a)—(c)可见,水平B区域方向上对应的功效因子最大值(对称的镰刀形局部最大值)降低,波纹形貌越发不明显.如图7(a)所示,不同激发水平下诱导的波纹周期随入射激光通量增加呈现先减小后增大的趋势,在约0.38 J/cm2,入射角度为0◦时,达到最小值730 nm,对应的电子浓度可由Re(εSi)=0得到Nth=4.92×1021cm−3.图7(b)表示的是入射P偏振方向时波纹周期随入射激光通量的演化图,可以发现波纹周期具有相同的变化趋势,最小值对应的通量同样在0.38 J/cm2.此外,由图6可以看到,随入射角度增大,功效因子最大值对应的波数κx减小,而κy增大,这也解释了两种不同偏振方向的波纹周期呈相反趋势变化,如图7(a)和图7(b)所示.

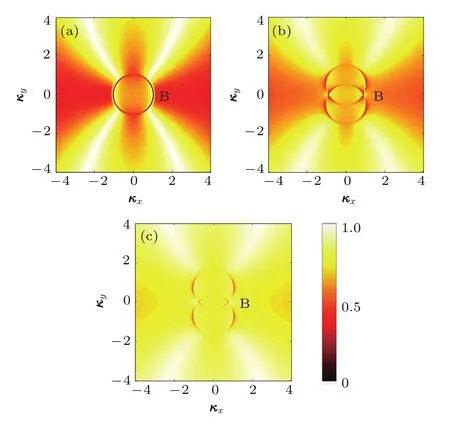
图6 (网刊彩色)功效因子η(k)作为波矢量κx和κy的函数随入射角度变化的二维归一化分布图 (a)0◦;(b)30◦;(c)45◦Fig.6.(color online)2D scale maps of the efficacy factor η(k)as a function of the wave vector κxand κywith the change of angle of incidence:(a)0◦;(b)30◦;(c)45◦.

为了更直观地了解入射角度和激光偏振方向对波纹周期性的影响,图8给出了在激发电子数密度为6×1021cm−3时,低频周期性结构在不同偏振方向上随入射光角度增大的变化情况.可以看出,两种理论计算的结果近似相同,在S偏振方向上随入射角度增大波纹周期递减,在45◦时周期达到约425 nm,而在P偏振方向上随入射角度增大波纹周期递增,在45◦时周期达到约1050 nm.

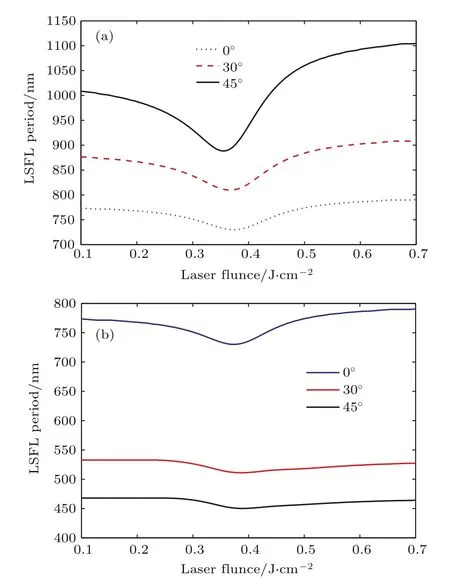
图7 (网刊彩色)低频波纹周期随入射激光通量的演化(a)S偏振;(b)P偏振Fig.7.(color online)Evolution of LSFL period with laserfluence:(a)S-polarization;(b)P-polarization.

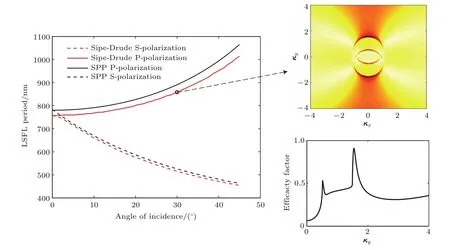
图8 (网刊彩色)低频周期结构随入射光夹角及偏振的变化Fig.8.(color online)LSFL periodicity as a function of angle of incidence and laser polarization.

其中30◦所示的P偏振方向上功效因子η(k)二维分布图如图8右上图所示,发现其波纹分布强度正好与S偏振方向相反,主要集中在κy方向上.同时在该图下方我们给出了κy方向上功效因子η(k)的一维分布图(κx=0)(图8右下图),图中曲线上存在两个峰值,且第二个峰值的数值更大,其大小决定了波纹的周期范围.应当指出,实际过程中,消融坑的内壁实际上是连续弯曲的表面结构,因此几乎每个部分的弯曲表面不仅具有S偏振光与表面的相互作用,而且具有P偏振光与表面的相互作用.此外,由于初始脉冲在粗糙表面能量的不均匀沉积造成倾斜的波纹壁,以致实际入射角度增大,从而引起波纹周期性不断变化,在本文中主要考虑单脉冲作用的结果,所以单独在S偏振方向讨论波纹形貌的方法是可行的.

4 结 论

基于Sipe-Drude理论和SPP理论分别对单脉冲飞秒激光诱导硅表面形成低频率周期性条纹进行了分析讨论.研究表明∶1)两种理论都适用于激发高等离子体浓度的情况,Sipe-Drude理论可以进行广泛的周期性波纹结构分析;2)周期性波纹主要出现在垂直于偏振方向上;3)当入射激光造成损伤时诱导的电子数密度远大于激发SPP的临界电子密度(约大于1.16×1022cm−3),表征周期性波纹的最大功效因子对应的波数κx接近1,此时波纹显示出比激光波长稍小的空间周期性;4)两种理论都很好地模拟了不同入射角度下周期性波纹的变化情况,得到不同偏振态下,随入射角度增大,波纹周期呈相反的变化趋势.

[1]Sipe J,Young J,Preston J,van Driel H 1983 Phys.Rev.B 27 1141

[2]Bonse J,Kruger J 2010 J.Appl.Phys.108 034903

[3]Li Z C,Zheng J,Ding Y K,Yin Q,Jiang X H,Li S W,Guo L,Yang D,Wang Z B,Zhang H,Liu Y G,Zhan X Y,Tang Q 2010 Chin.Phys.B 19 125202

[4]Zhang N,Bao W X,Yang J H,Zhu X N 2013 Chin.Phys.B 22 054209

[5]Zhang W,Teng H,Shen Z W,He P,Wang Z H,Wei Z Y 2016 Acta Phys.Sin.65 224204(in Chinese)[张伟,滕浩,沈忠伟,何鹏,王兆华,魏志义2016物理学报65 224204]

[6]Dufft D,Rosenfeld A,Das S,Grunwald R,Bonse J 2009 J.Appl.Phys.105 034908

[7]Liang F,Valle’e R,Chin S 2012 Opt.Express 20 4389

[8]Bonse J,Rosenfeld A,Kruger J 2009 J.Appl.Phys.106 104910

[9]Huang M,ZhaofL,Cheng Y 2014 J.Appl.Phys.115 103102

[10]Wang C W,Zhao Q Z,Zhang Y,Wang G D,Qian J,Bao Z J,Li Y B,Bai F,Fan W Z 2015 Acta Phys.Sin.64 0205204(in Chinese)[王承伟,赵全忠,张扬,王关德,钱静,鲍宗杰,李阳博,柏锋,范文中 2015物理学报 64 0205204]

[11]Bulgakova N,Stoian R,Rosenfeld A,Hertel I,Marine W,Campbell E 2005 Appl.Phys.A 81 345

[12]Derrien T,Krüger J,Itina T,Höhm S,Rosenfeld A,Bonse J 2013 Opt.Express 21 29643

[13]Sokolowski T,Linde D 2000 Phys.Rev.B 61 2643

[14]Bonse J,Munz M,Sturm H 2005 J.Appl.Phys.97 013538

PACS∶52.50.JM,42.65.—k,52.38.MF,81.16.BHDOI∶10.7498/aps.66.105201

*Project supported by the Foundation of the State Key Laboratory of Pulsed Power Laser Technology of China(Grant No.SKL2014ZR03).

†Corresponding author.E-mail:njs7001@sina.com

Formation of periodic ripples on silicon surface ablated by femtosecond laser∗

Li Zhi-Ming Wang Xi Nie Jin-Song†
(State Key Laboratory of Pulsed Power Laser Technology,Electronic Engineering Institute,Hefei 230037,China)

14 December 2016;revised manuscript

14 March 2017)

The formation mechanism of low-spatial-frequency laser-induced periodic surface structure(LSFL)on singlecrystalline silicon irradiated by single femtosecond-laser pulse(pulse duration τ=150 fs and central wavelength λ=800 nm)in air is investigated theoretically based on the interference theory of Sipe-Drude model and surface plasmon polariton(SPP).In order to account for transient intrapulse changes in the optical properties of the material due to the excitation of a dense electron-hole plasma,we model the maximum of the electron density as a function of laserfluence by solving the generally accepted two-temperature equation and Drude model.The results show that both theories are applicable to explaining the LSFL formation on the high-excited silicon.In the Sipe-Drude theory,the factor η(k)is used to describe the efficacy with which the surface roughness at position k leads to inhomogeneous absorption of radiation.Wefind that the value of η(k)first increases until reaching a maximum at an electron density of 6×1021cm−3and then decreases with the laserfluence increasing.When the incident laserfluence is 0.38 J/cm2,which is the threshold for excited plasma,the period reaches a minimum value in a small range of the top.Besides,the law of period is calculated according to the relationship between the η(k)and period.In the SPP theory,the ripple period on the highly excited silicon increases with the laserfluence increasing.Comparing the scopes of application of two theories,the Sipe-Drude theory is found to be suitable for the analysis of more extensive periodic surface structures,while the SPP theory is applicable only for the case that laserfluence is close to the damage threshold.Moreover,our results are capable of explaining that the delay direction of periodic ripples are always perpendicular to the incident laser polarization direction by using the Sipe-Drude theory.When laserfluence approaches to the damage threshold,the LIPSS period is calculated sightly to be below the laser wavelength.It also reveals that the periodic surface structures are approximately the same in the different polarization directions with the increase of incident angle.Taking into account a single pulse,the corrugation period decreases with the increase of angle of incidence in the S polarization direction.And under different polarizations,with the increase of incident angle,the changes of the ripple period show an opposite trend.The obtained dependence provides a way to better control the properties of the periodic structures induced by femtosecond laser on the surface of a semiconductor material,which is of great significance for understanding the formation of periodic structure of silicon surface,caused by femtosecond laser,and its application in the field of silicon materials processing.

∶Sipe-Drude model,surface plasmon polariton,low-spatial-frequency laser-induced periodic surface structures,two-temperature equation

∗脉冲功率激光技术国家重点实验室基金(批准号:SKL2014ZR03)资助的课题.

†通信作者.E-mail:njs7001@sina.com

©2017中国物理学会Chinese Physical Society