掺杂硅纳米梁谐振频率的理论模型及分子动力学模拟∗

马霞 王静

(新疆大学物理科学与技术学院,乌鲁木齐 830046)

掺杂硅纳米梁谐振频率的理论模型及分子动力学模拟∗

马霞 王静†

(新疆大学物理科学与技术学院,乌鲁木齐 830046)

(2016年12月23日收到;2017年2月28日收到修改稿)

通过理论计算与模拟,研究分析了P元素替代掺杂单晶硅纳米梁的谐振频率.计算模拟了两端固支单晶硅纳米梁的谐振频率随尺寸、掺杂浓度与温度的变化.通过对计算结果与模拟结果的分析得到∶单晶硅纳米梁的谐振频率随着硅纳米梁长度尺寸的增大而减小;硅纳米梁的谐振频率随着掺杂浓度的增大而增大,但变化趋势并不明显;最后考虑了温度效应,发现掺杂硅纳米梁的谐振频率随着温度的增大而减小,但从谐振频率的数值来看,硅梁的谐振频率随温度的变化趋势并不明显,即温度对硅梁谐振频率基本无影响.由此得出结论∶掺杂浓度与温度对硅纳米梁谐振频率的影响很小,影响单晶硅纳米梁谐振频率的主要因素是尺寸大小,掺杂单晶硅纳米梁的谐振频率具有尺寸效应.

∶单晶硅纳米梁,谐振频率,掺杂,温度

PACS∶61.72.uf,62.25.—g,81.40.JjDOI∶10.7498/aps.66.106103

1 引 言

随着纳机电系统(NEMS)的研究和发展,其在很多领域有了越来越多的应用,如超高精度传感器[1]、超大规模传感器[2−4]、开关[5]、高频谐振器等[6].作为基础结构的单晶硅纳米梁,其力学性能如杨氏模量和谐振频率的研究是非常重要的,受到了众多研究人员的重视.

文献[7]在2003年就已在实验上测量得到了超薄硅悬臂梁的杨氏模量及谐振频率的尺寸效应;基于Sun和Zhang[8]提出的计算简单立方晶格杨氏模量的半连续模型,Bao等[9,10]研究了硅纳米的载荷挠度与谐振频率;2008年,Wang等[11]用半连续模型计算研究了温度以及厚度对单晶硅纳米薄膜杨氏模量的影响;2015年,吕焕玲和王静[12]用基于Keating形变势的半连续体模型研究了掺杂浓度与厚度对单晶硅纳米薄膜的杨氏模量的影响.此外,一些研究人员用分子动力学方法研究了硅纳米结构的力学特性,如Gong等[13]用分子动力学模拟研究了硅纳米片的杨氏模量;Cao等[14]与Pishkenari小组[15]均用分子动力学方法模拟计算了硅纳米线的谐振频率,得到了谐振频率的尺寸效应.2016年,吕焕玲和王静[16]通过分子动力学模拟研究了300 K下掺杂浓度以及长度尺寸对掺杂硅纳米梁谐振频率的影响,发现掺杂浓度对硅纳米梁谐振频率的影响很小,而影响硅纳米梁谐振频率的主要因素是梁的尺寸.

无论是从基础研究的角度,还是着眼于未来的器件应用,研究掺杂单晶硅纳米结构的力学特性具有重要的意义.本文分别采用半连续模型与分子动力学方法计算模拟了掺杂浓度、尺寸以及温度对[100]方向双端固支单晶硅纳米梁谐振频率的影响.

2 基于半连续模型的掺杂硅纳米梁谐振频率的计算与分析

本文研究的是磷原子替代掺杂硅晶胞体对角线四分之一处的硅纳米梁结构,掺杂磷原子的硅晶胞如图1所示.

本文讨论掺杂浓度分别为30×1020,15×1020,7.5×1020,3.75×1020cm−3,横截面积S为16A×16A,长度尺寸L从40A到60A(长度尺寸变化间隔∆L=4A,其中A为硅晶胞的晶格常数,A=5.432)的硅纳米梁在不同温度时的谐振频率.

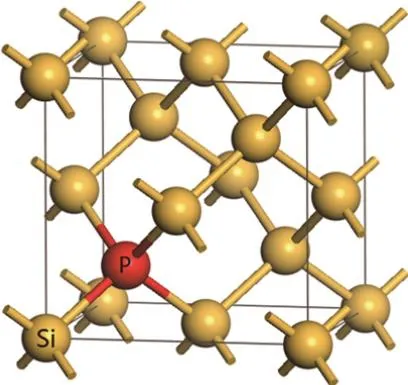
图1 (网刊彩色)体对角线四分之一处掺杂磷元素硅晶胞示意图Fig.1.(color online)Doping P atom at a quarter of body diagonalof the Silicon crystal cell.

2.1 谐振频率的计算

微米及以上尺寸的材料主要采用基于长波假设的连续介质模型研究材料的物理性能,当材料的尺寸进入纳米级时,纳米尺度材料与宏观尺度材料的结构相比,纳米结构展现出了一些优异的力学效应.同时,连续介质模型已无法直接应用于纳米结构中,需要建立一种连续介质模型与原子模型相结合的模型来研究纳米尺度材料的物理性能.2003年,Sun和Zhang[8]从原子之间的相互作用力出发,建立了对简单立方晶格的杨氏模量进行研究的一种理论方法——半连续模型.半连续模型在符合长波假设的方向仍然使用连续介质模型来研究,在纳米尺寸方向从原子出发来研究.若研究对象为硅纳米梁时,半连续模型考虑的厚度与宽度方向从原子出发研究,由于长度方向连续,所以仍用连续介质模型进行研究.

由半连续模型出发,文献[12]得到在体对角线四分之一处替代掺杂P原子的硅晶胞的形变能UP与纯硅晶胞的形变能USi,即

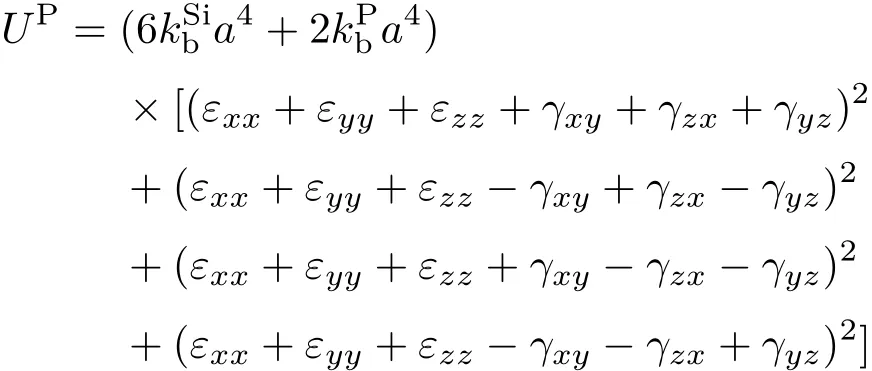
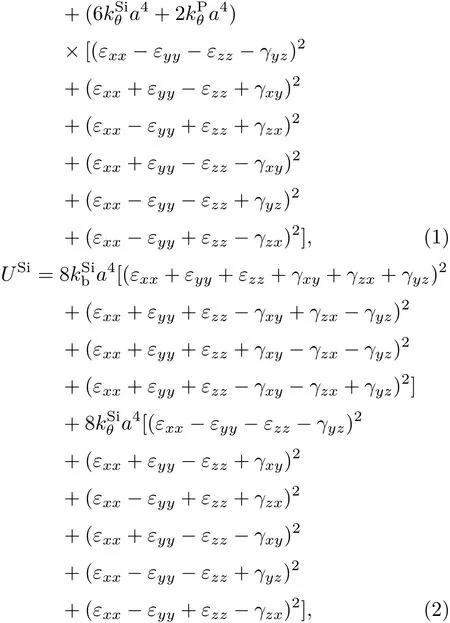
当温度升高时,物体的热运动就会加剧,随之原子在平衡位置的振动幅度就会增大.由于原子在平衡位置两侧的受力本来就不对称,且受力不对称的这种情况随着温度的升高变得越来越显著,从而导致相邻原子之间的距离增加,晶体膨胀晶格常数增加.因此体系内原子与原子之间的键长发生变化,原子与原子之间的键长rij随着温度的增大而增大.由非谐Keating形变势模型[17]可知kb为键长的幂函数,kθ为键长与键夹角的幂函数,即幂函数形式如下∶

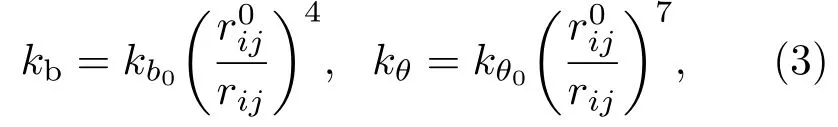
假设硅纳米梁的厚度方向与宽度方向均有N层硅晶胞,由于这两个方向的不连续性,需要从晶胞中原子的厚度出发[19],那么硅纳米梁的厚度与宽度均可表示为h=(4N+1)a.由于硅纳米梁长度方向是连续的,利用长度方向的对称性与周期性,可选择长为一个晶胞,厚度与宽度与硅梁相同的结构作为一个计算单元,则硅纳米梁计算单元的体积可表示为V=4(4N+1)2a3.当硅纳米梁的掺杂浓度为α时,硅纳米梁计算单元的形变能U可表示为

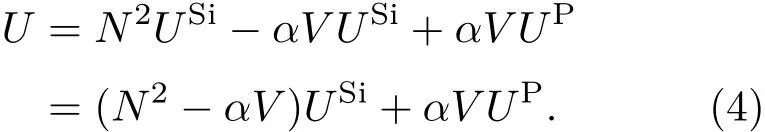
将(1)式与(2)式代入(4)式可得

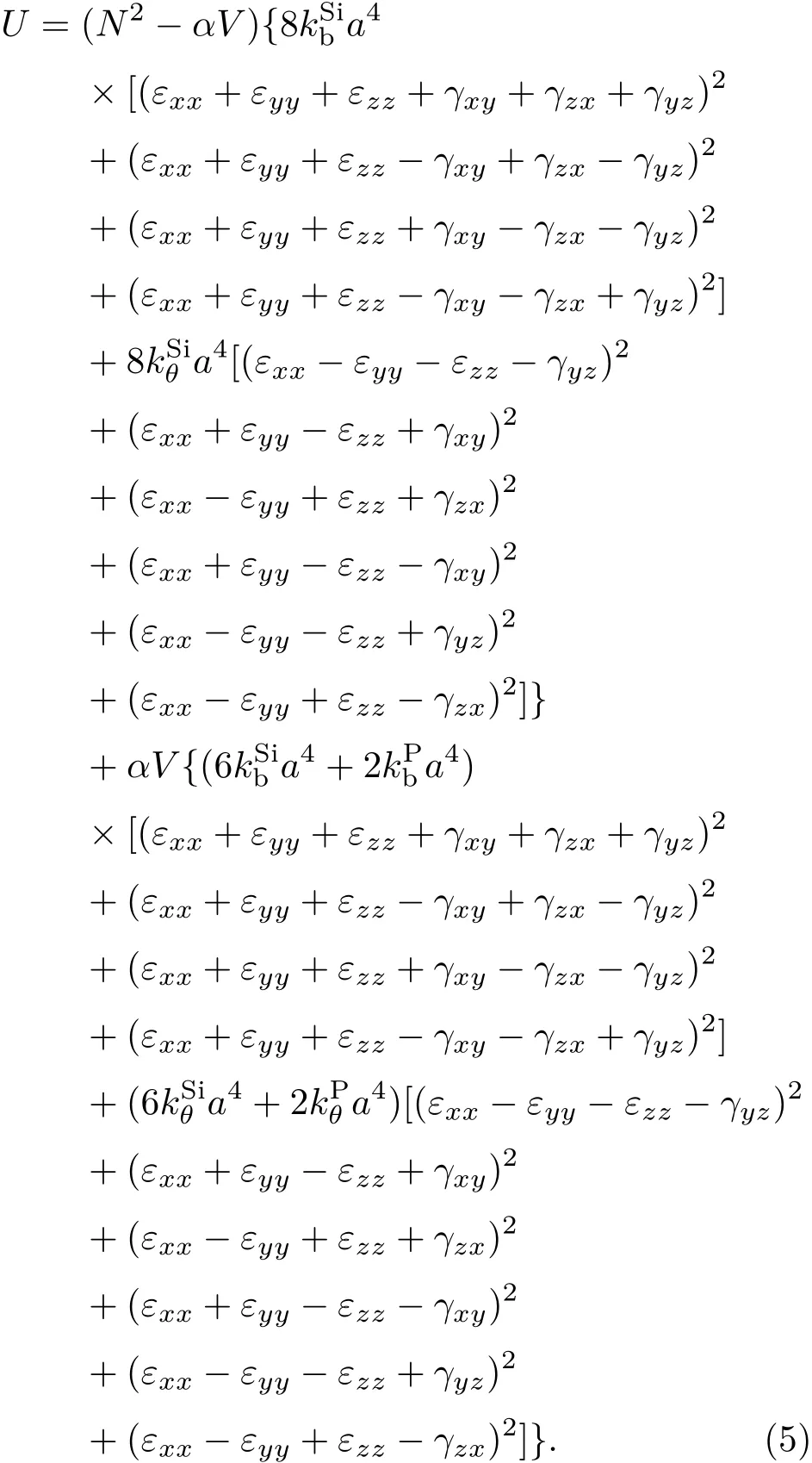
那么硅纳米梁计算单元的形变能密度u表示为

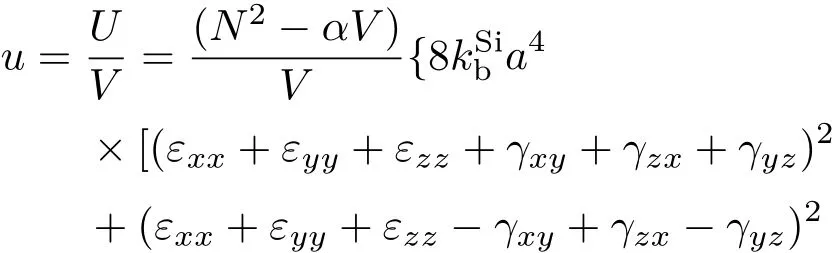
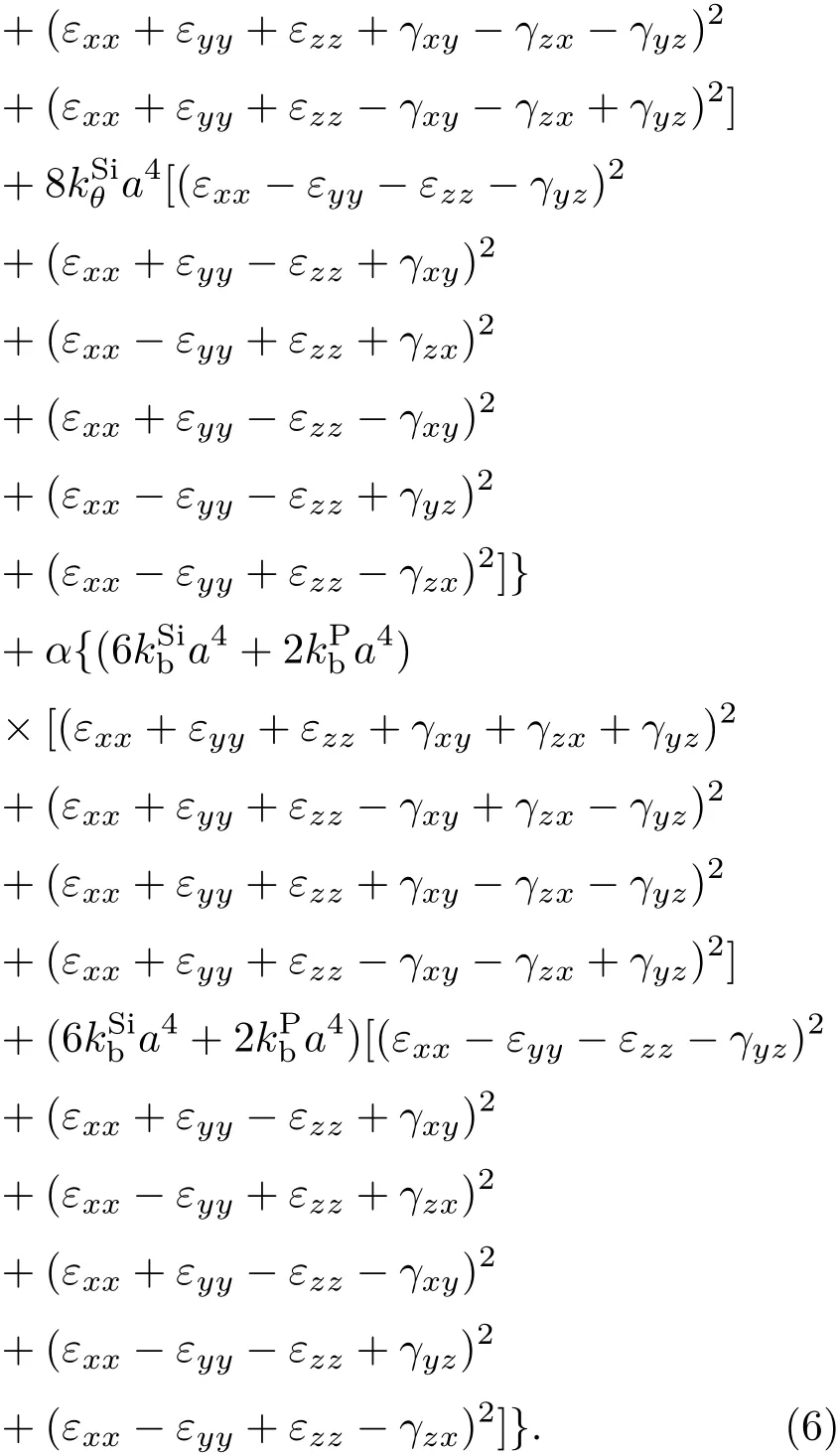
长度为L的单晶硅纳米梁在振型w(x)和频率为ω的条件下进行自由振动时,具有一定的瞬时挠度,梁的瞬时挠度公式可表示为下式[10]

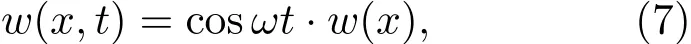
其中w(x)为梁的挠度函数,且

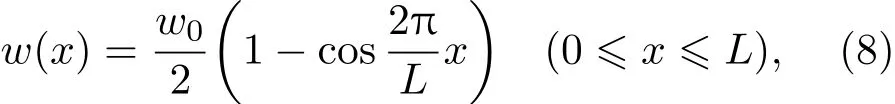
其中w0为硅纳米梁中点的最大挠度值.硅纳米梁在振动过程中,不考虑其他能量耗散遵循机械能守恒,最大的动能Kmax表示为

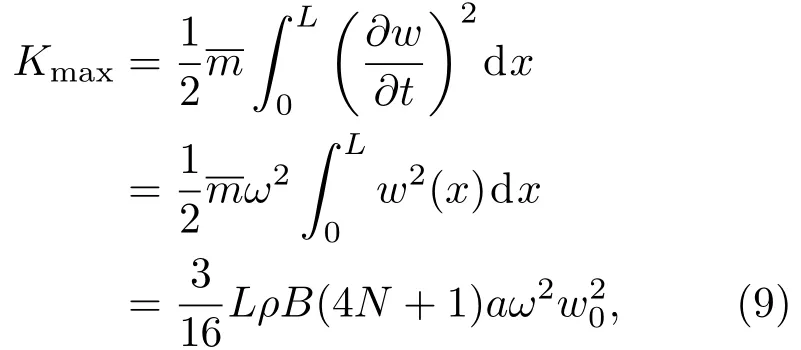
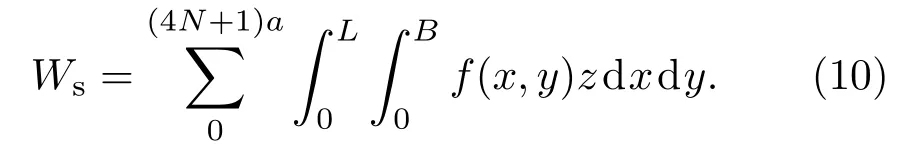
将(6)式代入(10)式得到掺杂硅纳米梁的应变势能

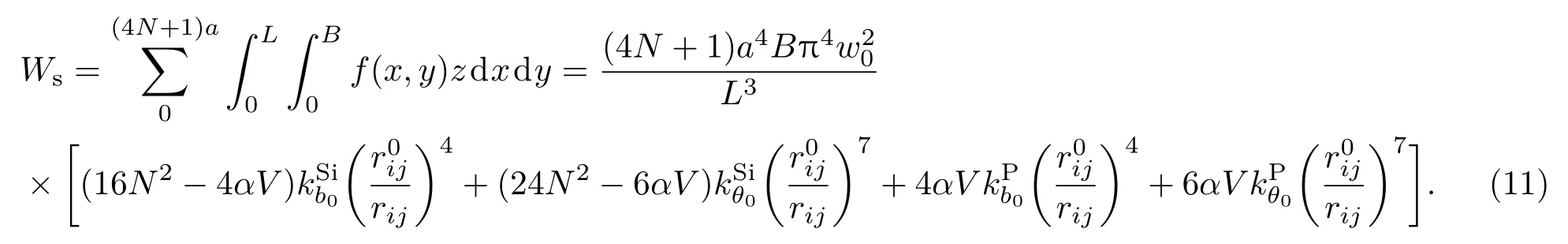
根据机械能守恒可知WS=Kmax,即可得到下式∶

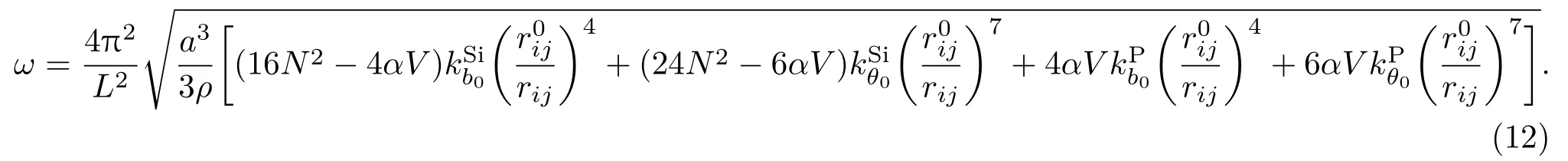
由谐振频率f=ω/2π,可得到掺杂硅纳米梁谐振频率的解析式∶

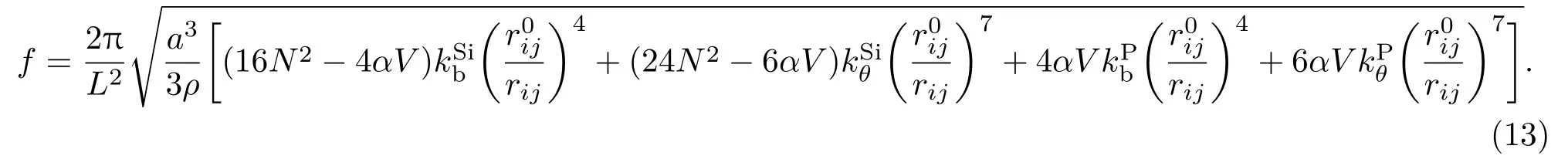
由谐振频率的解析式可以看出,硅梁的谐振频率随着长度尺寸的增大而减小,随着键长的增大而减小,由于键长随着温度的增大而增大,即硅梁的谐振频率随着温度的增大而减小.

2.2 计算结果与讨论

当掺杂浓度为7.5×1020cm−3,横截面积S=16A×16A时,不同长度硅梁的谐振频率随温度的变化曲线如图2所示,其中键长随温度的变化采用文献[21]的结果.由图可以看出,随着温度的增大,硅纳米梁的谐振频率逐渐减小,但是减小的趋势不明显,几乎呈现的是一条平线,即温度对硅纳米梁的谐振频率几乎不影响.其次,从图中还可以看出,随着硅纳米梁长度的增加,硅纳米梁的谐振频率减小,并且每个长度之间的谐振频率的数值的间隔是逐渐减小的,也就是说,硅纳米梁的谐振频率随着长度的增大而减小的趋势并不是呈现线性减小,而是随着长度的增大,硅纳米梁的谐振频率减小的趋势逐渐减小,此结果与文献[22]基于共振频率表达式拟合的理论曲线趋势是一致的.由振动频率的求解式f=1/T(T为振动周期)可知,振动频率与振动周期成反比关系,由于梁的长度越长,振动越慢,则振动的周期越大,周期越大时频率越小,所以硅梁的谐振频率随着长度的增大而减小.

当长度L=60A,横截面积S=16A×16A时,不同掺杂浓度的硅纳米梁的谐振频率随温度的变化曲线如图3所示.

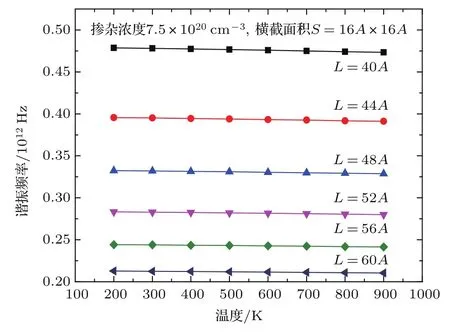
图2 (网刊彩色)不同长度硅梁的谐振频率随温度的变化Fig.2.(color online)The resonance frequency of the silicon nano-beam as a function of the temperature and the length.

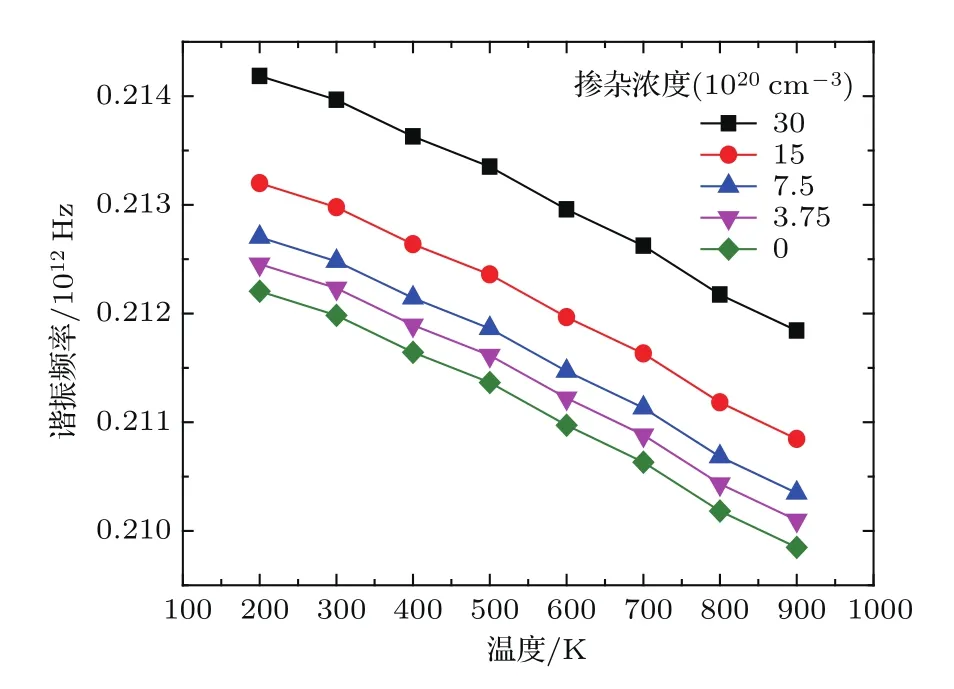
图3 (网刊彩色)不同掺杂浓度的硅纳米梁的谐振频率随温度的变化Fig.3.(color online)The resonance frequency of the silicon nano-beam as a function of the temperature and the doping concentration.

由图3可知,当硅纳米梁的长度以及横截面积一定时,硅纳米梁的谐振频率随着温度的升高逐渐减小,但是从谐振频率的数值来看,谐振频率随着温度的增大减小的值非常小,减小的趋势基本呈线性,此结果与文献[23]所得结果的趋势相同.当温度与尺寸一定时,硅梁的谐振频率随着掺杂浓度的增大而增大,从图3中可以看到,随着掺杂浓度之间间隔的逐渐增大,不同掺杂浓度的谐振频率之间的间隔也在逐渐增大.但从(0—7.5×1020— 15×1020cm−3)以及(0—15×1020—30×1020cm−3)这两个等掺杂浓度间隔的序列,可以看出同一温度且掺杂浓度间隔相同时谐振频率的增量在减小.因此,谐振频率与掺杂浓度并不是简单的线性关系,这也与谐振频率的解析(13)式所呈现的关系是一致的.

3 掺杂硅纳米梁谐振频率的分子动力学模拟

3.1 建立模型

分子动力学方法是一种计算机模拟实验方法,是研究凝聚态系统的有力工具.该方法不仅可以得到原子的运动轨迹,还可以观察到原子运动过程中的各种微观细节,它是对理论计算和实验的有力补充.本文应用计算机软件Material Studio(MS)中的Forcite模块通过分子动力学方法模拟分析了掺杂浓度、长度尺寸与温度对单晶硅纳米梁谐振频率的影响.

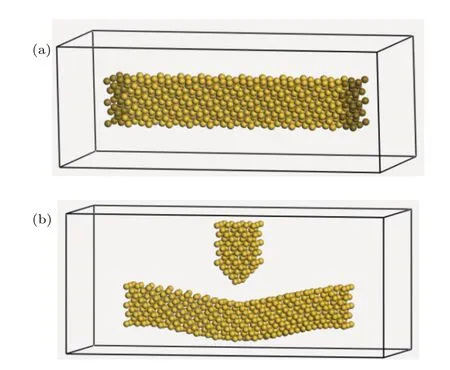
图4 (网刊彩色)(a)双端固支硅纳米梁;(b)结构优化后的硅探针结构与硅纳米梁Fig.4.(color online)(a)A double-clamped Sinanobeam;(b)a silicon probe and a silicon nano beam after optimization.

分子动力学模拟的双端固支单晶硅纳米梁如图4(a)所示.按照不同的浓度与不同长度尺寸对单晶硅纳米梁进行掺杂建模,将建好的模型进行切割建立真空层,之后将一个由硅原子构建的探针形状的结构放置在纳米梁正上方并将其固定(硅探针结构也在真空层内),之后对硅纳米梁进行结构优化,由于硅探针结构与纳米梁之间存在范德瓦耳斯力,所以结构优化后硅纳米梁发生弯曲如图4(b)所示.由于优化后的硅纳米梁是弯曲的,所以将硅探针结构去掉之后分子动力学模拟的硅纳米梁做自由振动运动.在NVE系综下用模拟软件MS中的Forcite模块对不同尺寸、不同温度以及不同掺杂浓度的硅纳米梁进行分子动力学模拟,模拟时间步长设为1 fs,模拟时间为50 ps.

3.2 模拟结果

本文采用分子动力学方法模拟研究了掺杂浓度分别为30×1020cm−3和7.5×1020cm−3,横截面积S为16A×16A,长度尺寸L从40A到60A(长度尺寸变化间隔∆L=4A)的硅纳米梁在不同温度下的谐振频率.当硅纳米梁的横截面积S为16A×16A,通过对不同长度尺寸的单晶硅纳米梁在不同温度下进行分子动力学模拟,得到单晶硅纳米梁的谐振频率随温度的变化曲线,如图5所示.

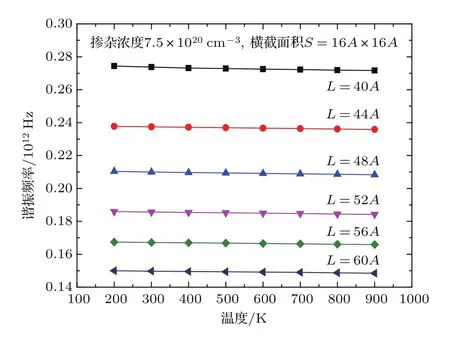
图5 (网刊彩色)不同长度硅梁的谐振频率随温度的变化Fig.5.(color online)The resonance frequency of the silicon nano-beam as a function of the temperature and the length.

由图5可知,当掺杂浓度一定时,横截面积为16A×16A的硅纳米梁的谐振频率随着温度的增大而减小,但减小的趋势并不明显,谐振频率的值十分接近,说明温度对单晶硅纳米梁的谐振频率的影响很小;当温度一定时,硅纳米梁的谐振频率会随着长度尺寸的增加而逐渐较小,并且减小的趋势逐渐变缓,这个结果与文献[15,24]使用分子动力学模拟的硅梁的谐振频率随长度尺寸的变化趋势是一致的.文献[16]通过分子动力学模拟研究了在温度300 K,横截面积为8A×8A,长度尺寸由12A到32A的硅纳米梁的谐振频率,也得到了相同的变化趋势.通过分析长度尺寸与温度对硅纳米梁谐振频率的影响可知∶长度尺寸对硅纳米梁具有较大的影响,即掺杂单晶硅纳米梁的谐振频率与纯单晶硅纳米梁的谐振频率一样具有尺寸效应,温度对硅纳米梁的谐振频率基本无影响.由于硅纳米梁的表面存在许多悬挂键,但随着梁尺寸的增大,梁的体表比不断增大,表面的原子相对于内部原子所占比率不断减小,内部原子的相互作用越来越明显,即硅纳米梁的谐振频率会随着尺寸的变化而变化.其次,硅纳米梁的晶格常数随着温度的增大而增大[25],即硅纳米梁的尺寸随着温度的增大而增大,所以谐振频率随着温度的增大而减小.由此可知,温度并不是影响谐振频率的主要因素,而影响谐振频率的主要因素是单晶硅纳米梁的长度尺寸.

关于掺杂浓度对硅纳米梁谐振频率的影响,以掺杂浓度为7.5×1020cm−3和30×1020cm−3为例,对长度为60A,横截面积为16A×16A的硅纳米梁的谐振频率随温度变化的模拟结果进行分析.

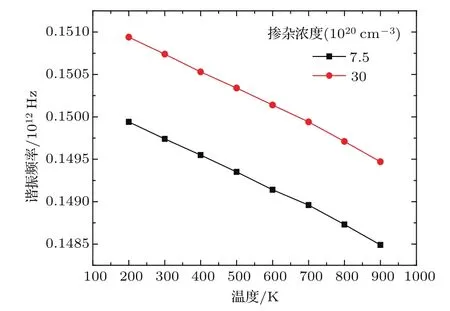
图6 (网刊彩色)不同掺杂浓度的硅纳米梁的谐振频率随温度的变化Fig.6.(color online)The resonance frequency of the silicon nano-beam as a function of the temperature and the doping concentration.

图6所示为不同掺杂浓度的硅纳米梁的谐振频率随温度的变化.当硅纳米梁的尺寸一定时,不同掺杂浓度的硅纳米梁的谐振频率随温度的增大而减小,但从谐振频率的数值看,减小的趋势并不明显;当温度与尺寸一定时,硅纳米梁的谐振频率随着掺杂浓度的增大而增大,同样从谐振频率的数值看,增大的趋势并不明显.由于磷原子替代掺杂在硅晶胞的体对角线四分之一处,而磷原子半径与硅原子半径相差十分微小,所以当硅晶胞中一个硅原子被磷原子替换后,硅晶胞的结构发生微小的变化,并且磷-硅相互作用与其尺寸有关,这都会对分子动力学模拟的硅纳米梁的振动周期有影响,进而影响其谐振频率.当掺杂浓度增大时,磷-硅相互作用数量增加,甚至还存在磷-磷相互作用,所以掺杂浓度会影响谐振频率.

3.3 理论计算模型与分子动力模拟结果的比较

通过对硅纳米梁谐振频率的理论计算与模拟结果的分析,发现半连续模型的计算结果比分子动力学模拟结果稍大,如图7所示,理论计算与模拟的硅纳米梁谐振频率的趋势是一致的.

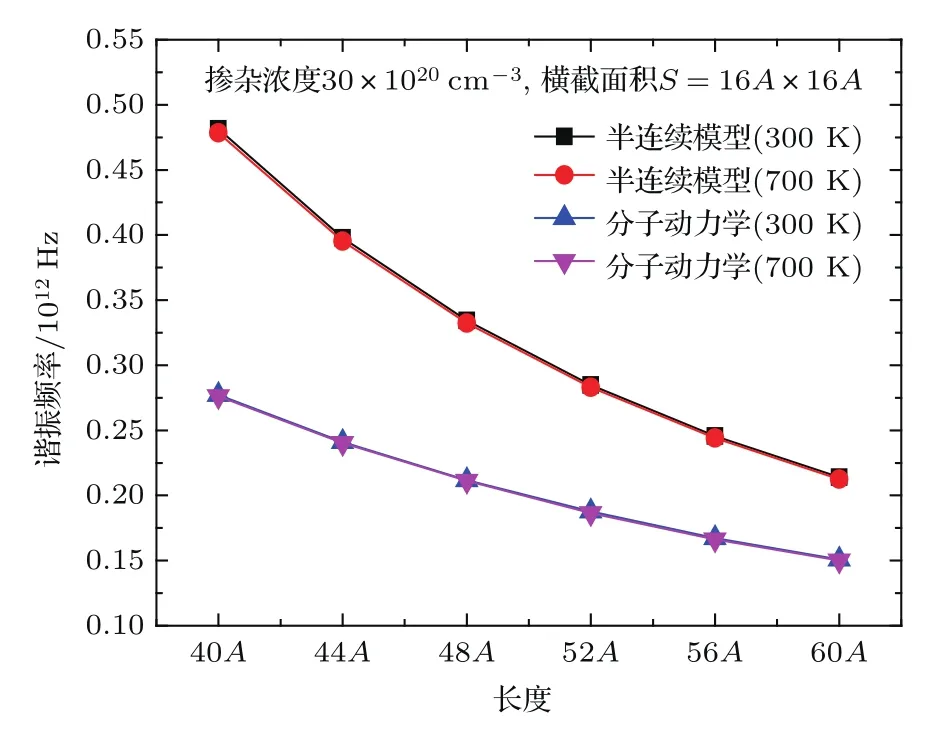
图7 (网刊彩色)半连续模型与分子动力学模拟结果的比较Fig.7.(color online)Comparison of the results of the semi-continuous model and molecular dynamics simulation.

由图7可知,随着硅纳米梁长度尺寸的增大,理论计算结果与模拟结果的差值逐渐减小,当长度为40A,掺杂浓度与温度一定时,硅纳米梁谐振频率的理论计算值与模拟值相差0.22602×1012Hz,当长度为60A时,谐振频率的计算与模拟的差值减小到0.06325×1012Hz.对硅纳米梁谐振频率进行理论计算时比较理想化,只考虑了晶胞内原子之间的相互作用.由于表面效应对硅纳米梁谐振频率具有影响,所以分子动力学模拟相对于理论计算并不是理想化的.当硅梁的尺寸较小时,体表比较小,表面效应相对于内部原子相互作用对硅梁谐振频率的影响更大,当尺寸较大时,体表比相对较大,内部原子相互作用大于表面效应,所以随着梁尺寸的增大,硅纳米梁的计算值与模拟值的差越来越小.从图7可以看出,温度对硅纳米梁的谐振频率基本无影响,而主要影响硅纳米梁谐振频率的是尺寸因素.

4 结 论

本文主要通过半连续模型与分子动力学模拟方法,研究分析了P元素在硅晶胞体对角线四分之一处替代掺杂的硅纳米梁的谐振频率,计算模拟了两端固支硅纳米梁的谐振频率随掺杂浓度、尺寸与温度的变化.结果表明∶当掺杂浓度与温度一定时,硅纳米梁的谐振频率随着长度尺寸的增大而减小,且随着长度尺寸的增大,谐振频率减小的趋势逐渐减小;当硅纳米梁的尺寸一定时,硅纳米梁的谐振频率随着掺杂浓度的增大而增大,但变化趋势并不明显,基本不影响硅纳米梁的谐振频率;当硅纳米梁的尺寸与掺杂浓度一定时,发现掺杂硅纳米梁的谐振频率随着温度的增大而减小,但变化趋势并不明显,温度对硅梁谐振频率基本无影响.由此得出掺杂浓度与温度对硅纳米梁谐振频率的影响很小,而影响单晶硅纳米梁谐振频率的主要因素是尺寸大小,即掺杂硅纳米梁的谐振频率与纯硅纳米梁的谐振频率一样,具有尺寸效应.本文研究结果对未来纳米材料的研究与应用具有一定的参考价值.

[1]Huang X M H,Ekinci K L,Yang Y T,Zorman C A,Mehregany M,Roukes M L 2002 Appl.Phys.Lett.81 2253

[2]Yang Y T,Callegari C,Feng X L,Ekinci K L,Roukes M L 2006 Nano Lett.6 583

[3]Yang Y T,Callegari C,Feng X L,Roukes M L 2011 Nano Lett.11 1753

[4]Bargatin I,Myers E B,Aldridge J S,Marcoux C,Brianceau P,Duraffourg L 2012 Nano Lett.12 1269

[5]Arkan E F,Sacchetto D,Yildiz I 2011 J.Micromech.Microeng.21 125018

[6]Koumela A,Hentz S,Mercier D,Ollier E,Feng P X,Purcell S T 2013 Nat.Nanotech.24 435203

[7]Li X X,Ono T,Wang Y,Esashi M 2003 Appl.Phys.Lett.83 3081

[8]Sun C T,Zhang H 2003 J.Appl.Phys.93 1212

[9]Bao F,Yu H,Lu Q,Huang Q 2007 Chin.J.Semi.28 1979

[10]Lu Q R,Bao F,Yu H,Huang Q A 2008 Chin.J.Sens.Actuat.21 469(in Chinese)[陆清茹,鲍芳,于虹,黄庆安2008传感技术学报21 469]

[11]Wang J,Huang Q A,Yu H 2008 Appl.Surf.Sci.255 2449

[12]Lü H L,Wang J 2015 Acta Phys.Sin.64 236103(in Chinese)[吕焕玲,王静 2015物理学报 64 236103]

[13]Gong B,Chen Q,Wang D 2012 Mater.Lett.67 165

[14]Cao G B,Chen Y F,Jiao J W,Wang Y L 2007 Mech.Res.Commun.34 503

[15]Pishkenari H N,Afsharmanesh B,Tajaddodianfarf2016 Int.J.Eng.Sci.100 8

[16]Lü H L,Wang J 2016 J.Xinjiang Univ.33 421(in Chinese)[吕焕玲,王静 2016新疆大学学报 33 421]

[17]Rücker H,Methfessel M 1995 Phys.Rev.B 52 11059

[18]Wang J 2012 The Sixth Asia-Pacific Conference on Transducers and Micro/Nano Technologies Nanjing,China,July 8–11,2012 ac12000109

[19]Krivtsov A M,Morozovv Nf2002 Phys.Solid State 44 2260

[20]Xu Y,Zhang L C,Yu T X 1987 Int.J.Mech.Sci.29 425

[21]Wang J,Huang Q A,Yu H 2008 J.Phys.D:Appl.Phys.41 165406

[22]Park S H,Kim J S,Park J H,Lee J S,Choi Y K,Kwon O M 2005 Thin Sol.Films 492 285

[23]Li Y N,Zhao J,Guo T 2008 J.Tianjin Univ.41 7(in Chinese)[李艳宁,赵景,郭彤 2008天津大学学报 41 7]

[24]Pishkenari H N,Afsharmanesh B,Akbari E 2015 Curr.Appl.Phys.15 1389

[25]Tang Z,Alueu N R 2006 Phys.Rev.B 74 235441

PACS∶61.72.uf,62.25.—g,81.40.JjDOI∶10.7498/aps.66.106103

*Project supported by the National Natural Science Foundation of China(Grant No.11064014).

†Corresponding author.E-mail:wjxju@163.com

Study on resonance frequency of doping silicon nano-beam by theoretical model and molecular dynamics simulation∗

Ma Xia Wang Jing†
(College of Physical Science and Technology,Xinjiang University,Urumqi 830046,China)

23 December 2016;revised manuscript

28 February 2017)

With the rapid development of nanoelectromechanical system technologies,silicon nanostructures have attracted considerable attention for the remarkable mechanical properties.A number of studies have been made on the mechanical properties through theoretical analysis,atomistic or molecular dynamics and experiments.In this paper,the resonance frequency of the doping silicon nano-beam is investigated by a theoretical model based the semi-continuum approach to achieve the goalof accurately capturing the atomistic physics and retaining the efficiency of continuum model.The temperature dependence of the resonance frequency of the nanostructure is important for application design,which is considered by the Keating anharmonic modelused to describe the strain energy atfinite temperature.The resonance frequencies are also simulated by the molecular dynamics at different temperatures.The studies indicate that the resonance frequency of the P doped silicon nano-beam is influenced by the size,the doping concentration and the temperature.The results show that the resonant frequency decreases with the increase of the length of the beam,and increases with the increase of the doping concentration of the silicon nano-beam.The resonant frequency of silicon nano-beam decreases with the increase of temperature,but the changes of the resonant frequency is not obvious.The doping concentration has a little effect on the resonance frequency of the silicon nano-beam.The conclusion can be drawn that neither the effect of doping concentration nor the effect of temperature on resonant frequency of the silicon nano-beam is obvious,the size is a major factor influencing the resonance frequency of the silicon nano-beam.

∶silicon nano-beam,resonance frequency,doping,temperature

∗国家自然科学基金(批准号:11064014)资助的课题.

†通信作者.E-mail:wjxju@163.com

©2017中国物理学会Chinese Physical Society