代表性社区集发现

武晓伟， 赵琼

(复旦大学 软件学院，上海 200433)



代表性社区集发现

武晓伟， 赵琼

(复旦大学 软件学院，上海 200433)

随着计算机的普及和互联网的快速发展，社交网络的使用也越来越普遍。信息在社交网络上呈爆炸式传播，越来越多的热门事件、网络红人在互联网上出现，同时这些事件或者人物会通过联系聚集为不同的群体或者社区，从而产生巨大的影响力。因此，互联网、生物学、经济学等各类学科中的社区问题逐渐成了研究热点，对社区进行研究发展成为了一个新兴的方向。然而，进行社区发现后所得到的数据量仍是庞大的，因此，社区发现相关工作完成之后，对社区发现的结果进行优化和进一步处理的相关研究也逐渐兴起并且受到重视。为了达到以上目的，使社区及其相关理论能够应用到实际中，实现从理论到应用的转型，提出了代表性社区集发现算法。

社区发现； 代表性社区集； 邻居节点覆盖程度； Jaccard距离

0 引言

互联网的快速发展让信息获取更为便捷和高效，铁路网、城市公共交通网的不断扩建让居民出行更加方便，基因图学的研究更为人体遗传和人体构造等揭开了神秘面纱，这种种的研究与进步都与复杂网络息息相关。在现实生活中，微博、微信朋友圈、豆瓣、知乎、facebook、推特、电力网、生物学、基因图谱、文献引用、神经网络、演员关系等各类学科以及与个人生活紧密相关的应用及事物都以复杂网络为基础。而在复杂网络的研究中，社区发现的相关研究是早期便引起关注、得到重视的一个方向。

随着社区发现的深入研究，对于社区质量、社区多样性等方面的要求越来越高。在社区中，高质量的具有代表性的社区往往具有极为重要的现实意义。社区发现完成后，对社区的质量、代表性等方面的研究，可以实现不同领域的诉求，是社交网络、互联网、生物网络等多个领域的热门，更是社区研究的必然发展方向之一。

1 研究现状

1.1 相关概念

复杂网络可以认为是对一个复杂系统的抽象和描述方式，是呈现出高复杂度的网络。我们可以将复杂网络理解为一个通过连接来标识两者之间是否具有联系的一些个体的集合。复杂网络虽然没有明确的定义，但是我国著名科学家钱学森在上世纪80年代给出的复杂网络的定义是认可度较高的。他给出的复杂网络较为严格的定义是：具有自组织、自相似、吸引子、小世界、无标度中的一部分性质或者全部性质的网络称为复杂网络。

社区到目前为止并没有确定的定义，目前认可度较高的是由Newman和Girvan在2004年提出的社区定义[1]，认为社区是一个子图，在这个子图内，节点与节点之间的联系较为紧密，而该社区与其他社区之间的联系较为稀疏。社区的存在能够让我们了解到生物网络中新陈代谢的规律，社交网络中用户间的关系，论文网络中互相引用的关系。更重要的是，通过对社区的研究，我们可以发现一些从单独个体不能发现的一些特征和性质，比如个体之间的内在联系等[2]。

1.2 研究水平及发展趋势

随着各类社区发现算法的不断提出，国内外对于社区发现的研究逐渐趋于成熟。在现有社区发现算法中，根据所处理的数据是图、构造树，图是有向图或者无向图，是否为加权图等，子图之间是否有重叠，又或者从图的整体考虑或者从某一主要部分考虑等等方式，将社区发现的算法分为不同类别。在不同分类类别中，有一些较为经典的，具有代表性的算法。

针对于如何提高社区发现的质量，使其具有现实意义和应用价值，各类学者也做了大量的研究。研究的通用做法一般是在社区发现的过程中，加入特定的需要考虑的因素，通过该因素使社区发现算法具有较好的运行效果，应用在现实场景中。如为了使挖掘出的社区具有分值且该分值代表社区可获得的效应，Petko等人提出了在加权图中，将最弱连接作为打分基准的思想[3]，该算法可应用于对NBA球对进行打分，以找出具有最佳配合效果的选手。Chekuri采用了数学方法解决分组问题[4]。Tianbao Yang等人在提取社区时，将连接关系与社区内容结合，同时考虑两者，考虑节点之间的连接关系如被引用、被指向等是具有意义的，可以代表与社区相关的属性等，从而来提高社区发现的准确度，他们认为在复杂网络中，连接关系与内容都是不可或缺的一部分，否则会造成社区发现性能不佳[5]。

在不同社区发现过程中，结合其领域特征以及现实意义，加入不同的考虑因素，会使得该领域范围内挖掘出的社区质量较高，符合实际要求，这是现有社区发现算法中，提高社区质量的常见做法。

2 问题定义

2.1 应用场景

在以往的研究中，我们意识到在进行社区发现研究的过程中，虽然将复杂网络中连接紧密或者具有某方面共同性质的节点划分在同一个社区，但是即使进行划分之后，所提取出的社区数目也是较多的。因此即使进行了社区发现，在一些情况下这些大量的社区也不利于现实分析和使用。例如，在Amazon的一个物品合作采购的复杂网络中，其节点数量为334,863，边的数量为925,872，通过社区发现算法获得的社区数目高达75,149个[6]。因此如何从大量的社区中，提取出代表性的社区，是一个亟待解决的问题，它对于用户进行决策，节省时间、人力、物力资源等具有非常重要的意义和作用，这也是本文进行研究的主要动机。

2.2 代表性社区集定义及性质

以上问题的解决过程，可以总结为从大量的社区中，如何提取出代表性社区集，以帮助我们解决现实生活中所碰到的困难的过程，是具有一定的现实应用场景的和现实意义的。本文所进行的关于代表性社区集发现的相关研究，是解决该类现实问题的一个途径之一，具有重要的意义和作用。

代表性社区集：本文认为，代表性社区集是指在社区发现这一步骤完成之后，从若干个数量较大社区群中，选取出一个由k个社区组成的社区集合S，该集合S能够最大程度的涵盖整个社区群中不同类型社区的性质，在一定程度上对该社区群的其他社区具有较大的影响力，是可以代表该社区群的一类社区集合。称该集合S为代表性社区集。可以看出，代表性社区集发现的过程是最优子集选取问题，可以将其归约为NP-问题[7]。

在研究复杂网络的社区分布情况时，为了将无数社区中的代表性社区集提取出来，基于以上的定义，本文认为代表性社区集应该具有如下的性质。

代表性社区集的性质：

1) 若一个社区被选入代表性社区集，那该社区自身需要具有较高的质量。

2) 相对于其他未被选入的社区，代表性社区集作为一个整体与其邻居节点的连接应该是更紧密的、其邻居节点的数目应是更多的，或者其邻居节点在整个社区群中是更为重要的。我们称该性质为代表性社区集的邻居节点覆盖程度，是代表性社区集的一个属性。即代表性社区集的邻居节点覆盖程度较高，该社区对其周围社区的影响力较大。

3) 代表性社区集应具有能够体现整个社区群中不同社区类型的性质，能代表大多数节点。对于整个社区群来说，其包含的社区数目众多，类型也各有不同，不同的社区可能具有不同的含义或者特性，因此只有代表性社区集在最大程度上包含这些不同类型特性的社区，才具有普遍代表性，即代表性社区应具有代表大多数节点或代表不同类型节点的特性。

我们可以将以上性质认为是代表性社区集必备的性质。具有这类性质的社区在所有的社区中具有重要的意义，通过对该类代表性社区集的研究，可以对整个社区群的研究提供一定的支持。

2.3 代表性社区集发现

给定一个图或者是一个社交网络，用G=(V,E)来表示，V代表该图中所有的点的集合，E代表该图中所有边的集合。定义该图中的所有社区为C=(C1,C2,…,Cl),Ci⊆V,i≥1，这里的社区可以是重叠或非重叠社区。设代表性社区集某一性质的评分函数为f(S)，则寻找代表性社区集的过程即是找到arg maxf(S)的值，通过寻找该值，最终获得整个社区群的一个子集{Ci:i∈S⊆{1,2,…,l}}，其中|S|=k。

本文希望通过提出一个社区的评分函数来衡量和评估该社区是否具有代表性，是否将其选取到代表性社区集集合中，同时通过对应的算法实现，解决在所有的社区中，寻找到社区个数为的代表性社区集的问题。

4 基于Jaccard距离的代表性社区集发现算法及改进

衡量一个代表性社区集是否具有代表性的一个方面是，该代表性社区集是否能够最大程度的涵盖整个集合即整个社区群中不同类型的社区。因此，在本章我们综合考虑一个社区的自身质量及其是否能够包含不同类型社区的特性这两个因素，提出了两个基于Jaccard距离的代表性社区集挖掘算法。如果通过算法所获得的代表性社区集能够代表整个社区群中不同的社区类型，则该社区集才具有普遍代表性。因此本章除了考虑一个社区的自身质量外，还引入了Jaccard距离来衡量被选入的社区集合是否具有普遍代表性。

综合考虑一个社区自身质量以及该社区是否能够普遍代表其他节点，首先，假定最终得到的代表性社区集为{C:C1,C2,C3,…,Ck}，其中k≥1且为正整数。定义α为参数，其取值范围为0≤α≤1，N(Ci)是社区Ci所有的邻居节点，即N(Ci)={u∈V:∃v∈Ci,(u,v)∈E}。N(Ci)∩N(Ci)与N(Ci)∪N(Ci)代表两个社区Ci与Cj邻居节点的交集与并集。E(Ci)是指Ci中节点之间边的条数，|Ci|是Ci中节点的个数。q(Ci)代表该社区的质量。g(Si,j)代表对是否选取Ci与Cj两个集合的评分函数，则基于Jaccard距离的代表性社区集评分函数g(Si,j)如下定义为式(1)、(2)。

(1)

(2)

对于基于Jaccard距离的代表性社区集评分函数，初始时需要一次性选择两个社区，其初始值如式(3)。

(3)

我们可以知道，Jaccard距离满足三角不等式，即对于任意的三个集合，i,j,p∈S，任意两个社区的邻居节点组成的集合N(Ci)与N(Cj)之间的Jaccard相似度为D(i,j)，则为式(4)。

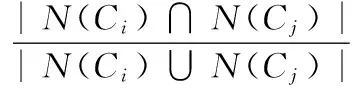
(4)

首先，根据Jaccard距离满足三角不等式，有如下关系：

D(i,j)+D(j,p)>D(i,p)

则对于评分函数g(Si,j)，有以下结论成立：

g(Si,j)+g(Sj,p)=

(q(Ci)+2q(Cj)+q(Cp))+

(q(Ci)+2q(Cj)+q(Cp))+α(D(i,j)+D(j,p))>(q(Ci)+q(Cp))+αD(i,p)=g(Si,p)⟹g(Si,j)+g(Sj,p)>g(Si,p)

基于Jaccard距离的评分函数满足三角不等式，因此我们对寻找最大距离的贪心算法做一些变形，将其中的两个点之间边的权重转化为两个集合之间的质量与Jaccard距离之和即g(Si,j)。利用离散p-扩散问题的相关概念，即如果其满足三角不等式，我们可以通过使用寻找最大距离的贪心算法来解决该问题[8]，评分函数(2)同理可证。

5 基于邻居节点覆盖情况的代表性社区集发现算法

在社会学中，核心-边缘结构模型是一种较为经典的理论模型，该模型由J. R. Friedmann提出。在该理论中，核心与边缘之间存在着不平等的发展关系。简单来说，核心部分具有统治地位，边缘在发展上或者其他方面依赖于核心。在计算机科学的研究中，Jure Leskovec提出了AGM模型(Community-affiliation Graph Model)[9]，同时他阐释了在一个复杂网络中，核心-边缘结构是存在并且具有意义的。在复杂网络结构中有一部分是核心，这些核心部分具有和复杂网络其他部分共有的特性，而除此之外其余边缘的部分可以看作是“尾巴”，核心部分的邻居节点覆盖情况是决定该部分是否是核心的重要因素。因此在本文中，我们将核心-边缘理论引入到算法中，利用该社会学概念，通过一个部分的邻居节点覆盖程度来衡量一个部分是否为核心部分，若邻居节点覆盖率较多或者覆盖程度较高，那我们可以认为其能够代表其他部分的特性，同时具有较强的影响力。

根据以上的性质，在一个社区群中，我们综合考虑其中某一个社区自身的质量以及该社区的邻居节点覆盖情况，将这两个因素作为挖掘代表性社区集的关键因素，提出如下基于邻居节点覆盖情况的代表性社区集发现算法。

基于邻居节点覆盖率的代表性社区集发现算法及其改进

我们综合考虑一个社区的自身质量以及其邻居节点覆盖率，首先，假定最终得到的代表性社区集为{Ci:i∈S⊆{1,2,…,l}}，其中S|=k，i≥1且为正整数。定义α为参数，其取值范围为0≤α≤1，N(Ci)是社区Ci所有的邻居节点，即N(Ci)={u∈V:∃v∈Ci,(u,v)∈E}，E(Ci)是指Ci中节点之间边的条数，|Ci|是Ci中节点的个数。q(Ci)代表该社区的质量，我们这里将其定义为Ci内部平均边的条数。则基于邻居节点覆盖率的评分函数定义如式(5)、(6)。

(5)

(6)

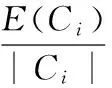
其中，该函数的初始条件如式(7)。

f(S1)=q(C1)+αN(C1)

(7)

对于该评分函数(1)，我们可以证明其属于次模态函数，证明过程如下。对于任意的集合S与T，其中S⊆T，且i∉T，有以下证明过程成立：

(∪j∈SN(Cj))|≥q(Ci)+α|N(Ci)(∪j∈TN(Cj))|=f(T∪{i})-f(T)⟹f(S∪{i})-f(S)≥f(T∪{i})-f(T)

因此，该评分函数符合边际递减效应，且该函数是非负函数，因此属于次模态函数。因为q(Ci)与∪i∈SN(Ci)的数量级并不相同，所以我们在进行具体计算时会将其分别进行线性归一化，将其转化为无量纲表达式，利用线性归一化后的值来进行计算。因为线性归一化并不会改变函数的性质，因此归一化后，该函数仍然符合次模态函数的次模性。同理可证明评分函数(2)。

6 总结

论文首先介绍了社区、社区发现等基础理论，综述了前人在社区及社区发现方面的相关研究，总结、梳理并且分析了常见的社区发现方法，阐明了社区发现在现实生活中的实际应用以及其重要意义。但是随着研究的深入，提出了社区发现目前在应用中的不足之处，针对该问题提出了研究代表性社区集发现的必要性和意义。

本文通过对社区进行深入的研究，提出了代表性社区集的定义，以及代表性社区所需具有的性质，之后对代表性社区集发现进行建模。通过数学领域的次模态函数以及最大p-扩散问题模型的理论支撑，本文提出了两类代表性社区发现算法：基于Jaccard距离的代表性社区集发现算法以及基于邻居节点覆盖情况的代表性社区集发现算法。在提出核心算法的同时，我们证明了这两类代表性社区集发现算法具有数学理论支撑，从理论上来说具有可行性。

[1] Newman M E, M Girvan. Finding and evaluating community structure in networks[J]. Physical Review E (Statistical Nonlinear & Soft Matter Physics), 2004, 69(2): 026113-026113.

[2] Mucha, P.J., et al., Community structure in time-dependent, multiscale and multiplex networks[J]. Science, 2010, 328: 876-878.

[3] Bogdanov, P., et al., As Strong as the Weakest Link:Mining Diverse Cliques in Weighted Graphs[M]. Berlin Heidelberg Springer, 2013: 525-540.

[4] Chekuri, C., G. Even and G. Kortsarz, A greedy approximation algorithm for the group Steiner problem[J]. Discrete Applied Mathematics, 2006, 154(1): 15-34.

[5] Yang, T., et al., Combining Link and Content for Community Detection[M]. New York: Springer, 2014: 190-201.

[6] Held, P. and R. Online Community Detection by Using Nearest Hubs[J]. arXivpreprint arxrXiv: 2016, 1601.06527.

[7] 陈彬, 洪家荣，王亚东. 最优特征子集选择问题[J]. 计算机学报, 1997(2): 133-138.

[8] Hassin R S. Rubinstein, A Tamir. Approximation algorithms for maximum dispersion[J]. Operations Research Letters, 1997, 21(3): 133-137.

[9] Yang J, Leskovec J. Overlapping Communities Explain Core-Periphery Organization of Networks[J]. Proceedings of the IEEE, 2014, 102(12): 1892-1902.

Finding Representative Communities

Wu Xiaowei,Zhao Qiong

(Fudan University Software School， Shanghai 200433, China)

With the popularization of computer and rapid development of the Internet, the use of social networks is becoming more and more popular. Information in social networks is spreading explosively, increasingly popular events and web celebrities appear on the Internet. These events or people gather into different groups or communities through different connections, and produce enormous leverage. Therefore, communities of the Internet, biology, economics and other disciplines have become a hot topic of research gradually. Researches on the community have become a burgeoning area. The research on community belongs to complex network research area, it has irreplaceable significance in computer science, biology and other disciplines. However, the data size is still huge after community detection. Therefore, once the community detection is completed, how to optimize and what we can do to process the result further are aspects that are gradually on the rise and have been highly attached. In order to achieve the purpose, and to make the community and related theory applied to practice, this paper proposes the representative communities mining algorithm.

Community detection; Representative communities; Neighbor coverage; Jaccard distance

武晓伟(1992-)，男，硕士研究生，研究方向：电子商务与电子政务。 赵琼(1991-)，女，硕士研究生，研究方向：电子商务与电子政务。

1007-757X(2017)07-0073-03

TG409

A

2017.03.01)