微流控低通二阶滤波器的特性研究

孙开文，梁忠诚，赵 瑞，孔梅梅，吴雯婷，张 曼



微流控低通二阶滤波器的特性研究

孙开文，梁忠诚，赵 瑞，孔梅梅，吴雯婷，张 曼

（南京邮电大学 微流控光学研究中心，江苏 南京 210023）

微流控滤波器对于交变流路选频，获得特定频率或稳定的交流流体输出具有重要作用。利用微流控等效电路理论设计了一个π型微流控二阶低通滤波器。该微流控滤波器由三段矩形微流道与两个微腔组成，通过改变微流道的深宽比和微腔的半径，分析了该滤波器的带宽特性。结果表明，随着微通道的深宽比减小，滤波器的截止频率按指数衰减；截止频率随着微腔半径的增加也呈指数下降。验证了微流控等效理论分析结果与流路仿真结果一致。

微流控技术；滤波器；等效电路理论；深宽比；截止频率；微腔

目前，微流控系统已经有很多成熟的应用[1-3]，但是在设计和研究时流路的输入输出通常限于相对稳定的层流[4]。近年来，通过使用交流的输入获得规则交流输出已经成为研究热点[5-7]。这是微流体系统研究的进步，类似于电子学从直流到交流的发展，在未来，交变压力流体作为驱动源来驱动整个微流体系统，基于交变流路的微流控系统将成为研究的趋势。在交变微流控系统中微流控滤波器起着稳压、稳流、选频等作用，所以研究微流控滤波器具有重要意义。

通常采用微流体等效电路理论对微流控系统进行理论分析。其理论体系的成立必须满足三个条件：流体的状态是层流，流体的粘性不可忽略以及流体不可压缩。流体方程可以类比于电路方程，电路的定律在流体运动中具有等价性[6-9]。流体流量等效于电流，流体压力差Δ等效于电压差Δ，流路中感性储能元件流感等效于电感e，流路中容性储能元件流容等效于电容e，流阻等于Δ与流体流量之比。电路分析能够快速预测微通道中流体的运动状态，比如直线微通道的稳态压降、流速和液压阻力等[10]，并且有利于在制造器件之前进行复杂的微流体网络设计。微流体的等效电路理论目前已被广泛地应用于很多领域，如：在微流体逻辑门和定时器[12]、微流体振荡器[13]以及流体混合器[14]等。因此，类比于电子学中的这种方法，结合其理论特性中的优势，为设计和制造微流体器件找到了一种新的渠道。

本文设计一个二阶低通微流体滤波器，以支持在未来交流流体微流控系统的设计。这种微流体滤波器配备有三个微流道和两个弹性微腔。通过将软件仿真结果与理论值进行比较，验证了文中提出的模型等效电路的正确性，并获得交流流体输出。此外，还研究了结构尺寸对滤波器特性的影响。根据结论，可以有效调整微系统的结构以满足不同流路性能指标需求。

1 滤波器结构

本文设计的微流控二阶低通滤波器包含三段矩形微流道与两个微腔。在该结构中，两个弹性微腔在滤波中起着主要作用。此外，可以通过改变微腔的半径、数量以及矩形微流道的高度和宽度等结构参数，以实现不同的频率筛选，从而可以根据不同的需要调整系统结构。首先，本文设计了滤波器的结构，如图1所示。微流体滤波器中的所有组件在三层聚二甲基硅氧烷（PDMS）基底中制造如图1（a）。微流道和微腔室在同一层中，中间层为弹性膜，由于中间层很薄，最上层用于保护，有两个孔，其中间的可变形膜可以偏转到空腔或相对侧。

图1(b)为微流控二阶低通滤波器的结构模型示意图，其更加直观地表现出了各主要结构参数，包括微流道、微腔和弹性膜三部分。其入口由交变压流体驱动。在流道入口、第一个微腔出口、第二个微腔出口分别设置三个压力1，2和3。大气中的气压设为0，模型中压力降分别为Δ1=1–0，Δ2=2–0，Δ3=3–0分别对应于电压1，2和3。微流道的宽度为，高为，长分别为1，2，3，微腔的半径分别为1，2。弹性膜覆盖在微腔上，高度为1，半径与相应的腔半径一致。三个通道的液压阻力和流感分别对应于1、1，2、2和3、3。弹性微腔对应于流容1、2。令1=1+jL1，2=2+jL2，L=3+jL3，通过微流控等效电路理论，得到的模型等效电路如图1（c）所示。其中由于弹性膜与大气接触，对应于电路中的接地。可以看出该电路是一个带负载的π型滤波电路。

(a)

(b)

(c)

2 理论分析

为了设计出简易高效的微流控系统，首先需要对微流控滤波器等效电路进行理论分析，电路中具有三个基本元件：电阻、电容及电感，分别用于推导出流阻、流容及流感的公式。其中具有宽度，高度为和长度的长方形横截面的流阻[14]：

式中：是流道中液体的动力粘度；是矩形流道的深宽比。流体系统的储能元件显示出薄膜的形变与所受的压力有关。圆形膜流体的流容[15]公式为

（2）

式中：是膜的杨氏模量；1是膜厚度；是泊松比；是膜的半径。对于横截面为，长度为的矩形流道，流体流感[16]公式为：

式中：为液体的密度。

图2所示为图1(c)电路的变换形式，其中将L看作负载，，。

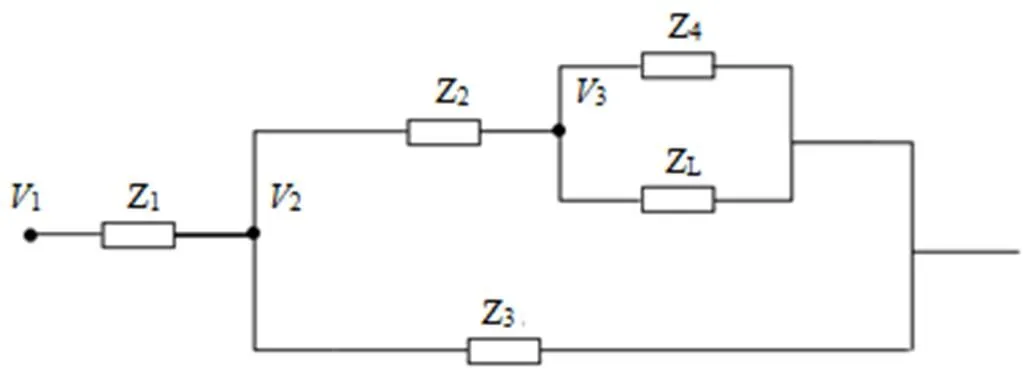
图2 变形等效电路

对于电路图2，其中1=1+jL1，2=2+jL2，，，3=3+jL3，其传递函数为：

当1=2=3，1=2=3，1=2，将负载、电阻等参数代入（4）式，可得传递函数为：

（5）

式中：j表示虚数单位；是角频率。

其幅频特性函数为：

3 结果及讨论

对于上述所设计的结构，采用仿真方法建模进行研究。实验中使用的液体为常温下的水溶液，其密度和粘度必须分别保持在103kg/m3和10–3Pa·s。杨氏弹性模量和泊松比分别为750 kPa和0.45，以确保流体的运动状态为层流。结构中三段微流道的长度相同，两个微腔的尺寸一致。典型模型的尺寸分别为：流道的长=2 mm，宽度=0.1 mm，深度=0.1 mm，微腔的半径=0.5 mm，弹性膜的厚度1=0.03 mm。那么，通过公式（1）、（2）、（3）计算得=2.4×1011Pa·s/m3，=7.7289×10–12m3/Pa，=2×108Pa·m2/m3，代入公式（6）可得其幅频特性，令等式（6）的分母为零，可求得其截止频率c=32.7245 Hz。根据给定参数进行COMSOL仿真，得到的仿真曲线如图3。由图3可知，该系统是具有截止频率的低通滤波器特性，其中理论幅值比实际的仿真幅值大一点，理论截止频率小于仿真值，仿真截止频率c由图3可知为33.4 Hz，其误差为2.064%。分析其产生误差的原因是：微腔存在一定的流阻，其值较小，在等效电路理论计算中没有考虑。在实际操作中，存在的误差比较小，可以忽略，因此理论推导结果与实际的仿真结果相互一致得到验证。

图3 滤波器动态响应频率曲线及截止频率

图4给出了100 Hz时滤波效率的数值图。显然，过滤器越多，流体越稳定。在二阶滤波器之后，频率为100 Hz的输入基本被完全滤掉。

图4 滤波器的效果图

为了更好地满足设计需要，通过改变微腔的半径大小，研究该滤波器的带宽特性。经过仿真模拟，得出结论：随着微腔半径的增加，截止频率呈现指数减小，如图5。图5是截止频率随微腔半径的变化。其中实线是理论值，点表示的是仿真值，仿真点的拟合曲线为1=/(1+ex)，其中为 5.006 79×105，为20.4。可以看出图5中理论与仿真随着半径的增加，仿真截止频率的偏差将上升。这是由于随着半径的增加，微流腔的流阻将增大，对结果的影响也将增大。这与图3中表现的理论与仿真存在差异一致，两者的结果得到相互验证。

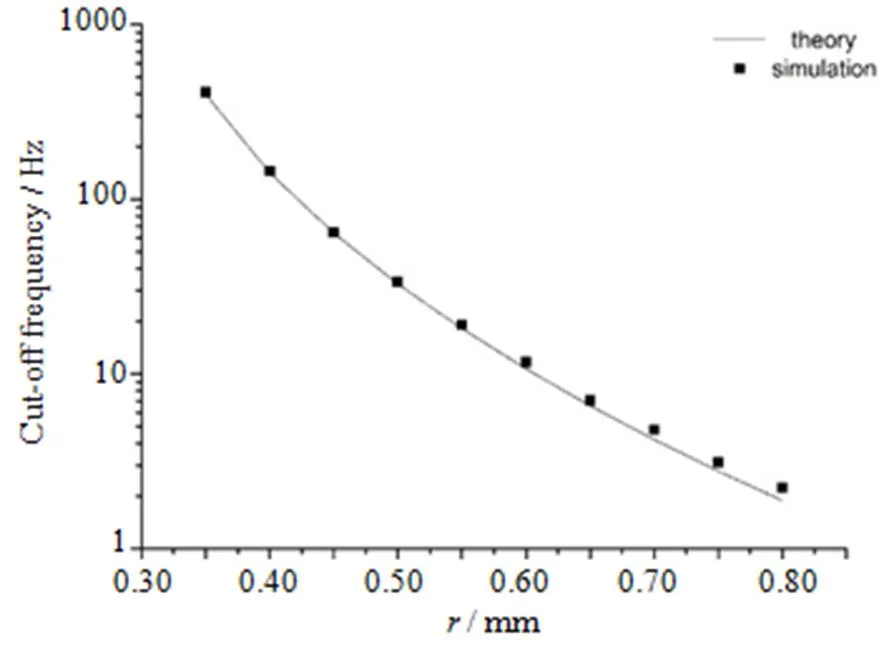
图5 截止频率随微腔半径r的变化

分析微流道的深宽比对该滤波器特性的影响，如图6。结果表明：随着的减小，即随1/值的增加，截止频率呈现指数减小。其中实线是理论值，点表示的是仿真值，仿真值点的拟合曲线为2=1/(1+ex)。其中1为1.376 67×105，为1.7，为1.3384×103。现在需要设计截止频率为c1=50Hz的低通滤波器，根据图6可知，需要深宽比的倒数1/为0.667。将数据代入（6）式，计算出理论截止频率为c2=48.7 Hz，其与理论值误差为2.6%。其对实际设计具有很好的指导意义。

图6 截止频率随微流道深宽比的变化

4 结论

本文设计了一种微流体二阶低通滤波器，主要利用微通道和微腔室来实现滤波的功能，可以对输入的交流流体的频率进行选频，使较低频率通过，过滤掉高频的输入。该微流控滤波器结构比较简单，可以与其他模块集成完成比较复杂的微流控系统。仿真时对于模型的输入输出与利用微流控等效电路理论分析的结果一致。研究结果表明：通过增大深宽比或增加微腔的半径，可以减小截止频率；反之，带宽变宽。

[1] ABDULLA Y H, BALDOCK S J, BARBER R W, et al. Optimisation and analysis of microreactor designs for microfluidic gradient generation using a purpose built optical detection system for entire chip imaging [J]. Lab Chip, 2009, 9(13): 1882-1889.

[2] DERTINGER S K W, CHIU D T, JEON N L, et al. Generation of gradients having complex shapes using microfluidic networks [J]. Anal Chem, 2001, 73(6): 1240-1246.

[3] GÓMEZ-SJÖBERG R, LEYRAT A A, PIRONE D M, et al. Versatile, fully automated, microfluidic cell culture system [J]. Anal Chem, 2007, 79(22): 8557-8563.

[4] THORSEN T, MAERKL S J, QUAKE S R. Microfluidic large-scale integration [J]. Science, 2002, 298(5593): 580-584.

[5] OLSSON A, STEMME G, STEMME E. A numerical design study of the valveless diffuser pump using a lumped-mass model [J]. J Micromech Microeng, 1999, 9(1): 34.

[6] BRASK A, SNAKENBORG D, KUTTER J P, et al. AC electroosmotic pump with bubble-free palladium electrodes and rectifying polymer membrane valves [J]. Lab Chip, 2005, 6(2): 280.

[7] LESLIE D C, EASLEY C J, SEKER E, et al. Frequency-specific flow control in microfluidic circuits with passive elastomeric features [J]. Nat Phys, 2009, 5(3): 231-235.

[8] LIN K, HOLBERT K E. Applying the equivalent pi circuit to the modeling of hydraulic pressurized lines [J]. Math Comput Simulat, 2009, 79(7): 2064-2075.

[9] OH K W, LEE K, AHN B, et al. Design of pressure-driven microfluidic networks using electric circuit analogy [J]. Lab Chip, 2012, 12(3): 515.

[10] HSU Y C, LE N B. Equivalent electrical network for performance characterization of piezoelectric peristaltic micropump [J]. Microfluid Nanofluid, 2009, 7(2): 237-248.

[11] 梁忠诚, 徐宁, 涂兴华, 等. 新颖的微流控光学变焦透镜阵列集成器件 [J]. 光电工程, 2008(9): 32-35.

[12] DEMORI M, FERRARI V, POESIO P, et al. A microfluidic capacitance sensor for fluid discrimination and characterization [J]. Sens Actuators A-Phys, 2011, 172(1): 212-219.

[13] TOEPKE M W, ABHYANKAR V V, BEEBE D J. Microfluidic logic gates and timers [J]. Lab Chip, 2007, 7(11): 1449-1453.

[14] KIM S J, YOKOKAWA R, LESHERPEREZ S C, et al. Constant flow-driven microfluidic oscillator for different duty cycles [J]. Anal Chem, 2012, 84(2): 1152-1156.

[15] BAHRAMI M, YOVANOVICH M M, CULHAM J R. A novel solution for pressure drop in singly connected microchannels of arbitrary cross-section [J]. Int J Heat Mass Transfer, 2007, 50(13/14): 2492-2502.

[16] BOUROUINA T, GRANDCHAMP J P. Modeling micropumps with electrical equivalent networks [J]. J Micromech Microeng, 1999, 6(4): 398.

（编辑：陈丰）

Analysis of microflow control low-pass second-order filter

SUN Kaiwen, LIANG Zhongcheng, ZHAO Rui, KONG Meimei, WU Wenting, ZHANG Man

(Microfluidics Optical Research Center, Nanjing University of Posts and Telecommunications, Nanjing 210023, China)

Microfluidic filter plays an important role in frequency selection of alternating flow path, obtaining specific frequency or stable AC fluid output. Based on the theory of microfluidic equivalent circuit, a π-type microfluidic second - order low - pass filter was designed. The microfluidic filter consists of three sections of rectangular microchannel and two micro-cavities. The bandwidth characteristics of the filter were analyzed by changing the aspect ratio of the microchannel and the radius of the micro-cavity. The results show that the cut-off frequency of the filter decreases exponentially with the aspect ratio of the microchannel. The cut-off frequency decreases exponentially with the increase of the micro-cavity radius. It was verified that the results of microfluidic equivalent theoretical analysis were consistent with the simulation results of flow path.

microfluidic technology; filter; equivalent circuit theory; aspect ratio; cut-off frequency; micro-cavity

10.14106/j.cnki.1001-2028.2017.08.014

TN713；O357

A

1001-2028（2017）08-0080-04

2017-05-11

梁忠诚

国家自然科学基金资助项目（No. 60878037）

梁忠诚（1958－），男，江苏淮安人，教授，目前主要研究方向为微流控光学技术及微流控器件；孙开文（1989－），男，湖北孝感人，硕士，主要研究方向为微流控光学技术及微流控器件，E-mail: kaiwensunzhe@163.com。

网络出版时间：2017-07-31 11:32

http://kns.cnki.net/kcms/detail/51.1241.TN.20170731.1132.014.html