比较逻辑斯蒂与地理加权逻辑斯蒂回归模型在福建林火发生的适用性

梁慧玲,王文辉,郭福涛,林芳芳,林玉蕊,*

1 福建农林大学计算机与信息学院,福州 350002 2 福建农林大学林学院,福州 350002 3 漳州理工职业学院,漳州 363000



比较逻辑斯蒂与地理加权逻辑斯蒂回归模型在福建林火发生的适用性

梁慧玲1,2,3,王文辉2,郭福涛2,林芳芳1,林玉蕊1,*

1 福建农林大学计算机与信息学院,福州 350002 2 福建农林大学林学院,福州 350002 3 漳州理工职业学院,漳州 363000

林火预测预报是科学有效进行林火管理的前提,是林业管理部门和科研工作者的广泛关注的领域。逻辑斯蒂回归(Logistic Regression, LR)是目前国内外广泛应用于森林火灾预测的模型方法,然而近年来有学者发现该方法没有充分考虑林火影响因子的空间相关性和异质性,从而导致模型拟合结果偏差。地理加权逻辑斯蒂回归(Geographically weighted logistic regression, GWR)模型考虑到了模型变量之间的空间相关性,有效提高的模型的拟合能力。为探讨GWLR模型在福建林火预测上的适用性,本研究应用LR和GWLR两种方法分别建立福建省森林火灾与气象因子的预测模型,通过模型拟合能力对比,判断在GWLR的适用性。研究以2000—2005年福建地区森林火灾卫星火点数据和每日气象因子为基础,将全样本分为60%的建模数据和40%的校验数据,并重复5次,建立5个样本组。选择在5个样本组中3个及以上表现显著的变量进入最终模型。研究结果表明GWLR在模型拟合度、模型残差、空间自相关性以及预测准确率等方面均优于LR模型,说明充分考虑模型变量的空间异质性有助于提高模型的预测精度,同时也验证了GWLR在福建地区林火预测上的适应性。此外,模型参数结果显示,“日最高地表气温”、“日最低地表气温”、“日平均风速”、“24小时降水量”、“日最高本站气压”、“日照时数”、“日最高气温”和“日最小相对湿度”8个因子对福建省林火发生有显著影响,研究结论为福建地区林火预测预报提供了新的方法。

林火预测；空间异质性；逻辑斯蒂回归；地理加权逻辑斯蒂回归

林火是是森林生态系统的重要影响因子,对森林资源与环境造成破坏也会威胁人类生命财产安全[1- 3]。判定林火发生的影响因子,建立准确的林火预测预报模型对林火管理工作至关重要。目前,国内外有关林火发生的预测模型和影响因子分析已大量开展,主要模型方法为人工神经网络[4]、最大熵算法[5,6]、分类树[7]、泊松回归、负二项回归、零膨胀泊松、零膨胀负二项以及逻辑斯蒂回归模型[8- 11]等,其中逻辑斯蒂模型应用最为广泛。然而以上所有模型均假设因变量与自变量之间的关系是空间平稳的,即模型参数在整个研究区域上是一个不变的常数,通常建模的结果是一套模型参数应用于整个研究区域,也称之为全局模型。然而,随着研究的深入,很多学者发现区域的空间异质性是不容忽略的。林火与影响因子之间的关系在空间上是非平稳的,具有很强的异质性[12- 14],因此,以往的全局模型在林火预测预报上可能会产生较大误差。

地理加权回归模型(GWR)考虑了地理空间因素的影响,该模型将一个大的数据集分成了若干小区域,减少了各个模型间的差异性,有助于提高模型精度,可以用来解决空间的平稳性问题。目前,地理加权回归模型主要应用在生态学、经济学和社会科学等领域[15- 19]。近年来,国外已有少数学者将该模型的拓展模型即地理加权逻辑斯蒂模型(GWLR)应用于森林火灾的预测预报及林火影响因子的空间分析上,并且表现出较好的拟合效果[12- 14]。由于该模型强调自变量与因变量关系的空间异质性,因此模型在不同区域的适用性可能有较大差异。为了探讨GWLR模型对我国亚热带地区林火预测预报的适用性,且由于2000—2005年福建省的林火发生既不是太多,也不是很少,比较有代表性,因此本文以福建省2000—2005年卫星火点数据为基础,选取每日气象数据为自变量因子,对模型的拟合能力进行分析,并与传统全局逻辑斯蒂回归模型进行对比,探讨地理加权回归模型在林火预测预报上的适用性。

1 材料和方法

1.1 研究区域概况

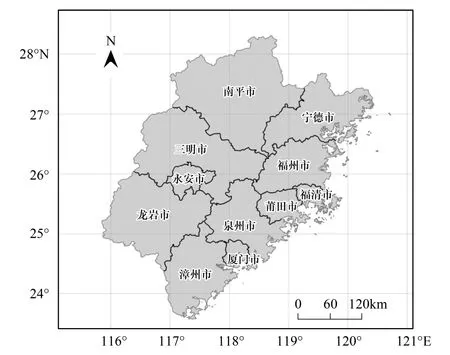
图1 研究区域示意图Fig.1 The study area

福建省位于我国东南沿海地区,介于北纬23°33′—28°20′、东经115°50′—120°40′之间(图1)。根据第八次全国森林资源清查结果显示,福建省林业用地面积926.82万hm2,森林面积801.27万hm2,人工林面积377.69万hm2,森林覆盖率65.95%,森林蓄积量60796.15万m3[20],是我国南方重点林区的省份之一。但是,也是我国森林火灾的高发区。1951—1987年,全省共发生6.2万次的森林火灾,受害山林面积有150万hm2,平均每年森林火灾0.1万次,受害山林面积4万hm2,占全省年平均造林面积的25%—33.3%[21]；1998—2007年间,福建省共发生森林火灾4504起,火场面积累计达79,572hm2,受害森林面积累计达55485.6 hm2,共损失了97万m3的林木蓄积量,其中2004年发生了1164次火灾,1998年林火发生次数最少,为156次；仅10年就发生了40次重大火灾[22]。福建省森林火灾问题尤为严峻。

1.2 数据来源与处理

1.2.1 数据来源

福建省2000—2005年的林火发生数据(包括起火时间、起火原因、起火地理坐标等)来源于林业科学数据中心(http://www.cfsdc.org/indexAction.action?classId=1)提供的卫星火点解译数据；历史气象数据来源于中国气象数据共享网络(http://cdc.cma.gov.cn/),为2000—2005年福建省内22个国家级气象站的每日气象数据,一共包22个气象因子。由于仪器设备和气象站点变化等原因,造成部分数据缺失,且无法修补。因此,本研究对气象数据进行预处理,剔除部分缺失数据,剩下的气象因子包括日平均地表气温(℃),日最高地表气温(℃),日最低地表气温(℃),日平均风速(m/s),日最大风速(m/s),24小时降水量(mm),日平均本站气压(hPa),日最高本站气压(hPa),日最低本站气压(hPa),日照时数(hour),日平均气温(℃),日最高气温(℃),日最低气温(℃),日平均相对湿度(%),日最小相对湿度(%)共15个气象因子。

1.2.2 数据处理

本文以2000—2005年的卫星火点数据为基础,从中随机选取60%的训练样本(5210个林火数据)来构建模型,剩下40%的测试样本(3473个林火数据)用来检验模型。同时,为了避免样本分布对试验结果的影响,本文重复5次试验,即重复5次训练样本和测试样本的随机划分,选择5次试验中出现3次或以上的显著变量进入全样本数据拟合。

本文分别应用SPSS 19.0和GWR4软件对逻辑斯蒂回归模型和地理加权逻辑斯蒂回归模型进行拟合,并应用Rookcase软件对模型残差进行空间自相关分析。

1.3 研究方法

1.3.1 二项逻辑斯蒂回归模型

(1)多重共线性(Multicollinearity)是指在线性回归模型中,自变量之间存在精确的相关关系或者高度相关关系的现象。

本文运用方差膨胀因子(the variance inflation factor,VIF)诊断法对林火发生的驱动因子进行共线性检验。方差膨胀因子最早是由Marquardt于1960年引入的,第i个变量的方差膨胀系数的表达式为

(3)

(2)逻辑斯蒂回归模型属于广义线性回归模型,对于只有两种分类结果的分类因变量,可以应用二元逻辑斯蒂回归模型进行建模分析,其预测值为在[0,1]之间的预测概率。逻辑斯蒂模型是目前国内外应用最广的用于预测林火发生概率的模型。设有林火发生(Y=1)的概率为P,则无林火发生(Y=0)的概率为(1-P),则有林火发生的概率

(1)

式中,z为解释变量x1,x2,...,xn的线性函数,

z=α0+α1x1+α2x2+...+αnxn

(2)

式中,α0,α1,α2,...,αn为各个解释变量的回归系数。

对P进行Logit变换,即将P变换为ln[P/(1-P)],则有

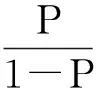
(3)

最后,运用极大似然估计法可求得模型的参数估计系数α0,α1,α2,...,αn[23- 25]。

1.3.2 地理加权逻辑斯蒂回归模型

由于地理位置的不同而引起变量之间的关系或者结构发生变化的现象称为空间非平稳性(spatialnonstationarity)。地理加权逻辑斯蒂回归模型是传统逻辑斯蒂回归模型的扩展,考虑了空间位置因素,利用加权最小二乘法对每一个坐标点进行参数估计,对参数的估计是局部而非全局的,每一个位置均有相应的参数估计系数[26-27]。地理加权逻辑斯蒂回归模型(GWLR)的表达式为：与逻辑斯蒂模型相同,位置i有林火发生(Y=1)的概率为P,则无林火发生(Y=0)的概率为(1-P),则位置i有林火发生概率

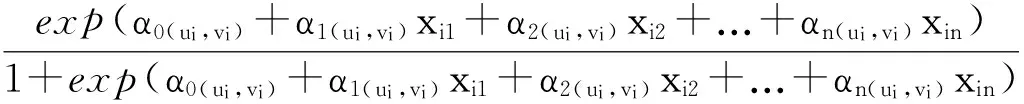
式中,z=α0(ui,vi)+α1(ui,vi)xi1+α2(ui,vi)xi2+...+αn(ui,vi)xin。

经Logit变换,有

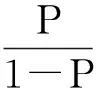
最后,运用加权最小二乘法可求得位置i的局部回归模型的参数估计系数,即

1.3.3 模型预测准确率计算

本文根据ROC曲线分析法所计算出来的敏感性值和特异性值,可求得约登指数,即约登指数=敏感性值+特异性值-1,进而计算出福建省林火发生的最佳临界值(cut-off值),如果林火发生的预测概率大于该临界值则认为有林火发生,小于该临界值则认为无林火发生,从而根据模型所计算出来的林火发生次数与实际值进行比较,进而计算出LR模型和GWLR模型模型对林火发生与否的正确判别率。

1.3.4 模型空间自相关检验Moran′sI

本文应用全局Moran′sI指数计算残差(残差=观测值-预测值)的空间自相关来对模型进行评价,全局Moran′sI指数的值越小,说明残差的空间依赖程度越低,模型考虑了更多的空间结构问题,模型的效果越好。

全局Moran′sI指数的计算公式为：

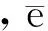
2 结果与分析

2.1 模型拟合结果与分析

2.1.1 多重共线性诊断结果

多重共线性诊断结果显示,变量“日平均地表气温”、“日平均本站气压”、“日最低本站气压”、“日平均气温”、“日最低气温”等5个变量均存在共线性关系,将这5个变量剔除之后,用剩下的10个自变量构建LR模型和GWLR模型。

2.1.2 LR模型拟合结果

本文应用LR模型和“wald向前”原则对5个训练样本进行拟合计算,得到5个不同的特征变量子集,然后在5个特征变量子集中选择出现3次或3次以上的特征变量进入全样本数据的拟合计算(表1)。

表1 LR模型特征变量选择结果

+表示变量在模型里面；-表示变量不在模型里面

由表1可知,“日最高地表气温”、“日最低地表气温”、“日平均风速”、“日降水量”、“日最高本站气压”、“日照时数”、“日最高气温”和“日最小相对湿度”等8个变量进入了全样本数据的拟合阶段,且除了“日最高本站气压”和“日最小相对湿度”在5个中间模型特征变量选择结果中出现4次以外,其他6个变量均出现了5次。表2为8个显著变量的全样本数据拟合结果,结果显示各变量与林火发生具有显著相关性。其中“日最高地表气温”、“日平均风速”、“日最高本站气压”、“日照时数”和“日最高气温”等5个气象因子与森林火灾呈正相关关系,“日最低地表气温”、“日降水量”和“日最小相对湿度”3个气象因子与森林火灾呈负相关关系,且这8个气象因子对林火发生均有显著的影响。

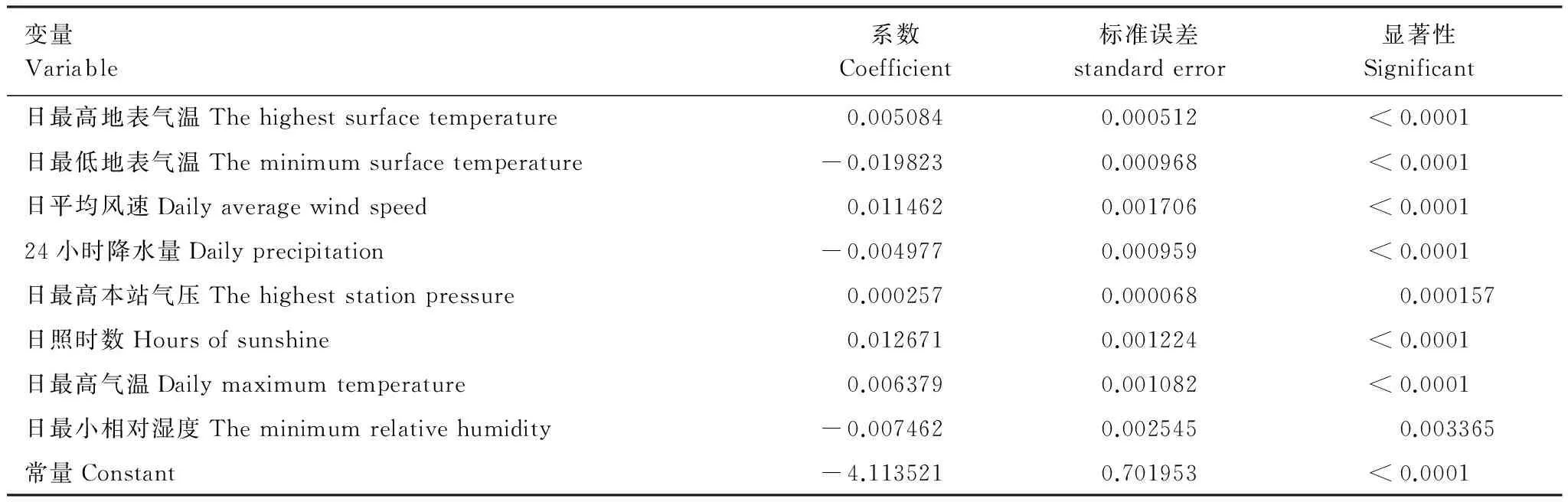
表2 全样本数据的LR模型参数拟合结果

2.1.3 GWLR模型拟合结果

首先假设模型的数据结构是空间非平稳的,对5个训练样本进行模型拟合,然后对因变量与解释变量之间的关系的空间非平稳性进行检验。如果“某解释变量的估计系数的四分位数范围大于LR模型中该解释变量的估计系数的±1标准差范围”[13,29],则认为该解释变量是显著空间非平稳变量(以样本1为例,LR模型和GWLR模型系数估计结果见附表1)。最后在5个训练样本中选择出现3次或3次以上的非平稳变量进入全样本数据的拟合阶段,并作为全样本数据模型的非平稳项,而其他平稳变量则作为全样本数据模型的平稳项。检验结果显示除了“日最低相对湿度”在5个中间模型中有1次被检验为空间平稳变量之外,其他9个气象因子在5个中间模型中均被检验为空间非平稳变量(附表2)。全样本数据的GWLR模型参数拟合结果如表3所示。

表3 全样本数据的GWLR模型参数估计

注：系数的最大和最小值若符号相同表示该变量在整个研究区域上与林火的相关性一致,反之表示变量在整个区域上与林火的相关性具有正负差异

表3显示,除“日最低地表气温”在整个研究区域上均与林火发生呈负相关关系之外,其他9个气象因子在整个研究区域上均在正相关和负相关之间变化。为更好体现GWLR模型各变量系数的局部变化,本文运用ArcGIS 10.2对各变量模型估计系数进行空间插值(图2)。图2表明GWLR模型的估计系数随空间位置变化而变化,具有明显的空间异质性。

图2 变量系数分布图Fig.2 Variable coefficient distribution

此外,对各变量估计系数的t检验值进行空间插值,若估计系数t检验值的绝对值小于1.96,则表示估计系数在研究区域上不显示,若t检验值小于-1.96或大于1.96,说明估计系数显著。图3表明模型变量的估计系数的显著性也具有很强的空间异质性。

图2,图3综合显示“日最低地表气温”在整个研究区域上均与林火发生呈负相关关系,且该因子的估计系数在整个研究区域上均显著；“24小时降水量”与林火发生呈显著负相关系数；“日照时数”和“日最高气温”与林火发生呈显著正相关关系；“日最高本站气压”与林火发生存在正负两种相关性,但以正相关为主,主要分布在福建北部和南部地区；“日平均相对湿度”在南平市北部地区和龙岩市大部分地区与林火呈显著的负相关关系,仅在三明与南平市交界处存在小块正相关区域；“日最小相对湿度”在龙岩市西南地区存在显著正相关系数,在三明市和永安市交界处及厦门市和漳州市的小部分沿海地区存在显著的负相关系数；“日平均风速”在福建省西部和中部地区与林火发生呈显著正相关,而“日最大风速”在西部和中部地区与林火发生则呈显著负相关。

2.2 模型评价

本文将全样本分成60%的训练样本(用于建模)和40%的测试样本(模型检验)。应用最小信息准则(AIC)、残差平方和(SSE)和ROC曲线(ROC)下的面积AUC值(AUC)等统计量和模型的预测准确率对LR和GWLR模型进行对比评价。

模型拟合统计结果表明,对比传统逻辑斯蒂回归模型,地理加权逻辑斯蒂回归模型具有更小的AIC和SSE值,和更大的AUC值以及更高的模型预测准确率(表4)。表4显示,LR模型的预测准确率为74.2%—76.2%小于GWLR模型(77.1%—78.6%)。

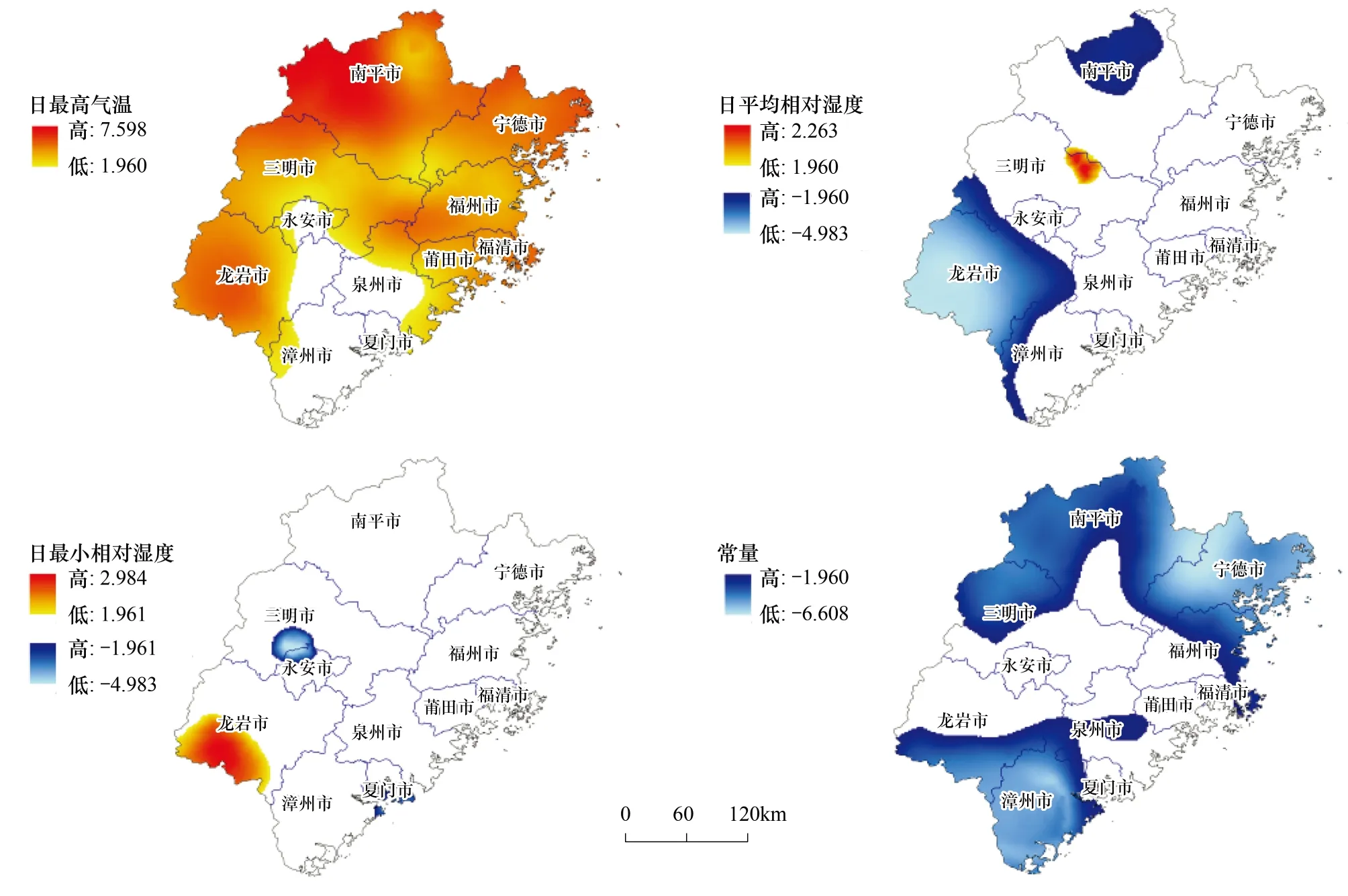
图3 变量系数显著性分布图Fig.3 Significant distribution of variable coefficient正显著相关性用暖色调表示,负显著相关性用冷色调表示

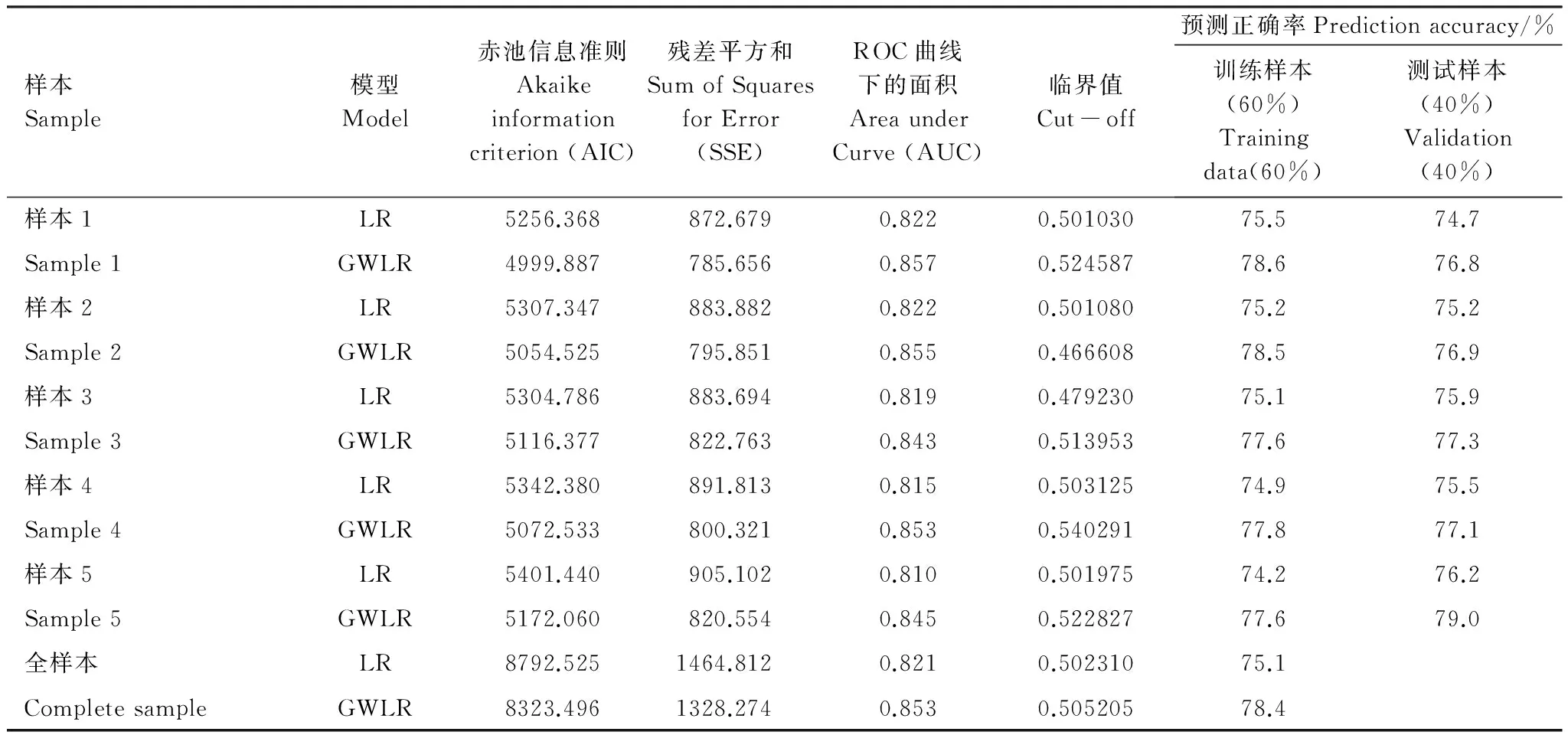
样本Sample模型Model赤池信息准则Akaikeinformationcriterion(AIC)残差平方和SumofSquaresforError(SSE)ROC曲线下的面积AreaunderCurve(AUC)临界值Cut-off预测正确率Predictionaccuracy/%训练样本(60%)Trainingdata(60%)测试样本(40%)Validation(40%)样本1LR5256.368872.6790.8220.50103075.574.7Sample1GWLR4999.887785.6560.8570.52458778.676.8样本2LR5307.347883.8820.8220.50108075.275.2Sample2GWLR5054.525795.8510.8550.46660878.576.9样本3LR5304.786883.6940.8190.47923075.175.9Sample3GWLR5116.377822.7630.8430.51395377.677.3样本4LR5342.380891.8130.8150.50312574.975.5Sample4GWLR5072.533800.3210.8530.54029177.877.1样本5LR5401.440905.1020.8100.50197574.276.2Sample5GWLR5172.060820.5540.8450.52282777.679.0全样本LR8792.5251464.8120.8210.50231075.1CompletesampleGWLR8323.4961328.2740.8530.50520578.4

2.3 残差分析

根据两个模型对5样本和全样本数据的拟合结果,分别绘制模型的残差图(图4)。图4表明GWLR模型具有更小的残差。

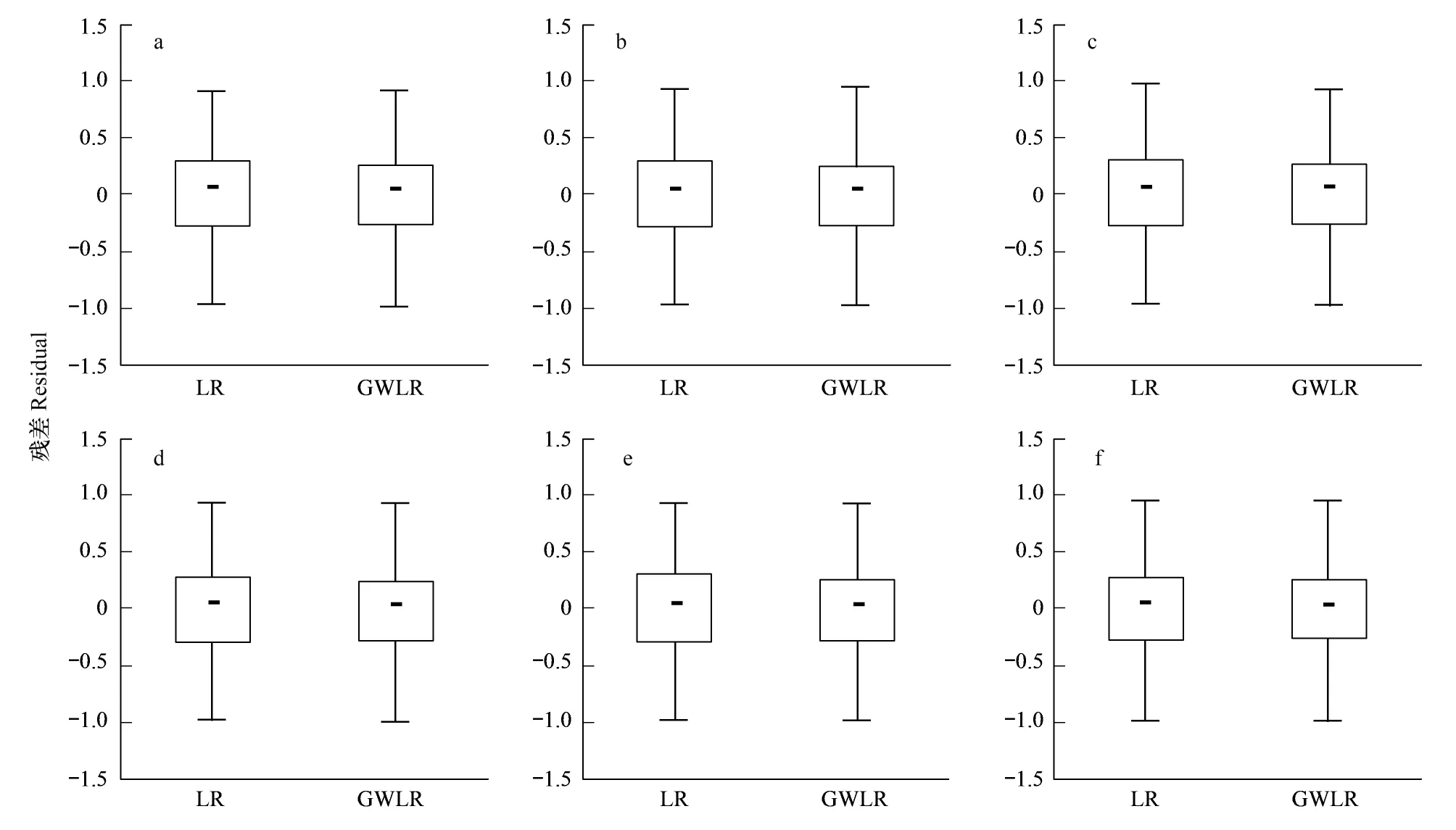
图4 模型残差箱形图Fig.4 Box figure the model residuals

全样本模型的残差空间自相关(图5)结果显示GWLR模型的Moran′s I值比LR模型小,说明与LR模型相比,GWLR模型在福建省林火发生与否的判别问题中考虑了更多的空间自相关问题,GWLR模型对福建省林火发生的拟合效果较好。

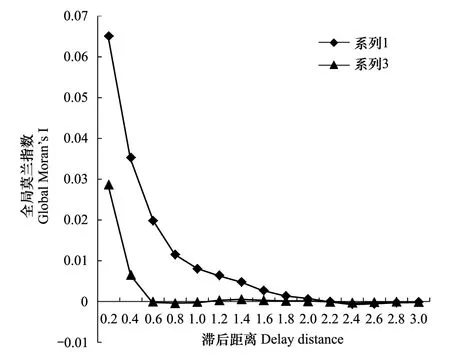
图5 全样本模型的残差空间自相关Fig.5 Final sample of residual spatial autocorrelation

3 讨论

气候条件的变化对森林火灾的发生具有重要的影响,因此,本文基于气象因子应用传统的逻辑斯蒂回归模型和地理加权逻辑斯蒂回归模型对福建省2000—2005年的林火数据进行分析,对两种模型的预测能力以及对模型在森林火灾应用方面的适用性进行分析。模型变量选择结果显示,“日最高地表气温”、“日最低地表气温”、“日平均风速”、“24小时降水量”、“日最高本站气压”、“日照时数”、“日最高气温”和“日最低相对湿度”等8个变量均是LR模型和GWLR模型的全样本特征变量,说明这8个气象因子是福建省森林火灾的主要影响因子。气温的变化会使可燃物的湿度发生变化,改变火灾的气候条件,从而对森林火灾产生影响。我们的研究结果显示,“气温”对森林火灾的发生具有重要的影响,这与Liu[32]和Hu和Zhou[33]的研究结果一致；相对湿度是反应林内可燃物含水量的一个重要指标,对林火发生有重要影响。我们的研究结果表明“相对湿度”对林火发生有重要的影响,与Zhang[24]的研究结果一致。通常一个地区重特大火灾的发生,与最大风速是相关,但是,本文在对气象因子进行分析时,逻辑斯蒂回归模型却将“日最大风速”剔除,而地理加权逻辑斯蒂回归模型回归模型则显示“日最大风速”是一个空间非平稳变量,因此,模型变量的选择是否理想与模型的选择相关。此外,本研究并没有考虑地形、植被类型、人为活动等条件对森林火灾的影响,因此可能会对研究结果产生偏差。

传统的逻辑斯蒂回归模型假设空间变量都是平稳变量,忽略了模型变量的空间异质性,模型的拟合结果无法全面反映变量的空间关系,而本文的研究结果显示,影响福建省林火发生的气象因子具有明显的空间异质性,且模型评价结果显示与传统的逻辑斯蒂回归模型相比,地理加权逻辑斯蒂回归模型的拟合效果较好,这与Saefuddin[31]、Koutsias[12]、Wu和Zhang[28]等前人的研究结果一致,表明在对具有空间结构的数据进行拟合分析时,应考虑空间地理位置变化对因变量结果的影响。

4 结论

本文应用逻辑斯蒂回归模型和地理加权逻辑斯蒂回归模型对福建省森林火灾空间格局和气象影响因子进行分析,并对两种模型的拟合效果进行研究,结果表明：(1)“日最高地表气温”、“日最低地表气温”、“日平均风速”、“24小时降水量”、“日最高本站气压”、“日照时数”、“日最高气温”和“日最低相对湿度”等8个变量是3个模型的共同变量,是影响福建省林火发生的主要气象因子；(2)在福建省林火发生的分类判别中,与传统的逻辑斯蒂回归模型相比,地理加权逻辑斯蒂回归模型的拟合效果更好,更适合福建省森林火灾的数据结构。

[1] Grogan P, Burns T D, Chapin F S. Fire effects on ecosystem nitrogen cycling in a Californian bishop pine forest. Oecologia, 2000, 122(4): 537- 544.

[2] Liu H P, Rerson J T, Lindfors J, Chapin F S. Changes in the surface energy budget after fire in boreal ecosystems of interior Alaska: An annual perspective. Journal of Geophysical Research Atmospheres, 2005, 110(D13): D13101.

[3] Chas-Amil M L, Touza J, Prestemon P. Spatial distribution of human-caused forest fires in Galicia (NW Spain). Ecology and the Environment, 2010, 137: 247- 258.

[4] Bisquert M, Caselles E, Sánchez J M, Caselles. Application of artificial neural networks and logistic regression to the prediction of forest fire danger in Galicia using MODIS data. International Journal of Wildland Fire, 2012, 21(8): 1025- 1029.

[5] Parisien M A, Snetsinger S, Greenberg J A, Nelson C R, Schoennagel T, Dobrowski S Z, Moritz M A. Spatial variability in wildfire probability across the western United States. International Journal of Wildland Fire, 2012, 21(4): 313- 327.

[6] Renard Q, Pélissier R, Ramesh B R, Kodandapani N. Environmental susceptibility model for predicting forest fire occurrence in the Western Ghats of India. International Journal of Wildland Fire, 2012, 21(4): 368- 379.

[7] Lozano F J, Suárez-Seoane S, Kelly M, Luis E. A multi-scale approach for modeling fire occurrence probability using satellite data and classification trees: A case study in a mountainous Mediterranean region. Remote Sensing of Environment, 2008, 112(3): 708- 719.

[8] 郭福涛, 苏漳文, 马祥庆, 宋禹辉, 孙龙, 胡海清, 杨婷婷. 大兴安岭塔河地区雷击火发生驱动因子综合分析. 生态学报, 2015, 35(19): 6439- 6448.

[9] 郭福涛, 胡海清, 金森, 马志海, 张扬. 基于负二项和零膨胀负二项回归模型的大兴安岭地区雷击火与气象因素的关系. 植物生态学报, 2010, 34(5): 571- 577.

[10] 秦凯伦, 郭福涛, 邸雪颖, 孙龙, 宋禹辉, 吴瑶, 潘建峰. 大兴安岭塔河地区林火发生的优势预测模型选择. 应用生态学报, 2014, 25(3): 731- 737.

[11] 郭福涛, 胡海清, 马志海, 张扬. 不同模型对拟合大兴安岭林火发生与气象因素关系的适用性. 应用生态学报, 2010, 21(1): 159- 164.

[12] Koutsias N, Martínez J, Chuvieco E, Alligöwer B. Modeling wildland fire occurrence in southern europe by a geographically weighted regression approach // Proceedings of the 5th International Workshop on Remote Sensing and GIS Applications to Forest Fire Management: Fire Effects Assessment. Spain: Universidad de Zaragoza, 2005: 57- 60.

[13] Martínez-Fernández J, Chuvieco E, Koutsias N. Modelling long-term fire occurrence factors in Spain by accounting for local variations with geographically weighted regression. Natural Hazards and Earth System Sciences, 2013, 13(2): 311- 327.

[14] Rodrigues M, De La Riva J, Fotheringham S. Modeling the spatial variation of the explanatory factors of human-caused wildfires in Spain using geographically weighted logistic regression. Applied Geography, 2014, 48: 52- 63.

[15] Wang Q, Ni J, Tenhunen J. Application of a geographically-weighted regression analysis to estimate net primary production of Chinese forest ecosystems. Global Ecology and Biogeography, 2005, 14(4): 379- 393.

[16] Tu J. Spatially varying relationships between land use and water quality across an urbanization gradient explored by geographically weighted regression. Applied Geography, 2011, 31(1): 376- 392.

[17] Propastin P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 2012, 18: 82- 90.

[18] Freedman R, Roy S S. Spatial patterning ofMantabirostrisin United States east coast offshore habitat. Applied Geography, 2012, 32(2): 652- 659.

[19] Aguilar G D, Farnworth M J. Stray cats in Auckland, New Zealand: discovering geographic information for exploratory spatial analysis. Applied Geography, 2012, 34: 230- 238.

[20] 国家林业局. 第八次全国森林资源清查结果. 林业资源管理, 2014, (1): 1- 2.

[21] 李兆明, 高兆蔚. 福建森林火险天气等级预测预报方法. 福建林学院学报, 1989, 9(2): 172- 176.

[22] 朱学平, 何东进, 丁福立, 洪伟, 游巍斌, 纪志荣. 基于突变级数法的福建省森林火灾评价分析. 福建林学院学报, 2011, 31(4): 295- 299.

[23] Garcia C V, Woodard P M, Titus S J, Adamowicz W L, Lee B S. A logit model for predicting the daily occurrence of human caused forest-fires. International Journal of Wildland Fire, 1995, 5(2): 101- 111.

[24] Zhang Z X, Zhang H Y, Zhou D W. Using GIS spatial analysis and logistic regression to predict the probabilities of human-caused grassland fires. Journal of Arid Environments, 2010, 74(3): 386- 393.

[25] del Hoyo L V, Isabel M P M, Vega F J M. Logistic regression models for human-caused wildfire risk estimation: analysing the effect of the spatial accuracy in fire occurrence data. European Journal of Forest Research, 2011, 130(6): 983- 996.

[26] 郭含茹, 张茂震, 徐丽华, 袁振花, 陈田阁. 基于地理加权回归的区域森林碳储量估计. 浙江农林大学学报, 2015, 32(4): 497- 508.

[27] 肖燕婷, 田铮, 魏岳嵩. 时空地理加权回归模型的时空非平稳性检验. 系统工程理论与实践, 2013, 33(6): 1537- 1542.

[28] Wu W, Zhang L J. Comparison of spatial and non-spatial logistic regression models for modeling the occurrence of cloud cover in northeastern Puerto Rico. Applied Geography, 2013, 37: 52- 62.

[29] Zhang H J, Qi P C, Guo G M. Improvement of fire danger modelling with geographically weighted logistic model. International Journal of Wildland Fire, 2014, 23(8): 1130- 1146.

[30] Rodrigues M, De La Riva J. An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environmental Modelling & Software, 2014, 57: 192- 201.

[31] Saefuddin A, Setiabudi N A, Fitrianto A. On comparison between logistic regression and geographically weighted logistic regression: with application to Indonesian poverty data. World Applied Sciences Journal, 2012, 19(2): 205- 210.

[32] Liu Z H, Yang J, Chang Y, Weisberg P J, He H S. Spatial patterns and drivers of fire occurrence and its future trend under climate change in a boreal forest of Northeast China. Global Change Biology, 2012, 18(6): 2041- 2056.

[33] Hu T Y, Zhou G S. Drivers of lightning-and human-caused fire regimes in the Great Xing′an Mountains. Forest Ecology and Management, 2014, 329: 49- 58.

附表：

Comparing the application of logistic and geographically weighted logistic regression models for Fujian forest fire forecasting

LIANG Huiling1,2,3, WANG Wenhui2, GUO Futao2, LIN Fangfang1, LIN Yurui1,*

1CollegeofComputerandInformationScience,FujianAgricultureandForestryUniversity,Fuzhou350002,China2CollegeofForestry,FujianAgricultureandForestryUniversity,Fuzhou350002,China3ZhangzhouInstituteOfScience&Engineering,Zhangzhou363000,China

Forest fire forecasting is a key component of effective and science-based forest management and has been comprehensively addressed in the scientific literature. The logistic regression (LR) technique has been used in forest fire prediction models. However, some scholars have recently reported that the technique does not adequately consider the spatial correlation and heterogeneity of fire impact factors, which results in poorly fitting models. In contrast, geographically weighted logistic regression (GWR) models consider the spatial correlation of model variables, which improves the model′s goodness of fit. In order to explore the applicability of the GWLR model in Fujian forest fire forecasting, the present study used both the LR and GWLR methods to establish forecast model for forest fires and meteorological factors in Fujian Province, and the model fitting ability of two models were compared. Based on the forest fire and meteorological data for Fujian from 2000 to 2005, the original dataset was randomly divided into training (60%) and validation (40%) samples, with five replications and five sample groups, and predictors that were significant (ɑ=0.05) for at least three of the five sample groups were included in the final models. The goodness of fit, residual error, spatial autocorrelation, and prediction accuracy of the GWLR model were all better than those of the LR model, and the GWLR comprehensively explained the spatial heterogeneity of model variables and helped to improve the prediction accuracy of the model. The study also verified the suitability of the GWLR model on the forest fire forecasting in Fujian area. In addition, the results also indicated that the occurrence of Fujian forest fires is significantly affected by eight parameters, including minimum and maximum surface temperature, daily average wind speed, daily precipitation, highest station pressure, hours of sunshine, daily maximum temperature, and daily minimum relative humidity. Therefore, the GWLR model may provide a new technique for the prediction of forest fires in Fujian Province.

forest fire forecast; spatial heterogeneity; logistic regression; geographically weighted logistic regression(GWLR)

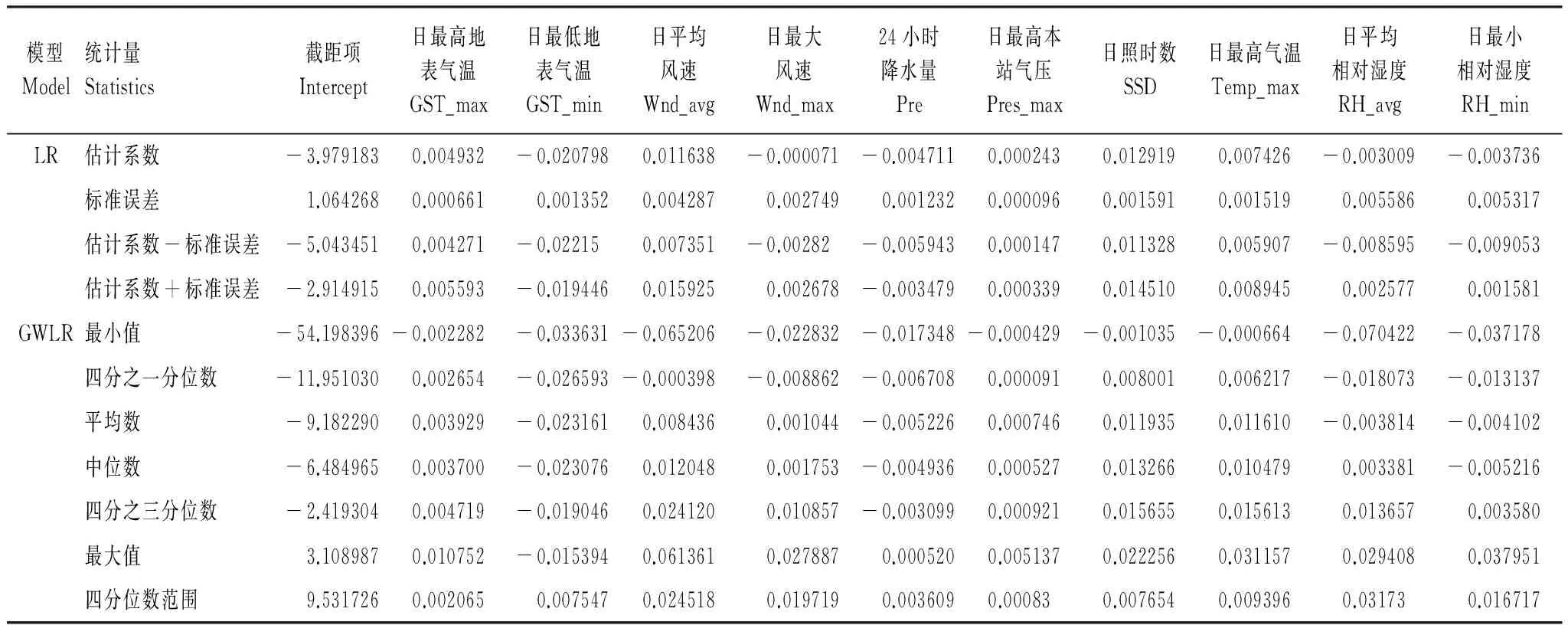
附表1 LR模型和GWLR模型的系数估计(样本1)

附表2 GWLR模型空间(非)平稳变量检验结果

+表示该变量是空间非平稳变量;-表示该变量是空间平稳变量

国家自然科学基金(31400552)；福建省自然科学基金(2015J05049)；福建省教育厅资助省属高校专项(JK2014012)

2016- 05- 01;

2017- 01- 16

10.5846/stxb201605010828

*通讯作者Corresponding author.E-mail: yrlin@fafu.edu.cn

梁慧玲,王文辉,郭福涛,林芳芳,林玉蕊.比较逻辑斯蒂与地理加权逻辑斯蒂回归模型在福建林火发生的适用性.生态学报,2017,37(12):4128- 4141.

Liang H L, Wang W H,Guo F T, Lin F F, Lin Y R.Comparing the application of logistic and geographically weighted logistic regression models for Fujian forest fire forecasting.Acta Ecologica Sinica,2017,37(12):4128- 4141.