应变式传感器的信号隔离及数据重构*

乔爱民,何博侠,黄迎辉,王艳春

(1.蚌埠学院电子与电气工程学院,安徽 蚌埠 233000;2.南京理工大学机械工程学院,南京 210094)



应变式传感器的信号隔离及数据重构*

乔爱民1*,何博侠2,黄迎辉1,王艳春1

(1.蚌埠学院电子与电气工程学院,安徽 蚌埠 233000;2.南京理工大学机械工程学院,南京 210094)

采用较高频率的周期性方波信号作为载波及解调信号,通过调制与同步解调技术对应变式传感器的输出模拟信号进行变压器式隔离。将隔离后的模拟信号及传感器使用环境温度对应的数字量作为输入变量,传感器的实际负载作为输出变量,利用移动最小二乘回归(MLSR)重构传感器所受负载与使用温度及隔离信号之间的数据模型。试验结果表明,采用调制及同步解调技术的模拟信号变压器式隔离电路具有良好的温度稳定性,利用MLSR建立的传感器数据重构模型拥有比传统最小二乘回归(LSR)更高的精度,在试验条件下的温度变化范围内,采用变压器式隔离电路得到的模拟信号隔离相对误差低于±0.2%,基于MLSR的传感器数据重构模型的负载检测相对误差低于±0.07%。

应变式传感器;模拟信号隔离;调制与解调;数据重构;移动最小二乘回归

应变式传感器是基于弹性体弹性变形过程中的电阻应变效应制成的传感器,目前被广泛应用于力、扭矩、强度等及与其相关的非电物理量检测[1-2]。应变式传感器内部通常将感受应力变化的应变片组建成惠斯登电桥,当采用直流电源供电时,传感器输出差动电压信号。

在很多的传感器应用现场,传感器容易受到诸多的干扰信号影响,而信号隔离是一种非常有效的抗干扰措施[3-7]。目前常用的模拟信号隔离方法有:①采用线性光电耦合器进行隔离,如采用基于线性光耦HCNR201的隔离电路实现模拟信号隔离[3-4]。②采用价格昂贵的隔离放大器或商品化的隔离变送器进行模拟信号的隔离放大[5-7]。③对模拟信号进行AD转换后再通过数字光电耦合器对转换后的数字量进行隔离。④采用调制解调的方法将模拟信号进行变压器式隔离。其中方法①由于采用的是光电耦合器件,温度稳定性较差,方法②及方法③的隔离成本高,不便于模拟信号隔离的普及应用,而方法④通过调制技术将低频的传感器输出信号推至高频区,可有效提高信噪比[8-9],同时,其温度稳定性及重复性等性能指标要高于光电耦合隔离方式。

传感器的数据重构是通过离散的传感器标定数据,获取传感器的输入输出特征模型的过程。由于传感器在工作过程中除了受到被测物理量的作用外,还受到温度变化的影响,在非恒定温度的应用场合,温度变化导致的传感器特性漂移是传感器在检测过程中主要的误差来源,因此有必要对传感器的特征模型进行包括被测物理量、温度等输入变量的重构。

1 基于周期性方波为载波信号的模拟信号隔离

1.1 传感器输出信号的幅值调制解调及隔离

调制解调包含两个过程:调制和解调,其中调制指的是一个信号的某些参数在另一个信号的控制下而发生变化的过程,前一信号称为载波,后一信号称为调制信号[8-10]。通常情况下,载波信号一般为频率单一的谐波信号,而在应变式传感器应用领域,需要载波信号具有一定的带载能力,周期性的方波信号相比于频率单一的谐波信号,产生的电路结构简单,可利用某些电子元器件如晶体管的饱和特性方便地获得具有一定带载能力的周期性方波信号。

设传感器的输出信号x(t)为带限低频调制信号,且其最高频率为fm,周期性方波信号P(t)为载波信号,其幅值为A,基准频率为fo,且fo远大于fm,按照调制及同步解调原理,调制及解调的过程为如图1所示。

图1中的调制器与解调器实质上是乘法器,用于信号间的时域乘积,可以分别由隔离变压器的一次侧及二次侧配合相关的电路实现,从而可以在对传感器的输出信号进行调制解调的过程中同时实现信号的变压器式隔离。图1中的解调信号和载波信号为同周期且相位相同的方波信号。

图1 传感器信号的调制解调及隔离过程

设周期性方波载波信号在周期[0,1/fo]内的表达式为

(1)

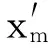
(2)

将载波信号P(t)展开为傅里叶级数

(3)

利用隔离变压器的二次侧及相关电路作为解调器,解调信号的频率与载波信号相同,且假设解调信号的幅值相位和载波信号完全一致,经同步解调后x″m(t)为:

x″m(t)=x′(t)P(t)P′(t)=x′(t)P(t)P(t)

(4)

设x″m(t)的傅里叶变换为X″m(f),x′(t)傅里叶变换为X′(f),P(t)傅里叶变换为Pf(f),则有

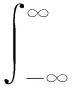
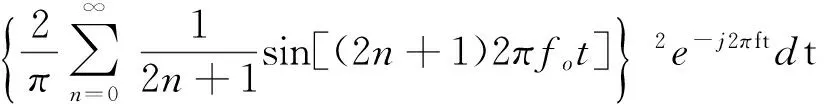
(5)

式中:n为1,2,…。

根据三角函数的正交性、欧拉公式及傅里叶变换的性质,式(5)可写成

X″m(f)=X′(f)*Pf(f)*Pf(f)=

(6)

式中:

δ(2n+1)=δ(f+(2n+1)fo)-δ(f-(2n+1)fo)

式中:δ为单位脉冲函数,Ca为系数项。

式(6)表明,当采用周期性方波信号作为载波及解调信号时,传感器幅值变换后的信号经调制解调后,其傅里叶变换为调幅波的傅里叶变换与方波载波信号及解调信号的各谐波分量傅里叶变换的卷积和的卷积。

由δ函数的卷积特性可知,信号与之卷积的结果等价于将该信号平移至产生δ函数的位置,式(6)表示将X′(f)的幅频谱对应方波的各谐波分量进行连续的两次平移。

令传感器输出信号经幅值变换后x′(t)的幅频谱如图2所示,幅值为1的载波信号及解调信号的谐波分量用双边副频谱表示,其幅频谱如图3所示。

图2 x′(t)的幅频谱

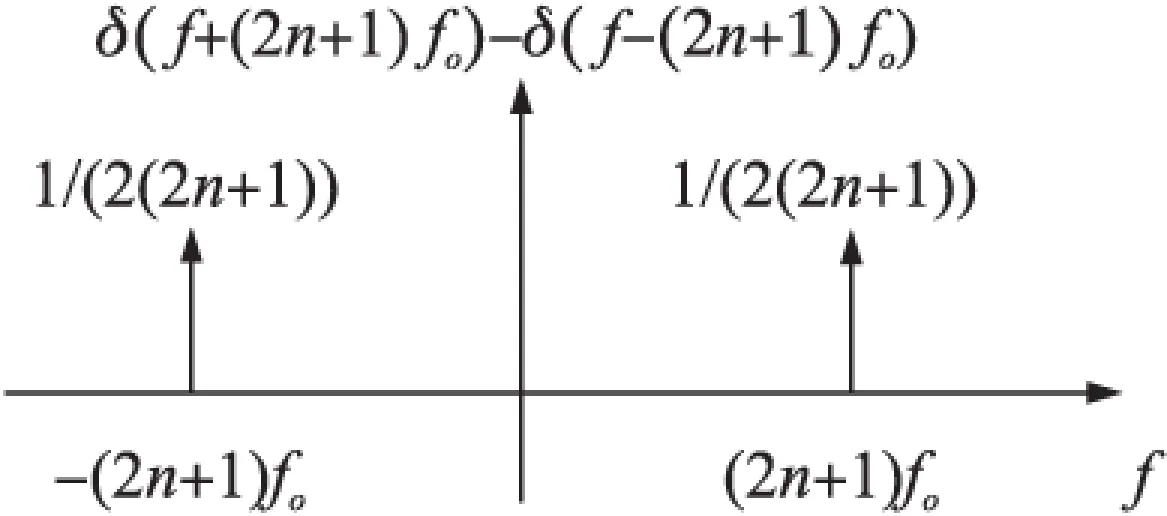
图3 载波及解调信号谐波分量的幅频谱

调制及同步解调后,X′(f)与周期性方波各谐波分量卷积结果的幅频谱为图4及图5所示。

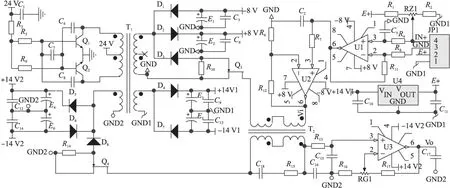
图7 基于载波信号为周期性方波信号的调制及同步解调技术的隔离电路

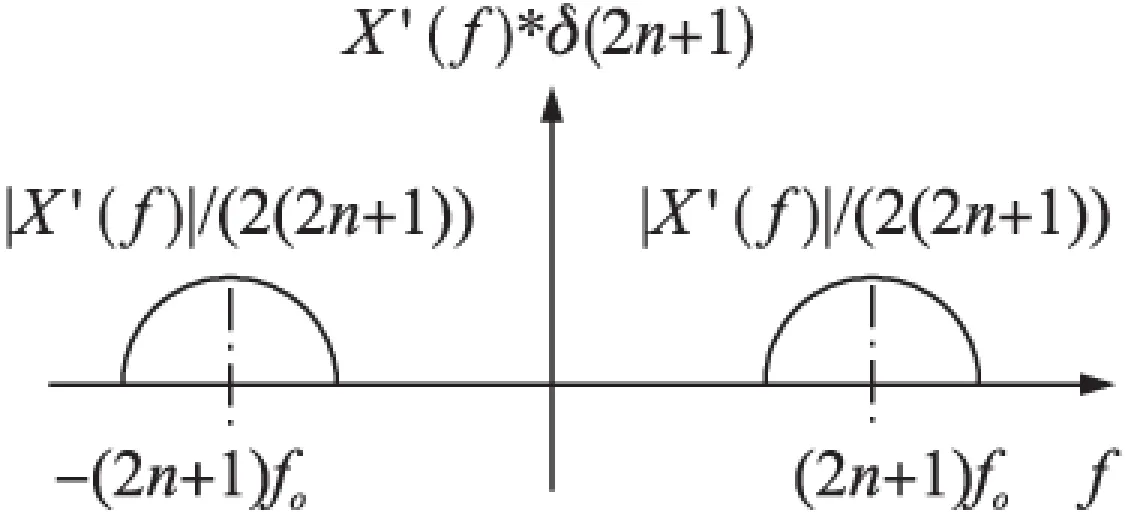
图4 x′(t)调制后幅频谱

图5 x′(t)解调后的幅频谱

因此,X″m(f)的幅频谱为图6所示。

图6 X″m(f)的幅频谱

图6中,XmA的值为

(7)

比较图6及图2的幅频谱,如果将图6中经过调制解调后的高频部分信号通过低通滤波器滤除,剩下的部分就是传感器经幅值变化后的频谱,而由式(7)可知,两者的区别仅仅是频谱的幅值,这可以通过幅值变换使得两者幅值匹配。

1.2 应变式传感器输出信号的变压器式隔离电路

基于上述分析的应变式传感器信号变压器式隔离电路如图7所示。

图7中,由三极管Q1、Q2、C4、C5、R5、R9及T2组成推挽式开关电源电路,其驱动信号为50%占空比的数十kHz周期性方波,在高频变压器T1的次级分别产生三路电源,利用开关二极管D3的单向导通性产生周期性方波信号,驱动Q3产生载波,应变式传感器输出信号经幅值放大后在高频变压器T2的初级通过Q3等相关电路实现与载波信号的时域乘积即调制。由D8对T1的另一次级输出进行单向整流并驱动Q4,产生和载波信号波形、相位及频率一致的解调信号,并在T2的次级实现对调幅信号的解调,由R15、C18及R13、C15和C16组成低通滤波电路,经过隔离后的电压信号Vo与传感器输出信号近似为线性关系。

2 应变式传感器数据重构

在一些应变式传感器应用场合,环境温度变化较大,温度变化会造成传感器的特性漂移,即使不考虑温度变化的影响,传感器输入和输出之间一般呈现非线性关系,当检测精度要求较高时,需要对应变式传感器输入输出之间的模型进行重构。应变式传感器主要用于测量力及与之相关的非电物理量,在实际的检测系统中,常将传感器实际负载作为输出量,而将传感器的电信号作为输入量,因此,将应变式传感器所受负载对应的隔离电信号的AD转换值作为输入变量,并在输入变量中增加传感器工作温度对应的数字量,将应变式传感器的实际负载作为输出变量,建立三者之间的模型,实现对应变式传感器的数据重构。

2.1 用于数据重构的硬件结构

用于应变式传感器数据重构的硬件结构如图8所示。

图8 用于应变式传感器的数据重构的硬件结构框图

将经过变压器式隔离的电信号经过幅值变换后得到Vo,再对之进行AD转换得到离散的转换值xD,由温度传感器采集工作环境温度,其输出对应的数字量为TD,将xD及TD作为输入变量,通过检测系统建立应变式传感器的负载y和xD及TD的数据重构模型。

2.2 基于MLSR的应变式传感器数据重构模型

由于输入变量中添加了传感器的工作环境温度,数据重构模型实质上一方面对应变式传感器的非线性进行修正,另一方面对温度误差进行相应的补偿。目前,有关传感器的数据重构方法,许多学者对之进行了相应的研究,通过引入传感器的使用环境温度输入变量进行传感器的数据模型重构,利用软件补偿环节可有效实现对传感器的非线性及温度漂移进行补偿[11-13],但这些软件补偿方法通常对测试系统的硬件资源和软件资源要求较高,如采用神经网络补偿的方法,可能出现网络不稳定及训练时间长等缺陷[13]。

当考虑温度影响时,传感器的实际负载可认为是隔离后电压信号的AD转换值及温度传感器对应的数字量的二维函数,数据模型重构可通过对输入输出变量的离散数据集进行曲面拟合,从而得到传感器的实际负载与输入变量之间的函数关系。曲面拟合与曲线拟合的方法基本相同,目前,对传感器的数据重构最常用的方法仍然是传统最小二乘法,而传统的最小二乘法由于在整个测量区间通常采用统一的多项式模型,多项式的阶次需要试算,同时,为了避免可能出现的过拟合及欠拟合,往往采用分段拟合方法,因而其通用性在一定程度上受到限制[14-15]。移动最小二乘回归(MLSR)对传统的最小二乘回归进行了改进:①MLSR模型由系数向量及基函数构成,同时系数向量的元素为自变量坐标的函数。②引入紧支概念,自变量离散节点处的取值只受该节点附近子域内节点影响,而不受子域外的节点影响[14-17]。利用上述改进,通过在子域内选择合理的权函数,由MLSR实施对离散数据点集拟合回归可得到足够精度及光滑的曲线曲面,且相比于采用机器学习方法的数据模型重构,计算量适中,对硬件及软件资源的依赖程度降低。

应变式传感器数据重构模型建立步骤如下:

①定义在区域Θ内,存在n个数据点集{xDj,TDj}及{yj},其中xDj及TDj分别为传感器信号隔离后的AD转换值及传感器的工作温度对应的数字量,在测量区域Θ内有如下数据重构模型

(8)

式中:a(xD,TD)=[a1(xD,TD),a2(xD,TD),…,am(xD,TD)]T

p(xD,TD)=[p1(xD,TD),p2(xD,TD),…,pm(xD,TD)]T

式中:a(xD,TD)为待求系数向量,p(xDj,TDj)为基函数,m为基函数的个数

②MLSR模型中基函数通常选用一次基或二次基,基函数决定了解的基本逼近能力,一般地,选择二次基函数得到的解具有比采用一次基函数更好的逼近性能,因此选取二次基函数

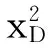
(9)

③在点集{xDj,TDj}的子域内定义式(8)的局部逼近函数

(10)

④设在数据点集{xDj,TDj}的子域内有n个数据,定义泛函

(11)

式中:ωi(xD,TD)为权函数,f(xDj,TDj)为子域内节点处的值

⑤将式(11)写成矩阵形式

J=(f-apT)Tω(f-apT)

(12)

⑥权函数ωi(xD,TD)的选择应该使得上述定义的泛函取极小值,求J对a(xD,TD)的偏导数且令其值为0,并写成矩阵形式,可得

a(xD,TD)=A-1(xD,TD)B(xD,TD)Y

(13)

B(xD,TD)=(ω1(xD,TD)p(xD1,TD1),ω2(xD,TD)p(xD2,TD2),…,ωn(xD,TD)p(xDn,TDn))

Y=(f(xD1,TD1),f(xD1,TD2),…,f(xDn,TDn))

⑦将式(13)代入式(8),可得到应变式传感器的数据重构模型

(14)

2.3 数据点集支持子域半径及权函数选择策略

在利用MLSR建立数据重构模型时,权函数ωi(xD,TD)及数据点集的支持子域半径选取对重构模型的精度影响较大,重构模型的连续及光滑与否取决于权函数,而支持子域半径决定权函数的具体表达式,因此,子域半径的选择非常重要,域半径选择过大导致模型的拟合精度降低,过小则可能导致计算量过大或得不到逆矩阵A-1。为使重构模型具有光滑及连续的特征,权函数选择三次样条函数,其选取方法具体见文献[18]。支持子域半径的选取采用域半径可变法,具体步骤如下:

步骤1 设置支持子域内的数据点个数的范围β,β为大于1的整数且不宜过大,设支持子域半径为r,选取初始半径为r0,可变系数λ为可正可负的实数且初始值为0,r=(1+λ)r0;

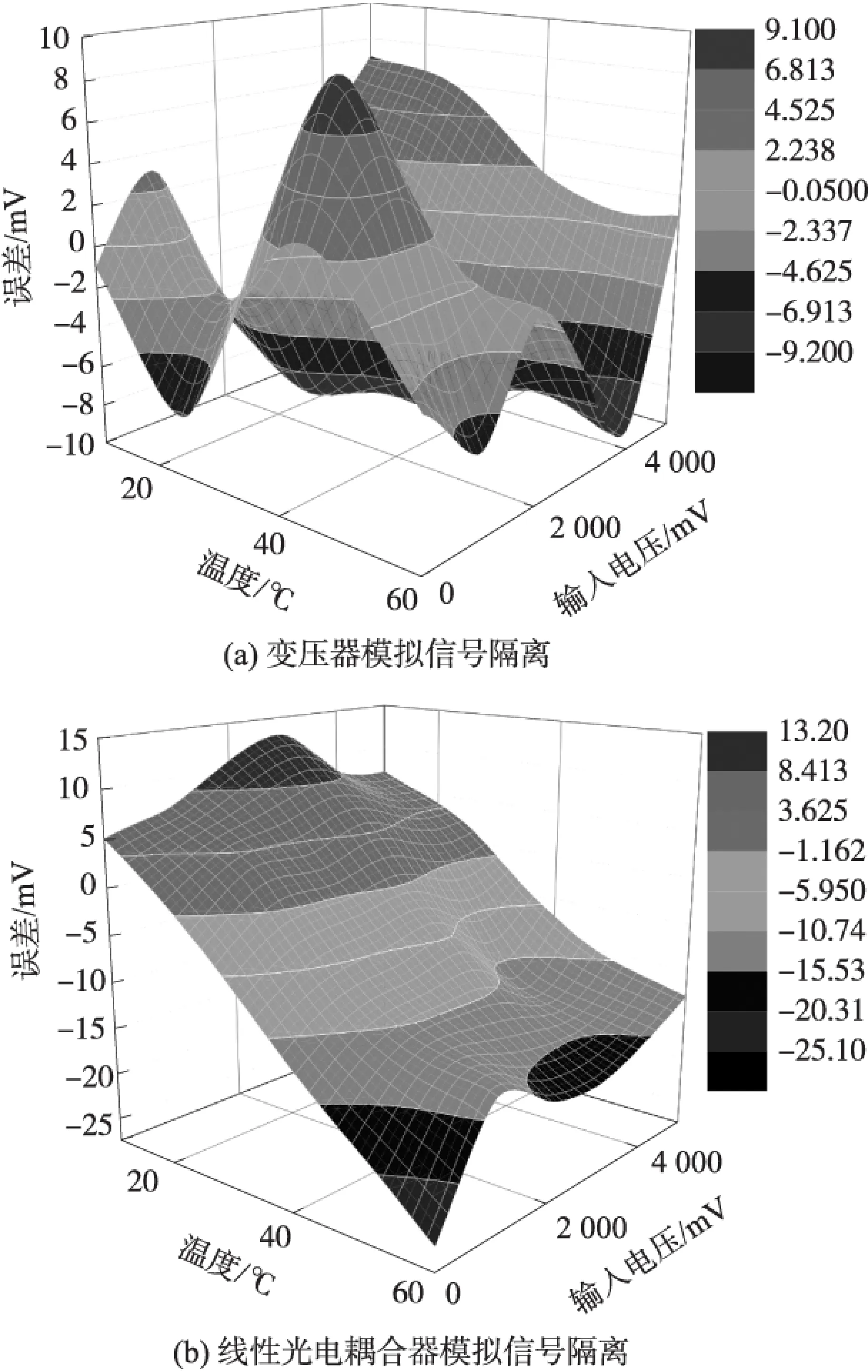
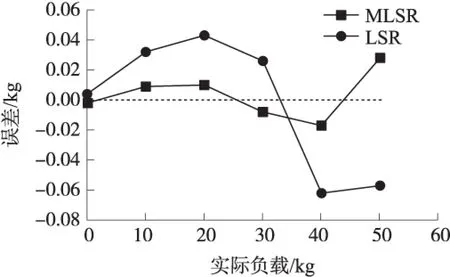
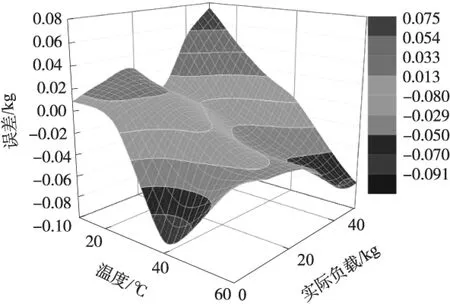
步骤2 以点{xDi,TDi}为中心,获取以域半径为r的圆内数据点集个数q,如q>β或q≤1则转入步骤3。如1

步骤3 如q>β,降低可变系数λ,如q≤1,增大可变系数λ,直至该域内的逆矩阵A-1存在为止,并选择此时的r作为该支持子域半径。

β的取值决定式(13)中矩阵A的维数,过大则增加计算量,过小则影响拟合的精度,其值需要在模型重构过程中反复测试。

3 结果分析

为验证模拟信号隔离及应变式传感器数据重构模型的效果,采用的试验装置如图9所示。分别利用本文提出的模拟信号变压器隔离电路及采用精密线性光耦HCNR201模拟信号隔离电路对隔离的效果进行对比,模拟输入信号由精密电源产生,两种隔离电路的主要器件如运算放大器等采用同批次及型号相同的精密器件。

采用MLSR及传统LSR分别对经过变压器式隔离电路隔离的应变式传感器信号进行数据重构,并对重构模型的结果进行比较。应变式传感器选用量程为50 kg的压力传感器,16位数字温度传感器ADT7310内置于应变式传感器中,选用高精度的5位智能仪表实现数据模型重构,仪表内置基于ARM Cortex-M4核的高性能MCU、24位的Σ-Δ型高精度ADC。

3.1 模拟信号隔离效果分析

模拟电压信号由图9中的精密电压源提供,将变压器式隔离电路和光电隔离电路放置于温控箱内,记录不同试验温度时隔离电路的输出,以温度为25 ℃为例,得到部分数据如表1所示。

表1 25 ℃时模拟信号隔离输出数据 单位:mV

图9 试验装置图

由表1可知,当使用温度恒定时,采用变压器式隔离电路与采用线性光电耦合隔离电路得到的模拟信号隔离精度大致相当,以满量程5 000 mV计算,变压器式隔离的相对误差为±0.16%,采用线性光电耦合隔离的相对误差为±0.12%。

改变隔离电路的使用温度,取试验温度范围为10 ℃～60 ℃,得到两种模拟信号隔离电路的误差分布如图10所示。

图10 模拟信号隔离的误差分布

由图10可知,在10 ℃～60 ℃的试验温度范围内,采用变压器模拟信号隔离电路,隔离输入与输出之间基本不受温度变化的影响,而光电隔离电路则变化较大。仍以满量程5 000 mV计算,变压器式隔离电路的隔离相对误差约为±0.2%,而采用精密线性光电耦合器的模拟信号隔离相对误差约为±0.5%,由两种隔离电路的隔离效果比较可知,采用变压器隔离电路的温度稳定性比光电隔离电路要好。

3.2 数据重构模型精度分析

虽然变压器式隔离电路具有良好的温度稳定性,但由于传感器的输入输出特性受一定的温度影响,在要求较高检测精度且传感器的使用温度变化较大的应用场合,即使传感器采用了硬件电路温度补偿,但由于其补偿效果有限,仍需要添加温度作为输入变量进行应变式传感器的数据模型重构,以便得到更高的检测精度。

试验时,将图9中的应变式传感器置于温控箱内,并给传感器施加负载,将传感器与变压器隔离电路连接,隔离变压器电路输出及温度传感器的数字信号接入5位智能仪表,改变温度箱温度,得到对应不同负载及不同试验温度时的数据点集{xDi,TDi},并由智能仪表执行数据模型重构。在试验温度为25 ℃时,得到分别采用MLSR、LSR的部分数据如表2所示及误差曲线如图11所示。

表2 25 ℃时应变式传感器模型重构结果 单位:kg

图11 温度为25 ℃时应变式传感器的重构模型误差分布

由表2及图11可知,在应变式传感器的使用温度为25 ℃时,以负载满量程50 kg计算,采用MLSR重构模型得到的负载检测相对误差低于±0.06%,采用LSR重构模型的负载检测相对误差约为±0.13%,MLSR重构模型的负载检测精度高于常规LSR重构模型。

在10 ℃～60 ℃的试验温度范围内,采用MLSR重构模型的负载检测误差分布如图12所示。

图12 MLSR重构模型误差分布

由图12可知,在10 ℃～60 ℃的试验温度范围内,采用MLSR重构模型的很好地消除了温度变化带来的负载测量误差,以负载满量程50 kg计算,在试验温度范围内,负载检测相对误差低于±0.07%,和温度为25 ℃时的检测误差大致相当。

选取25 ℃的应变式传感器的试验数据集,利用MLSR进行变压器隔离后的应变式传感器数据模型重构时,在MLSR构建的模型输入变量中不包含温度变量,此时,MLSR的应变式传感器数据重构变成了曲线拟合,即对25 ℃时传感器的试验数据集进行基于MLSR的曲线拟合得到重构模型。利用该模型计算传感器所受的负载,改变传感器的使用温度,得到的负载检测误差分布如图13所示。由图13可知,在试验温度范围内,以负载满量程50 kg计算,负载测量误差约为±0.2%,负载检测误差明显大于包含温度输入变量的数据重构模型,这主要是由于应变式传感器的输出受温度变化影响的结果。

图13 无温度输入变量时MLSR重构模型误差分布

4 结论

①研究了一种载波及解调信号为周期性方波的应变式传感器模拟信号隔离电路,利用调制及同步解调技术实现了模拟信号的变压器式隔离,该隔离电路具有较高的温度稳定性,在10 ℃～60 ℃的试验温度范围内,其隔离相对误差约±0.2%。

②利用MLSR实现对隔离后的应变式传感器信号的数据模型重构,其精度高于采用常规LSR的模型重构精度,在试验温度范围内,模型重构的满量程相对误差低于±0.07%。

③本文研究的应变式传感器模拟信号隔离及数据重构方法,同样适用于其他类型模拟信号输出的传感器应用场合,具有一定的实际使用价值。

[1] 黄桥,李忠龙,沙学军,等. 基于应变式传感器的桥梁无线测试系统的实验[J]. 同济大学学报(自然科学版),2007,35(10):1322-1325.

[2] 夏明一. 以应变式传感器为核心的人体脉搏信号采集与处理[J]. 江苏大学学报(自然科学版),2016,37(4):423-428.

[3] 马涛,马游春,张文栋. 线性光耦HCNR201在正负电压测量上的应用[J]. 微计算机信息,2007,23(2-2):297-298.

[4] 谭颖琦,范大鹏,陶溢. 基于线性光耦HCNR200的DSP采集电路[J]. 电测与仪表,2006,43(6):46-48.

[5] Analog Devices. AD210 Data-sheet[EB/OL]. www.analog.com/media/en/technical-documentation,2016.

[6] Texis Instruments. ISO122 Precision Lowest-Cost Isolation Amplifier[EB/OL]. www.ti.com,2016.

[7] 蔡欣荣,孔平. 一种采用隔离变送器模块的高精度矿井参数采集系统设计[J]. 计算机测量与控制,2014,22(12):4084-4090.

[8] Zhang Xi,Zhang Shengyan. Signal Detection Technology of Digital Closed-Loop Quartz Flex Accelerometer[J]. Infrared and Laser Engineering,2014,43(10):3356-3362.

[9] 欧阳康,洪小斌,伍剑,等. 全光纤电流互感器的新型调制解调方案研究[J]. 中国激光,2015,42(1):0105004-1-0105004-6.

[10] 王猛,肖鹏,徐林鹏,等. 差分电容硅微加速度计检测电路研究[J]. 传感技术学报,2015,28(3):347-351.

[11] 宋绍民,王敏,王耀南,等. 传感器数据的精确重构方法及其性能研究[J]. 传感技术学报,2010,23(1):52-56.

[12] 乔爱民,何博侠,张炜. 基于LS-SVM及嵌入式技术的力敏传感器温度补偿[J]. 传感技术学报,2013,26(5):637-642.

[13] 樊尚春,张秋利,秦杰. 基于样条曲线插值的压力传感器的温度补偿[J]. 北京航空航天大学学报,2006,32(6):684-686.

[14] 顾天奇,张雷,冀世军,等. 封闭离散点的曲线拟合方法[J]. 吉林大学学报(工学版),2015,45(2):437-441.

[15] 杨武,刘莉,周思达,等. 移动最小二乘法的时变结构模态参数辨识[J]. 机械工程学报,2016,52(3):79-85.

[16] Zhang Y,Lai J,Du X. Vision-Related MLS Image Deformation Using Saliency Map[C]//Image and Graphics(ICIG),2011 Sixth International Conference on USA:IEEE,2011:193-198.

[17] 李向佳,戴宁,廖文和,等. 基于MLS拟合带容差的测量数据加工刀位面生成算法[J]. 中国机械工程,2015,26(8):104-1057.

[18] 刘俊焱,云挺,周宇,等. 基于最小二乘的点云叶面拟合算法研究[J]. 西北林学院学报,2014,30(5):70-77.

乔爱民(1970-),男,副教授,主要从事数据采集系统、微机控制及其自动化、嵌入式系统、机器视觉等方面的研究,aimin_qiao@163.com;

何博侠(1972-),男,博士,副教授,硕士生导师,2009年于东南大学获得博士学位,主要从事光电测试技术、微纳米测量技术、机械动力学及先进制造技术研究。

Signal Isolation and Data Reconstruction for Stain Sensor*

QIAO Aimin1*,HE Boxia2,HUANG Yinghui1,WANG Yanchun1

(1.School of Electronic and Electrical Engineering,Bengbu University,Bengbu Anhui 233000,China;2.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

Used periodic square waves whose frequency was far higher than the sensor signal’s as the carrier signal and the synchronous demodulation one,the output of strain sensor was isolated with an isolation transformer by means of modulation and demodulation. The data reconstruction module for the strain sensor was founded by moving least square regress(MLSR). The module’s input variables included those digital signals corresponding to the isolated signal and the sensor operating temperature;meanwhile the actual load for the sensor was the module’s output variable. Experiment showed that the transformer isolation way used for analog signal isolation could get high temperature stability,and the reconstruction module had lower load detection error than the one based on traditional least square regress(LSR). Within the experiment temperature,the error of the transformer isolation for the analog signal was less than ±0.2%,and the error of load detection was less than ±0.07% by using the reconstruction module based on MLSR.

strain sensor;analog signal isolation;modulation and demodulation;data reconstruction;moving least square regression

项目来源:国家自然科学基金项目(51175267,51575281);安徽高校自然科学研究重点项目(KJ2017A565,KJ20160A452);安徽省高校优秀青年人才支持计划项目(gxyq2017098)

2016-12-22 修改日期:2017-02-16

TH823;TP212

A

1004-1699(2017)07-1062-08

C:7220

10.3969/j.issn.1004-1699.2017.07.016