线性与非线性传热过程的Cu rzon-Ah lborn热机在任意功率时的效率∗

李倩文 李莹 张荣 卢灿灿 白龙

(中国矿业大学物理学院,徐州 221116)

线性与非线性传热过程的Cu rzon-Ah lborn热机在任意功率时的效率∗

李倩文 李莹 张荣 卢灿灿 白龙†

(中国矿业大学物理学院,徐州 221116)

(2017年1月31日收到;2017年4月28日收到修改稿)

热机性能的优化是热力学领域的一个重要问题,而工质与热源之间的传热过程是热机工作时产生不可逆的主要来源.本文在引入功率增益和效率增益两个重要参数的基础上,基于一个简化的Curzon-Ahlborn热机模型并利用合比分比原理,给出了线性与非线性传热过程的热机在任意功率输出时的效率表达式,结合数值计算详细讨论了热机在任意功率输出时的特性.研究表明,参数ξ作为功率增益δP的函数存在两个分支：在第一分支上(不利情形),效率呈现出单调变化特征;在第二分支上(有利情形),效率随着的δP变化是非单调的且有最大值.随着传热指数的增加,热机的工作区域减小,这源于非线性传热过程包含热辐射所致.进一步发现功率-效率关系曲线存在权衡工作点,热机在该点附近工作能够实现最有效的热功转换.研究结果有助于深入理解具有不同传热过程热机的优化执行.

功率增益,效率增益,任意功率,效率

1 引 言

热机是将外界输入的热能转变成有用功的装置,热机效率的改进成为第一次工业革命的引擎,这是自然科学指导人类生产实践的典型范例.迄今为止,热功转换一直是热力学领域中的一个重要问题,热机性能的优化成为热力学发展的驱动力之一.当前,随着经济的全球化与社会的快速发展,能源的需求导致不可再生能源(例如：石油,煤炭等)日益枯竭,寻找可再生能源和提高热装置的热功转换效率是人类得以可持续发展的根本保证.一个不争的事实是：所有热机的工作效率的上限是卡诺效率ηC=1-TL/TH,这里TH和TL分别是高低温热源的温度.虽然基于平衡态热力学的卡诺定理是热力学第二定律的基石,但热机要想达到卡诺效率,要求其工作过程为准静态过程,这导致热机无功率输出,致使卡诺热机的实际应用受到极大的限制.众所周知,所有实际热机都是在有限时间条件下工作的,Curzon和Ahlborn[1]在1975年基于内部可逆假设提出了一个有限时间条件下的热机模型,给出了热机在最大功率输出时的效率,即CA效率但在更早些时候,Reitlinger, Yvon,Chambadal和Novikov已经做出了类似的结果,上述研究工作导致了“有限时间热力学”成为热力学的一个崭新领域[2-4].

事实上,CA效率是线性非平衡热力学框架下的热机效率的一个基本结果[5].值得注意的是,CA效率的获得是基于一个线性热转移过程,即热源和工质之间的热传导满足牛顿热传导规律.然而,实际热机在工作过程中工质和热源之间的传热过程通常是复杂的,这使得研究具有非线性传热过程热机的性能优化更加具有理论和工程实践意义.1993年,Angu lo-Brown和Paez-Hernandez[6]考虑了热源和工质之间的传热过程满足一个非线性传热定律,即Dulong-Petit定律,并详细讨论了满足非线性传热过程的热机特性.Huleihil和Andresen[7]研究了对流型传热过程对于一个内部可逆热机性能的影响,给出了该热机优化的功率和效率的近似解析公式.文献[8-11]较为系统地研究了工质与热源之间的热传递过程对于不可逆Carnot-like热机功率与效率的影响,给出了优化功率(效率)与系统参数的关系.Liang等[12]基于最小熵原则分析了多种传热过程条件下热机的热功转换特征,给出了优化热机性能的一般性方法.这些工作极大地促进了热源与工质传热过程(包括线性或非线性)如何影响热机性能的相关问题研究[13-16].

另一方面,实际的热电厂和真实热机并不是在最大功率时工作的,这主要是因为最大功率输出时热机的效率相对较小,而在比最大功率稍微小的功率工作时,热机能够获得较大的热功转换效率. W hitney[17,18]着重分析了量子器件在任意功率输出时的性能,给出了量子热机在有限功率输出时效率和功率的上限.受W hitney工作的启发,Ryabov和Holubec[19]讨论了宏观低耗散热机模型在任意功率时的优化问题,给出了最大效率和功率增益因子的关系.因此,研究任意功率(非最大功率)输出时热机性能的优化问题更具有工程实践意义[20,21].然而,热机的不可逆工作过程主要源自于热源和工作流体之间的传热过程,这种热传递过程如何影响热机在任意功率输出时的性能却很少有人关注.因此,本文系统地研究了具有线性和非线性传热过程的热机在任意功率输出条件下的性能优化问题.基于一个简化的CA热机模型并且结合代数中的等比和分比原则,解析性地推导出了任意功率输出时热机的效率与功率增益之间关系,并进一步讨论了热机性能优化与系统参数的关系,研究结果有助于人们深入理解真实热机的执行过程.

2 线性与非线性传热Curzon-Ahlborn热机和理论公式

本文所研究的CA热机及其周围环境如图1(a)所示,这里TH和TL分别是高低温热源的温度,THC和TLC分别是工质(工作流体)和高低温热源等温接触时的温度(TH＞THC＞TLC＞TL).当工质在与高低温热源等温接触过程中,其传热过程满足如下规律：

这里α为传热系数,n为传热指数.当n=1时,对应的是线性传热规律;当n=5/4时,对应的是非线性传热过程的Dulong-Petit定律.积分方程(1)和(2),可以获得工质与高低温热源接触过程中吸收和放出的热量：

图1 (a)CA热机模型;(b)简化的CA热机模型Fig.1.(a)The CA heat enginemodel;(b)a sim p lified version of the CA heat engine.

这里面th和tc分别是工质与高低温热源的接触时间.相比于两个等温过程,热机的两个绝热过程持续的时间较短,可以忽略不计,这种近似满足CA热机的内部可逆假设要求.根据热力学第二定律,两个等温过程有如下关系,

热机的功率(P)和效率(η)可以分别表示为：

为了研究热机在任意功率时的性能,我们引入了功率增益因子(δP)和效率增益因子(δη),分别表示为：

其中Pmax为热机的最大功率,ηmaxP为热机最大功率时的效率,且-1≤δP≤0.

为了优化CA热机的性能,我们定义工质与高温热源接触时,工质和热源之间的温差为x=TH-THC;工质与低温热源接触而放热时,工质与低温热源的温差为y=TLC-TL.参数(x,y)为深入研究热机的执行提供了有效途径.如果令x=y,经典的CA热机模型可以约化为一个简化的CA热机模型[22],这个简化的CA热机模型能够在优化热机性能时避免繁杂的数学计算,更为重要的是它能够较好地反映不可逆热机的工作过程,并且已被证明是一个有效的热机模型[23],简化的CA热机模型如图1(b)所示.这样 QHC=αxnth和QLC=αxntc,基于方程(5)可以得到如下公式：

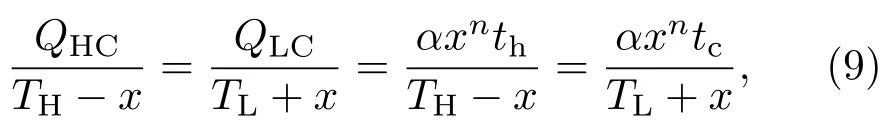
利用代数中的合比分比原理,可以得到

关于合比分比原理,可以详见附录A.利用方程(6)和(10),非线性传热热机的功率可以表示为

将功率P对变量x求导,并且满足极值条件,即d P/d x=0.这样,满足最大功率输出时

将方程(12)代入方程(11),最大功率为

将方程(12)代入方程(7)并结合方程(9),最大功率时的效率为

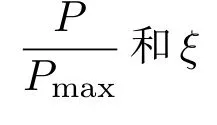
结合方程(14)和(16),任意功率时的效率可以表示为

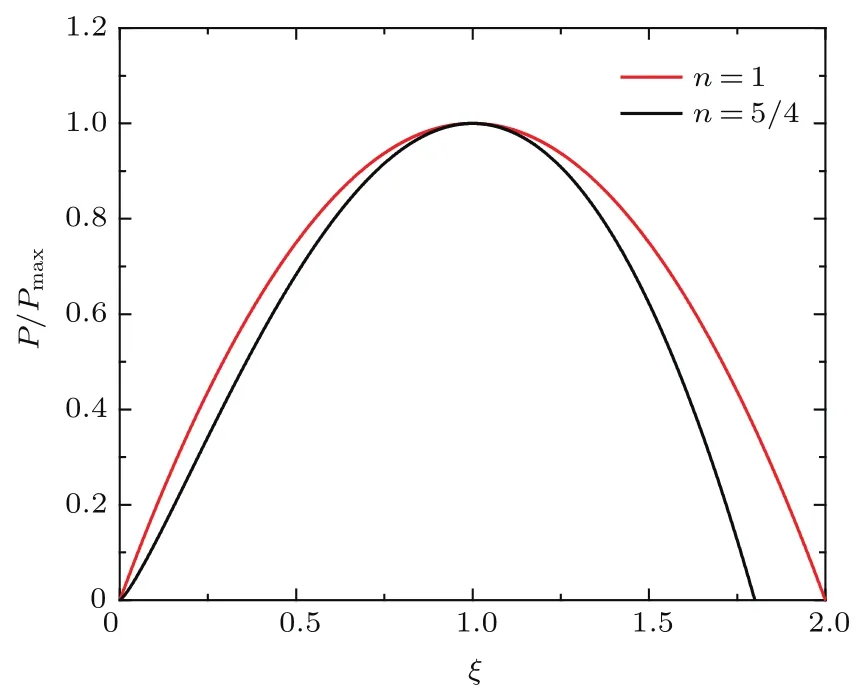
图2 (网刊彩色)P/Pmax与ξ的关系曲线Fig.2.(color online)The relation curve of P/Pmax vsξ.

理解任意功率时热机执行的关键是建立效率与功率增益的关系.基于方程(15),功率增益因子δP与ξ的关系为

当n=1时(即传热过程满足线性规律),可以得到方程(18)的2个解析解(两个分支)：

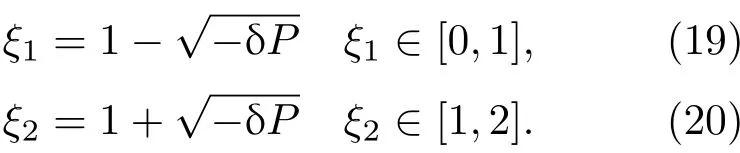
当取n=5/4(即传热过程满足非线性规律)时,解析求解(18)是非常困难的.利用数值计算,可以给出方程(18)的两个数值解(两个分支),这里假设数值解可以写为

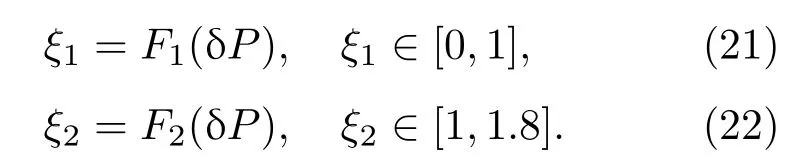
将(19)-(22)式代入(17)式,任意功率时的效率(η)与功率增益因子(δP)的关系可以被确立,这为进一步认识热机以有限功率输出时的性能提供了有力工具.

3 数值计算结果与讨论

图3 (网刊彩色).与ξ的关系曲线.Fig.3.(color on line)The relation cu rve of vsξ.

为了进一步研究任意功率输出时热机的效率,认识ξ与功率增益δP的关系是非常重要的.我们在第二部分给出了两种传热过程条件下ξ与功率增益δP的关系[见方程(19)-(22)],基于这些函数关系式,图4给出了 ξ随着δP的变化特征曲线.两种传热过程条件下ξ-δP的特征曲线均包括两个分支：热机工作在第1分支(也称不利分支)上时,当x相对于x⋆减小时,功率的减小伴随着效率的降低;热机操作在第2分支(也称有利分支)上时,当x相对于x⋆增加时,功率的增加伴随着效率的增强,甚至大于最大功率时的效率ηmaxP,参见图2和图3.非线性传热过程的ξ-δP特征曲线包含在线性传热过程的ξ-δP特征曲线之中.基于方程(17)并结合关系式(19)-(22),图5和图6分别给出了线性和非线性传热情况下热机效率η作为温度比(TL/TH)和效率增益(δP)函数的等高线图.从图5(a)和图6(a)可以看出,对于ξ取第1分支时,η随着TL/TH或者|δP|的增加单调减少;当ξ取第2分支时,η随着TL/TH增加而减小,而随着|δP|的增加先达到最大值,然后逐渐减小甚至消失.值得注意的是,虽然两种传热过程热机效率的等高曲线是相似的,但是线性传热热机工作区域大于非线性传热热机的工作区域.线性传热过程仅由热传导支配工质和热源之间的热交换,而非线性传热过程还包含热辐射过程,这导致热机工作时的不可逆程度和热损失增加.因此,热机工作在非线性传热过程时,工作区域以及效率会相应减小.

图4 (网刊彩色)ξ与δP的关系曲线Fig.4.(color on line)The relation cu rve ofξvsδP.

为了进一步阐释不同传热过程对于热机效率的影响,在固定TL/TH=0.5的情况下,图7给出了两种传热条件下任意功率时的效率η与功率增益δP的关系曲线.从图7可以看出,无论是线性或者非线性传热过程,η均是δP的双值函数,这是ξ-δP特征曲线的两分支结构在效率η与功率增益δP关系曲线中的反映.发现η-δP的曲线是闭合的“环”状结构,除了重合之处外,线性传热过程的效率大于非线性传热过程的效率,这源于较复杂的非线性传热过程引起热损耗增加所致.进一步发现,ξ第2分支(虚线)上的效率值明显大于第1分支(实线)上的效率,因为热机工作在有利分支上时,能实现更大效率的输出.另外,η随着δP变化的最大值出现在|δP|较小的值附近而不是δP=0处,即热机以比最大功率稍小的功率输出时能够获得最大效率.这意味着热机工作性能曲线存在着权衡工作点,在该点附近工作的热机能实现最有效的热功转换.从应用角度来看,这些结果为如何优化热机的执行提供了有效途径.

图5 (a)线性传热情况下效率η作为TC/TH和δP函数的等高线图,ξ取第1分支; (b)线性传热情况下效率η作为TC/TH和δP函数的等高线图,ξ取第2分支Fig.5.(a)Forξ=ξ1,the contou r-line p lot ofηas functions of TC/TH andδP with the linear heat transfer process; (b)forξ=ξ2,the contou r-line p lot ofηas functions of TC/TH andδP with the linear heat transfer process.

图6 (a)非线性传热情况下效率η作为TC/TH和δP函数的等高线图,ξ取第1分支; (b)线性传热情况下效率η作为TC/TH和δP函数的等高线图,ξ取第2分支Fig.6.(a)Forξ=ξ1,the contou r-line p lot ofηas functions of TC/TH andδP with the nonlinear heat transfer process;(b)forξ=ξ2,the contour-line p lot ofηas functions of TC/TH andδP with the nonlinear heat transfer process.

最后,根据方程(16),功率增益δη表示为

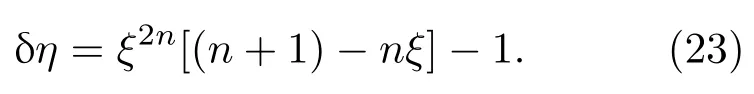
方程(19)-(22)提供了线性与非线性传热情况下ξ与功率增益δP的公式,结合(23)式与方程(19)-(22),可以获得δη-δP的关系曲线.对于线性传热过程,分别对应于ξ第1分支和第2分支的功率增益与效率增益的关系为

而对于非线性传热过程,分别对应于ξ第1分支[方程(21)]和第2分支[方程(22)]的δη-δP的关系为

基于方程(24)-(27),图8给出了功率增益δη与效率增益δP的关系曲线.从图8可以看出,两种传热情况下的 δη-δP曲线均为“环”形状的闭合曲线,在第1分支上曲线几乎重合(实黑线和实红线所示),而在第2分支上线性和非线性传热过程的δη-δP曲线略有差别(黑虚线和红虚线所示),这种微小的差异源于不同传热过程对于热机工作的影响.

图7 (网刊彩色)任意功率时的效率η与功率增益δP的关系,对应卡诺效率ηC=1-TC/TH=0.5Fig.7.(color on line)The relation curve of the efficiency at arbitrary power(η)asa function of the power gain(δP).Here,the correspond ing Carnot efficiency ηC=1-TC/TH=0.5.

图8 (网刊彩色)效率增益δη与功率增益δP的关系,对应卡诺效率ηC=1-TC/TH=0.5Fig.8.(color on line)The relation cu rve of the efficiency gain(δη)as a function of the power gain (δP).Here,the corresponding Carnot efficiencyηC= 1-TC/TH=0.5.

4 结 论

热机性能的优化对于工程实践和国民经济的可持续发展有着重要意义.实际热机在工作过程中输出最大功率时其效率并非最大,而以略小于最大功率输出时能够获得最大效率.本文基于一个简化的CA热机模型,分析了热机工作过程中不同的传热过程对于热机性能的影响.基于两个引入的参数：功率增益和效率增益,并且结合分比合比定理,给出了线性和非线性传热过程热机的最大功率、最大功率时的效率以及任意功率时效率的普遍公式.进一步发现参数ξ作为功率增益δP的函数存在2个分支.在此基础上,我们详细地给出了不同传热过程的热机在任意功率输出时的效率与系统参数的关系.发现含非线性传热过程的热机的工作区域小于线性传热过程的热机,这主要因为非线性传热过程存在着热辐射,而且随着传热指数的增加, η/ηmax的最大值略有增加且左移.任意功率时效率η作为TL/TH和δP函数的等高线图表明：对应于ξ-δP的第1分支,η随着TL/TH和|δP|增加呈现出单调减少的趋势;对应于ξ-δP的第2分支,η随着TL/TH增加而单调变化,但η随着|δP|的增加呈现出非单调特征,在TL/TH与|δP|均较小的区域存在效率最大值.非线性传热过程的热机的执行区域略有减小,这主要源于非线性传热过程的复杂性所致.两种传热过程的热机的η-δP的曲线具有闭合“环”状特征,当|δP|→0和|δP|→1时,热机的η-δP的曲线存在一定的重叠,而在其他区域,传热指数较小(线性传热过程)的热机效率大于传热指数较大(非线性传热过程)的热机效率;在热机以比最大功率稍小的功率输出工作时,可以实现最大效率的执行,这表明热机实现最佳性能工作时存在着权衡工作点.另外,两种传热过程的热机效率增益和功率增益的关系曲线也呈现出闭合“环”形状,在ξ-δP的第2分支上略有差别.本文的研究结果不仅能够帮助我们深入理解不同传热过程如何影响实际热机的性能,而且对优化受控于不同传热过程实际热机也是有价值的.

附录A 合比分比定理

在此我们对正文中用到的合比分比定理给予简要介绍.假设

这里面α/=β,β/=0,ν/=0.令方程(A 1)两边同时加上1,得到如下等式

再令方程(A 1)两边同时减去1,得到如下等式

让方程(A 3)除以方程(A 2),则

这个恒等式还可以写为

方程(A 4)就是著名的合比分比定理,在正文中推导方程(10)的过程中,我们用到了此定理.

[1]Curzon F,Ah lborn B 1975 Am.J.Phys.43 22

[2]Vaud rey A,Lanzetta F,Feid t M 2014 J.Non-Equil. Therm.39 199

[3]And resen B 2011 Angew.Chem.In t.Ed.50 2690

[4]Chen L G,Sun F R 1998 Acta Phys.Sin.18 395(in Chinese)[陈林根,孙丰瑞1998物理学报18 395]

[5]van den B roeck C 2005 Phys.Rev.Lett.95 190602

[6]Angu lo-B row n F,Phez-Hernhndez F 1993 J.App l.Phys. 74 2216

[7]Hu leihil M,And resen B 2006 J.Appl.Phys.100 014911

[8]Chen L,Sun F,W u C 1999 J.Phys.D:App l.Phys.32 99

[9]Zhou S,Chen L,Sun F,W u C 2005 App l.Energy 81 376

[10]Chen L,Li J,Sun F 2008 Appl.Energy 85 52

[11]Chen L,Sun F,W u C 2006 Appl.Energy 83 71

[12]Cheng X T,W angW H,Liang X G 2012 Chin.Sci.Bu ll. 55 2847

[13]A rias-Hernandez L A,A res de Prarga G,Angu lo-B rown F 2003 Open Sys.Inform at.Dyn.10 351

[14]Li J,Chen L,Sun F 2007 Appl.Energy 84 944

[15]Shu LW,Chen L,Sun F 2009 Sci.China Ser.B:Chem. 52 1154

[16]Chim al-Eguia J C,Barranco-Jim enez M A 2006 Open Sys.Inform at.Dyn.13 43

[17]W hitney R S 2014 Phys.Rev.Lett.112 130601

[18]W hitney R S 2015 Phys.Rev.B 91 115425

[19]Holubec V,Ryabov A 2016 J.Stat.M ech.2016 073204

[20]Long R,Liu W 2016 Phys.Rev.E 90 052114

[21]Ryabov A,Holubec V 2016 Phys.Rev.E 93 050101

[22]Agrawal D C 2009 Eur.J.Phys.30 1173

[23]Paez-Hernandz R T,Portillo-D iaz P,Ladino-Luna D 2016 J.Non-Equil.Therm.41 19

(Received 31 January 2017;revised manuscript received 28 April 2017)

Efficiency at arbitrary power for the Curzon-Ahlborn heat engine in linear and nonlinear heat transferprocesses∗

LiQian-Wen Li Ying Zhang Rong Lu Can-Can Bai Long†

(School of Physics,China University ofM ining and Technology,Xuzhou 221116,China)

The optimal performance of heat engine is an im portantissue in thermodynam ics,but the heat transfer between the working medium and two heat reservoirs induces the irreversibility during the operation of heat engine.Based on two im portant param eters introduced in this paper(nam ely,the power gain and the efficiency gain),for heat engine operating in the linear and nonlinear heat transfer processes,the formula for the efficiency at arbitrary power is achieved in terms of a simplified Curzon-Ah lborn heat enginemodel and the“componendo and dividendo”rule.The features of heat engine at arbitrary power output are also discussed in detail based on the num erical calculations.It is indicated that the parameterξas a function of the power gainδP contains two branches:the efficiency shows themonotonous variation on the first branch(the favorable case);the efficiency exhibits the non-m onotonous characteristics and has the maximum value on the second branch(the un favorable case).The working region of the heat engine is reduced as the heat transfer exponent increases,which results from the radiative contribution in the nonlinear heat transfer process. For the fi rst branch,the contour-line p lot ofηversus TL/THandδP clearly dem onstrates thatηhas the decreasing trend with increasing TL/THand|δP|;for the second branch,ηmonotonically deceases as TL/THincreases,butηshows the non-monotonic behaviors as|δP|increases.The efficiency has themaximum value in the region where TL/THand|δP| have the sm all values,and the working regim e of heat engines in the nonlinear heat transfer process is relatively sm all due to the com plexity of the nonlinear heat transfer process.The curves of the efficiency in two heat transfer processes are loop-shaped,when|δP|→ 0 and|δP|→ 1,the curves ofη～δP in two heat transfer processes are sam e.But in other regim es,the efficiency of the heat engine with the linear heat transfer process is bigger than in the nonlinear heat transfer process.Furthermore,it is found that a considerably larger efficiency can be obtained when heat engine working close to them aximum power.This im p lies that there exists the trade-off working point where the heat engine can perform the m ost effective heat-work conversion.In addition,the curves of the power gain vs.the efficiency gain also display the loop-shaped characteristics,but there is the weak difference on the second branch.Our results are very conducive to understanding the op tim al perform ance of heat engines in different heat transfer processes.

power gain,efficiency gain,arbitrary power,efficiency

PACS:05.70.Ln,05.20.-y,05.70.-a DO I:10.7498/aps.66.130502

∗中央高校基本科研业务费专项资金(批准号:2015XKM S082)资助的课题.

†通信作者.E-m ail:bailong2200@163.com

PACS:05.70.Ln,05.20.-y,05.70.-a DO I:10.7498/aps.66.130502

*Pro ject supported by the Fundam ental Research Funds for the Central Universities,China(G rant No.2015XKM S082).†

.E-m ail:bailong2200@163.com