与考研有效衔接的高等数学教学模式探索——以浙江工业大学为例

陆建芳，丁晓东

(浙江工业大学理学院，杭州 310023)

与考研有效衔接的高等数学教学模式探索
——以浙江工业大学为例

陆建芳，丁晓东

(浙江工业大学理学院，杭州 310023)

基于当前本科与考研高等数学之间在内容上、难度上、切入点上存在的差异，在《考试大纲》及历年真题知识点深度与广度的基础上，提出了一种与考研衔接的高等数学教学模式。该模式立足学校通识课程平台，整合知识要点，转变课堂教学内容的组织形式，拓展思维空间，构建考研要求的知识结构框架。针对考生在知识上、思维上存在的薄弱环节，提出相应的教学改革实践方案，并给出了高等数学两阶段教学有效衔接的措施途径,为考生提升考研水平提供了一种有益参考。

高等数学;教学改革;有效衔接;措施途径;研究生考试

随着我国高等教育的发展与普及,社会对人才需求的要求越来越高，培养高层次、综合性人才的问题日益突出。我国高校掀起了考研的热潮，主要有以下几种原因：一是一些学子立志于提高本专业的知识水平；二是社会对高层次复合型人才的需求量越来越大；三是为了缓解就业压力[1]；四是有些学子本科所学专业并非自己所愿，希望弥补高考的遗憾及实现名校的梦想；五是为了提高学历。

浙江工业大学是一所综合性的省属重点大学，现有普通全日制本科学生2万余人；2013—2017年硕士研究生招生人数分别为2038、2239、2274、2391、3127人。目前各高校都十分看重考研升学率，它是社会认可高校办学水平的一个重要指标，2012—2016年浙江工业大学升学率分别为22.21%、23.25%、21.79%、25.67%、26.33%。升学率也是学校考核学院的一个重要指标，报考成功率是学生树立信心的一个参考指标，以该校理学院统计为例，2012—2016年升学率分别为30.46%、31.92%、25.37%、35.86%、30.39%；报考成功率*成功率：指当年考上的人数/报名参加考试的人数。分别为52.6%、38.8%、50.5%、64.5%、60.0%。

从最初的考研意向到下定决心，从正式报名到答完最后一道题，这是一个艰辛而漫长的过程。在庞大的考研大军中，有相当多的学生一进入学校就有继续升造的愿望，知道目标在前方，但并不知道路在何方。引导那些基础扎实，求知欲强、积极上进的大学生,实现人生更高目标，这是学校、教师的共同责任。从学校层面上讲是尽可能地创造条件支持考研，给考生提供一个上升发展的平台，如：进行小班化教学，更有利于因材施教；开设数学建模课与数学实验课，为了将数学知识和思维方式应用于实际问题，同时也为了让学生摆脱枯噪、繁琐的数值演算；聘请专家、学长开设考研讲座，为了让考生全面了解考研过程，借鉴经验，制定合理的目标；创建考研论坛，为了让考生有交流的空间；安排考研专用教室，为了让考生有一个良好的学习环境；科学安排毕业年级的课程，为考生腾出自由支配的时间；提供相应的考研信息和复习资料，为考研做好后勤保障。

然而作为公共基础课程的高等数学，教学面临着种种问题：首先，它是为一年级新生开设的，由于受中学教育的影响，大部分新生仍然习惯于固定模式，希望授课仔细，但没有深入思考，经过大量练习，形成解题能力，从而进入了注重记忆、轻视思维的浅层次教学循环。其次，由于学习态度、学习能力、学习效果的差异，导致了分化越来越严重。再次，由于教学内容的突然增加，思维方式的大步跨越，使得一部分学生适应不了大学的学习方法，导致兴趣全无。最后，由于学时限制，使得学生只感觉学到了一些数学的基本概念、公式定理，至于数学思想、思考方式很模糊。种种原因导致数学本科教学与考研要求之间产生较大反差，这就需要通过一种教学模式来拉近差异。

围绕着数学教学的不同阶段，有着不同的衔接内容，张艳芳[2]关注高中教学大纲和高考知识点的变化。苏德矿[3]探讨了高等数学与中学数学教学方法、教学内容的差异，并给出了解决上述问题的途径。黄晓春[4]围绕着本硕两个阶段，针对应届本科推免生与研究生入学衔接阶段采取的措施。范臣君[1]根据高等数学教学现状和学生考研需求，提出了适合独立学院特点的教学改革方案。怎样更好地使得高等数学本科教学与考研要求有效衔接，需要教师仔细研究《教学大纲》与考研知识点、思维方式的差异，研究课程的教学拓展、对接研读、考研服务等，这些已逐渐成为学校展示师资力量、学风建设、提升办学水平和知名度的重要指标。

一、高等数学教学与考研要求的差异

研究生入学考试是一种选拔性考试，这种考试是为了有利于国家选拔出优秀人才继续深造攻读硕士学位的要求而设置的。数学是大多数工科、理科、经济管理类考生入学考试的必考科目，考试内容涉及到高等数学、线性代数以及概率统计三大板块。研究生入学《考试大纲》是考生备考的依据。但是目前的大学教学是以本科的《教学大纲》为依据的，自实行扩招政策后，各高校均面临着学生规模迅速扩大，生源总体差异显著加大等现象，不难理解考研要求会高于本科教学的要求，即入学《考试大纲》的要求与本科《教学大纲》存在差异，这种差异体现在高等数学上主要有以下三方面。

(一)内容上的差异

作为主干课程的高等数学是一门重要的基础学科，它对学生思维素质的培养起着重要的作用。浙江工业大学的高等数学教学内容以同济大学《高等数学》教材为依据制定教学大纲，毋庸置疑教材的编写相当出色，具备名优的特点。但由于高等教育已由精英教学转换为大众教学，使得教学要求更基础化，同时由于课时有限，使得有些知识点弱化了。考研数学将高等数学与线性代数、概率统计知识点结合在一起进行考察，考试内容已趋于完善，研究近几年的《考试大纲》(高等数学部分)及相应的研究生入学考试真卷，发现没有发生太大的变化。这与苏德矿[5]分析的题型和难度已经比较稳定的观点相一致。从卷种上来看：根据不同专业对数学的要求分为：数学一、二、三。从考试内容上来看，各专业涵盖的高等数学范围有所差异。大体上讲，数学一与同济教材基本一致，数学二、三将代数与几何、三重积分、线面积分排除在考试范围之外，数学二还删除了级数，但数学三增加了经济数学与差分方程。从局部上看，还有一些差异，如弧微分、曲率，有理(三角有理)、无理函数积分，贝努里方程、Euler方程，定积分物理应用与经济应用等在不同的数学卷种里有所取舍。从试卷结构上来看：设有选择题、填空题，主要考查考生对于基础知识的理解程度；解答题,主要考查考生计算能力和数学方法的掌握程度。从试卷分值上来看：高等数学部分，数学一占60%，数学二占80%，而数学三占50%，且各卷种侧重点相差很多。

(二)难度上的差异

《教学大纲》要求学生初步了解高等数学的理论体系、思维方式和研究方法，因此在教学设计时，往往选择知识点相对较少、独立性较普遍、综合性较弱的例题进行讲解、练习、考试。而考研数学扩大了考察的知识面,综合性更强、技巧性更高、相关性更多。对于本科教学，由于学时限制，泰勒公式、变限函数、含参函数等一带而过的知识点，频繁地出现在历年的考研真题中，这亟需加强。《考试大纲》不仅要求考生具备数学基础知识的功底，还对考生提出了更高的要求。要求考生比较系统地理解数学的基本概念，掌握数学的基本方法；需要“联网”，具有广泛联想、发散思维、逆向思维；在综合应用、考试技巧等方面加强训练；不仅要掌握解题思路，还要保证计算速度与精度。

(三)切入点的差异

《教学大纲》要求按照教材的目录次序按部就班组织教学。查阅相关资料，考研复习可以分为以下几个阶段。基础阶段：要求考生比较系统地掌握数学的基本概念、基本理论和基本方法。强化阶段：针对真卷中常考的题型进行大量的联系，搭建考研数学结构框架；要求考生在抽象思维能力、逻辑推理能力、空间想象能力、科学运算能力和综合运用能力等方面有所突破。冲刺阶段：通过练习真题来揣摩命题者的出题思路与规律，从而增加复习备考的针对性和有效性。模拟阶段：通过模拟，身临其境地感受考场的氛围，从而不慌不忙地成功应付考研来组织复习。

如何正确处理和化解高等数学本科教学和考研要求之间存在的差异，是本文讨论的重点。

二、与考研有效衔接的高等数学教学模式

为了缩小《教学大纲》与《考试大纲》(高等数学部分)要求之间的差距，探索一种新的教学模式已成必然。基本思路是在本科高等数学基础上，通过纵向延伸、横向扩展、系统思维、章节串联等形式，改革教学过程，建立一个更完善的适应考研要求的知识体系；充实和加强考研所需的高等数学知识，系统总结考研基础、热点、难点，强化基本训练和计算技巧，解决本科与考研高等数学两个阶段扣合与断层衔接问题，使考生能够循序渐进，逐步地从基础知识的巩固过渡到有针对性的全面复习阶段，这是值得教育工作者们关注的问题，对断层中知识的补充以及怎样处理思维的跨度成为一个现实问题。

大学之道不唯在传授知识，更在于构建学生良好的认知结构和认知方式。按美国心理学家奥苏伯尔的观点，良好的认知结构：在纵向上自上而下逐渐分化，在横向上融会贯通。因此本文在原有高等数学的知识结构基础上，设计了衔接教学模式流程，如图1所示。

图1 衔接教学模式流程

实现衔接教学目标需要借助一定的教学形式，本文选择最基本的课堂教学形式来组织衔接教学。

三、高等数学衔接教学的实践措施

(一)衔接教学模式的实践内容

本科与考研衔接教学，是一项艰巨的工作，需要教师熟悉当前高等数学本科教学的现状及存在的问题；花时间、精力去深入研究考研要求的内涵与外延。根据教学设计的理念[6]，本文构建了课程教学设计的构架，完善、调整教学内容和编排体系。在新的框架下，通过学校通识课程平台，根据学校教学周时间安排，将高等数学考研内容整合成若干个专题；每个专题按解决问题的途径，分成若干种方法；每个方法强调若干个要点：精心设计出每堂课教学内容的结构。围绕着结构，做好备课这项永无止境的再“创作”工程；授课时，简要回顾准备工作，引入定义、定理条件，展开定理内容，分析定理结论，归纳用在何处、思考如何用。按《考试大纲》的要求，讲透高等数学定义、定理、公式的表层概念，同时还应将数学的思想、思维的方式、解题的方法渗透到例题这个知识的载体中去。将高等数学的知识点串在一棵“倒长”树上；将思维方式联通相应的知识点；将知识之树从无到有，从上到下，从模糊到清晰，逐渐细化、充实、链接。让考生知道知识点从哪里来，到哪里去，其中的关系怎么样，路径又怎么走。在有理念、有目标的引导下，有方法、有步骤地开展教学活动。把“教”从知识传授为主逐步转向以导为主，把“学”从模仿为主逐步转向以探究为主的实践模式[6]，探索如何实现紧凑有效的过渡,把学生引入一个完整的高等数学考研领域，使得教学材料层次化，题材内容合乎化，解题思路程序化，教学活动主题化，这是任课教师面临的、亟待解决的教改课题。同时采取多种形式的课外辅助方法：利用课后15分钟，解答课堂上的疑难问题；通过课后作业，加强热点问题的研讨；借助微信等通讯工具，共享考生复习时碰到问题的解决方法；充分利用图书馆资源，鼓励考生将专题中的方法、要点查阅补齐。

(二)衔接教学模式的实践措施

高等数学教育层面的改革研究很多，如张霞等[7]从学校层面上提出教学改革思路及取得的成效；陆志雯[8]从多个视角给出了对“高等数学”教学内容的合理处理以达到提升课程教学质量的目的。但本科与考研高等数学衔接教学层面的教改措施和方案却很少。关于“教什么”和“怎么教”，它是教师根据高等数学的原理和考研要求，运用系统的方法，对参与教学活动的诸多因素所进行的一种行之有效的分析和策划[6]，考研知识信息分析、教学内容凝练、教学环节设计、教学方法改进、思维方式拓展等核心问题的改进,关键是找准突破口，通过以下途径来实践。

1.强调三基基础上突出热点问题

考研数学70%的题是考察三个基本，即基本概念、基本定理、基本方法。因为基础知识是学习支撑体系的最小元素，对基础知识的考察要求教学内容既要全面覆盖，又有所侧重，同时还要突出要点，注意层次。考试失分的一个重要原因就是对基本概念理解不准确，某些概念用什么术语来叙述容易搞混，导致解题不得要领。所以在考研衔接教学授课时，在回顾已有知识的基础上，对概念、要点讲解要达到一定的比例与必要的深度。如极限理论里主要考核求极限的方法，但方法是建立在概念基础上的。求极限limf(x)=A，(包括无穷小、无穷大等)共有30个概念。讲解时首先教会学生极限概念的辩证思维，即由静止到动态，从精确到无限接近，从有限到无穷转变的过程；其次，对涉及的四个量ε,δ;M,X(N)之间的关系高度凝练；再次，总结什么概念用什么方式符合表述。在此基础上归纳求极限的各种公式、各类方法及注意事项；进而要明确“热点”问题——未定型极限。只有这样才能对碰到的问题进行归类、解答。

2.公式与图形相联系的形象化记忆

公式是一个庞大的群体，公式的记忆是学好高等数学必不可少的环节，记不住的东西，是永远不会用的，看到公式就头大的学生会产生畏惧心理，更是谈不上兴趣。考试失分的一个重要原因就是对基本定理、公式记不牢、记不全。因此在讲解时将公式和几何图示形象地结合，将复杂的公式变成看得见、握得着、记得牢的模型。如“多元复合函数偏导数”的链式法则，由于运算复杂，考生很容易“漏掉”一部分尾巴。为了掌握其规律，讲解时可以和相应的函数复合结构图相联系，强调复合函数的分解，通过“路相加，步相乘”的方式记忆，并加以推广到各种各样求导问题。通过数形结合的过程实现抽象公式与形象表现之间的转化。

3.教学内容的高度凝练

考研数学命题范围有明确的规范，但命题的形式千变万化。在详细研究考试的基本要求，题型、类别、难度和特点的基础上，准确定位。如考研试题中，对变限函数及含参函数这类问题要求比较高，可以专门开设一次专题，从函数的角度，把变限函数及含参函数的求值、表达式、极限、导数、微分、单调、极值、凹凸、拐点、积分等问题，通过变形高度凝练为变限函数导数计算来解决。对考纲中每个知识点定位讲解后，把知识联系起来。因为考研很少单独考核某个知识点，而是综合考察考生的分析能力和解题能力。所以凝练内容，可以使得千变万化的知识点凝练成几类问题，使得理解、记忆简单化。

4.重视计算能力

计算能力可以说是考研的第一能力，考研数学考试的计算，不是考察简单的数字计算，而是考察概念和算理的一个过程。考生计算问题上的共性，一是计算能力弱，二是没有找到好的计算方法，导致算得慢、做得繁。因此在教学过程中，要考生克服满足于知晓运算过程、眼高手低的坏习惯，平时应真正动手进行计算。同时总结一些运算技巧，如积分运算中的奇偶性技巧。要求考生明确每步计算的根据是什么，做题时不要跳跃，这样既能巩固已学的知识点，又能在实践中提高计算能力。

5.突出数学的应用价值

应用性是数学的特点，解答应用题是分析问题和解决问题能力的高层次体现，反映出考生的综合意识和实践能力。应用题在真题中频繁出现，考试失分的主要原因是具体问题提炼不出数学模型，所以讲解时应有所体现。应用无非涉及几何、物理与日常问题，数三的应用题更会涉及经济问题，因此要补习相应的概念及经济数学知识点。将建模的思想渗透到课堂的教学中，从多种途径概括出数学模型，让考生从建模过程中真正体会到数学是因为有用而产生的，体会到数学的应用价值。

6.更加注重问题的本质

7.抓住规律，举一反三

考研真题中经常会遇到多、繁、杂等题型，这时就要想方设法将“多”化“少”、将“繁”化“简”、将“杂”化“规”，从中抓住规律。在教学过程中，引导考生不断反省，对的问题要思考，错的问题要总结，争取做到做一道题会一类题。教会学生举一反三、触类旁通，要从题海战术种跳出，进行技术性的辅导、练习。拓展学生的思维空间，使教学过程成为学生积极探究的过程。

8.梳理概念，理顺主次关系

在组织教学时，要依据《考试大纲》将考点的内容重新梳理，理出主干。对于重点内容要反复强调，对于难点问题要有所突破，对于关键步骤要充分紧抓。即使是同一个知识点，数学一、二和三在考察的角度和方式上还是有所变化的。数学一和数学二侧重于原理与方法的探究；数学三更侧重于计算，而对于原理的深度不做过高要求。因此，在不同的目标要求下，构建有层次性的课程体系；对某些内容加强、对某些内容适当降低要求。教师应该密切关注各专业考研数学的出题趋势，梳理课程教学的核心知识，使教学内容、方式尽可能跟上考研的步伐。

9.处理变式问题，把知识融会贯通

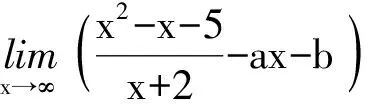
10.理清脉络，不重不漏构建结构体系

在明确每堂课的知识目标、能力目标前提下，打破传统教学模式，将每一个知识点与相关的真题、模拟题重新整合。课堂教学分16个专题，首先对每个专题知识、要点进行精讲，随后提供相应试题实战、接着进行重点、难点解析及分析，最后进行整体总结，点评涉及哪些知识点，可能会出错的地方。这样使每一个知识点串联成线，挂在“倒长”的知识之树上，最后连接成面，深度掌握。当高等数学提高课程讲授完毕，在考生的脑海中留下的是“倒长的知识框架之树”。

四、衔接教学模式实践成效与面临的问题

作为高等数学衔接教学模式探索，笔者从2014年暑假开始，选择了一个学院开设这种模式教学实践。2015年初试考研上线率*注：初试考研上线率，即当年初试上线人数/本科毕业人数。为10.23%，比2014年增长了近8个百分点，报考人数增长了3倍，首创佳绩。2016年初试考研上线率为12.4%。2017年初试考研上线率达17.7%。一年一个台阶，稳步上升，这证明该教学模式有可取之处。2017年开始在浙江工业大学全校范围内开设高等数学衔接教学模式的通识课程，希望全校考研升学率由5年前的22.21%螺旋式提高到26.33%，转变成直线突破，目标锁定在35%左右。

这是一个庞大的工程，不是短时间就能够解决的。但是，只要朝着既定的目标不懈努力，考研数学课程的教学就一定会越来越有利于为优秀有志青年的培养创造良好的平台，取得教学改革成效。笔者将衔接教学目标定位在：数学基础较差，经过衔接教学，争取考研成绩过线，能够顺利地跨入硕士研究生的大门；数学基础较好，争取高分，增加一份被更高级平台录取的机会。

作为一种尝试，衔接教学不可避免地遇到了一些问题。首先，衔接教学模式在全校范围内铺开仅仅刚开始，考研数学的教学改革有待进一步规范，线性代数与概率统计相应的衔接有待准备；精心组建教师团队，是实现考研辅导的根本保障。其次，这种教学模式还需教育体制的支持，虽然得到了校、院的认可，在通识平台上运行，但它仅仅作为拓展视野教学，暂时还未正式纳入本科必修教学计划。再次，衔接教学课时欠缺，得不到足够的保障，还需要适当增加选修课时。最后，由于数学一、二、三对高等数学、线性代数、概率统计深广度要求的差异，最好进行分层针对性教学。构建并逐步完善符合各高校高素质人才培养目标的大学教学创新体系。

五、结 语

培养合格的大学生，向更高层次的培养单位输送更多的硕士研究生是各本科院校的职责。从教学层面上讲，它需要教师实时关注《考试大纲》要求的变化，研究本科教学的基础现状与考研要求的深广度，准确地把握学生已有的数学基础水平与缺失的知识，从而采取有效的措施做好教学的衔接工作，帮助考生从本科高等数学水平跨上考研平台。为了实现我们期望的成效，在教学中，要根据考生的需求，以考生为中心，以考纲为目标，发挥教师的使命感，不断跟踪考研数学深度与广度的大势，不断探寻各种行之有效的教学方法，不断弥补各位考生的数学知识、思维的缺损。把改革措施落实到实处，整合教学内容，突出有效性，提高数学视野，扩展思维方式，以贴近不同学科专业的考生对高等数学知识的实际需求为宗旨进行改革，提升考研的升学率。

[1] 范臣君.基于考研需求的独立学院高等数学教学改革[J].价值工程，2007(7):224-225.

[2] 张艳芳.大学高等数学课程和新课标下高中数学的断层与衔接研究[J].大学教育，2016(5):108-110.

[3] 苏德矿.高等数学教学如何与中学数学内容及教学方法有效地衔接[J].中国大学教学,2013(5):47-49.

[4] 黄晓春.本硕衔接教育研究与探索[J].中国大学教学，2011(2):36-38.

[5] 苏德矿.从考研数学阅卷来分析考生的学习质量及应对策略[J].大学数学，2014，30(5):87-91.

[6] 赖绍聪.如何做好课程教学设计[J].中国大学教学，2016(10):14-18.

[7] 张霞.地方应用型本科高校高等数学课程教学改革的研究与实践[J].中国大学教学,2009(8):29-30.

[8] 陆志雯.“高等数学”教学中如何处理教材内容[J].上海理工大学学报(社会科学版)，2016:38(3):281-285.

(责任编辑： 康 锋)

Research of Teaching Mode of Higher Mathematics Specific to Postgraduate Entrance Examination: Case Study of Zhejiang University of Technology

LUJianfang，DINGXiaodong

(School of Sciences, Zhejiang University of Technology， Hangzhou 310023， China)

Considering the differences between Higher Mathematics for undergraduates and that for postgraduate entrance examination in content, difficulty and focus, a teaching mode of Higher Mathematics specific to postgraduate entrance examination is put forward based on the depth and range of the examination syllabus and the knowledge points in the examinations in the past years. This mode is to be realized by integrating main points of knowledge, transforming the organizational form of classroom teaching contents, expanding thinking space and establishing a knowledge structure framework meeting the requirements of postgraduate entrance examination based on general education curricula. To help students overcome the weakness in knowledge and thinking, a teaching reform practice plan is put forward, and measures for linking up higher mathematics teaching in the two stages are presented, which provides a reference to students for getting improved in postgraduate entrance examination.

higher mathematics； teaching reform； effective connection； measures； postgraduate entrance examination

10.3969/j.issn.1673-3851.2017.08.013

2017-05-05 网络出版日期： 2017-07-20

浙江工业大学教学改革项目(GZ16401090034)

陆建芳(1964—)，女，浙江湖州人，副教授，主要从事高等数学基础教育方面的研究。

G423

A

1673- 3851 (2017) 04- 0365- 06