捷联式重力仪在海洋测量中的应用与数据处理

罗 骋，薛正兵，李东明，李海兵，王文晶，马存尊

(北京航天控制仪器研究所，北京100039)



捷联式重力仪在海洋测量中的应用与数据处理

罗 骋，薛正兵，李东明，李海兵，王文晶，马存尊

(北京航天控制仪器研究所，北京100039)

针对海洋重力测量对重力测量系统的要求，给出了一种捷联式海洋重力仪SAG-2M，论述了系统组成、工作原理、特点和数据处理流程。利用近期获得的某海域重力测量数据，评估了捷联式重力仪精度。测量结果表明，重复测线的重力异常曲线吻合度较高，交叉点不符值精度约为1.2mGal，满足海洋重力测量的指标要求。

捷联惯性导航系统;GPS;SAG-2M;重力异常

0 引言

海洋重力场是地球重力场的重要组成部分，也是海战场环境的重要组成部分。海洋重力场信息在海洋资源勘探、地球科学研究、海战场环境建设、水下导航等经济及国防领域具有非常重要的价值和作用[1]。高精度的海洋重力场信息是研究海洋地质构造、资源分布、查明地质体存储状态必不可少的基础数据[2-3]。同时，对航天飞行器的精确定轨、精确制导和水下匹配导航等起着至关重要的支撑作用[4]。

海洋重力场的测量是在陆地重力测量基础上发展起来的，从海洋重力测量的发展历史看，人们采用过的海洋重力测量手段包括海底重力测量、海面船载重力测量、海洋航空重力测量和卫星测高重力测量等。卫星测高重力测量技术的出现极大地改善了海洋地区的重力测量状况，填补了大量的重力测量海洋空白区域，极大地丰富了人们对于地球重力场的认识。利用卫星测高数据计算海洋重力异常已成为了目前获取全球海洋地区重力场信息的主要手段，研究结果表明，采用测高资料反求重力异常，在30′× 30′范围内，平均重力异常精度可达3.5mGal，已达到较好的精度水平[1]。但受限于卫星高度，只能测定地球重力场的中长波分量，对于海洋重力场的中低频信息，虽然能通过测高信息反演，但仍与船载重力测量和航空重力测量方式有一定的差距，近水区域尤为明显。因此，在现有技术条件下，获取高精度、高频的海洋重力场测量信息的主要方式仍是海洋重力测量和航空重力测量。

目前，我国只有不到一半的陆地国土完成了1∶20万的重力测量，另有不到一半的国土面积完成了1∶50万和1∶100万的重力测量。在海洋区域，仅初步完成了覆盖第一岛链海区的海洋重力场精密测量。随着“一带一路”、海洋强国战略的推出，国家对海洋的开发和利用步伐明显加快，势必对海洋重力测量仪器产生较大需求，开展船载海洋重力测量和航空重力测量技术研究对于国民经济和国防事业有着重要意义。

在这样的背景下，本文给出了一种基于捷联惯性技术的海洋重力仪SAG-2M。

1 捷联式重力仪的测量原理

1.1 原理概述

捷联式重力仪的测量原理是，安装在船舶等载体上，在线连续测量载体系上的比力(保守力及非保守力之和)信息及载体角运动信息，离线事后处理获得载体途径地标量重力信息的精密测量仪器。

载体系上的比力信息由加速度计测量，载体角运动信息由陀螺仪测量，在指北系或游移系的力学编排下，经过数学平台可以计算出载体相对于当地地理坐标系的姿态，比力信息通过姿态投影计算获得垂直方向分量，再与PPP(或差分GPS)估计出的载体垂向运动加速度求差，经过特定的滤波估计，最后得到航迹上的标量重力信息。

1.2 捷联式重力仪重力测量数学模型

捷联式重力仪重力测量数学模型是基于惯导系统的比力方程推导出来的，惯导系统中的比力方程为

(1)

(2)

式中，fU为天向比力，L是载体所在地纬度，h为高度，vE和vN分别为载体的东向和北向速度，式(2)中的重力加速度值可以表示为正常重力值与扰动重力之和，则有[5-7]

(3)

式中，γ为正常重力值。式(3)即为重力异常测量的基本模型，记

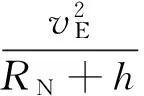
(4)

则海洋重力异常的计算公式变为

(5)

其中，第一项fU的精度取决于惯导姿态与加表的测量精度；第二项为厄特弗斯改正，计算公式如式(4)所示；第三项为天向运动加速度改正，在海洋重力测量中，由于海浪引起船在高度上的短周期变化可以通过数字低通滤波器处理予以消除，因此在海洋重力测量中可不考虑该误差项；第四项为正常重力改正，与载体所在纬度和高度有关，有

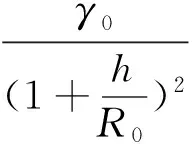
(6)

式中，h为测量时刻载体的海拔高；R0为地球平均半径，有

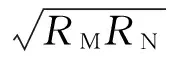
(7)

式中，RM和RN分别参考椭球点的子午圈半径和卯酉圈半径，计算公式如下

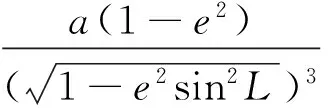
(8)

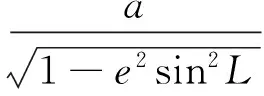
(9)

式中，a为椭球的长半轴，f为椭球扁率。

式(5)中，第二至第四项可以通过GPS提供的速度和位置信息进行计算。目前， GPS技术已经较为成熟，其定位和速度精度较高，能满足重力测量对GPS的精度需求。因此，重力异常的提取精度取决于天向比力fU的精度，即比力fn的天向分量，有[8]

(10)

SAG-2M海洋重力仪中的陀螺和加速度计的随机误差会随着时间而漂移，进而影响系统的姿态角精度和比力测量精度。为了获取高精度的重力异常信息，需要考虑器件误差对系统结果造成的影响，因此采用组合导航的方式修正惯性器件漂移引起的姿态误差，具体流程如图1所示。

图1中，卡尔曼滤波器所用的惯导系统误差状态方程可表示为

(11)

考虑到滤波器计算量，所用的状态向量可以适当简化，取系统状态向量

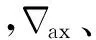
Z=HX+V

(12)

根据图1所示流程，数据处理可按如下步骤进行：

1)根据惯性器件测量的载体当前时刻的角速度和加速度计算载体当前时刻姿态、速度和位置信息；

2)利用GPS提供的载体速度和位置信息，并根据式(11)和式(12)估计惯导姿态角误差，得到载体姿态误差角；

3)修正姿态阵，根据式(10)重新将比力投影至地理坐标系得到修正后的比力；

4)根据GPS信息提供的速度及位置信息，按式(4)～式(9)计算载体的厄特弗斯改正以及正常重力值；

5)根据噪声特性，设计低通滤波器消除测量噪声，得到高精度的重力异常信号。

2 SAG-2M系统简介

国际上，已有两种类型的航空标量重力仪得到了较好的商业应用。第一类为基于阻尼二轴平台式重力仪，以Chekan-AM、LRS、BGM-3为代表[9-12]。第二类为基于三轴惯性稳定平台重力仪，以GT-1A、GT-2A、GT-2M和AIRGrav为代表[13-17]。两类重力仪均可获得1mGal的测量精度，可满足地质调查和资源勘查的需求。此外，还有第三种方案，将SINS安装在载体上，与DGPS一起构成另一种动基座重力仪， 1995—1998年加拿大卡尔加里大学验证了基于SINS/DGPS的重力仪方案的可行性，自此基于SINS/DGPS的重力测量系统成为了业界的研究热点[18-22]，该系统以航空惯导为基础，测量精度为2～3mGal。

相比于传统的平台式重力仪，基于SINS/DGPS的捷联式重力仪具有以下特点：

1)重力传感器输入范围宽，动态特性好，同时具有稳定的线性漂移率，可以进行有效的数学补偿；

2)陀螺为全固态光学惯性器件，相对于机械式陀螺，可靠性大幅提升，同时具有良好的动态环境适应性，降低了对搭载平台的条件要求；

3)捷联式重力仪具有更高的可靠性和方便维护的优点；

4)系统质量小、体积小、功耗低，可以考虑冗余配置，形成热备份，增强测量作业系统可靠性。

SAG-2M海洋重力仪采用的是SINS/GPS系统方案，其构成如图2所示。

SAG-2M海洋重力仪包括重力测量单元与显控单元共同组成动基座重力测量系统(见图3)。其中，显控单元有记录仪、不间断电源UPS、供电开关控制及电流显示盒。

在形成商业化产品的过程中，考虑到海洋测量应用环境长航时、高可靠性的要求，对原有系统进行了一些适应性改进设计，主要包括：

1)由于系统精度与重力传感器精度直接相关，因此针对海洋测量应用环境，对SAG-2M中的重力传感器进行了适应性改进。

2)一次重力测量作业可能长达几个月的时间，这对重力传感器的长期稳定性提出了极高的要求。通过选取关键部件的材料、改进磁路设计、优化工艺等措施，提高参数的长期稳定性，使重力传感器达到预期指标要求。

3)海洋重力测量对减振器提出了特殊的要求。在原有一级减振的基础上，重新设计了减振系统，采用多级减振的方案，使其具有宽频带的减振性能，以削弱发动机等引起的高频扰动加速度的影响，保证重力作业全程的动态需求。

4)海洋重力仪应在0℃～40℃的环境温度条件下均能正常工作。为此，对温控系统进行特别设计，使温控精度可达0.01℃，保证仪器内部的恒温条件，确保了不同环境温度下的重力作业测量精度。

5)考虑到产品美观的需求，将除UPS电源单元外的其他部分集成为一个整体，提高了产品的集成度，SAG-2M产品外观如图4所示，主要技术指标如表1所示

指标名称指标要求动态范围±2.0g量程20,000mGal零点漂移率(标校后)<4.5mGal/月最大倾角1)横摇2)纵倾 ±45°±45°纬度测量范围75°S～75°N工作环境温度+0℃～+40℃重力测量作业推荐工作环境温度+18℃～+28℃工作海况<6级静态测量精度<0.4mGal海上测量精度优于1.5mGal系统准备时间1)冷启动2)待机模式 48h4h

3 SAG-2M在海洋测量中的精度评估与测量结果

为评价SAG-2M海洋重力仪的动态性能，在产品研制过程中，对SAG-2M海洋重力仪进行了充分的海洋重力测量试验验证。下面简要给出海洋重力测量的精度评估方法和某航次海洋重力测量试验结果。

3.1 海洋重力测量的精度评估方法

海洋重力测量后，按图1所示流程处理海洋重力测量数据，在取得数据结果及航迹上各个测点的重力异常后，需要对整个航次的测量数据进行精度评估。海洋重力测量精度评估方法与陆地类似，大致分为内部精度检核和外部精度检核。对于海洋重力测量来讲，内部精度检核指的是在若干测线上，重复测定一些测点，根据重复测点的符合程度来评估整个测区的测量精度；外部精度检核指的是使用具有较高精度的海底重力仪测量成果，来检查海面重力测量在一些重复点上的符合程度。

在海洋重力测量过程中，海底重力测量成果较难获得，且船载的航行区域多为深远海，难以在海底布设重力仪获得基准数据。因此多采用内部精度检核的方式评估仪器的测量精度。

由于海洋测量环境的特殊性，使得测量时无法在更多的观测点上进行重复性测量，只能依靠2个交叉点获得重复观测值。因此，海洋重力测量的精度评估是一种带有抽样性质的近似评估方法。

假设在某海域重力测量形成若干交叉点，则可以根据式(13)评估本区域的测量精度。

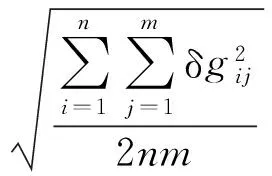
(13)

式中，δgij=δg1-δg2表示交叉点的重力不符值，δg1和δg2分别为第一次和第二次通过交叉点时的重力异常测量值；n和m分别代表主副测线的数目总数。考虑到某些主副测线可能不存在交叉点，精度评估的实用形式为

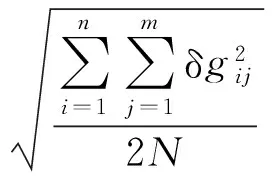
(14)

式中，N代表主副测线的实际交叉点个数。

3.2 SAG-2M海洋重力测量试验结果

SAG-2M某航次搭载测量航迹如图5所示。

该区域的载体姿态如图6所示，可以看出，SAG-2M在该海域进行海洋重力测量时，外部环境较为恶劣，船体受海况影响，晃动幅度较大，横摇角可达18°。对整个航次的数据进行事后处理，获取整个航次的重力异常信息。

在进行交叉点计算内符合精度之前，先截取航迹上的东西向、南北向重复测线各一条，以检查SAG-2M在该航次测量中的系统误差。如果存在系统误差，则进行重复测线测量时，所得到的重力异常曲线会出现常值偏离。

(1)东西向重复测线

从图7中可知，东西向测线中的蓝色和绿色曲线为东西向重复测线，横轴为经度，纵轴为纬度；图7中各测线测得的重力异常曲线如图8所示。

(2)南北向重复测线

图9中，南北向测线中的蓝色和绿色曲线为重复测线，横轴为经度，纵轴为纬度；图9中各测线测得的重力异常曲线如图10所示。

从图8和图10的对比结果可知，SAG-2M在进行东西和南北向的重复测线测量时，测量得到的重力异常曲线的吻合度较好，说明SAG-2M海洋重力仪的系统误差控制较好。

由该航次的航迹信息可知，在该区域内存在30个交叉点，如图11中的红色标记所示。

对上述30个交叉点的不符值进行计算，结果如图12所示。采用式(14)统计30个交叉点不符值的中误差，结果约为1.2mGal。

此次试验表明，SAG-2M海洋重力仪能在海况较为恶劣条件下正常工作，环境适应性较好。重复测线重力异常曲线吻合度较高，系统误差小；30个交叉点测量精度约为1.2mGal，达到了仪器预期的设计精度，也达到了国外成熟重力仪产品的精度水平，能够满足海洋重力测量精度需求。

4 结论

在国家推行“一带一路”、海洋强国战略背景下，国家对海洋的开发和利用步伐明显加快，对海洋重力测量仪器产生较大需求。北京航天控制仪器研究所采用了SINS/DGPS捷联式重力仪研制方案，针对海洋重力测量的应用环境，进行了大量改进，并成功研制出SAG-2M捷联式海洋重力仪。

在研制的过程中，对SAG-2M进行了充分的海洋重力测量试验验证，重复测线的重力异常曲线具有较好的重复性，交叉点测量精度约为1.2mGal，达到了国外成熟产品的精度水平，具备实施海洋重力测量的能力。

[1] 黄谟涛，翟国君，管铮，等.海洋重力场测定及其应用[M].北京：测绘出版社，2005.

[2] 宁津生，刘经南，陈俊勇，等.现代大地测量理论与技术[M].武汉：武汉大学出版社，2006.

[3] 黄谟涛，翟国君，欧阳永忠，等.海洋磁场重力场信息军事应用研究现状与展望[J].海洋测绘，2011,31(1)：71-76.

[4] 宁津生，黄谟涛，欧阳永忠，等.海空重力测量技术进展[J].海洋测绘，2014，34(3)：67-72.

[5] 欧阳永忠.海空重力测量数据处理关键技术研究[D].武汉：武汉大学，2013.

[6] 熊志明，郭刚，李东明，等.基于正反Kalman滤波的动基座重力仪数据处理方法[J].导航与控制，2017,16(1): 74-80.

[7] 李东明，郭刚，薛正兵，等.激光捷联惯导车载重力测量试验[J].导航与控制，2013，12(4)：75-78.

[8] 熊盛青，周锡华，郭志宏，等.航空重力勘探理论方法及应用[M].北京：地质出版社,2010.

[9] Krasnov A A, Nesenyuk L P, Peshekhonov V G ,et al.Integrated marine gravimetric system.Development and operation results[J].Gyroscopy and Navigation, 2011,2(2):75-81.

[10] Instruction manual of model “S” Air_Sea Dynamic Gravity Meter System[DB/OL].http://www.mic roglacoste.com.

[11] Abbasi M, Barriot J P, Verdun J.Airborne LaCoste & Romberg gravimetry: a space domain approach[J].Journal of Geodesy, 2007(81):269-283.

[12] Olesen A V, Forsberg R, Gidskehaug A.Airborne gravimetry using the LaCoste and Romberg gravimeter-an error analysis[C]//Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation.Banff, Canada, 1997:613-618.

[13] Olson D.GT_1A and GT_2A airborne gravimeters: Improvements in design, operation, and processing from 2003 to 2010[C]//Airborne Gravity, 2010:152-171.

[14] Berzhitzky V N, Bolotin Y V, Golovan A A, et al.GT_1A inertial gravimeter system:Results of flight tests[C]//MSU Faculty of Mechanics and Mathematics.Moscow, Russia, 2002.

[15] Sander S, Argyle M, Elieff S, et al.The AirGrav airborne gravity system[C]//Airborne Gravity, 2004:49-54.

[16] Argyle M, Ferguson S, Sander L, et al.AIRGrav results: a comparison of airborne gravity data with GSC test site data[J].The Leading Edge, 2000, 19(10):1134-1138.

[17] Glennie C L, Schwartz K P, Bruton A M, et al. A comparison of stable platform and strapdown airborne gravity[J].Journal of Geodesy, 2000, 74(5):383-389.

[18] Senobari M S.New results in airborne vector gravimetry using strapdown INS/DGPS[J].Journal of Geodesy, 2010,84(5):277-291.

[19] Glennie C, Schwarz K P.A comparison and analysis of airborne gravimetry results from two strapdown inertial/DGPS systems[J].Journal of Geodesy, 1999, 73(6):311-321.

[20] Wei M, Schwarz K P.Flight test results from a strapdown airborne gravity system[J].Journal of Geodesy, 1998, 72(6):323-332.

[21] Bruton A M, Hammada Y, Ferguson S, et al.A comparison of inertial platform, damped 2_axis platform and strapdown airborne gravimetry[C]//Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation.Banff, Alberta, 2001.

Applications and Data Processing of Strapdown Gravimeter in Marine Gravity Survey

LUO Cheng, XUE Zheng-bing, LI Dong-ming, LI Hai-bing, WANG Wen-jing, MA Cun-zun

(Beijing Institute of Aerospace Control Devices，Beijing 100039，China)

According to requirements of marine gravity survey for gravimetry, a strapdown marine gravimeter named SAG-2M is developed, of which the system structure, working principle, features and data processing flow are discussed.And the system precision is evaluated based on some marine gravity survey which is carried out lately.Results showes that the differences of repeat survey lines are quite small, and the crossover differences is about 1.2mGal, demonstrating that the system could meet the specifications of marine gravity survey.

Strapdown INS; GPS; SAG-2M; Gravity anomaly

2017-05-16；

2017-06-05

国家国际科技合作专项(2014DFR80750)；航天科技集团公司九院创新基金项目(动基座重力测量系统，航空重磁一体化综合信息系统)

罗骋(1983-)，男，博士，高级工程师，主要从事动基座重力测量系统、高精度重力数据处理、导航算法等方面的研究。E-mail:whutluocheng@163.com

10.19306/j.cnki.2095-8110.2017.04.005

P716+.81

A

2095-8110(2017)04-0036-07