基于统计能量分析的船舶舱室阻尼降噪布置优化

吴卫国，魏杰证，林永水，范明伟，甘进

1武汉理工大学交通学院，湖北武汉430063 2武汉理工大学工程结构与力学系，湖北武汉430070 3中国舰船研究设计中心，湖北武汉430064

基于统计能量分析的船舶舱室阻尼降噪布置优化

吴卫国1，魏杰证1，林永水2，范明伟3，甘进1

1武汉理工大学交通学院，湖北武汉430063 2武汉理工大学工程结构与力学系，湖北武汉430070 3中国舰船研究设计中心，湖北武汉430064

［目的］对船舶舱室噪声阻尼控制进行布置优化研究，以提高阻尼减振降噪效果和降低阻尼重量。［方法］首先，基于SEA理论，对声腔子系统的A计权声压级关于子系统阻尼损耗因子的一阶灵敏度进行理论推导与数值分析。同时，提出阻尼材料的布置数学优化模型并设计优化程序，运用MATLAB对VA One进行二次开发，建立舱室噪声阻尼控制布置优化系统。然后，在此基础上，将阻尼敷设分为5个区域，每个区域的阻尼厚度比为优化变量，以阻尼涂层的总重量为目标函数，以目标舱室的A计权声压级为约束条件，建立实船SEA优化模型并进行布置优化数值研究。［结果］研究结果表明，通过优化程序计算可以得到各区域阻尼敷设的最佳厚度，优化后的阻尼重量可减轻60.4%，有效提高了单位重量阻尼的降噪效果。［结论］该研究成功解决了舱室阻尼降噪的阻尼敷设位置和厚度的选择难题，为阻尼的声学设计提供了可靠的分析方法和指导。

舱室噪声；统计能量分析；声阻尼；降噪；优化设计；二次开发

0 引 言

船舶舱室噪声控制通常从声源、传递途径和接受者这3个环节来综合考虑。一旦主机、螺旋桨等噪声源确定，降低船体板的振动声辐射、抑制结构声的传递及增加结构振动能量的衰减就成为降噪的关键。阻尼技术在以上几个方面均可发挥有效作用，因此在船舶舱室噪声控制中得到了广泛应用。

在船舶舱室噪声阻尼控制的研究领域，国内外学者开展了深入研究。文功启［1］研究指出阻尼材料敷设在船舶机舱和舵机舱的底板及桁材的减振降噪效果更好。于大鹏等［2］研究了阻尼结构对舱室噪声的影响，发现在激励源舱室敷设阻尼材料的情况下降噪不明显，但对非声源舱室有降噪作用，并且自由阻尼材料比约束阻尼材料的降噪效果更好；对于非激励源舱室敷设阻尼材料的情况，该方法可起到降噪的作用，并且与自由阻尼材料相比约束阻尼材料的效果更好。蔡旭龙［3］对某船舶生活舱室采用阻尼材料和吸声材料的降噪效果进行了研究与分析，研究结果表明，通过采取阻尼降噪措施，可以较好地改善各类舱室的噪声水平。林永水［4］分析了在声波传递路径上敷设自由阻尼材料和约束阻尼材料对结构振动响应的影响，比较了阻尼材料连续敷设和间断敷设时的减振效果，但未直接对阻尼材料的降噪效果进行优化分析。范明伟［5］运用 MATLAB对 VA One软件的优化功能进行二次开发，并应用到了机舱的阻尼降噪优化分析中，但研究并未建立一个广义的优化数学模型，计算效率和可靠性有待提高。

综合分析可知，目前的阻尼减振降噪方法还处于粗放模式阶段，阻尼材料敷设的位置及厚度等主要依据工程经验来确定，甚至是采取在整个局部结构中均匀敷设阻尼材料。这种方式使阻尼材料的重量急剧增大，而降噪效果并未得到显著提高，所以如何使用最少的阻尼材料达到最佳的减振降噪效果正成为一个在科学与工程上需要迫切解决的问题。一方面，在给定重量约束的条件下，通过选择合适的阻尼材料以及合理布置，以提高单位阻尼重量的减振降噪效果来实现减振降噪目标；另一方面，在给定减振降噪值的约束条件下，通过选择合适的阻尼材料以及合理布置，以降低每分贝噪声值的阻尼重量来满足重量控制目标。因此，当阻尼材料选定后，阻尼材料的布置优化对阻尼减重和降噪的效果将起到十分重要的作用。

目前，对舱室噪声进行分析有多种方法，主要包括统计能量分析（Statistical Energy Analysis，SEA）法、有限元法（FEM）和边界元方法（BEM）、SEA-FE混合方法以及基于实船测试噪声数据的经验公式法。上述方法中，SEA方法适用于结构的高频声振问题分析［6］，FEM方法主要用于解决低频声振问题，Shorter和 Langley［7］提出的 SEA-FE混合方法主要用于解决中间频段的声振特性分析。国外很早就采用SEA方法来预报船舶舱室噪声［8-10］。在国内，郦茜和吴卫国［11］以及于大鹏等［2］采用SEA方法预报了舱室噪声；邱斌等［12］基于VA One软件首次将船舶舱室噪声预报扩展到全频段，在中间频段采用SEA-FE混合方法，对船舶舱室噪声进行了全频段预报。

鉴于船舶的复杂性，目前舱室噪声的数值预报主要还是采用SEA方法。本文拟基于SEA方法对船舶舱室的阻尼降噪布置进行优化分析。首先，对声腔A计权声压级关于阻尼损耗因子的灵敏度开展研究，探讨敷设位置和阻尼损耗因子对舱室噪声的影响；其次，提出优化数学模型和优化程序，集成MATLAB的优化功能和VA One软件的SEA求解功能，建立阻尼控制优化的分析平台；最后，开展船舶舱室噪声阻尼布置优化的数值实验研究，为船舶舱室噪声的阻尼声学设计提供建议。

1 基于SEA的阻尼灵敏度分析

1.1 一阶灵敏度分析模型

根据互易原理，给出如下功率流平衡方程：

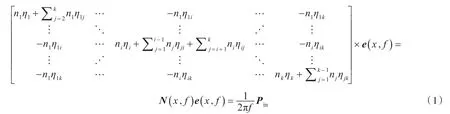
式中：k为统计能量子系统的数量；ni，ηi分别为子系统i的模态密度和内损耗因子；ηij(ηji)为子系统i(j)和子系统 j(i)的耦合损耗因子；N(x ，f)为损耗因子矩阵，是正定对称矩阵，假设它对设计变量x是连续可微的；e(x ，f)为模态能量矩阵，e(x ，f)=[e1， e2， … ， ek]T；Pin为 独立于设计变量的输入功率向量。

通过式（1）推导的模态能量矩阵为［13］

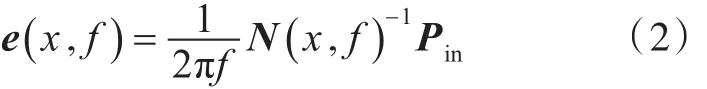
式中，中心频率带宽内的总能量E(x ，f )可用该中心频率下的模态密度n(x ，f)和模态能量矩阵e(x ，f )来表达：

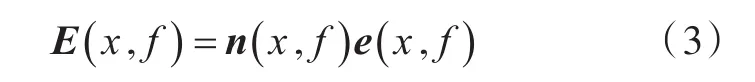
式中：n(x ，f)为由子系统模态密度组成的对角矩阵。

声腔子系统Q在中心频率 fj下的声压PQ(fj)计算公式如下：

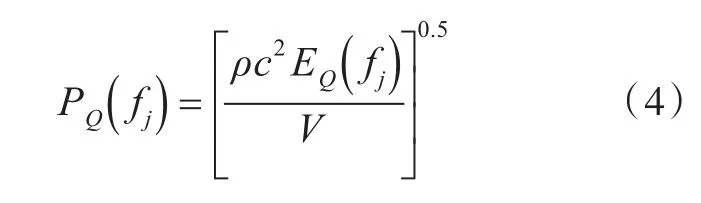
式中：ρ为空气密度；c为空气中的声速；V为声腔体积；EQ(fj)为声腔子系统Q中心频率 fj带宽内的总能量。

中心频率 fj下声腔子系统Q的声压级LPQ(fj)计算公式为

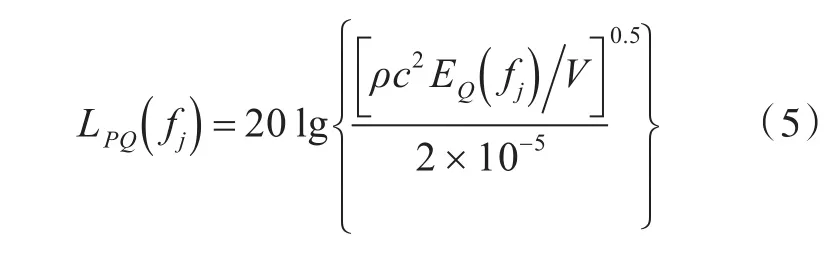
整个计算频域内声腔子系统Q的A计权声压级LPAQ()

f计算公式为

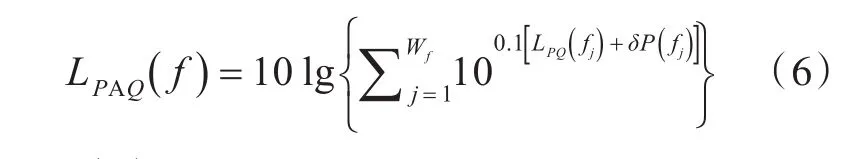
式中：δP(fj)为中心频率 fj下A计权声压级的修正值；Wf为整个计算频域内中心频率的个数。

1.2 A计权声压级关于设计变量的一阶灵敏度分析

对于设计变量X=[x1， x2， …， xk] ，推导声腔子系统能量关于子系统阻尼损耗因子的灵敏度时，假定设计变量中单个子系统的内损耗因子改变，然后将其扩展到多个变量值。

由式（3），得到总能量关于设计变量x的一阶灵敏度为

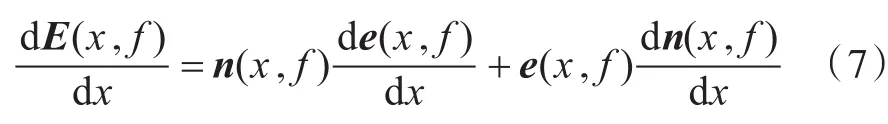
假定输入功率向量Pin与设计变量x相互独立，因此，对式（1）求导可得

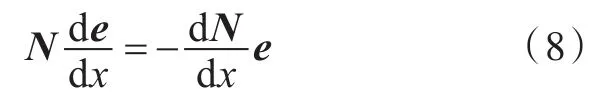
N关于设计变量x的导数为

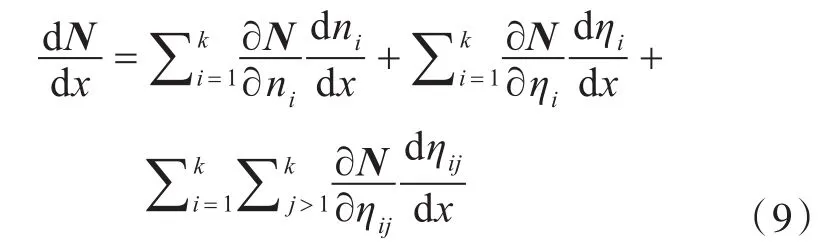
板子系统的模态密度n(f)为

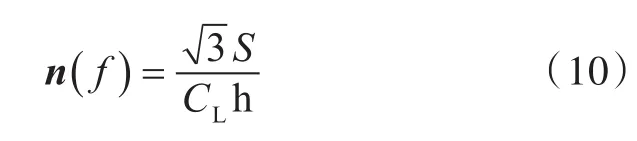
式中：CL，h分别为纵波波速及板的厚度；S为声腔总的表面积。

声腔子系统的模态密度为

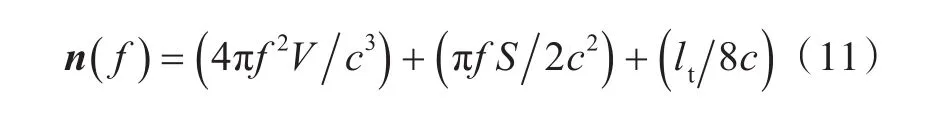
式中，lt为声腔的总周长。

板子系统的内损耗因子为［9］

声腔子系统的内损耗因子为［10，14］

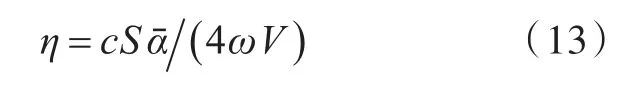
式中：αˉ为声腔的平均吸声系数；ω=2πf，为角频率。

板子系统i与板子系统 j的连接耦合损耗因子 ηij为［6］

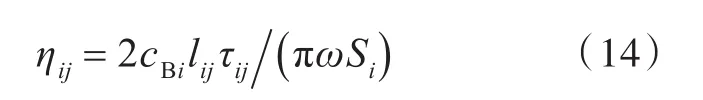
式中：cBi为板中弯曲波的波速；τij为板子系统间传递系数；Si为板子系统i的面积；lij为结构间连接长度。

板子系统i与声腔子系统 j的耦合损耗因子ηij为［6］

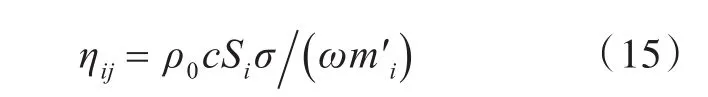
式中：ρ0为声腔中流体密度；m′i为板子系统i的面密度；σ为辐射比。

声腔与声腔之间的耦合损耗因子ηij为［6］

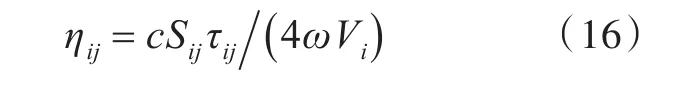
式中：Sij为声腔子系统i和声腔子系统 j面连接的面积；τij为声腔子系统间传递系数；Vi为声腔子系统i的体积。

当设计变量值x为第i个板子系统的阻尼损耗因子 ηi，即 x=ηi时，将式（12）～式（16）代入式（19），可得

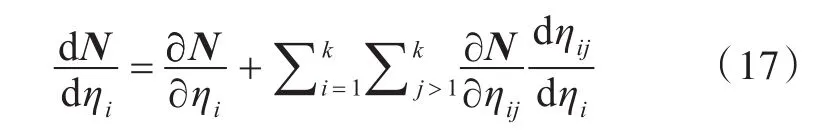
对于扩散声场，第i个板子系统相关的耦合损耗因子ηij相对于第i个板子系统的阻尼损耗因子 ηi是独立的，即，因此，式（17）右端可简化为一个k×k阶矩阵，该矩阵k(i ，i)=ni，其他元素均为0。

由式（2）和式（8），可得

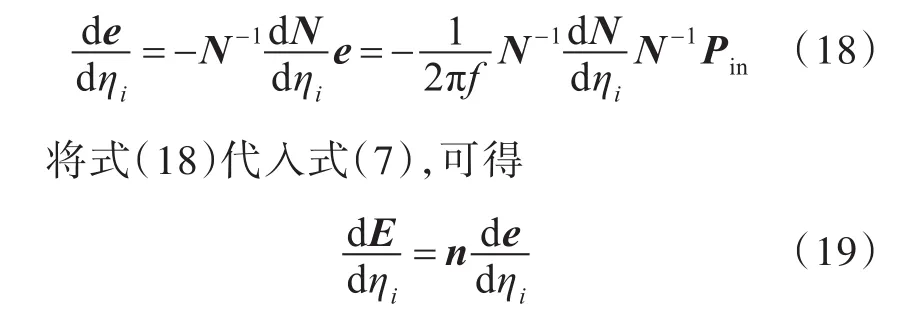
由此，声腔子系统Q的总能量EQ关于第i个板子系统的内损耗因子的灵敏度为

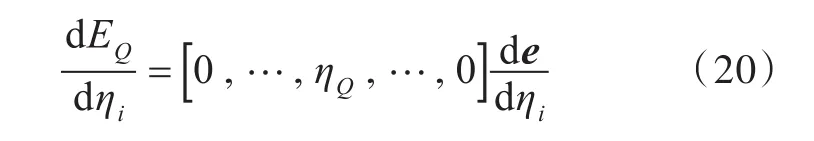
式中，ηQ为声腔子系统Q的内损耗因子。

对式（5）两边关于设计变量η求导，可得

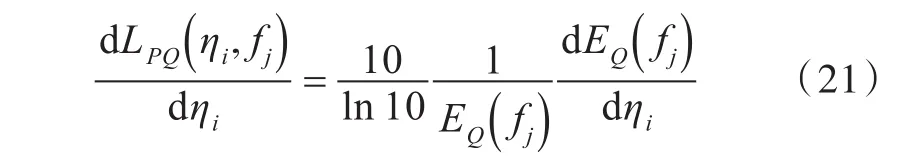
对式（6）两边关于设计变量η求导，可得

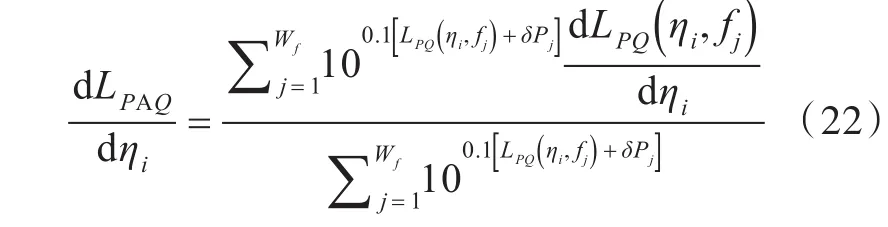
将式（20）代入式（21），可得

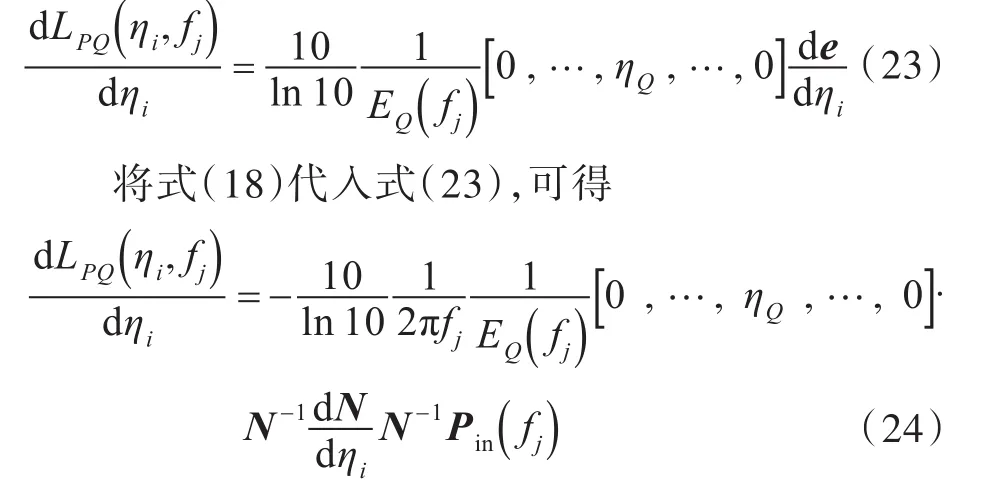
式中，Pin(fj)为中心频率 fj下的输入功率。

将式（24）代入式（22），得到目标函数的一阶灵敏度表达式

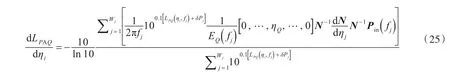
1.3 灵敏度数值分析

模型由2个9 m×6 m×3 m的长方形舱室组成，两者尺度和结构属性相同，如表1所示。整个系统SEA模型包含2个声腔子系统和11个板子系统。图1所示为子系统划分情况，其中：1为声源室的声腔子系统，子系统2～7分别为声源室的板子系统；子系统13为非声源室的声腔子系统，子系统 2，8，9，10，11，12为非声源室的板子系统。结构声激励作用于板子系统6，空气声激励作用于声腔子系统1。

图2所示为在空气声激励作用时，对声源舱室声腔子系统和非声源舱室声腔子系统的A计权声压级关于阻尼损耗因子的一阶灵敏度的分析结果。结果表明，空气声激励作用时，改变了板子系统的阻尼损耗因子，对声源舱室A计权声压级的影响甚微，对非声源舱室的影响较大；而传递途径上板子系统（子系统2）的阻尼损耗因子对非声源舱室A计权声压级的影响明显。

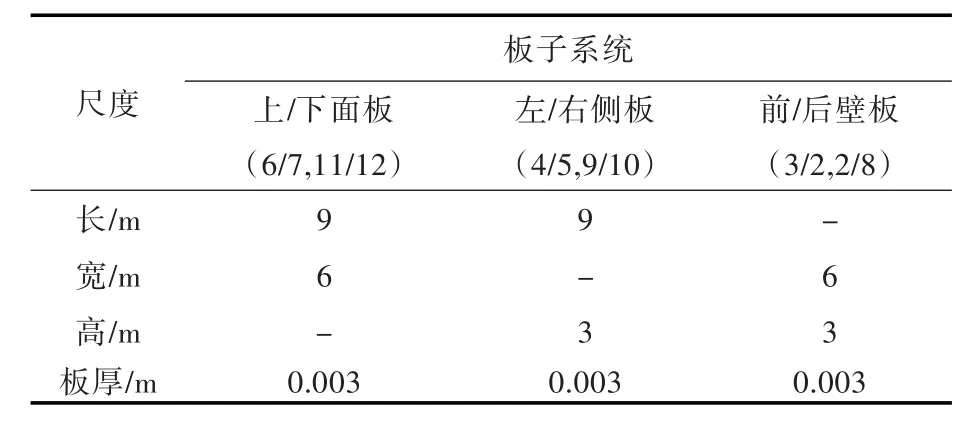
表1 舱室的特征参数Table 1 The characteristic parameters of a single cabin

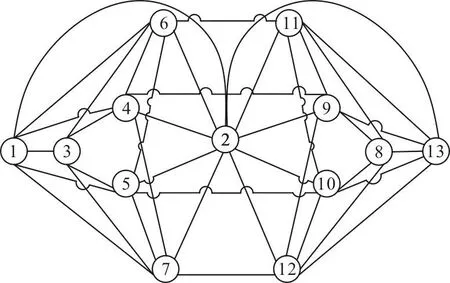
图1 舱室的SEA子系统划分图Fig.1 The cabin SEA subsystems demarcation plan

图3所示为在结构声激励作用时，对声源舱室声腔子系统和非声源舱室声腔子系统的A计权声压级关于阻尼损耗因子的一阶灵敏度的分析结果。结果表明，结构声激励作用时，改变了板子系统的阻尼损耗因子，对两种舱室A计权声压级影响较大，尤其是改变了激励作用区的阻尼损耗因子。因此，采用阻尼材料来降低噪声将会取得显著的效果，尤其是阻尼材料敷设在激励作用区时。

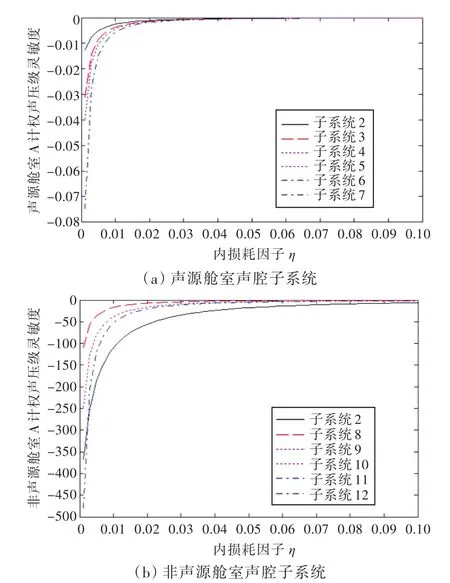
图2 空气声激励时声源舱室和非声源舱室声腔子系统A计权声压级关于阻尼损耗因子一阶灵敏度分析Fig.2 The first-order sensitivity analysis of A-weighted sound pressure level about damping loss factor for acoustic and non-acoustic source cavity subsystem under the action of air acoustic excitation

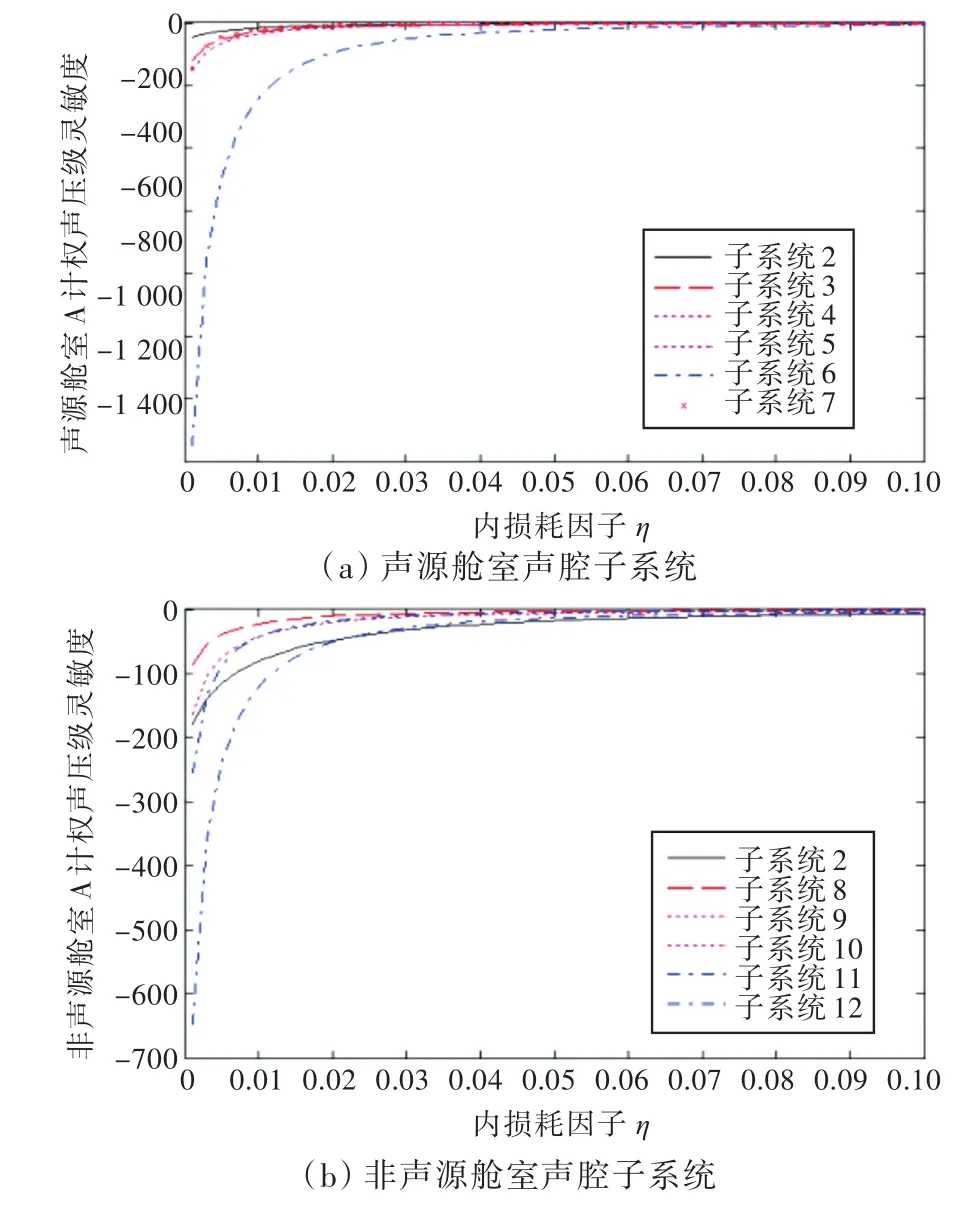
图3 结构声激励时声源舱室和非声源舱室声腔子系统A计权声压级关于阻尼损耗因子一阶灵敏度分析Fig.3 The first-order sensitivity analysis of A-weighted sound pressure level about damping loss factor for acoustic and non-acoustic source cavity subsystem under the action of structure-borne sound excitation

此外，由图2和图3还可以看出，在内损耗因子η=0.02附近，灵敏度值呈现陡峭的变化趋势；当η=0.02～0.1时，灵敏度变化趋缓；当η＞0.1时，灵敏度值几乎不变，这说明当板子系统的阻尼损耗因子从0增加到0.1时，对声腔的A计权声压级有较明显的影响，而阻尼值继续增加时，对其影响甚微。因此，当阻尼厚度达到一定值后，继续增加厚度，其降噪效果并不会显著增加。

2 基于SEA的舱室阻尼降噪布置优化

2.1 舱室阻尼降噪布置优化数学模型

假设规范规定的船舶目标舱室G的A计权声压级的限制值为LPAGH，未敷设阻尼材料时目标舱室初始的A计权声压级为LPAGI。舱室噪声阻尼布置优化问题的约束条件为目标舱室的噪声级满足规范要求，且阻尼总重量最轻。

如图4所示，该模型将阻尼材料敷设分为M个区域，第i个区域的底材厚度为ti，面积为Si，阻尼层厚度为h1i，约束层厚度为h2i，ρ1和 ρ2分别为自由阻尼层及约束层密度，阻尼材料与底材的厚度比 yi=(h1i+h2i)ti。约束层厚度h2i用变量 yi表示为

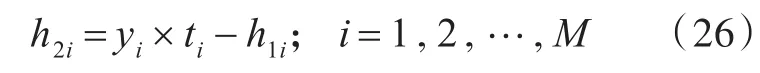
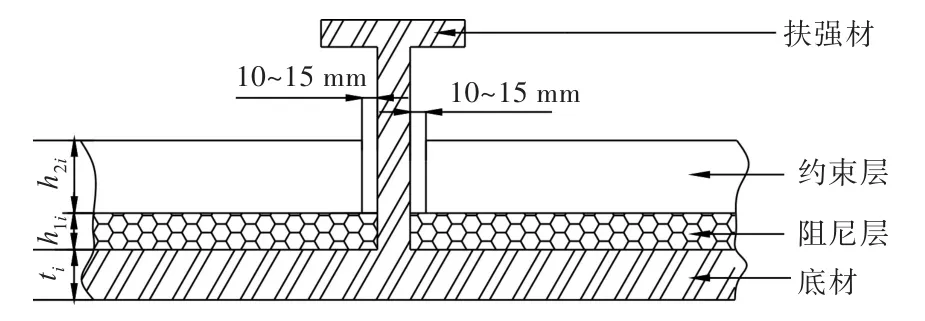
图4 约束阻尼结构示意图Fig.4 Schematic of constraint damping structure

根据文献［5］，敷设阻尼钢板的复合损耗因子随阻尼层厚度的增加而增大，当阻尼层与底材的厚度比大于一定值时，复合损耗因子增加的速率降低，定义此时厚度比为临界厚度比。因此，阻尼厚度比的上限值取 yc，有

优化数学模型中约束条件是目标舱室G的A计权声压级的减少量δG≥LPAGI-LPAGH。设敷阻尼材料之后舱室的A计权声压级为LPAG()Y ，则目标舱室声压级约束条件可以改写为

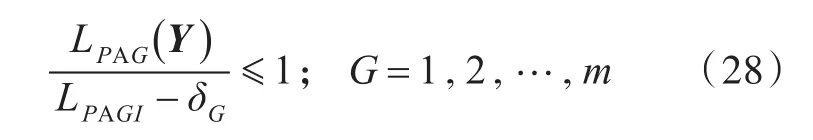
式中：Y=[ y1，y2， …， yM]。

根据多元函数不等式约束优化问题的求解方法，数学优化模型可以表述为：

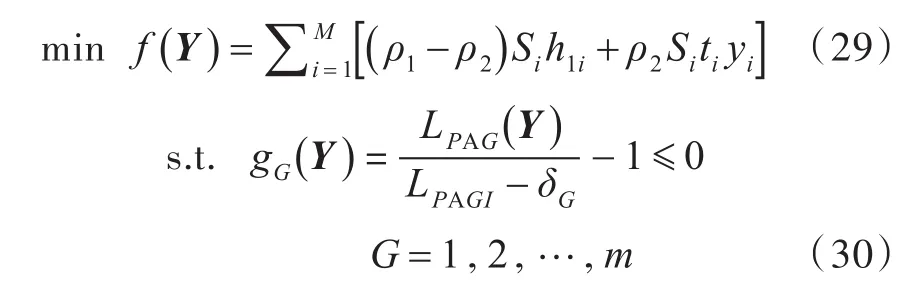
式中：f(Y)为目标函数；gG(Y)为约束条件的梯度，其矩阵分别表示如下：

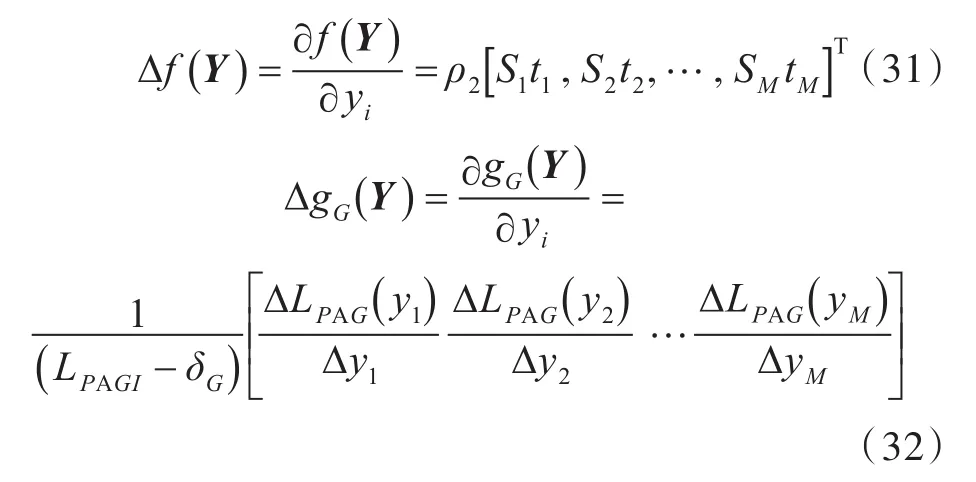
式中，Δyi为设计变量的变化值。

2.2 优化算法和优化函数

在求解优化问题的过程中，将同时采用解析方法和数值方法。解析方法使用到拉格朗日函数，拉格朗日函数必须满足Kuhn-Tucker条件［15］。

对于式（29）中的设计变量向量，Y=[y1，y2，…，yM]T为 M维向量，它受到m个不等式约束的限制。γ是对应于不等式约束的拉格朗日乘子向量，γ=[γ1， γ2，…，γm]T，并有非负的要求。在使用拉格朗日乘子法推导出相应的极值条件时，需要引入m个松弛变量，χ=[χ1，χ2，…，χm]T，使式（30）中的不等式约束gj(Y)≤0(j=1，2，…，m)变成等式约束从而组成相应的拉格朗日函数，即

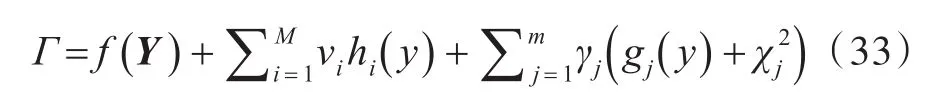
式中：ν=[ ν1，ν2，…，νM]，为拉格朗日乘子向量。

根据式（33），可得Kuhn-Tucker条件为

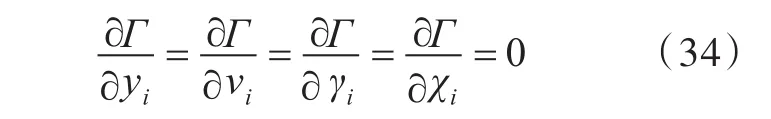
文中采用MATLAB自带的优化函数fmincon进行求解，具体的优化算法是序列二次规划法。

2.3 基于VA One和MATLAB的优化程序设计

程序以VA One软件为SEA模型声压级计算的求解器，MATLAB为主控程序，提供优化算法，两者之间的数据交换通过API函数实现。首先，在VA One中建立优化所用的SEA模型，并在预定的区域敷设阻尼材料，作为初始输入模型。其次，在MATLAB中定义目标函数与设计变量，通过API函数对输入模型进行参数修改，即厚度比。然后，用VA One计算目标舱室G的A计权声压级，并通过API函数数据接口将计算后的目标值传递给MATLAB程序，程序根据返回值判断是否满足约束条件。如此循环下去，直到获得最优结果，具体流程见图5。

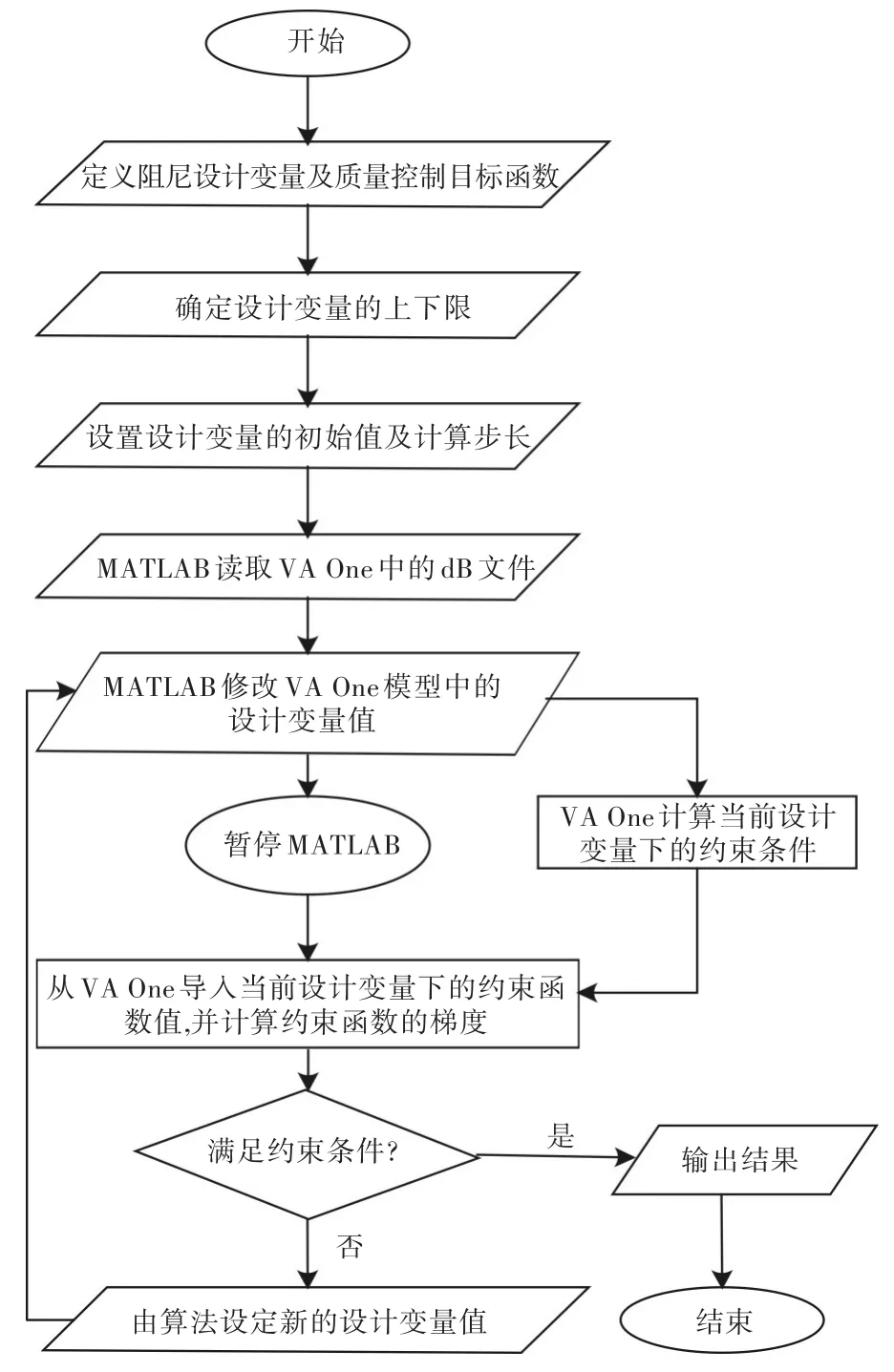
图5 阻尼控制优化布置二次开发程序流程图Fig.5 Flow chart of secondary development program for layout optimization of damping control

2.4 阻尼材料布置优化数值分析

计算模型为一艘巡逻艇的SEA模型，目标舱室取2个噪声超标的舱室（会议室和驾驶室），降噪值分别为δ1≥8dB和δ2≥9dB。阻尼材料采用化工部海洋涂料研究所研制的无溶剂阻燃型船用阻尼涂料T54/T60，阻尼参数如表2、表3及图6所示。图6中同一种颜色代表涂区敷设的阻尼层厚度相等。根据文献［16］，阻尼层厚度h1i=0.001m，阻尼厚度比上限值yc=2。

T54/T60复合损耗因子计算采用谱有限元法［18］，第i个波型的阻尼损耗因子ηi公式如下：

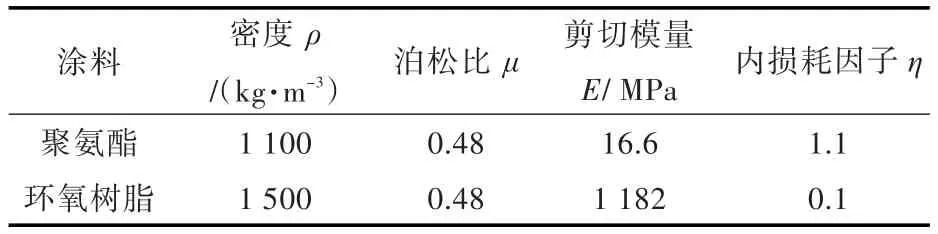
表2 聚氨酯和环氧树脂属性［17］Table 2 The properties of polyurethane and epoxy

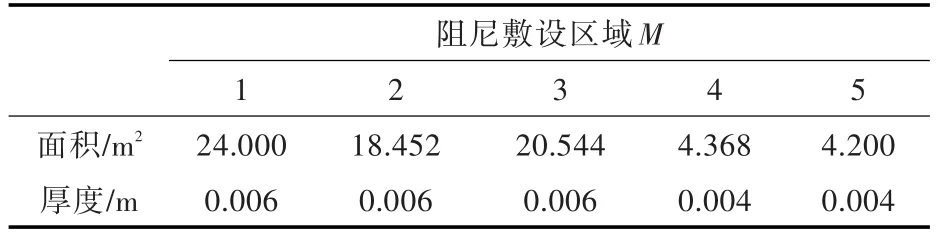
表3 阻尼区域面积与底板厚度Table 3 Damping area and plate's thickness

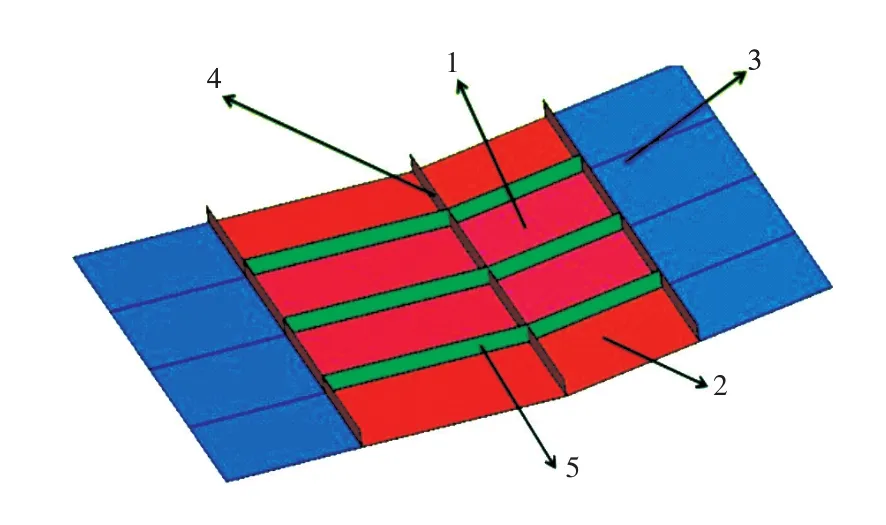
图6 板系统阻尼敷设示意图Fig.6 Schematic of damping layout for plate system

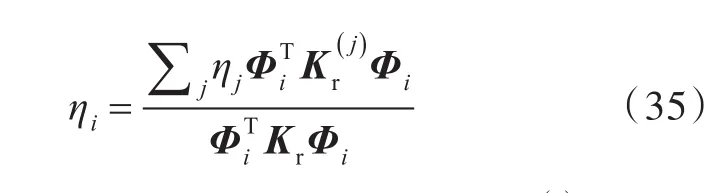
式中：ηj为第 j层的阻尼损耗因子；为第j层的刚度矩阵；Kr为总的刚度矩阵；为第 i个波型对应横截面的位移特征向量。

阻尼厚度比向量取初始值Y=[1.5，1.5，1.5，1.5，1.5]，目标函数初始值为 691.3 kg，程序运行约4 h，经过6次迭代完成优化求解，厚度比的计算结果如图7所示。从图8可以看出，目标函数的最优解为273.9 kg，此时会议室和驾驶室的噪声水平满足规范的要求，同时阻尼涂料T54/T60的质量也最轻。此时，与阻尼厚度比向量对应的阻尼厚度为结合工程实际，根据优化结果取约束层厚度

本文采用统计能量分析方法对船舶舱室噪声的阻尼降噪布置优化进行了研究，提出阻尼布置的数学优化模型及程序，并运用MATLAB对VA One软件进行二次开发，建立了噪声阻尼控制布置的优化系统。通过对实际船舶舱室的阻尼材料降噪布置优化数值分析，得到如下结论：

1）当空气声激励时，阻尼材料对声源舱室的降噪效果甚微；当结构声激励时，阻尼的降噪效果显著，且在激励作用区域敷设约束阻尼降噪效果最佳，在传递路径上敷设自由阻尼的效果次之；阻尼厚度达到一定值后，降噪效果并不会随阻尼厚度的增加而显著增加。此时会议室和驾驶室的A计权声压级分别为69.13和69.99 dB，满足控制要求，阻尼涂料T54/T60的质量为273.7 kg，较初始设计值的重量减轻了60.4%。

由图7和图8可知，子系统1在3个底板子系统中敷设的约束阻尼厚度最大，说明阻尼材料布置在子系统1降噪的效果最好，且激励作用在子系统1上，也说明阻尼材料布置在激励作用区域更能发挥阻尼材料的减振降噪作用。子系统2，3的阻尼约束层可以忽略，说明在声振动传递路径上采用自由阻尼即可。子系统4，5的阻尼层较厚，说明船底肋板和纵桁是能量传递的重要途径，尤其是横向构件，其敷设约束阻尼材料后更能大幅降低能量的传递。总之，优化结果说明了非均匀敷设阻尼材料较均匀敷设的效果更佳，合理布置阻尼敷设材料的位置与厚度，可大幅提高阻尼减振降噪的效果，并减轻阻尼材料的重量。

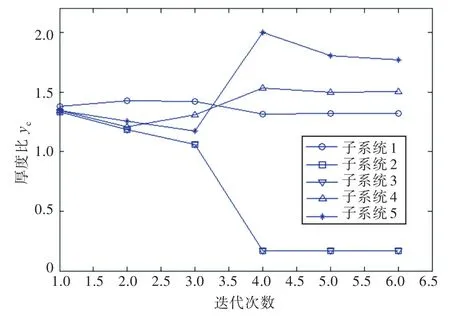
图7 每一次迭代厚度比的取值Fig.7 The thickness ratio values of each iteration

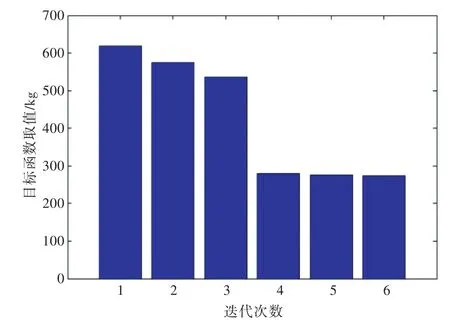
图8 每一次迭代目标函数的取值Fig.8 The objective function values of each iteration

3 结 论

2）结构横向和纵向强构件是结构声传递的重要通道，敷设约束阻尼材料可抑制结构噪声的传递，有效降低非声源舱室的噪声。

3）与传统的阻尼材料均匀布置方式相比，优化后的阻尼材料布置可显著提高单位阻尼质量的降噪效果。

本研究结果可为舱室噪声阻尼控制中阻尼材料敷设位置和厚度的选择提供可靠的分析方法，并为其声学设计提供指导。

［1]文功启.高速船结构噪声传播及其阻尼被动控制的研究［D］.武汉：武汉理工大学，2002.WEN G Q.Research of the propagation of the struc⁃ture-borne noise in high-speed ship and the inactive noise controlling by damping treatments［D］.Wuhan：Wuhan University of Technology，2002（in Chinese）.

［2]于大鹏，赵德有，汪玉.船舶声学建模和阻尼结构对舱室噪声影响研究［J］.船舶力学，2010，14（5）：539-548.YU D P，ZHAO D Y，WANG Y.Influence of damped material and the ship model of acoustic on the ship cab⁃in noise［J］.Journal of Ship Mechanics，2010，14（5）：539-548（in Chinese）.

［3]蔡旭龙.AHTS的舱室噪声预报及控制研究［D］.广州：华南理工大学，2016.CAI X L.Study on the cabin noise in AHTS about the prediction and control［D］.Guangzhou：South China University of Technology，2016（in Chinese）.

［4]林永水.钢铝混合结构高速船声振传递分析与控制研究［D］.武汉：武汉理工大学，2011.LIN Y S.Research on vibration and noise transmission and control for steel-aluminum mixed structure high-speed ship［D］.Wuhan：Wuhan University of Technology，2011（in Chinese）.

［5]范明伟.高速船舱室噪声的统计能量分析与降噪优化研究［D］.武汉：武汉理工大学，2012.FAN M W.Prediction and optimization of cabin noise of high-speed ship based on statistical energy analysis method［D］.Wuhan：Wuhan University of Technolo⁃gy，2012（in Chinese）.

［6]LYON R H，DEJONG R G.Theory and application of statistical energy analysis［M］.2nd ed.London：Butter⁃worth-Heineman，1995：3021.

［7]SHORTER P J，LANGLEY R S.Vibro-acoustic analy⁃sis of complex systems［J］.Journal of Sound and Vibra⁃tion，2005，288（3）：669-699.

［8]JENSEN J J.Calculation of structureborne noise trans⁃mission in ships using the“statistical energy analysis”approach［C］//Proceedings of International Symposium on Shipboard Acoustics.Noordwijkerhout：British Ship Research Association，1976：303.

［9]IRIE Y，NAKAMURA T.Prediction of structure borne sound transmission using statistical energy analysis［J］.Bulletin of the Marine Engineering Society in Ja⁃pan，1985（13）：60-70.

［10]HYNNÁ P，KLINGE P，VUOKSINEN J.Prediction of structure-borne sound transmission in large welded ship structures using statistical energy analysis［J］.Journal of Sound and Vibration，1995，180（4）：583-607.

［11]郦茜，吴卫国.基于AutoSEA的高速船静噪声预报与控制［J］.中国舰船研究，2008，3（1）：28-30.LI Q，WU W G.Prediction and control of noise based on AutoSEA for high-speed vessels［J］.Chinese Jour⁃nal of Ship Research，2008，3（1）：28-30（in Chi⁃nese）.

［12]邱斌，吴卫国，刘恺.高速船全频段舱室噪声仿真预报［J］.中国舰船研究，2011，6（6）：49-53.QIU B，WU W G，LIU K.Full spectrum simulation prediction of high-speed vessel cabin noise［J］.Chi⁃nese Journal of Ship Research，2011，6（6）：49-53（in Chinese）.

［13]CHAVAN A T，MANIK D N.Sensitivity analysis of vibro-acoustic systems in statistical energy analysis framework［J］.Structural and Multidisciplinary Opti⁃mization，2010，40：283-306.

［14]CREMER L，HECKL M，PETERSSON B A T.Struc⁃ture-borne sound：structural vibrations and sound ra⁃diation at audio frequencies［M］.Berlin：Spring⁃er-Verlag，2005.

［15]唐焕文，秦学志.实用最优化方法［M］.3版.大连：大连理工大学出版社，2004.TANG H W，QIN X Z.Practical methods of optimiza⁃tion［M］.3rd ed.Dalian：Dalian University of Tech⁃nology Press，2004（in Chinese）.

［16]刘东晖，黄微波，杨宇润，等.T54/T60阻尼涂料在舰船减振降噪工程中的应用［J］.船舶，1997（4）：40-46.LIU D H，HUANG W B，YANG Y R，et al.Contribu⁃tions of T54/T6O damping coatings to noise and vibra⁃tion reduction for ships［J］.Ship&Boat，1997（4）：40-46（in Chinese）.

［17]WANG B Z，HUANG W B，HUANG B C，et al.Damping properties of polyurethane/epoxy resin com⁃posites［J］.China Synthtic Rubber Industry，2004，27（5）：323-323.

［18]SHORTER P J.Wave propagation and damping in lin⁃ear viscoelastic laminates［J］.Journal of the Acousti⁃cal Society of America，2004，115（5）：1917-1925.

Damping layout optimization for ship's cabin noise reduction based on statistical energy analysis

WU Weiguo1，WEI Jiezheng1，LIN Yongshui2，FAN Mingwei3，Gan Jin1
1 School of Transportation，Wuhan University of Technology，Wuhan 430063，China 2 Department of Mechanics and Engineering Structure，Wuhan University of Technology，Wuhan 430070，China 3 China Ship Development and Design Center，Wuhan 430064，China

An optimization analysis study concerning the damping control of ship's cabin noise was carried out in order to improve the effect and reduce the weight of damping.Based on the Statistical Energy Analysis(SEA)method,a theoretical deduction and numerical analysis of the first-order sensitivity analysis of the A-weighted sound pressure level concerning the damping loss factor of the subsystem were carried out.On this basis,a mathematical optimization model was proposed and an optimization program developed.Next,the secondary development of VA One software was implemented through the use of MATLAB,while the cabin noise damping control layout optimization system was established.Finally,the optimization model of the ship was constructed and numerical experiments of damping control optimization conducted.The damping installation region was divided into five parts with different damping thicknesses.The total weight of damping was set as an objective function and the A-weighted sound pressure level of the target cabin was set as a constraint condition.The best damping thickness was obtained through the optimization program,and the total damping weight was reduced by 60.4%.The results show that the damping noise reduction effect of unit weight is significantly improved through the optimization method.This research successfully solves the installation position and thickness selection problems in the acoustic design of damping control,providing a reliable analysis method and guidance for the design.

cabin noise； Statistical Energy Analysis(SEA)； acoustic damping;noise reduction；optimization design;secondary development

U661.44

A

10.3969/j.issn.1673-3185.2017.04.007

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170727.1025.024.html期刊网址：www.ship-research.com

吴卫国，魏杰证，林永水，等.基于统计能量分析的船舶舱室阻尼降噪布置优化［J］.中国舰船研究，2017，12（4）：41-48.

WU W G，WEI J Z，LIN Y S，et al.Damping layout optimization for ship's cabin noise reduction based on statistical energy analysi［sJ］.Chinese Journal of Ship Research，2017，12（4）：41-48.

2017-02-28< class="emphasis_bold">网络出版时间：

时间：2017-7-27 10:25

国家部委基金资助项目

吴卫国，男，1960年生，教授，博士生导师。研究方向：结构安全性、可靠性与舒适性。

E-mail：maijt@163.com

林永水（通信作者），男，1983年生，博士，讲师。研究方向：船舶振动噪声预报与控制。

E-mail：peakspylin@163.com