石墨烯剪纸的大变形拉伸力学行为研究∗

韩同伟李攀攀

(江苏大学土木工程与力学学院,镇江 212013)

(2016年10月13日收到;2016年11月8日收到修改稿)

石墨烯剪纸的大变形拉伸力学行为研究∗

韩同伟†李攀攀

(江苏大学土木工程与力学学院,镇江 212013)

(2016年10月13日收到;2016年11月8日收到修改稿)

将传统宏观剪纸技术应用于纳观尺度,通过引入圆角矩形切口图案构建了石墨烯剪纸.采用分子动力学方法研究了单层与双层石墨烯剪纸的大变形拉伸力学行为和变形破坏机制,并系统地研究了关于切口图案的3个无量纲几何参数对单层石墨烯剪纸的力学性能和变形破坏机制的影响规律.研究发现,通过引入规则切口,可以有效地大幅度提高石墨烯的延展性,其断裂应变可达到完美石墨烯的5—6倍.通过控制3个几何参数,可以有效地调控石墨烯的延展性和力学行为.研究结果表明,古老的剪纸技术为提高二维纳米材料延展性、实现光电纳米器件可延展柔性化提供了一种新的解决方案.

石墨烯,剪纸,大变形,分子动力学

1 引 言

石墨烯是单原子厚度新型二维纳米碳材料,被誉为新一代战略材料.由于独特的二维结构以及优异的晶体品质,石墨烯具有超常的电学、热学、磁学和力学性能,有望在高性能纳电子器件、复合材料、场发射材料、气体传感器、能量存储等领域获得广泛应用[1−3].研究表明,石墨烯的理想强度高达110—121 GPa,杨氏模量达到1 TPa[4],是人类已知强度最高的材料.就力学性能而言,石墨烯虽然具有高强度和高弹性模量,但其缺点是其拉伸应变仍然相对较低,可延展性差,一般小于30%[5,6],从而大大限制了其在柔弹性电子器件等应变工程领域的发展与应用.因此,如何改善和提高石墨烯等二维纳米材料以及电子器件的延展性是近年来力学及材料科学等领域的研究热点之一.

近年来,科研工作者通过巧妙的力学结构设计,如岛桥结构设计、折纸结构及其剪纸/折纸结构设计,较好地实现了电子器件的可延展柔性化[7−12]. 其中,剪纸/折纸(kirigam i/ origam i)[11,12]是一种古老的民间艺术,通过剪裁和折叠,可以将二维的纸张变成各种各样的复杂的三维图案和结构.最近,该技术工艺已从宏观研究尺度被逐渐引入到微/纳观尺度.科学家们基于此技术已成功制备了多种可延展柔性电子器件,如动态可延展太阳能电池、可延展锂离子电池、可延展石墨烯晶体管等[11−13].2015年,康奈尔大学M cEuen研究组[13]最早通过光刻实验技术成功制备了单层石墨烯平面剪纸,构建了石墨烯拉伸电极、石墨烯弹簧、石墨烯金字塔等多种新型结构,发现石墨烯剪纸具有很强的变形能力,而其电学性能在变形时并没有发生明显变化.这一研究结果表明,剪纸/折纸作为一种有效可控的方法,可以将石墨烯等单原子二维纳米材料制成可拉伸材料,从而拓展其在柔弹性电子器件和复合材料等领域的应用.波士顿大学Park研究组[14,15]采用分子动力学方法,研究了石墨烯、二硫化钼等二维纳米薄膜引入剪折图案后的大变形力学行为,发现屈服和断裂应变可以达到原来的3—4倍.但值得注意的是,剪折之后,其弹性模量和强度大大降低,均不到原来的1/10.因此,在设计材料结构提高其延展性的同时,尽可能保持其高模量和高强度也是值得注意的问题之一.

本文基于剪纸技术,采用分子动力学方法研究了石墨烯平面剪纸结构的拉伸力学行为,并构建了3个合理的无量纲剪折几何尺度参数和圆角矩形剪折图案,系统地研究了切口几何尺度参数对石墨烯的强度和应变等力学性能参数以及变形破坏机制的影响规律,为有效调控石墨烯等二维纳米尺度材料的力学性能提供理论基础和结构设计依据.

2 物理模型及模拟方法

2.1 石墨烯剪纸几何模型

完美的石墨烯是由单层六角元胞碳原子构成的蜂窝状二维晶体,其中碳碳键长约为0.142 nm.本文在构造石墨烯剪纸时,直接引入圆角矩形切口图案,边界不做任何化学修饰.石墨烯剪纸模型和重复单元分别如图1所示.主要几何参数如下:石墨烯剪纸的长度为L0,宽度为b,重复单元的宽度为d,内部切口高度为w,边缘切口高度统一控制为0.5w,切口宽度和圆角的直径均为c.一个典型的锯齿型石墨烯剪纸的模型如图1所示,其尺寸为L0=62.47 nm,b=25.56 nm,d=8.85 nm, w=17.04 nm,c=0.98 nm,原子个数为51267.在研究双层石墨烯剪纸时,堆积方式采用最为稳定的Bernal(AB)堆积[16],其模型尺寸和切口图案与图1单层石墨烯剪纸相同.

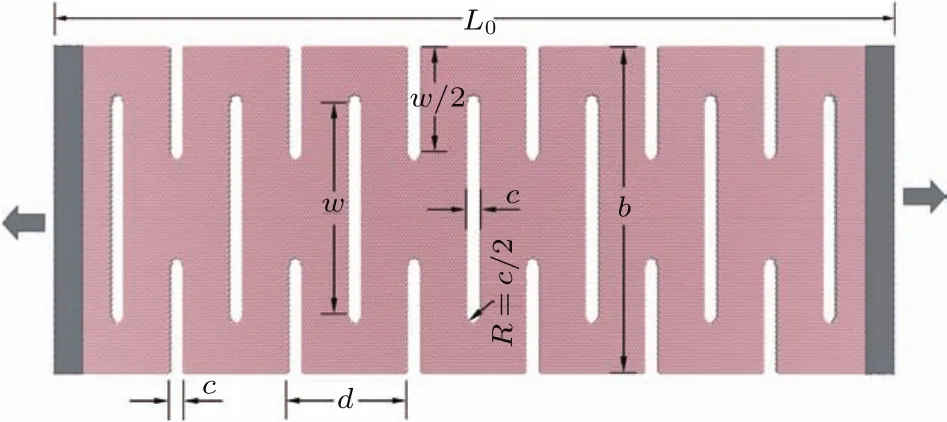
图1 (网刊彩色)石墨烯剪纸结构示意图Fig.1.(color on line)Schem atic sim u lation m odel of the graphene kirigam i tested.

2.2 模拟方法及过程

本文采用经典全原子分子动力学方法,其基本原理是通过原子间的相互作用势,求出每个原子所受到的力,在选定的时间步长、边界条件和初始条件下,对有限数目的原子建立其牛顿动力学方程组,用数值方法求解,得到这些原子的运动轨迹和速度分布,然后对足够长时间的结果求统计平均,从而得到所需要的宏观物理量和力学量.

分子动力学模拟是以势能函数为基础,势能函数的选取直接决定着模拟的精度.本文选择已得到广泛应用的REBO(reactive empiricalbond order)势函数[17]来描述单层石墨烯剪纸中碳原子之间的相互作用.REBO势函数是由Brenner等在Tersoff势函数[18]的基础上发展起来的一种多体势,可以很好地模拟C—C共价键的各种特性,包括键长、键角、键能、晶格常数和键的断裂重组等动态行为,能够较真实地反映碳元素所构成固态材料的物理性质.

REBO势函数表示为

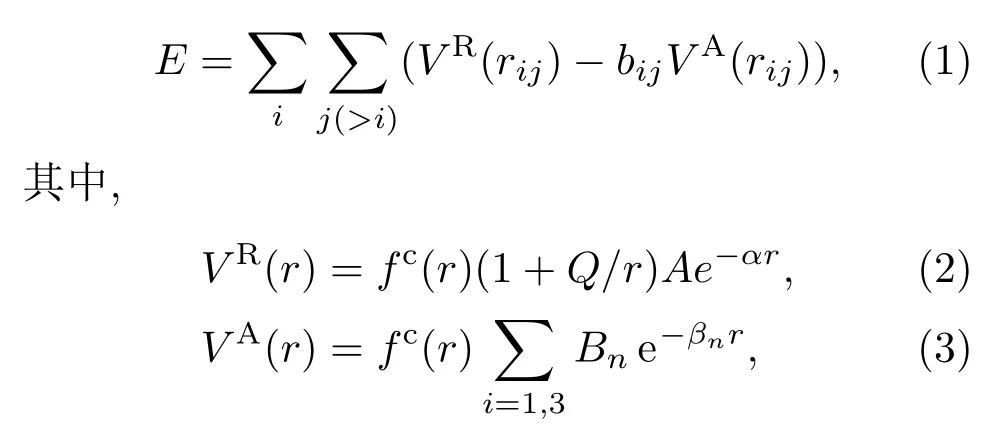
E是体系的总能量,VR和VA分别是对势的排斥项和吸引项,fc是光滑截断函数,bij为反映多体作用的键序函数,其具体形式见文献[17].

对于双层石墨烯剪纸,石墨烯层内的碳原子之间相互作用依然采用REBO势,石墨烯层间采用Lennard-Jones(LJ)12-6对势,即AIREBO势函数[19].AIREBO势实际上是REBO势的改进和推广,增加了长程相互作用项和扭曲项.

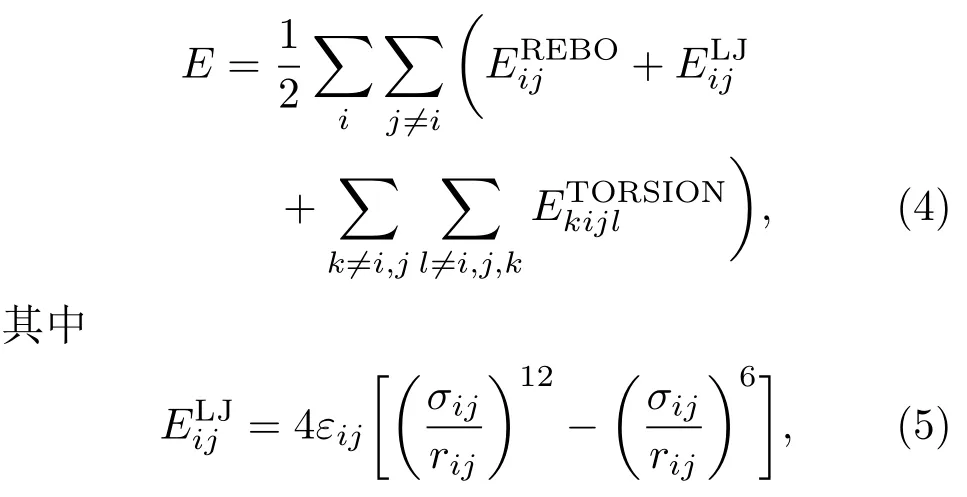
模型中C原子的质量取12.01,REBO势函数截断半径R取1.92Å,以消除石墨烯大应变断裂变形时产生的非物理现象[5,20,21].模拟石墨烯剪纸的拉伸破坏过程如下:首先在NVT系综下对初始构型进行无约束弛豫,使系统处于能量最低的平衡状态.然后对弛豫过的石墨烯剪纸沿x方向进行均匀拉伸,拉伸时固定石墨烯剪纸两端,施加均匀拉伸应变,应变率控制在1.0×109/s,直至石墨烯剪纸被拉伸破坏.为消除固定边界距离切口太近所造成的不良影响,本文在建立模型时,两固定端中间部分均为重复单元的整数倍(端部扣除切口宽度c),如图1所示.固定端的宽度均设置为所定义的石墨烯晶格长度(拉伸方向)的3倍,即锯齿型7.51Å,扶手椅型12.78Å.模拟时,石墨烯剪纸在x,y方向均未施加周期性边界条件,采用Nose-Hoover方法[22,23]进行等温调节,模拟温度控制在300 K,时间步长取1 fs,系统运动方程求解均采用速度形式的Verlet算法[24].

本文在计算原子应力时,采用位力应力(virial stress),其定义如下[25]:

其中α和β代表笛卡尔坐标系下各矢量在不同方向(x,y,z)的分量,Si代表i原子的原子应力,V为系统的总体积,m(i)为i原子的质量,v(i)为i原子的速度,j为i原子的邻接原子,r(i)和r(j)分别表示i原子和j原子的位置矢量,f(ij)为邻接原子j作用于i原子的力矢量.位力应力实际上是描述所观察的空间区域动量变化的张量,包含区域内原子流入流出和原子间作用力改变引入的影响,故位力应力由两部分组成,(6)式右边第一部分为动能贡献项,第二部分为势能贡献项.具体讨论详见文献[26].

3 结果与讨论

3.1 石墨烯剪纸的拉伸应力应变响应规律

图2给出了典型的单层和双层石墨烯剪纸及完美石墨烯拉伸应力应变曲线.需要指出的是,由于石墨烯薄膜是由单层碳原子构成,其厚度必须采用连续介质假设后计算应力才有意义.本文在计算应力时,单层石墨烯薄膜的有效厚度取石墨晶体的层间距0.335 nm,双层石墨烯的有效厚度为0.67 nm[4,5].

图2中插图为与石墨烯剪纸相同尺寸的完美石墨烯的拉伸应力应变曲线,本文得到的单层锯齿型完美石墨烯的强度为108.9 GPa,断裂应变为0.214,计算结果与文献[4]的实验结果和文献[5,6]等的计算结果一致.本文得到的双层AB型完美石墨烯的杨氏模量为893.5 GPa,强度为90.9 GPa,断裂应变为0.173,计算结果与文献[27]的报道结果一致.

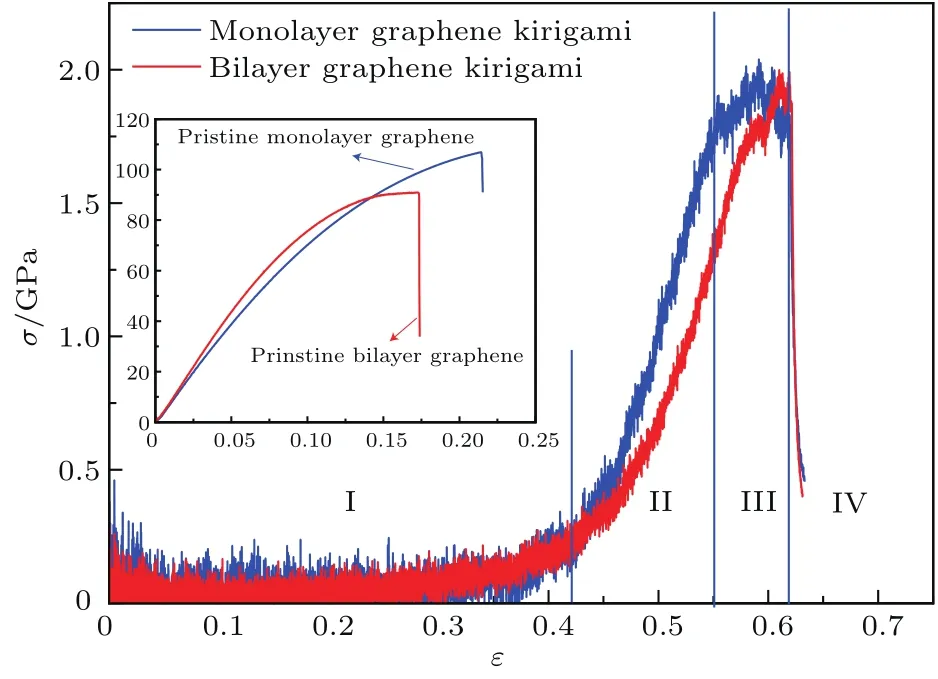
图2 (网刊彩色)单层和双层石墨烯剪纸及完美石墨烯拉伸应力应变曲线Fig.2. (color on line)Stress-strain cu rves of the m onolayer,bilayer graphene kirigam i and p rinstine graphene.

由图2可知,无论单层石墨烯剪纸还是双层石墨烯剪纸,其拉伸应力应变响应与完美石墨烯的不同,石墨烯剪纸表现出明显的大变形力学行为特征,其可承受的应变可达到完美石墨烯的3倍.双层石墨烯剪纸的应力应变响应规律与单层石墨烯剪纸的相似.

以单层石墨烯剪纸为例,其应力应变曲线大致可以分成四个阶段,如图2所示,分别为:面外变形阶段、弹性变形阶段、屈服变形阶段和断裂阶段.在第一个阶段,石墨烯剪纸的应力并未随应变的增加而明显增加,基本保持不变.结合图3(b)的原子构型图可知,在该阶段,石墨烯剪纸发生了明显的面外变形,而石墨烯剪纸中六边形碳环并未发生明显变化.由此可知,在该阶段C—C键并未发生明显的弹性伸长,因此应力并未随应变明显增加,当应变达到0.42时,应力达到0.3 GPa.由此阶段可知,石墨烯剪纸在该阶段所承担的应变已经达到完美石墨烯的近两倍.在第二阶段,石墨烯剪纸的应力随应变的增加基本呈线性增加,其斜率即石墨烯剪纸的杨氏模量为12.6 GPa.由图3(c)的原子构型图可以发现,在该阶段,石墨烯剪纸中面外变形已经结束,但六边形碳环发生了明显的变形,正六边形变得不规则.结合应力随应变增加的现象,说明在该阶段C—C键发生了弹性伸长.在第三阶段,石墨烯剪纸的应力随着应变的增加变化不明显,说明石墨烯剪纸进入屈服阶段,应力达到1.8 GPa左右.由图3(d)的原子构型图可以发现,在该阶段,石墨烯剪纸中的C—C键开始出现断裂现象.我们还发现,C—C键的断裂最初出现在石墨烯剪纸的切口或边缘附近,说明该位置产生了应力集中,此现象可由图4的原子应力分布证实.当应变继续增加,达到0.62时,整个石墨烯剪纸断裂.以上第二阶段至第四阶段,石墨烯所承担的总应变约为0.2,与完美石墨烯的相当,由此可以推断面外变形是石墨烯剪纸产生大变形力学行为的主要原因.

对于双层石墨烯剪纸,考察其拉伸破坏过程,发现与单层石墨烯剪纸的基本相似.图5为双层石墨烯剪纸在断裂前的原子构型及应力分布图.由图5可知,双层石墨烯在受到拉伸载荷时也产生了较大的离面变形.结合其原子应力分布,发现在双层石墨烯剪纸的切口边缘附近也产生了应力集中现象,C—C键在这些位置首先断裂.

由以上分析可知,单层石墨烯剪纸和双层石墨烯剪纸具有相同的拉伸应力应变响应规律和变化破坏机制,可承担的应变均可达到完美石墨烯的3倍,其中面外变形是石墨烯剪纸产生大变形力学行为的主要原因.

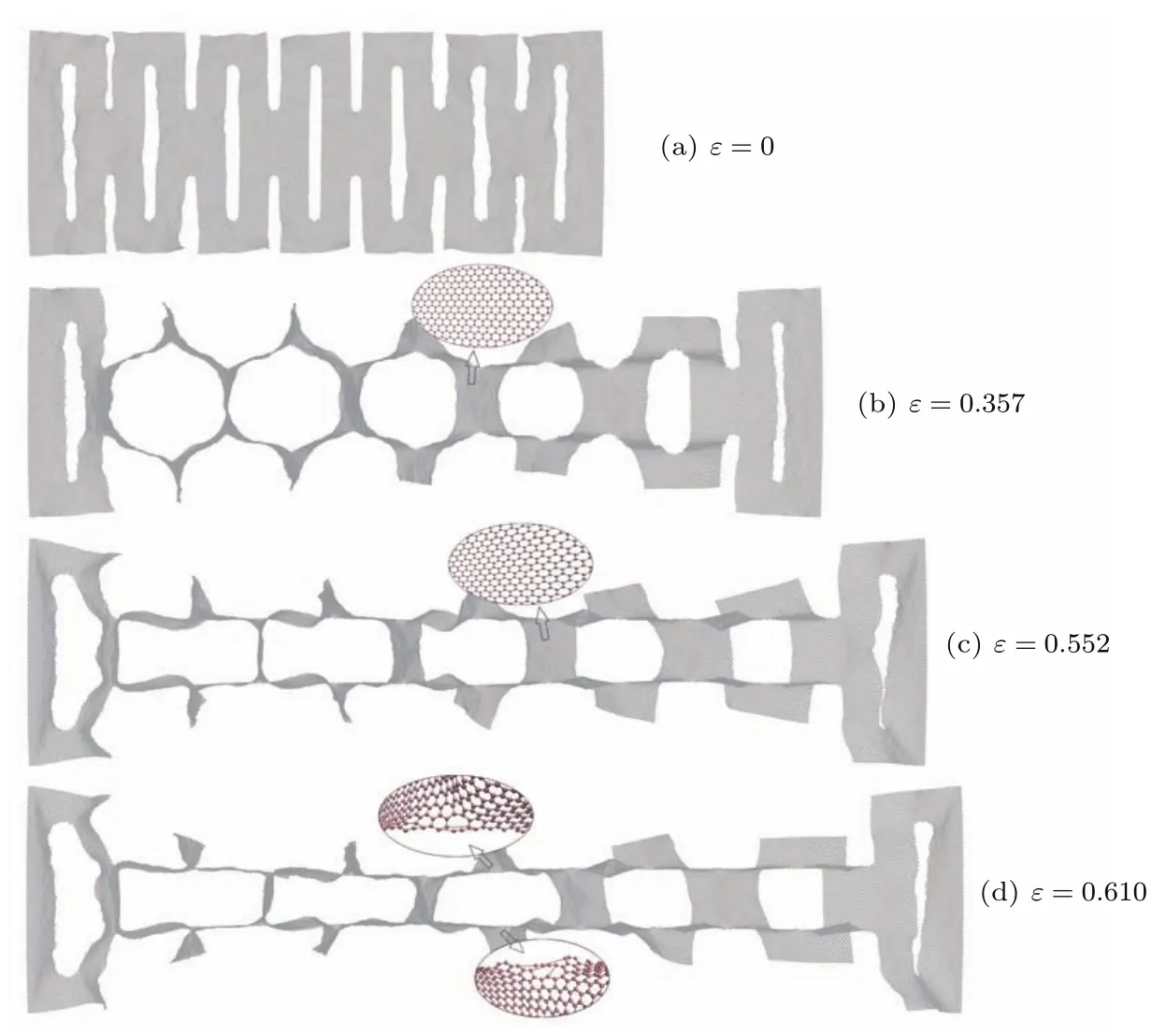
图3 (网刊彩色)锯齿型石墨烯剪纸的不同变形阶段的原子构型Fig.3.(color on line)Snapshots of the top view of the atom con figurations of the zigzag m onolayer graphene kirigam i.

图4 (网刊彩色)单层锯齿型石墨烯剪纸在断裂前的原子应力分布(ε=0.607)Fig.4.(color on line)Stress d istribution of m onolayer zigzag graphene kirigam i p rior to the failure (ε=0.607),where the data are scaled between 0 and 1.

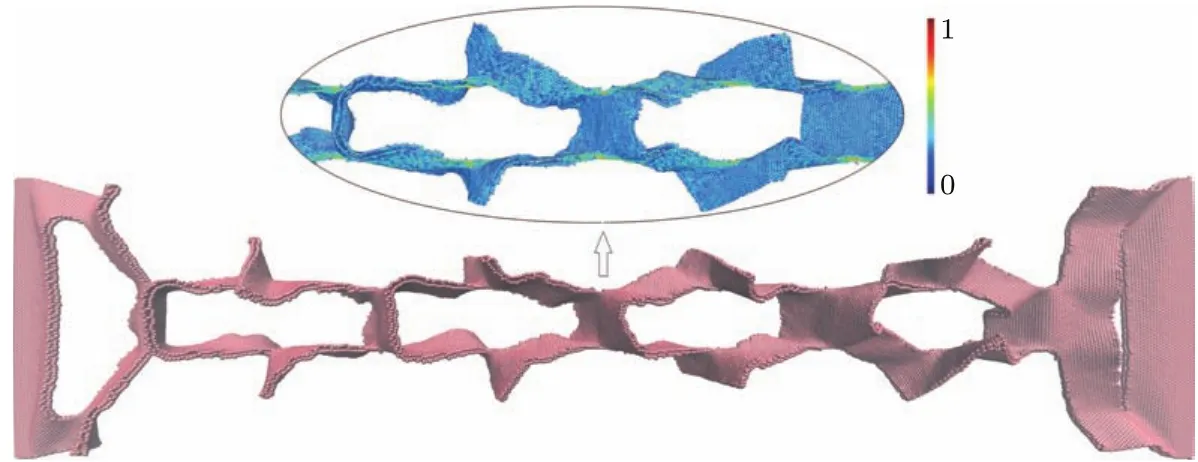
图5 (网刊彩色)双层石墨烯剪纸在断裂前的原子构型及应力分布(ε=0.614)Fig.5.(color on line)Snapshots of the top view of the atom con figurations and stress distribution of bilayer graphene kirigam i p rior to the failu re(ε=0.614),where the data are scaled between 0 and 1.

3.2 切口几何参数对石墨烯剪纸力学性能的影响

石墨烯剪纸的力学性能依赖于切口图案的形状和尺寸等因素.为了研究切口几何参数对石墨烯剪纸力学性能和力学行为的影响,结合图1,在文献[15]研究的基础上,定义了以下3个无量纲几何参数:

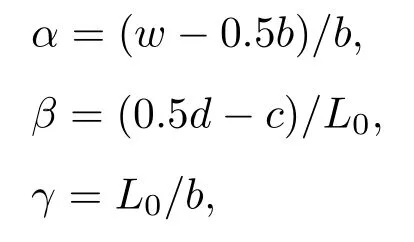
其中,α为内外切口重合部分的宽度(w−0.5b)与石墨烯剪纸宽度(b)的比值,其理论变化范围为−0.5—0.5,可以通过改变切口高度w实现,为垂直于拉伸方向的一个参数,可以描述切口所占整个石墨烯的比例,α越大,切口高度越大,内外切口重合部分越多;β为内外切口重合部分的长度(0.5d−c)与石墨烯剪纸长度(L0)的比值,为使石墨烯剪纸保持较稳定结构,该参数的取值范围约为0.01—0.10,可以通过改变切口重复单元的宽度d实现,为平行于拉伸方向的一个参数,可以描述切口的密度,β越大,切口重复单元的数量越少,切口密度越小;而γ为石墨烯剪纸的长宽比,描述具有相同α和β的石墨烯剪纸的尺寸效应.

图6为不同几何参数α的扶手椅型石墨烯剪纸的应力应变曲线,由图6可知,几何参数α(或切口高度w)对石墨烯剪纸的应力应变响应有明显的影响.当α＜0时,随着参数α的增加,应力应变曲线中并没有明显的如图2所示的面外变形阶段(阶段I),石墨烯剪纸的拉伸强度急剧降低,断裂应变较小.而当α＞0后,随着α的增加,应力应变曲线中出现了明显的面外变形阶段(阶段I),拉伸强度基本保持不变,趋于一个常数,约为3 GPa,而断裂应变明显增加.以上拉伸强度和断裂应变随几何参数α的变化趋势也可以由图7看出.图7中(包括后续图8和图9中)的拉伸强度和断裂应变均为分别除以相同尺寸的完美石墨烯之后的结果,由此可以直接量化考察几何参数的影响.

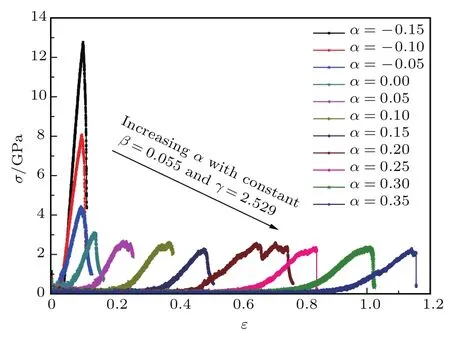
图6 (网刊彩色)不同几何参数α的扶手椅型单层石墨烯剪纸的应力应变曲线Fig.6.(color on line)Stress-strain cu rves for m onolayer arm chair kirigam i sheets keeping constantβ= 0.055,γ=2.529 and varyingα.

由图7可以看出,无论对于扶手椅型还是锯齿型石墨烯剪纸,当α＜0时,随着参数α的增加,拉伸强度基本上呈线性降低,而断裂应变对α不敏感,基本保持不变,其值甚至低于完美石墨烯的断裂应变,约为完美石墨烯的70%—80%.而当α＞0后,随着α的增加,拉伸强度基本保持不变,趋于一个常数,而断裂应变明显增加,其值约为完美石墨烯断裂应变的5—6倍.

以上的变化规律可以由不同几何参数α的石墨烯剪纸的不同变形破坏机制得以解释和理解.当α=0时,结合图1可知,石墨烯剪纸内外切口刚好重合.当α＜0时,内外切口无重合部分,在这种情况下,石墨烯剪纸难以产生面外变形,α越小,产生面外变形的概率就越小.因此,断裂应变没有提高,却低于完美石墨烯的断裂应变,此时,切口可以看作是石墨烯中的线(裂纹)缺陷,缺陷的存在降低了石墨烯的强度和断裂应变.而当α＞0时,内外切口有重合部分,在拉伸载荷的作用下,石墨烯剪纸更易于发生面外变形,在这种情况下,石墨烯剪纸的延展性得到大幅提高.

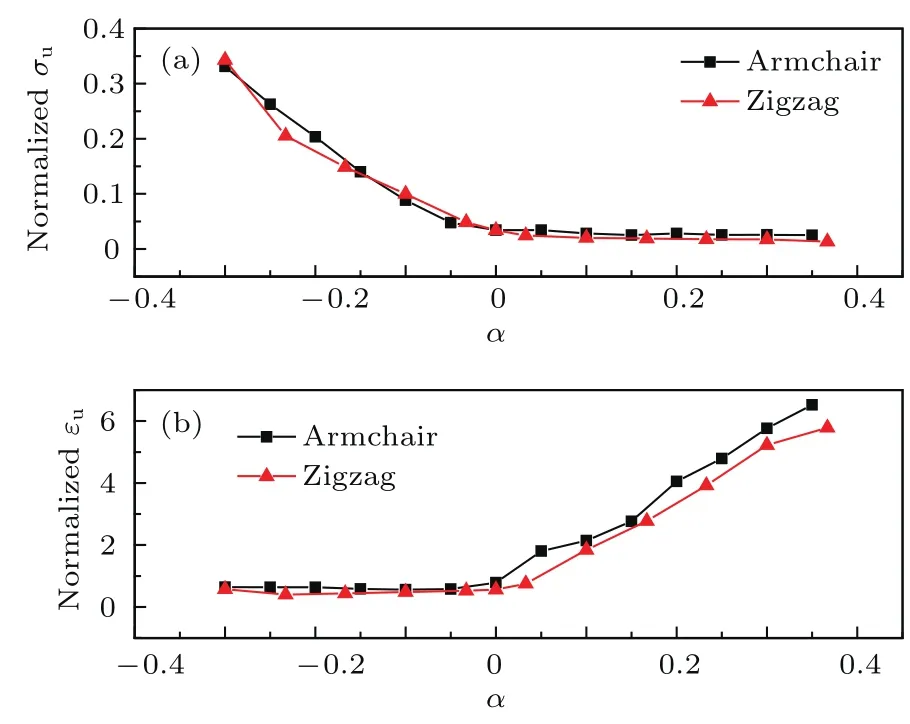
图7 (网刊彩色)不同几何参数α对单层石墨烯剪纸的(a)拉伸极限强度和(b)断裂应变的影响规律,其中,对于扶手椅型石墨烯剪纸,β=0.055,γ=2.529;对于锯齿型石墨烯剪纸,β=0.055,γ=2.444Fig.7.(color on line)E ff ects ofαon the(a)tensile u ltim ate strength and(b)fracture strain ofm onolayer graphene kirigam i for constantβandγ.For armchairβ=0.055,γ=2.529,and for zigzagβ=0.055, γ=2.444.Data are norm alized by p ristine graphene resu lts w ith the sam e size.

图8给出了不同几何参数β对石墨烯剪纸的拉伸强度和断裂应变的影响规律.由图8可看出,无论扶手椅型还是锯齿型石墨烯剪纸,其拉伸强度随几何参数β的增加而增加,而断裂应变随β的增加而降低.导致以上规律的原因依然可从石墨烯剪纸的变形破坏机制加以解释和理解.几何参数β越大,表示在石墨烯剪纸中,重复单元的个数越少,切口所占比例越少,发生面外变形的概率越小,因此,导致强度增加,应变减小.需要指出的是,当β＞0.08时,石墨烯剪纸的断裂应变甚至低于完美石墨烯的断裂应变,这是因为此时切口较少,可以将其看作线(裂纹)缺陷,导致断裂应变降低.

图9给出了不同几何参数γ对石墨烯剪纸的拉伸强度和断裂应变的影响规律,由图9可知,扶手椅型和锯齿型石墨烯剪纸的拉伸强度均随长宽比参数γ的增加基本呈线性增加,而断裂应变则单调降低.而当γ＞4时,γ对拉伸强度有重要影响,而断裂应变对γ不敏感,趋于完美石墨烯的断裂应变.

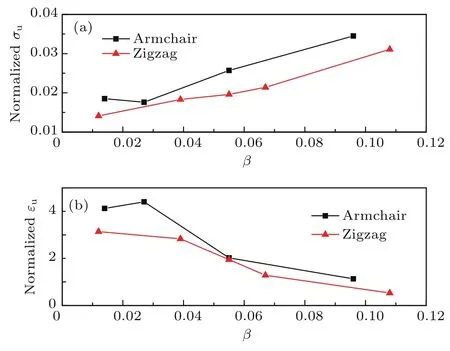
图8 (网刊彩色)不同几何参数β对单层石墨烯剪纸的(a)拉伸极限强度和(b)断裂应变的影响规律,其中,对于扶手椅型石墨烯剪纸,α=0.100,γ=2.529;对于锯齿型石墨烯剪纸,α=0.100,γ=2.444Fig.8.(color on line)E ff ects ofβon the(a)tensile u ltim ate strength and(b)fracture strain ofm onolayer graphene kirigam i for constantαandγ.For armchairα=0.100,γ=2.529,and for zigzagα=0.100, γ=2.444.Data are norm alized by p ristine graphene resu lts w ith the sam e size.

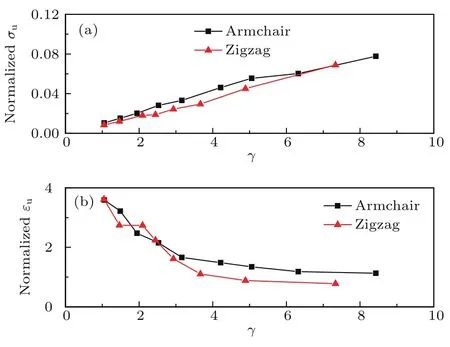
图9 (网刊彩色)不同几何参数γ对单层石墨烯剪纸的(a)拉伸极限强度和(b)断裂应变的影响规律,其中,对于扶手椅型和锯齿型石墨烯剪纸,α=0.100,β=2.529Fig.9.(color on line)E ff ects ofγon the(a)tensile u ltim ate strength and(b)fracture strain ofm onolayer graphene kirigam i for constantαandβ.For arm chair and zigzag,α=0.100,β=0.055.Data are norm alized by p ristine graphene resu lts w ith the sam e size.

通过以上分析可以得出,为有效提高石墨烯剪纸的延展性,需要增加切口重合高度(增加参数α),增加重复单元数量(降低参数β),以及降低长宽比(降低参数γ).需要指出的是,由图7、图8和图9可以看出,引入合理切口后,石墨烯剪纸的剪切应变可以大幅度提高,但石墨烯剪纸的拉伸强度和弹性模量明显降低.因此,如何在不大幅度降低石墨烯强度的条件下,提高石墨烯的延展性仍是值得深入研究的课题之一.

4 结 论

本文采用分子动力学方法研究了单层与双层石墨烯剪纸的大变形拉伸力学行为和变形破坏机制,同时定义了关于剪纸切口图案的3个无量纲几何参数,系统地研究了以上参数对石墨烯剪纸的力学性能和变形破坏机制的影响规律.研究发现,通过引入规则切口,可以有效地大幅度提高石墨烯的延展性,其断裂应变可达到完美石墨烯的5—6倍,面外变形是石墨烯剪纸产生大变形力学行为的主要原因.通过控制3个几何参数,可以有效地调控石墨烯的延展性和力学行为.研究结果表明,古老的剪纸技术为提高二维纳米材料延展性、实现光电纳米器件可延展柔性化提供了一种新途径.

[1]Novoselov K S,Geim A K,M orozov SV,Jiang D,Zhang Y,Dubonos S V,G rigorieva I V,Firsov A A 2004 Science 306 666

[2]Geim A K,Novoselov K S 2007 Nat.M ater.6 183

[3]Novoselov K S,Fal’ko V I,Colombo L,Gellert P R, Schwab M G,K im K 2012 Nature 490 192

[4]Lee C,W ei X,K ysar JW,Hone J 2008 Science 321 385

[5]Zhao H,M in K,A lu ru N R 2009 Nano Lett.9 3012

[6]Pei Q X,Zhang Y W,Shenoy V B 2010 Carbon 48 898

[7]Khang D Y,Jiang H Q,Huang Y,Rogers J A 2006 Science 311 208

[8]K im D H,Ahn J H,Choi W M,K im H S,K im T H, Song J Z,Huang Y G Y,Liu Z J,Lu C,Rogers J A 2008 Science 320 507

[9]K im D H,Song J Z,ChoiW M,K im H S,K im R H,Liu Z J,Huang Y Y,Hwang K C,Zhang Y W,Rogers J A 2008 Proc.Natl.Acad.Sci.USA 105 18675

[10]Xu S,Zhang Y H,Cho J,Lee J,Huang X,Jia L,Fan J A,Su Y W,Su J,Zhang H G,Cheng H Y,Lu B W,Yu C J,Chuang C,K im T I,Song T,Shigeta K,Kang S, Dagdeviren C,Petrov I,B raun P V,Huang Y G,Paik U,Rogers J A 2013 Nat.Comm un.4 1543

[11]Song Z M,M a T,Tang R,Cheng Q,W ang X,K rishnara ju D,Panat R,Chan C K,Yu H Y,Jiang H Q 2014 Nat.Comm un.5 3140

[12]Lam oureux A,Lee K,Shlian M,Forrest S R,Shtein M 2015 Nat.Comm un.6 8092

[13]B leesM K,Barnard AW,Rose P A,Roberts SP,M cGill K L,Huang P Y,Ruyack A R,K evek JW,Kob rin B, M u ller D A,M cEuen P L 2015 Nature 524 204

[14]Hanakata P Z,Qi Z A,Cam pbell D K,Park H S 2016 Nanoscale 8 458

[15]Q i Z N,Cam pbell D K,Park H S 2014 Phys.Rev.B 90 245437

[16]Lin J H,Fang W J,Zhou W,Lup ini A R,Id robo J C, Kong J,Pennycook S J,Pantelides S T 2013 Nano Lett. 13 3262

[17]Brenner D W,Shenderova O A,Harrison J A,Stuart S J,N i B,Sinnott S B 2002 J.Phys.-Condens.M atter 14 783

[18]B renner D W 1990 Phys.Rev.B 42 9458

[19]Stuart S J,Tu tein A B,Harrison J A 2000 J.Chem. Phys.112 6472

[20]G rantab R,Shenoy V B,Ruoff R S 2010 Science 330 946

[21]Zhang P,M a L L,Fan F F,Zeng Z,Peng C,Loya P E, Liu Z,Gong Y J,Zhang J N,Zhang X X,A jayan P M, Zhu T,Lou J 2014 Nat.Comm un.5 3782

[22]Hoover W G 1985 Phys.Rev.A 31 1695

[23]Nose S 1984 M o l.Phys.52 255

[24]Swope W C,Andersen H C,Berens P H,W ilson K R 1982 J.Chem.Phys.76 637

[25]Subram aniyan A K,Sun C T 2008 Int.J.Solids.Struct. 45 4340

[26]Zhao Y P 2014 Nano and M esoscopic M echanics(Beijing:Science Press)p14(in Chinese)[赵亚溥2014纳米与介观力学(北京:科学出版社)第14页]

[27]Zhang Y Y,W ang C M,Cheng Y,X iang Y 2011 Carbon 49 4511

PACS:62.23.Kn,61.48.Gh,62.25.–g,31.15.xvDOI:10.7498/aps.66.066201

Investigation on the large tensile deform ation and m echan ical behaviors of graphene kirigam i∗

Han Tong-Wei†Li Pan-Pan

(Facu lty of Civil Engineering and M echanics,Jiangsu University,Zhenjiang 212013,China)
(Received 13 October 2016;revised m anuscrip t received 8 Novem ber 2016)

One of the m ain challenges in developing future stretchable nanoelectronics is the m ism atch between the hard inorganic sem iconductorm aterials and the ductility requirem ents in the app lications.This paper show s how the kirigam i architecturalapproach,inspired by the ancient Japanese art of cutting and folding paper app lied onmacroscale,m ight be an eff ective strategy to overcom e thism ism atch on nanoscale.In thiswork,the tensile large deform ation and m echanical behaviors of arm chair and zigzag graphene kirigam i w ith rectangles and half circles cutting patterns are investigated based on classical molecular dynam ics simulations.The eff ects of three non-dimensional geometric parameters that control the cutting patterns on the m echanics and ductility of graphene kirigam i are also studied system atically.The resu lts indicate that the enhancement in fracture strain can reach more than five times the fracture strain of pristine graphene.The defined three param eters can be ad justed to tailor or m anipu late the ductility and m echanical behaviors of graphene.These results suggest that the kirigam iarchitectural approach m ay be a suitable technique to design superductile two-dimensional nanomaterials and potentially expand their app lications to other strain-engineered nanodevices and nanoelectronics.

graphene,kirigam i,large deformation,molecular dynam ics

10.7498/aps.66.066201

∗江苏省自然科学基金(批准号:BK 2011490)资助的课题.

†通信作者.E-m ail:twhan@u js.edu.cn

*Pro ject supported by the Natural Science Foundation of Jiangsu Province,China(G rant No.BK 2011490).

†Corresponding author.E-m ail:twhan@u js.edu.cn