一种编码式宽带多功能反射屏∗

陈巍 高军†张广 曹祥玉‡杨欢欢 郑月军

1)(空军工程大学信息与导航学院,西安 710077)

2)(驻765厂军事代表室,宝鸡 721006)

(2016年9月17日收到;2016年11月1日收到修改稿)

一种编码式宽带多功能反射屏∗

陈巍1)高军1)†张广2)曹祥玉1)‡杨欢欢1)郑月军1)

1)(空军工程大学信息与导航学院,西安 710077)

2)(驻765厂军事代表室,宝鸡 721006)

(2016年9月17日收到;2016年11月1日收到修改稿)

提出了一种可控的宽带多功能反射屏.通过将射频微机电系统技术与反射屏设计相结合,首先设计了可编码式工作的单元,该单元具有工作频带宽、损耗小、控制简单的特点.由该单元基于不同编码矩阵构成的反射屏可以实现不同的功能.文中展示了多功能反射屏的极化旋转和捷变散射场性能.仿真结果表明:设计的反射屏在8.9—13.2 GHz频段范围内极化转化率高达90%以上,且在8.9—13.1 GHz频段范围内可实现10 dB以上的雷达散射截面减缩.实测结果与仿真结果基本一致.

编码,宽带,极化旋转,低雷达散射截面

1 引 言

超材料是由人工微结构周期排列构成的新型电磁媒质[1,2].相比于天然材料,超材料可以实现许多超常规的电磁特性,如负折射、同相反射、完美吸收等[3−8],这使其在许多领域都表现出日新月异的应用前景.近年来,随着电子对抗技术的不断发展,雷达隐身技术受到越来越多的重视.而超材料的研究为解决雷达隐身中的难题提供了一条新的技术途径.

雷达隐身的目标就是改变雷达回波信号特征,减小物体被雷达探测的概率.雷达散射截面(radar cross section,RCS)是表征物体雷达隐身性能的主要指标[9−12].现有利用超材料减缩RCS的方法有很多[13−17],总结起来大致可分为3种.一是改变雷达回波的极化特征,使回波信号转变为正交极化波,从而实现正交极化隐身.如文献[13]中设计了一种极化旋转反射表面,反射波可在5.98—18.84 GHz频带内实现50%以上的极化转换.这种方法对于单极化工作的雷达可实现有效隐身,但并不能很好地应对双极化工作雷达的探测.利用超材料的吸波特性来减少雷达回波的幅值,是超材料应用于减缩RCS的第二种思路.在文献[14]中, Landy等提出利用超材料的强谐振特性可以实现几乎完美吸收电磁波的吸波体.与常见的吸波材料相比,其最突出的优点在于厚度极薄(仅为1/100波长[15]),研究人员随后提出该吸波体可以应用于物体的隐身设计,并成功展示了良好的RCS减缩效果.需要指出的是,强谐振导致的窄带工作特性也在一定程度上限制了其推广应用.超材料应用于RCS减缩的第三种方法是基于波的空间叠加原理,将具有不同反射相位特性的超材料组合在一起,从而实现对散射场的控制.如文献[16]将具有180◦反射相位的理想导体和具有0◦反射相位的人工磁导体棋盘拼接,有效抑制了金属表面法线方向的RCS峰值.文献[17]将具有不同反射相位的超材料拼接在一起,实现了空间能量的漫散射分布.相比于前两种RCS减缩方法,这种基于超材料相位特性的RCS减缩方法更加灵活,且散射场可控,其应用前景非常广阔.但目前的研究大多仍是针对性能固定的反射屏.尤其是随着新一代捷变雷达技术的发展,性能单一、工作带宽窄等问题极大地限制了这些反射屏的应用.

2014 年,Cui等[18]提出了编码超材料的概念,并成功展示了针对相位编码的超材料.这种编码的概念不仅丰富了超材料的描述方式,也为实现功能多样、可智能工作的超材料提供了一条有效途径.针对常见超材料频带窄、性能单一的问题,本文将新型微机电系统(m icro-electromechanical system, MEMS)技术与槽线结构的场分布特点相结合,并基于编码概念,设计了一种可控的宽带多功能反射屏.理论仿真和实际测试结果均表明:在8.5—13.5 GHz,该反射屏可动态调整散射雷达波的极化或波束形状,这使其在智能隐身应用中具有非常广阔的前景.

2 编码式反射单元及工作原理

本文提出的编码式反射型单元结构如图1(a)所示.介质上表面印刷有方形金属贴片,下表面是刻蚀准十字形缝隙的金属层,金属层的下方为完整的金属底板,两者中间由厚2.8 mm的空气层隔开.如图1(b),为了获得动态可调的反射特性,缝隙上对称地集成两个射频MEMS开关.优化后的结构参数为:p=12 mm,a=6 mm,h1=2 mm, h2=2.8mm,l=11.2mm,w=0.34mm.介质材料为厚2mm的聚四氟乙烯,介电常数2.65,损耗角正切0.001.

本文采用的射频MEMS开关,其实物放大示于图2(a),相比于常用的PIN二极管开关,它具有插入损耗小、功耗低、尺寸小等优点[19,20].仿真中,采用图2(b)和图2(c)所示的两种结构模拟其导通和断开的两种工作状态.对于图1所示的单元,工作时,控制两个MEMS开关交替地处于导通或截止状态,对应的两种单元特性可以用“0”或“1”表示.为了具体说明单元的工作原理,图3给出了当平面波沿+y方向入射时单元在两种工作状态下的电场分布.如图3(a),对于“0”状态,MEMS1导通,MEMS2断开,根据槽线的结构特点,此时反射波电场沿−x方向;同理,对于“1”状态,反射波电场沿+x方向.综上可知,在同一入射波照射情况下,从极化方面来看,所提单元通过射频MEMS开关实现了对反射波极化方向的控制;而就相位方面而言,所提单元两种工作状态的反射波相位相差180◦.

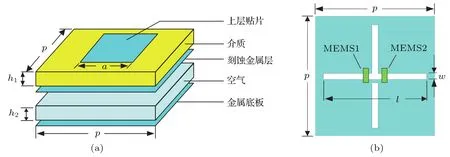
图1 (网刊彩色)编码式反射单元 (a)三维结构;(b)集成有MEMS开关的刻蚀金属层Fig.1.(color on line)Coding refl ective unit cell:(a)Tree-d im ensional structure of unit cell;(b)m etal layer integrated w ith MEM S sw itch.

图2 (网刊彩色)MEMS (a)实物图;(b)MEMS导通;(c)M EMS截止Fig.2.(color on line)MEMS:(a)Photograph of MEMS;(b)MEMS operation state is in“ON”;(c)MEMS operation state is in“OFF”.

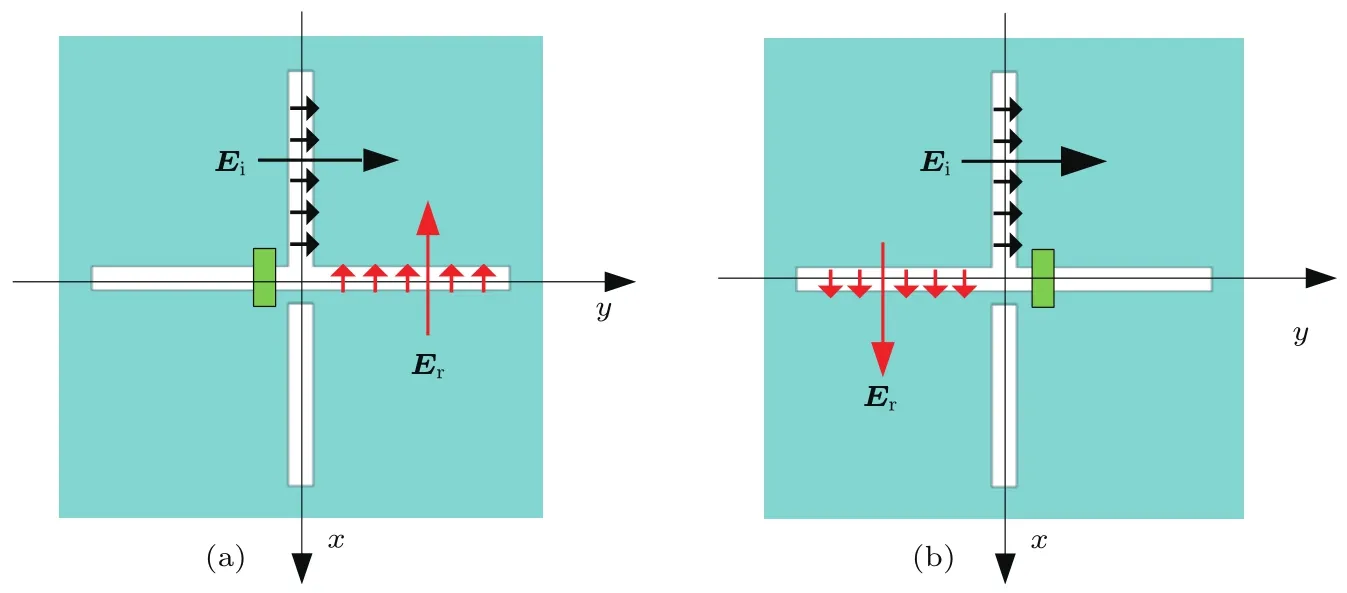
图3 (网刊彩色)两种工作状态下单元的电场分布 (a)“0”状态;(b)“1”状态Fig.3.(color on line)E lectric-field d istribu tion of the unit cell under two operation states:(a)“0”state;(b)“1”state.

3 编码式多功能反射屏仿真分析

3.1 极化旋转反射屏

采用Ansoft HFSS 14.0对图1所示的单元结构进行仿真.利用Floquet端口和周期性边界模拟无限大阵列.定义rxx=|Erx/Eix|,rxy= |Ery/Eix|,ryx=|Erx/Eiy|,ryy=|Ery/Eiy|分别表示x到x极化、x到y极化、y到x极化、y到 y极化的反射系数.其中下标i,r分别表示入射波和反射波.则x到y的极化转化率可表示为PCR=r2xy/(r2xx+r2xy)[21].图4给出了“0”,“1”单元的极化转化率和反射相位.可以看到,在8.9—13.2 GHz,“0”和“1”单元的交叉极化反射系数基本大于0.948,10.1GHz频域附近最低为0.941.极化转化率基本大于0.9,且两单元的交叉极化反射相位差为180◦,同极化反射相位基本相同.

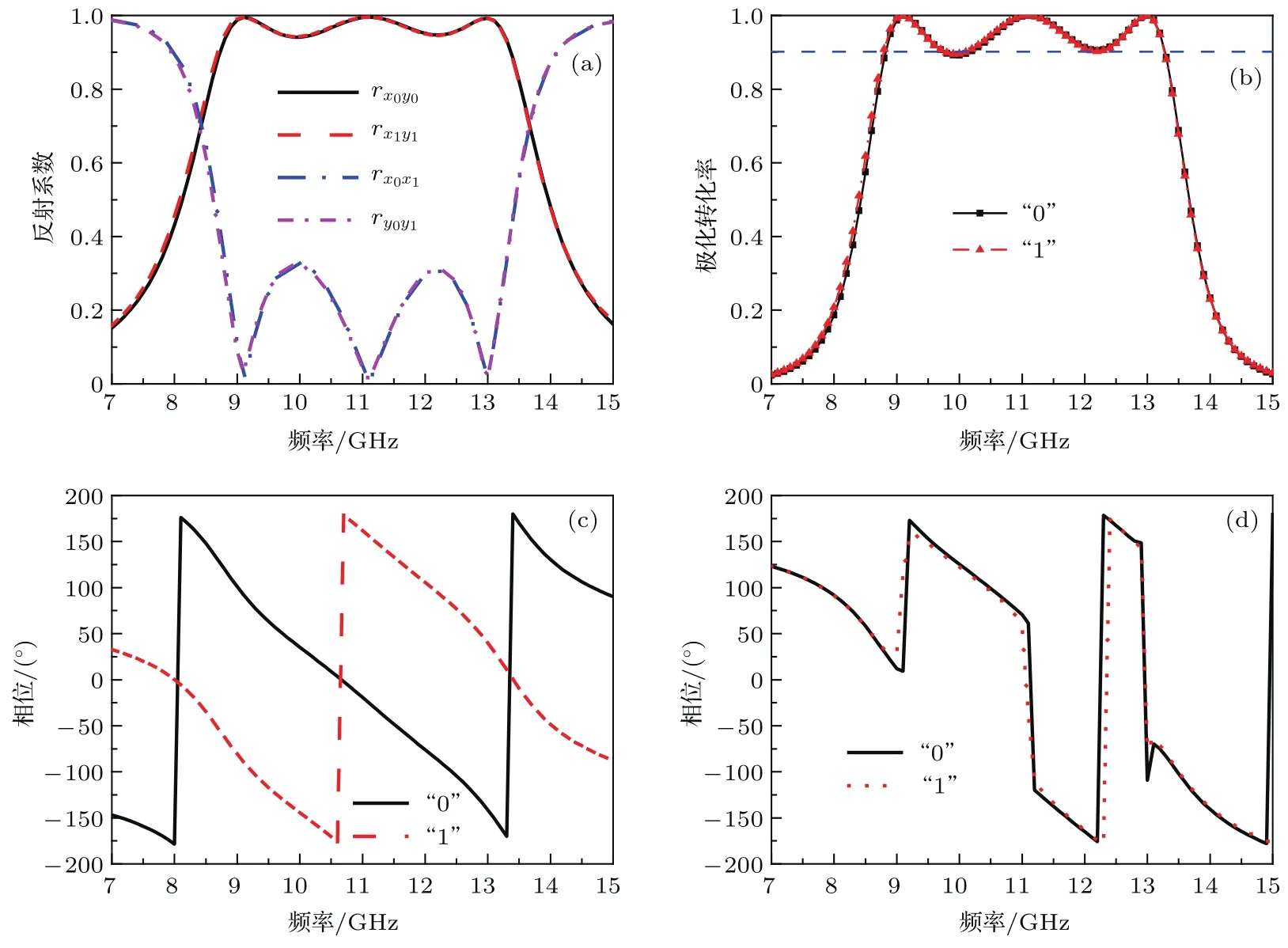
图4 (网刊彩色)周期单元仿真结果 (a)反射系数;(b)极化转化率;(c)交叉极化反射相位;(d)同极化反射相位Fig.4.(color on line)Sim u lation resu lts of period ic unit cell:(a)Refl ection coeffi cient;(b)polarization conversion ratio;(c)cross-polarization refl ection phase;(d)co-polarization refl ection phase.

3.2 低RCS反射屏

利用单元“0”,“1”工作状态的交叉极化反射相位差为180◦的特点,结合不同的编码组合,可以实现不同散射波束形状的超表面.为了抑制普通金属板的法向强散射,本文提出两种排布方式验证反射屏的功能.

3.2.1 棋盘式低RCS反射屏

图5给出了棋盘式低RCS反射屏的结构示意图.其总反射场可表示为

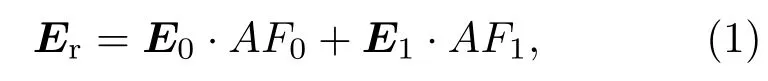
(1)式中AF0,AF1分别表示单元“0”和单元“1”的阵因子[6].不妨假设棋盘结构总面积为1,那么对于2×2元阵列,AF0,AF1可以表示为

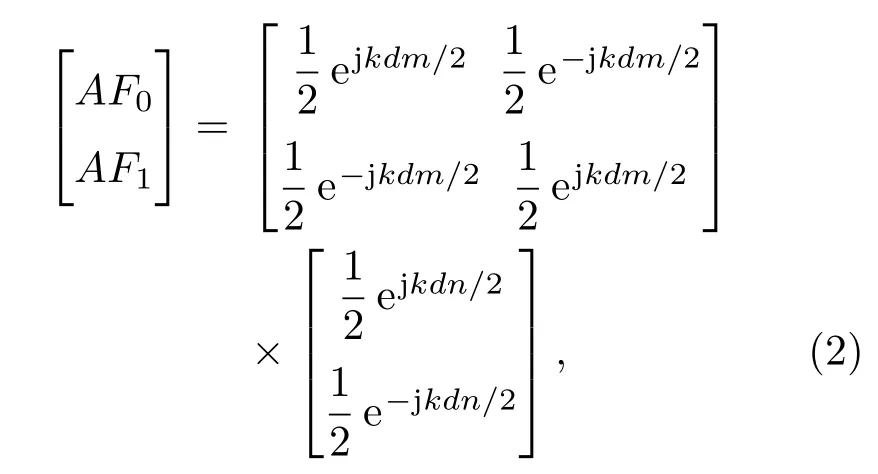
其中,m=sinθcosφ,n=sinθsinφ,θ和φ分别为入射波与z轴和x轴的夹角,k=2π/λ,d为单元“0”和单元“1”的中心间距.当电磁波垂直入射时,即θ=0◦,φ=0◦,有AF0=AF1=1/2.

E0和E1分别代表单元“0”和单元“1”的反射场.与文献[17]中单元反射幅度为1不同的是,所设计的编码式单元具有极化旋转特性,反射场幅度与极化反射系数有关.因此,对于垂直入射场Ei,当入射波极化沿x方向时,反射场E0和E1可分别展开为

对于由所提单元组成的棋盘式反射屏,根据图4的仿真结果,单元工作在“0”,“1”状态的同极化、交叉极化反射系数分别相等,交叉极化反射相位相差180◦,同极化反射相位一致.因此,其反射场为

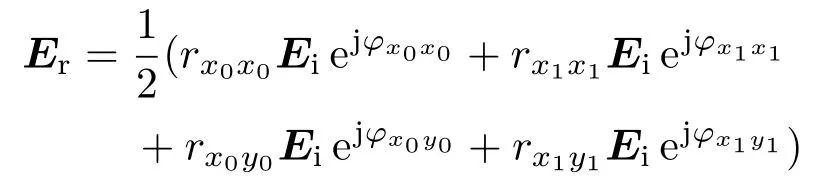
即棋盘式反射屏的反射场大小为|Er|=rxx|Ei|.而对于理想的金属平板,同极化反射系数为1,交叉极化反射系数为0,所以金属平板反射场大小为为确保棋盘式反射屏与金属平板相比,RCS减缩量达10 dB以上,则必须满足

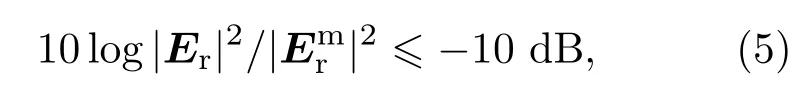
将金属平板与棋盘式反射屏的反射场代入(5)式,进一步推导可得

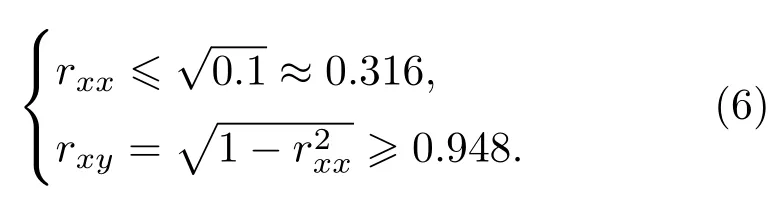
当入射波极化沿y方向时,推导过程与x极化波相似,结论相同.需要指出的是(6)式仅适用于棋盘式低RCS反射屏法线方向的RCS减缩.

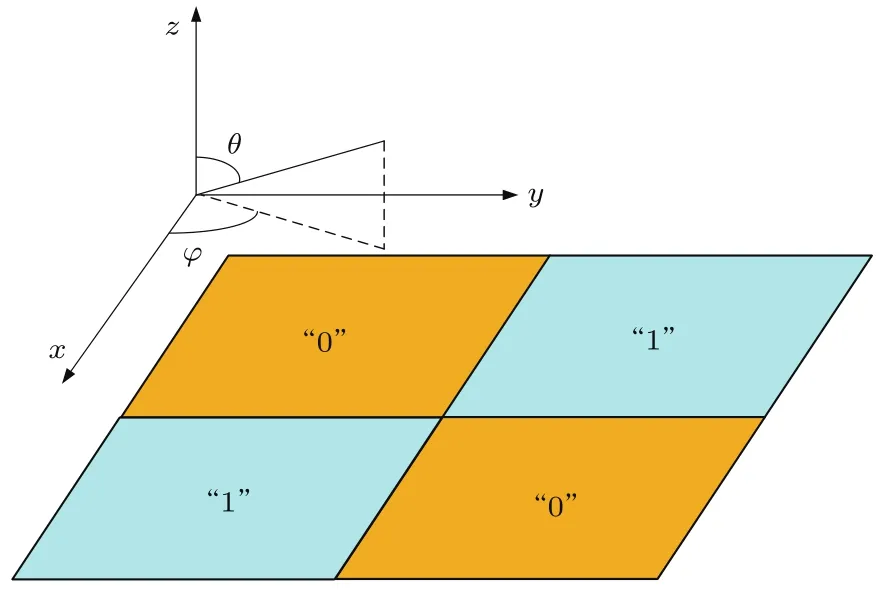
图5 (网刊彩色)棋盘结构示意图Fig.5.(color online)chessboard structure.

为验证上述推导,对24×24单元构成的反射屏进行仿真,每4个单元构成一个元胞,以确保一定的周期性,并用一个“0”或“1”表示,则整个反射屏的编码矩阵如图6(a)所示.图6(b)给出了仿真得到的反射屏法线方向的RCS减缩量,可以看到,棋盘式编码反射屏对不同极化入射波的RCS减缩效果相同,且在8.9—13.1 GHz频段范围内,反射屏的RCS较同样大小的金属板几乎都有10 dB以上减缩量,在10.1 GHz附近RCS减缩值最小约为9.2 dB,这是因为在10.1 GHz频域附近两单元的交叉极化反射系数约为0.941,小于0.948.这一结果表明(6)式的结论和图4(a)的仿真结果一致,从而证实了理论推导.

图6 (网刊彩色)棋盘式编码反射屏仿真 (a)棋盘编码矩阵;(b)法向RCS减缩量;(c)金属平板在11 GHz处双站RCS三维图;(d)棋盘反射屏在11 GHz处双站RCS三维图Fig.6.(color on line)Sim u lation of chessboard cod ing refl ective su rface:(a)Chessboard cod ing m atrix; (b)RCS reduction for norm ally incident waves;(c)three-d im ensional bistatic RCS of the m etal p lane at 11 GHz;(d)th ree-d im ensional bistatic RCS of the chessboard cod ing refl ective su rface at 11 GHz.

3.2.2 随机分布低RCS反射屏

对比图6(c)与图6(d)中同等尺寸金属平板与棋盘式反射屏的双站散射方向图可以发现,RCS在反射屏法线方向上有明显减缩,但在四个对角线方向出现了明显的峰值.为了减小反射屏被双站雷达探测的可能性,应使散射能量在整个空间尽可能平均分布.为此,采用遗传算法[22]对反射屏的编码矩阵进行优化,目标函数设定为使整个空间散射场的最大值最小化[22],优化后得到了图7(a)所示的随机编码矩阵.图7(b)给出了相同尺寸下金属平板及随机编码反射屏的法向单站RCS对比.与棋盘式编码反射屏不同,该反射屏对不同极化入射波的RCS减缩效果略有不同,分析认为其原因是随机编码矩阵不对称.图7(c)给出的是11 GHz处随机编码反射屏的散射方向图,图7(d)对比了随机编码反射屏与金属平板以及棋盘式编码反射屏在11 GHz处φ=45◦平面的双站RCS.显然,相比于棋盘式编码设计,反射屏对角线方向上的强散射能量经随机优化编码后得到有效的抑制,整个空间能量分配更加均匀.上述结果验证了设计反射屏的宽带RCS减缩效果及散射场的动态可调特性.

4 实测验证与分析

为证实可控反射屏的多功能特性,实际制作了4个固定的反射屏样品,每个样品均含有24×24个单元,其对应的编码矩阵分别为全“0”编码,全“1”编码及图6(a)和图7(a)所示的棋盘编码和随机编码.在微波暗室中,利用空间波法[23]对4个样品分别进行测试.图8给出了反射屏样品实物及实测配置,利用一个标准喇叭天线发射电磁波,另一个标准喇叭天线接收经反射屏反射的电磁波,两个喇叭天线分别连接到Agilent N5230C矢量网络分析仪的两个端口.极化测试中,其中一个喇叭为垂直极化,另一个为水平极化,而RCS测试时,两个喇叭保持同极化.

图7 (网刊彩色)随机编码反射屏仿真 (a)随机编码矩阵;(b)法向单站RCS对比;(c)11 GHz处双站RCS三维图;(d)11 GHz处φ=45◦平面双站RCS对比Fig.7.(color on line)Sim u lation of random coding refl ective su rface:(a)Random cod ing m atrix;(b)m onostatic RCS com parison for norm ally incidentwaves;(c)three-d im ensionalbistatic RCS at 11 GHz;(d)bistatic RCS com parison ofφ=45◦p lane at 11 GHz.

图8 (网刊彩色)实物制作及测试 (a)反射屏样品实物图;(b)实测配置Fig.8.(color on line)Prototype fabrication and m easu rem ent:(a)Photograph of the refl ective surface p rototype;(b)m easu rem ent setup.

图9对比给出了仿真与实测的结果.从图9(a)给出的极化转化率结果可以看到,测试与仿真整体趋势一致,实测的转化率较仿真略偏低.分析认为,造成这一偏差的主要因素有制作中样品的不平整度较大、测试时照射波与样品之间并非理想垂直等.图9(b)为仿真和测试的棋盘编码及随机编码反射屏在法线上的RCS减缩量.值得一提的是,由于棋盘编码的设计目标是使反射屏在法线上散射场最小,而随机编码的目标则在于使反射屏在整个空域的散射能量分布更均匀,因此,前者在法线上的RCS减缩效果要好于后者,这与图9(b)的结果相一致;此外,从图9(b)还可以看出,仿真与测试的RCS减缩在量值上符合较好,但测试结果相比与仿真结果产生了频率偏移.通过分析,认为导致两者之间频偏的因素包括:样品的不平整性、加工误差及系统误差等.综上所述,图9(a)和图9(b)给出的极化旋转和RCS减缩结果,进一步证实了提出的编码式反射屏在宽频带内工作特性可动态调控.

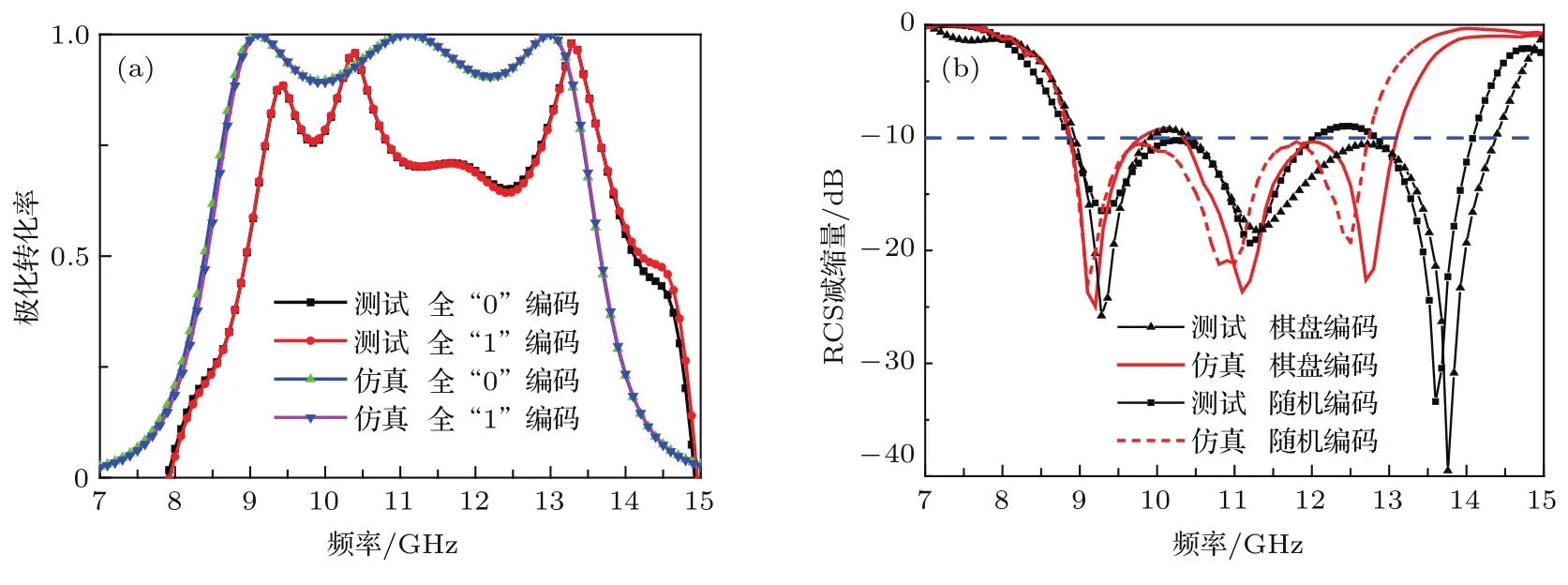
图9 (网刊彩色)实测结果与仿真结果对比 (a)极化转化率;(b)RCS减缩量Fig.9.(color on line)Com parison of the m easurem ent and sim u lation resu lts:(a)Polarization conversion ratio;(b)RCS reduction.

5 结 论

本文结合射频MEMS技术提出了一种宽带可控的极化旋转单元,并将该单元组成阵列,基于编码的概念,设计了一种多功能反射屏.所提出的单元中集成两个MEMS开关,通过控制开关的工作状态,该单元可在8.5—13.5 GHz频带内控制反射波的极化状态.将单元组成反射屏后,利用其极化可控特性,结合单元编码,实现反射屏的散射捷变.本文分析了所提单元结构的工作原理,理论推导并验证了RCS减缩与极化转化率之间的关系,并仿真分析了捷变散射场特性.采用空间波法对反射屏实物进行了测试,仿真结果和实测结果都证实了编码反射屏的极化旋转和RCS减缩功能.本文基于编码概念,实现了一种宽带多功能编码反射屏,对超材料的研究具有一定的借鉴意义.

[1]Pendry J B,Schurig D,Sm ith D R 2006 Science 312 1780

[2]Lin B Q,Zhao SH,W eiW,Da X Y,Zheng Q R,Zhang H Y,Zhu M 2014 Chin.Phys.B 23 024201

[3]Zhong X Q,Cheng K,X iang A P 2013 Chin.Phys.B 22 034205

[4]Zhong M 2013 Chin.Opt.Lett.11 101601

[5]Esm aeli S H,Sedighy S H 2016 E lectron.Lett.52 70

[6]Zhao Y,Cao X Y,Gao J,Sun Y,Yang H H,Liu X,Zhou Y L,Han T,Chen W 2016 Sci.Rep.6 23896

[7]Li S J,Gao J,Cao X Y,Zhang Z,Zheng Y J,Zhang C 2015 Opt.Express 23 003523

[8]Li S J,Gao J,Cao X Y,Zhao Y,Zhang Z,Liu H X 2014 IET M icrow.An tennas Propag.9 399

[9]Liu Y,Hao Y W,Li K,Gong S X 2016 IEEE An ten. W irel.Propag.Lett.15 1028

[10]Liu Y,Li K,Jia Y T,Hao Y W,Gong S X,Jay-Guo Y 2016 IEEE Trans.An tennas Propag.64 326

[11]Edalati A,Saraband K 2014 IEEE Trans.An tennas Propag.62 747

[12]Su P,Zhao Y J,Jia S L,ShiW W,Wang H L 2016 Sci. Rep.6 20387

[13]Jia Y T,Liu Y,Jay-Guo Y,Li K,Gong S X 2016 IEEE Trans.Antennas Propag.64 179

[14]Landy N I,Sa juyigbe S,M ock J J,Sm ith D R,Pad illa W J 2008 Phys.Rev.Lett.100 207402

[15]Li S J,Cao X Y,Gao J,Zheng Q R,Zhao Y,Yang Q 2013 Acta Phys.Sin.62 194101(in Chinese)[李思佳,曹祥玉,高军,郑秋容,赵一,杨群2013物理学报62 194101]

[16]Paquay M,Iriarte J C,Ederra I,Gonzalo R,M aagt P 2007 IEEE Trans.An tennas Propag.55 3630

[17]Zheng Y J,Gao J,Cao X Y,Yuan Z D,Yang H H 2015 IEEE An ten.W irel.Propag.Lett.14 1582

[18]Cui T J,Q iM Q,W ang X,Zhao J,Cheng Q 2014 Light Sci.Appl.3 218

[19]Guclu C,Perruisseau-Carrier J,Civi O A 2012 IEEE Trans.An tennas Propag.60 5451

[20]Zhen W B,Huang Q A,Li F X 2001 J.M icrowaves 17 87(in Chinese)[郑惟彬,黄庆安,李拂晓 2001微波学报17 87]

[21]Han J F,Cao X Y,Gao J,Li S J,Zhang C 2016 Acta Phys.Sin.65 044201(in Chinese)[韩江枫,曹祥玉,高军,李思佳,张晨2016物理学报65 044201]

[22]Yang H H,Cao X Y,Yang F,Gao J,Xu S H,Li M K, Chen X B,Zhao Y,Zheng Y J,Li S J 2016 Sci.Rep.6 35692

[23]Yang H H,Yang F,Xu S H,Li M K,Cao X Y,Gao J 2016 Acta Phys.Sin.65 054102(in Chinese)[杨欢欢,杨帆,许慎恒,李懋坤,曹祥玉,高军 2016物理学报 65 054102]

PACS:42.70.Qs,41.20.Jb,73.90.+fDOI:10.7498/aps.66.064203

A w ideband cod ing refl ective m etasu rface w ith m u ltip le functionalities∗

Chen Wei1)Gao Jun1)†Zhang Guang2)Cao Xiang-Yu1)‡Yang Huan-Huan1)Zheng Yue-Jun1)

1)(School of Inform ation and Navigation,A ir Force Engineering University,X i’an 710077,China)
2)(M ilitary Representative Offi ce at No.765 Factory,Baoji 721006,China)
(Received 17 Sep tem ber 2016;revised m anuscript received 1 November 2016)

A controllablew ideband mu ltifunctional reflectivemetasurface is p resented.First of all,a polarization-rotating unit cell is proposed by combingm icro-electrom echanical system(MEMS)technology w ith reflectivem etasurface design.The proposed unit cell is characterized by w ideband,low loss and controllab le p roperties.Each unit cell is integrated w ith two M EMS sw itches.W hen the two sw itches operate in diff erent states,the unit cell show s diff erent responses to p lane wave incidence,and the corresponding working states can be denoted by“0”or“1”.It isworth noting that a 180 degree reflection phase diff erence is generated for the two working states.Then,the p roposed unit cell is periodically arranged to construct a m etasurface.Based on diff erent coding m atrixes,mu ltip le functionalities can be obtained by using the proposed m etasurface.W hen all the unit cells are controlled to operate in on-or off-state,polarization-rotating function is obtained.Besides,the agility scattering field performance is also presented by using“chessboard”and“random”codings.A series of equations is derived to reveal the relationship between reflection coeffi cient of the unit cell and radar cross section(RCS)reduction of the chessboard reflective surface,which is also verified by full-wave simulations.Finally, four prototypes consisting of 576-cells,which correspond to the“all 0”,“all 1”,“chessboard”and“random”coding,are fabricated and m easured.Them easured results dem onstrate that the p roposed reflectivem etasurface shows polarizationrotating performance in a frequency range of 8.9–13.2GHz when all unit cells operate in“0”or“1”state.Themeasured resu lts of the“chessboard”and“random”coding m etasurface m anifest rem arkab le RCS reduction com pared w ith the sam e size m etal p lane.Good agreem ent between simulations and m easurem ents is obtained.Ow ing to the ability to control polarization and beam shape of the reflected wave dynam ically,the proposed reflectivemetasurface has potential app lications in the field of intelligent stealth.

coding,w ideband,polarization rotating,low radar cross section

10.7498/aps.66.064203

∗国家自然科学基金(批准号:61271100,61471389,61501494,61671464)资助的课题.

†通信作者.E-m ail:g jgj9694@163.com

‡通信作者.E-m ail:xiangyucaokdy@163.com

*Pro ject supported by the National Natu ral Science Foundation of China(G rant Nos.61271100,61471389,61501494, 61671464).

†Corresponding author.E-m ail:gjgj9694@163.com

‡Corresponding au thor.E-m ail:xiangyucaokdy@163.com