双开口Helm holtz局域共振周期结构低频带隙特性研究∗

姜久龙 姚宏杜军 赵静波 邓涛

1)(空军工程大学航空航天工程学院,西安 710038)

2)(空军工程大学理学院,西安 710051)

3)(西安飞行学院,西安 710306)

(2016年8月12日收到;2016年12月27日收到修改稿)

双开口Helm holtz局域共振周期结构低频带隙特性研究∗

姜久龙1)姚宏2)†杜军1)赵静波2)邓涛3)

1)(空军工程大学航空航天工程学院,西安 710038)

2)(空军工程大学理学院,西安 710051)

3)(西安飞行学院,西安 710306)

(2016年8月12日收到;2016年12月27日收到修改稿)

设计了一种双开口Helmholtz周期结构,该周期结构单元采用双开口内外腔设计,基于多腔耦合局域共振机理,可大大增加局域共振区域,增加能得到较低的低频带隙特性.通过设计调节内腔弧长,可以使带隙移动,达到特定低频频段的隔声效果.在分析低频带隙形成机理和影响因素时,采用声电类比原理建立带隙起始频率和截止频率的计算数学模型并与有限元方法进行对比分析.研究表明:该结构具有良好的低频带隙特性,其最低带隙段为86.9—138.2 Hz.外径一定的条件下,低频带隙受内腔弧长、内外腔间隔以及周期单元结构间隔影响,内腔弧长越长,低频带隙越低;内外腔间距离越大,从而内腔体积变小,带隙向高频移动,其低频效果变差;减小结构间距对低频带隙起始频率无影响,但可以大大增加低频带隙截止频率,从而增加带隙宽度.该研究结论可以为低频降噪领域提供一定的实践和理论支持.

Helm holtz共振,周期结构,低频带隙,声电类比

1 引 言

近年来,以声子晶体和声学超材料为代表的人工周期结构受到了越来越多研究者的关注.在人工周期结构中,周期变化的结构参数使之具有“带隙”特性.其带隙特性表现为:频率在带隙范围内的声波或弹性波在结构中不会传播,这种特性为该种结构或材料在隔振降噪领域的应用打下了基础.长期的研究表明,人工周期结构带隙的产生主要有两种机制:一种是Bragg散射机制[1−3],另一种是局域共振机制[4,5].Bragg散射型声子晶体中的带隙称为Bragg带隙,其产生受Bragg条件控制——晶格尺寸至少要与弹性波的半个波长大致相当.因此,为了得到低频Bragg带隙,需要的声子晶体尺寸往往很大,而不便于实际应用.局域共振机制由Liu等[4]首次提出,他们发现这种新型声子晶体可以在小尺寸条件下产生非常低频的带隙(晶格尺寸远小于带隙频率对应的弹性波波长),大大突破了传统Bragg散射型声子晶体的局限,从而达到了“小尺寸控制大波长”的目的.局域共振型声子晶体同时可以表现出负等效质量密度、负等效模量等新奇特性[6−12].

当前,采用人工周期结构处理隔振降噪问题的主要发展方向为设计“轻质小巧、低频宽带”的结构.Helmholtz共鸣腔利用了空气的共振特性,只需进行结构设计而无需另外附加质量便使其在轻质和低频设计上具有良好的优势,得到了众多学者的认可.Fang等[13]利用Helmholtz共振原理设计的周期结构首次实现了结构在特定的频率段具有负的杨氏模量.Ding等[14,15]提出了一种可控二维Helmholtz周期结构,理论分析和实验表明其也存在负杨氏模量.Guan等[16]设计了回旋结构的Helmholtz共鸣器,得到了很好的低频带隙.Li等[17]设计了多层开口环结构,打开了较低的低频带隙,并利用声电类比方法对影响其带隙的参数进行了分析.刘敏等[18]通过对二维正方排列圆柱Helmholtz共振腔阵列声特性的研究,指出局域共振型声子晶体中存在共振单元与基体的弱耦合作用及共振单元间的耦合作用.Murray等[19]基于Helmholtz共鸣原理设计了双层渔网结构(double fishnet),获得了在中高频段良好的隔声效果.

当前的Helm holtz共鸣器周期结构研究中,考虑低频特性较少,尤其是100 Hz以下的低频段.主要原因是Helmholtz共鸣器周期结构设计中,受开口数量和深度的影响,其局域共振区域较小,导致低频特性的获取往往需要较大的体积.本文中,周期结构单元采用双开口内外腔设计.双开口设计增加了共鸣器与外部空气联通的区域;特有的内外腔设计,增加开口深度,以求增大协同共振区域,使共振频率下降;在共振频率附近,由于空气被局域在结构内部,声波不能传播,达到隔声的目的,在能带特性上表现为能带下移,因此可以得到较低的低频能带特性.同时通过内腔弧长的调整,可以使带隙频段移动,达到低频带隙频段可调的目的.在分析其低频带隙形成机理的过程中,建立了低频带隙电路等效计算数学模型,并与有限元法对比分析.该数学模型使结构设计难度大大降低,节约大量的有限元计算时间,同时通过数学模型的建立,可以完成结构参数对带隙影响的定量分析,能深入揭示该结构的结构参数对低频带隙的影响.

2 双开口局域共振声子晶体低频带隙

双开口局域共振单元结构横截面如图1(a)所示,该结构为内外两腔的圆柱结构,制作材料为钢.外腔半径为r;开口宽度分别w1,w2;管壁厚度为d;内腔弧角度β;两腔间隔为w0.在结构设计中,通过调整内腔弧角度β,可以改变结构,达到带隙可调的目的.

为了探究该结构的能带结构和共振模态,取结构参数为a=100 mm,r=45 mm,w0=1 mm, d=1mm,w1=2mm,w2=2mm,β=180◦的模型作为研究对象.对空气域来说,声压Helmholtz方程的频域表达式为

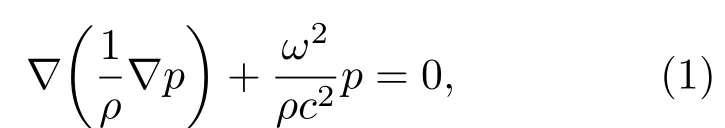
式中,p为声压,ω为角频率,c为声速,ρ为空气密度.

空气的声阻抗较固体钢小得多,由于这两种介质声阻抗差异大、不匹配,声波很难从一种介质传播到另一种介质.空气中传播的声波几乎都在固体间反射,很难透射过去,可以认为声波透过固体钢的能量很小,能够引起固体振动的能量非常小,几乎可以忽略,因此在计算中将腔壳视为刚体,不考虑其振动.根据Bloch理论,该结构中采用Bloch-Floquet边界,其表达式为

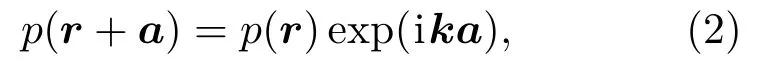
图1 (a)双开口Helm holtz单元横截面;(b)双开口Helm holtz结构5元胞有限结构Fig.1.(a)The unit structure’s cross section of the double-sp lit Helm holtz resonant structure;(b)the finite structure w ith 5 cells of the doub le-sp lit Helm holtz resonant structure.

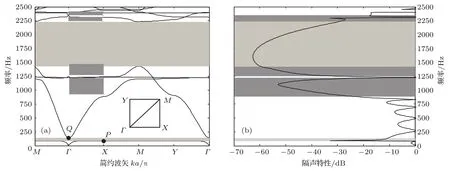
图2 (a)双开口Helm holtz单元能带结构图;(b)双开口Helm holtz单元隔声曲线Fig.2.(a)Band d iagram of the doub le-sp lit Helm holtz resonant structu re;(b)the transm ission spectra of the doub le-sp lit Helm holtz resonant structu re.

式中,r是位置矢量;a为声子晶体晶格常数;参数k为波矢,它描述了相位和定义边界条件与元胞的关系.在给定的波矢条件下,通过解谱方程可以得到一组特征值和特征向量,而在第一Brillouin区边界上的波矢所对应的特征向量代表了特征模态的声压.

为了计算所提出结构的声波传输特性,定义了由5个有限个元胞组成的周期结构.其结构在y方向上是无限周期,在x方向为5个元胞组成,如图1(b)所示,在结构上下边应用周期边界条件,而在两端应用完美匹配层.

对于有限声子晶体结构,隔声量(或称传声损失)可以由下式计算得出:

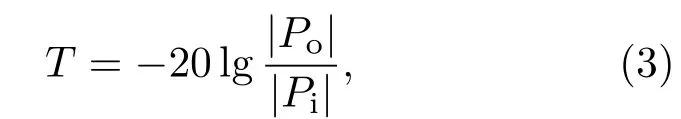
式中Po为输出声压,Pi为入射声压.通过改变平面波传输频率,重复计算后得到隔声曲线.经过计算得到的带隙结构和隔声量如图2(b)所示.

采用COMSOL Multiphysics仿真软件(声学模块),使用软件模块中默认三角网格划分,对带隙结构和传输频谱进行计算,结果如图2所示.可以看出,在2500 Hz以下的频段,该结构具有两条完整振带隙,如图2(a)中浅灰色部分.其中,在第一能带和第二能带之间为最低的带隙,其带隙宽度为87.1—138.2 Hz.第2条完整带隙分别为1428.5—2231.7 Hz.同时注意到,该结构在Γ-X方向也具有四条方向带隙,如图2(a)中深灰色部分.为了验证带隙结构计算的正确性,同时给出了5元胞有限结构的隔声特性图作为对比,如图2(b)所示.前面提到,在带隙内波的传播将会受到抑制,由隔声特性图可以看出,在全带隙以及Γ-X方向带隙频段声波受到了极大的抑制,且抑制范围与带隙宽度符合度较好,说明了带隙计算的正确性.

进一步分析,第一能带在大部分Brillouin区呈现出了较长的平直状态,说明该结构存在着局域共振模态,其第一带隙为局域共振带隙.对于第二完全带隙,其为Bragg带隙,其出现的频率位置主要受Bragg条件控制,Bragg条件表明,要在声子晶体中实现Bragg带隙,其晶格尺寸至少要与弹性波的半个波长大致相当.其带隙频率中心可由下式得到:

其中,c代表声子晶体中基体弹性波波速,a代表晶格常数.因此,在Bragg散射型声子晶体中,其第一带隙中心频率一般位于c/(2a)附近.则该结构第一Bragg带隙中心频率根据晶格常数及空气中声速计算,即f0=c0/(2a)=1715 Hz,与能带结构图2(a)相符合.同时由(4)式也可以看出,第二带隙形成主要受晶格常数影响,与结构设计并无太大关系,元胞结构主要影响低频带隙,因此在下文中,主要分析结构对低频带隙形成机理的影响因素.

3 低频带隙形成机理及等效建模分析

从图2带隙图可以看出,第一能带在大部分Brillouin区呈现出了较长的平直状态,这说明该结构存在着局域共振模态.为了进一步研究结构低频带隙形成机理,选取了低频全带隙中的上下限点(如图2(a)所示P,Q点)的声压场,对低频带隙形成机理进行分析.

图3(a)表示P模态的声压场,可以看出,声压几乎全部局限在圆腔内部,而在外部声压场压力很小,几近于0.而在内外腔形成的环形通道内,声压场是变化的,在外部几乎近于0,而越靠近圆形内腔,其声压强度越大.因此可以认为P模态主要是声波在该结构形成了共振,声波能量局限于结构当中,在外部不能传播.模态P事实上也决定了低频带隙的下限.而Q模态则与P模态完全相反,由图3(b)可以看出声压全部集中于结构外部,而结构内部声压几乎为0,环形通道内,声压的变化也与P模态相反,外部高,内部低.这说明声波在结构外部传播,结构对声波传播没有作用.因此Q模态决定了带隙的截止点,是低频带隙的上限.可以采用声电类比方法建立数学模型,进一步分析两种模态对带隙的影响.

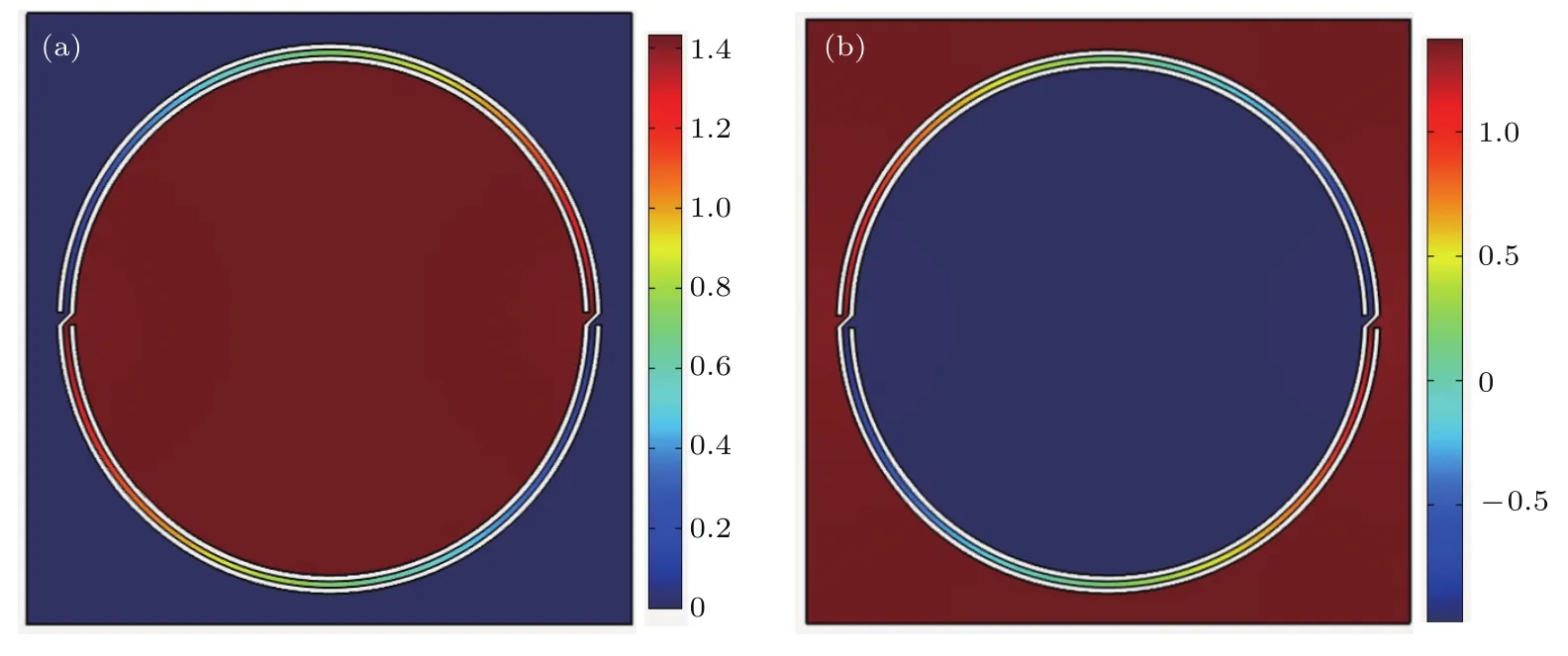
图3 (网刊彩色)(a)模态P声场压力图;(b)模态Q声场压力图Fig.3.(color on line)(a)The sound p ressu re d istribu tion diagram s of point P;(b)the sound p ressure distribution diagram s of point Q.

为了便于叙述,在分析双开口Helmholtz共振周期结构带隙形成的机理过程中,将结构其划分为四部分,其划分区域如图4所示,其中A代表结构外空气层;B,C为内外腔形成的环形通道;D为圆形内腔.

图4 结构区域划分示意图Fig.4.The region d ivision of the cross section in structu re.

对于模态P,由于结构外部的声压场几乎为0,模态P中主要是由B,C,D三个区域协同共振产生,与区域A无关,因此不考虑A区域.根据声电类比原理,狭长的环形通道B,C可以等效为电感LB,LC,而圆形内腔等效为电容CD,其构成的电路如图5所示.

图5 模态P等效电路图Fig.5.The equivalent circuit of point P.

图5中LB,LC为等效电感,其表达式为

模态P的共振频率计算公式为

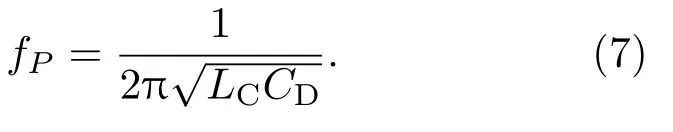
对于模态Q,由于A,B,C和D四个区域都具有声压场,因此在对模态Q进行声电类比中,要完全考虑四个区域,其中,A区域等效为电容,则其构成的谐振电路如图6所示.

图6 模态Q等效电路图Fig.6.The equivalent circuit of point Q.

4 低频带隙影响因素分析

上文建立了双开口Helm holtz的低频带隙上下限的数学模型,该模型将有利于我们对影响低频带隙的因素进行分析.根据(5)—(9)式,影响该结构低频带隙的因素主要有:内腔弧角β,环之间的间隔w0,晶格常数a也即结构周期排列间隔a−2r.其中,内腔弧角β是主要因素,内腔弧角的改变将会使结构发生较大的改变,导致内外腔形成的环形通道长度以及内腔的体积改变,从而改变了协同共振区域,影响Helmholtz共鸣器的等效参数.下面我们分别对这三个影响因素进行分析.

为了控制变量便于比对分析,在分析双开口Helmholtz共鸣器的内腔弧角β对低频带隙的影响时,设定环之间的间隔w0=1 mm,晶格常数a=100 mm.当内腔弧角β从15◦增加到180◦时,分别采用建立的带隙声电类比数学模型和有限元软件进行带隙上下限计算,并进行对比验证,得到内腔弧角β对低频带隙的影响,结果如图7所示.

图7中红色、蓝色以及绿色虚线分别代表采用声电类比数学模型计算的第一低频带隙的上限、下限和带隙宽度.而倒三角、三角以及圆形代表采用有限元计算方法计算的第一低频带隙的上限、下限和带隙宽度(以下图例均如此,不再赘述).由图7可以看出,采用声电类比计算结果与采用有限元计算的结果误差较小,说明建立模型的正确性.随着β的增加,第一低频带隙的上限和下限不断降低.内腔弧角β的增加实际上使环间通道长度增加,使等效电感大大增加,同时也减小了最后形成空腔的面积,但减小的面积相对较小,从而使等效电容变化较小.第一带隙下限只与B,C和D区域有关,B, C区域等效电感的增加和D区域等效电容小幅度减小,最终使第一带隙下限不断下降,得到较好的低频特性.对于第一带隙,其上限是由四个区域协同共振的结果,等效电容为CACD/(CA+CD).可见,随着等效电感的增加,其等效电容进一步减小,但由于区域A电容保持不变,同时区域A等效电容小于内部空腔电容,其电容等效结果减小不大,小于因内腔弧角β变大而使环形通道长度增加导致的等效电感增加幅度,因此上限带隙也降低.通过设计调节内腔弧角β,可以使带隙移动,达到特定频段隔声的效果.

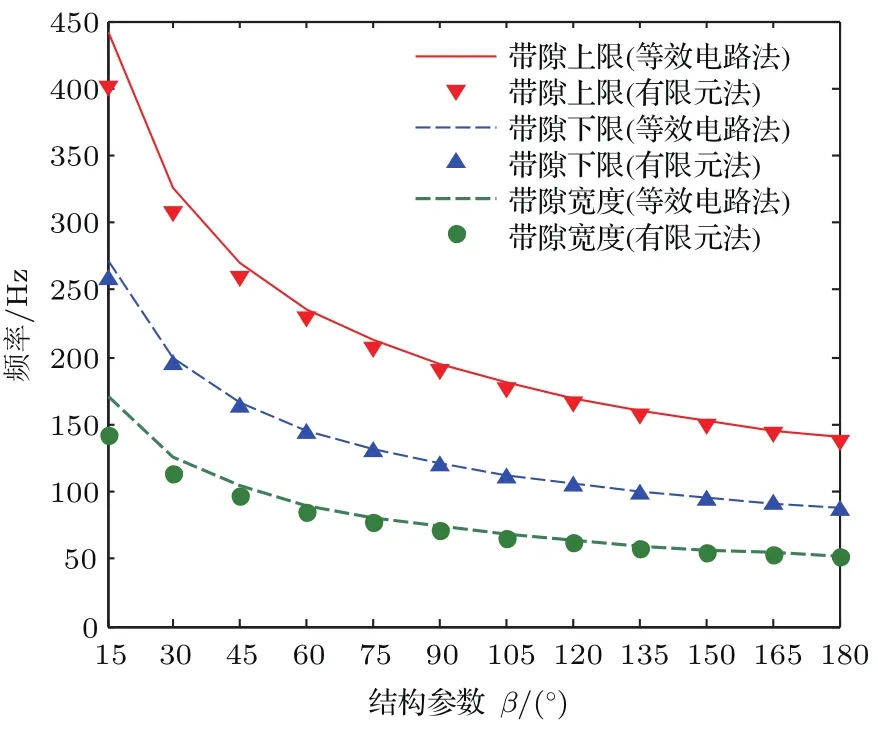
图7 (网刊彩色)内腔弧角β对第一低频带隙的影响Fig.7.(color on line)The im pact of the param eterβ on fi rst low frequency band-gap.

分析双开口Helmholtz共鸣器的环间间隔w0对低频带隙的影响时,设定晶格常数a=100mm,内腔弧角β=180◦.当环间间隔w0从1 mm增加到4 mm时,分别采用建立的带隙声电类比数学模型和有限元软件进行带隙上下限计算,并进行对比验证,得到环间间隔w0对低频带隙的影响如图8所示.

从图8可以看出,在前半段声电类比计算值与有限元计算值误差较小,但是w0从2 mm增加到4 mm时,其误差明显增大.分析其原因主要是由于环间间隔增大,在环间构成的环形通道已不再是细管道,失去了Helm holtz声电类比的前提条件,导致计算误差增加,但整体趋势与实际值保持了一致.不难看出,随着环间间隔的不断增加,在等效电感变化不大的情况下,其内腔的面积大大减小,从而使等效电容大大减低,导致第一低频带隙的上下限均呈现增大趋势.带隙明显向高频移动,带隙宽度有所增加但其低频特性已大大降低.

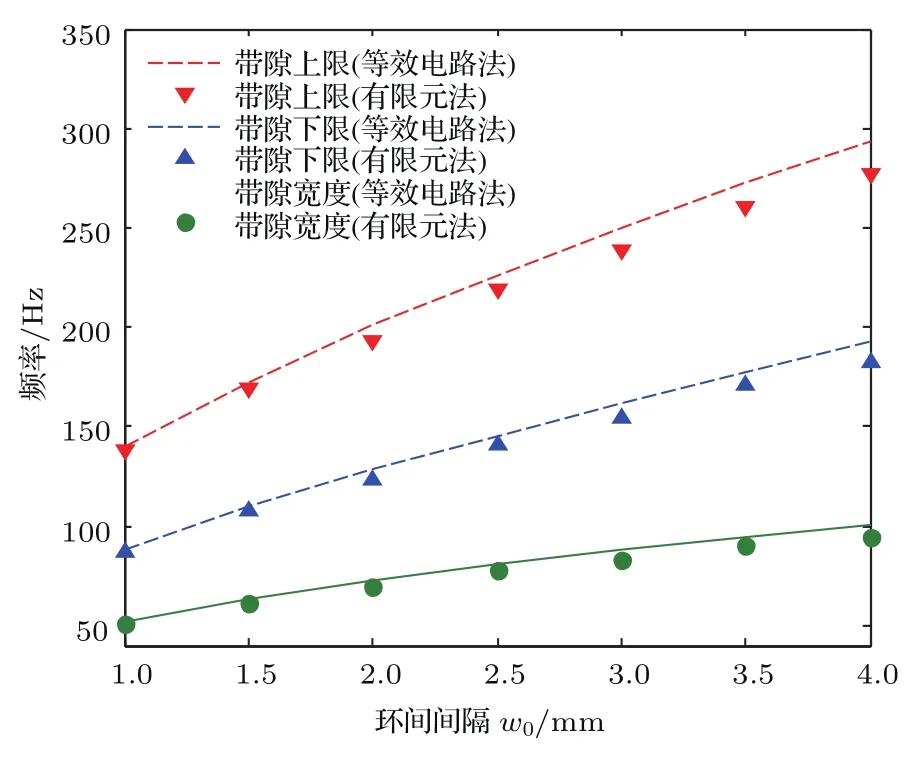
图8 (网刊彩色)环间间隔w0对第一低频带隙的影响Fig.8.(color on line)The im pact of the param eter w0on fi rst low frequency band-gap.

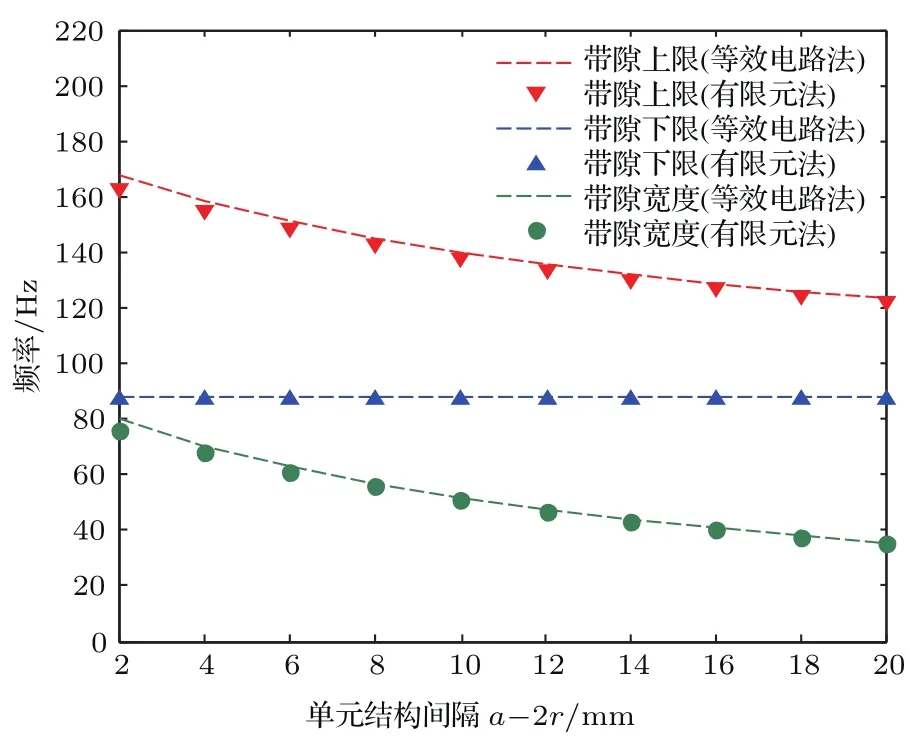
图9 (网刊彩色)结构周期排列间隔对第一低频带隙的影响Fig.9.(color on line)The im pact of interval between each rings on low frequency band-gap.

分析双开口Helmholtz共鸣器的结构周期排列间隔a−2r对低频带隙的影响时,设定环间间隔w0=1mm,内腔弧角β=180◦.当结构周期排列间隔a−2r从2mm增加到20mm时,分别采用建立的带隙声电类比数学模型和有限元软件进行带隙上下限计算,并进行对比验证,得到结构周期排列间隔a−2r对低频带隙的影响如图9所示.

图9表示周期排列间隔对带隙结构的影响,可以看出,周期排列间隔对带隙下限基本没有影响,但对带隙上限具有较大的影响.具体表现为:随着排列间隔增加,其带隙上限不断下降,带隙宽度也随之减小.从等效电路模型可知,排列间隔减小,即晶格常数a的减小,其A区域等效电容减小,则与空腔内等效电容串联后的电容变小,导致频率上升,当排列间隔2 mm时,其带隙上下限分别为87.2 Hz和162.7 Hz,其带隙范围大大增加.从另一方面来说,减小了结构间的缝隙,即增大了填充率,其带隙宽度能较大地扩宽.

5 结 论

在解决低频降噪问题时,由于质量密度定理,常规方法导致结构质量和体积较大,“低频、轻质、宽带”成为追求的方向.本文建立了一种双开口Helmholtz周期结构,无需附加质量,对于解决轻质问题奠定了基础.双开口Helmholtz周期结构特有的内外腔设计,增加开口深度,使共振区域增加,得到较低的低频能带特性.调整内腔弧长,可以使带隙频段移动,达到低频带隙频段可调的目的.通过增加内腔弧长、减小内外腔间隔和减小结构单元间隔可以大大扩宽低频带隙宽度,达到低频宽带的目的.这些结论的获得将有益于该结构在隔声降噪尤其是低频降噪领域的应用.

[1]Lai Y,Zhang X,Zhang Z Q 2001 Appl.Phys.Lett.79 3224

（5）部分招标，半招半定。招标时将工程项目分解，只招其中一部分，其他部分按设计变更或追加项目送给关系户来施工；

[2]Hussein M I,Hu lbert G M,Scott R A 2006 J.Sound Vib.289 779

[3]Hussein M I,Hu lbert G M,Scott R A 2007 J.Sound Vib.307 865

[4]Chen Y,Li J,Zhou J,Huang T,Zhou M,Yu D Y 2014 Shock Vib.2014 189539

[5]Liu Z Y,Zhang X X,M ao Y W 2000 Science 289 1734

[6]Liu Z,Chan C T,Sheng P 2005 Phys.Rev.B 71 014103

[7]Li J,Chan C T 2004 Phys.Rev.E 70 055602

[8]Deng K,D ing Y,He Z,Zhao H,Shi J,Liu Z 2009 J. Appl.Phys.105 124909

[10]Zhang S,Y in L,Fang N 2009 Phys.Rev.Lett.102 194301

[11]M ei J,M a G,Yang M,Yang Z,W en W,Sheng P 2012 Nat.Comm un.32 756

[12]Zhou X,Bad redd ine Assouar M,Oud ich M 2014 J.Appl. Phys.116 194501

[13]Fang N,X i D,Xu J,Am bati M,Srituravanich W,Sun C 2006 Nat.M ater.5 452

[14]D ing C,Hao L,Zhao X 2010 J.Appl.Phys.108 074911

[15]Hao L M,D ing C L,Zhao X P 2012 Appl.Phys.A 106 807

[16]Guan D,W u J H,Li J,Gao N S,Hu M 2015 Noise Control Eng.J.63 20

[17]Li J,W u J H,Guan D,Gao N S 2014 J.Appl.Phys. 116 103514

[18]Liu M,Hu Z L,Fu X J 2012 Acta Phys.Sin.61 104302 (in Chinese)[刘敏,候志林,傅秀军 2012物理学报 61 104302]

[19]M urray A R J,Summ ers I R,Sam b les J R,H ibbins A P 2014 J.Acoust.Soc.Am.136 980

PACS:43.20.+g,42.50.Gy,46.40.FfDOI:10.7498/aps.66.064301

Low frequency band gap characteristics of doub le-sp lit H elm holtz locally resonant period ic structu res∗

Jiang Jiu-Long1)Yao Hong2)†Du Jun1)Zhao Jing-Bo2)Deng Tao3)

1)(Aeronautics and Astronau tics Engineering College,A ir Force Engineering University,X i’an 710038,China)

2)(Science of College,A ir Force Engineering University,X i’an 710051,China)
3)(X i’an Flight College of A ir Force,X i’an 710306,China)
(Received 12 August 2016;revised m anuscrip t received 27 Decem ber 2016)

A doub le-sp lit Helm holtz periodic structurew ith the characteristic of local resonance is designed and constructed in this paper.The doub le-sp lit periodic structural cellwhich can be divided into internal and external cavities is adop ted in structure.In such a kind of structure,the resonating area is rem arkably expanded while the inner cavity is continuously enlarged.Thus,a satisfactory feature of low frequency resonance can be obtained.A t the sam e tim e,the ad justability of band gap is achieved by the designed ad justment of the arc length of the inner cavity,therefore,the eff ect of sound insulation in a specific low frequency band can be achieved.In the analysesof them echanism and factorsof the generation of low frequency band gap,them athem aticalm odel of the upper and lower lim its of the band gap is established by using the electric circuit analogy.And some com parative analyses between themethods of electric circuit analogy and finite elem ent m ethod are carried out.The result suggests that a satisfactory feature of low frequency band gap is presented, and the fi rst band-gap ranges from 86.9 Hz to 138.2 Hz.The low frequency band gap can be influenced by the arc length of inner cavity,the space between inner and outer cavities,and the interaction of the structural cells in the periodic arrangem ent.The longer the arc length of the inner cavity,the lower the low frequency band gap w ill be;the longer the distance between inner and outer cavities,and the higher the frequency of band gap,the worse the low frequency eff ect w ill be;the lower lim it of low frequency band gap cannot be in fluenced by reducing the space between individual structures,on the contrary,the w idth of low frequency band gap can be sharp ly increased.Plenty of practical and theoretical support in the field of low frequency noise reduction is off ered in the research.

Helm holtz resonance,periodic structure,low frequency band gap,electric circuit analogy

10.7498/aps.66.064301

∗国家自然科学基金(批准号:11504429)资助的课题.

†通信作者.E-m ail:yyyyaaohhong@sohu.com

*Pro ject supported by the National Natural Science Foundation of China(G rant No.11504429).

†Corresponding author.E-m ail:yyyyaaohhong@sohu.com