线性吸收介质非局域线性电光效应的耦合波理论∗
吴丹丹1)2) 佘卫龙1)
1)(中山大学,光电子材料与技术国家重点实验室,广州 510275)
2)(华南理工大学物理教学实验中心,广州 510006)
(2016年9月30日收到;2016年11月15日收到修改稿)
线性吸收介质非局域线性电光效应的耦合波理论∗
吴丹丹1)2) 佘卫龙1)†
1)(中山大学,光电子材料与技术国家重点实验室,广州 510275)
2)(华南理工大学物理教学实验中心,广州 510006)
(2016年9月30日收到;2016年11月15日收到修改稿)
本文提出了线性吸收介质非局域线性电光效应的耦合波理论,建立了相应的耦合波方程组,并求解了该方程组.由此,可给出在任意方向外加电场的作用下,光在具有空间非局域响应的线性吸收介质中沿任意方向传播时出射光场的表达式.据此,研究了线性吸收是如何改变出射光场的两个偏振分量的振幅、相位和波形的.进一步讨论了线性吸收对电光强度调制的影响,以及如何测量一阶线性和二阶非线性极化率非局域响应的特征长度和介质的线性吸收系数.
线性电光效应,非局域,线性吸收,电光调制
1 引 言
线性电光效应是一种重要的光学现象,在电光调制和电光开关等方面有着非常广泛的应用[1−8].折射率椭球理论[9]以其直观和简洁,长期以来被广泛应用于线性电光效应的各种理论分析中.但此理论存在着局限:首先,晶体加电场后其折射率椭球方程的主轴化往往是一件很困难的事,况且还要计算沿光传播方向上的折射率;其次,折射率椭球理论不能用来处理存在线性吸收或极化率张量具有非局域响应等情况下的线性电光效应.为了绕开这些限制,科研工作者们先后提出了一些新的处理线性电光效应的理论[10−12].在2001年,She和Lee[13]提出了线性电光效应的耦合波理论,该理论可以用来描述在任意方向的外加电场的作用下,光在任意对称点群的晶体中沿任意方向传播时的线性电光效应.此耦合波理论从根本上克服了折射率椭球理论的种种局限,为线性电光效应的理论和应用的研究开辟了新方法.现在线性电光效应的耦合波理论已经被成功应用于处理具有线性吸收的介质中的线性电光效应[14,15],也相继提出了线性电光效应与其他光学效应级联的耦合波理论[16−19]. 2016年初,在不考虑介质存在吸收的情况下,我们建立了非局域线性电光效应的耦合波理论[20].
本文从麦克斯韦方程组出发,在考虑介质具有线性吸收的情况下发展了非局域线性电光效应的耦合波理论,建立了相应的耦合波方程组,并求解了该方程组.研究表明:首先,当线性吸收介质中两个吸收系数α11和α22相等时,线性吸收仅使介质中光场的振幅衰减,而不影响其相位和波形,因此,与无吸收介质中的情况一样,可以认为电光强度调制时出射光束不再保持高斯光束波形的现象是二阶非线性极化率存在非局域响应的一个可能信号;其次,当α11与α22不相等时,线性吸收使介质中光场的振幅衰减,相位改变,此时,线性吸收会导致电光强度调制时出射光束的波形不再保持高斯光束波形,因此不能简单地根据出射光波形是否偏离高斯型来判断是否存在非局域响应,但可通过测量非局域响应的特征长度值σ2来判断是否存在非局域响应;在α11̸=α22的情况下,线性吸收还使电光强度调制的消光比减小,但对半波电压没有明显影响.最后,我们讨论了测量一阶线性和二阶非线性极化率非局域响应特征长度σ1和σ2以及晶体吸收系数α11和α22的方法.
2 基本理论
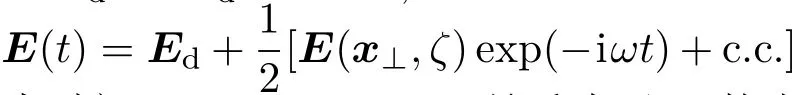
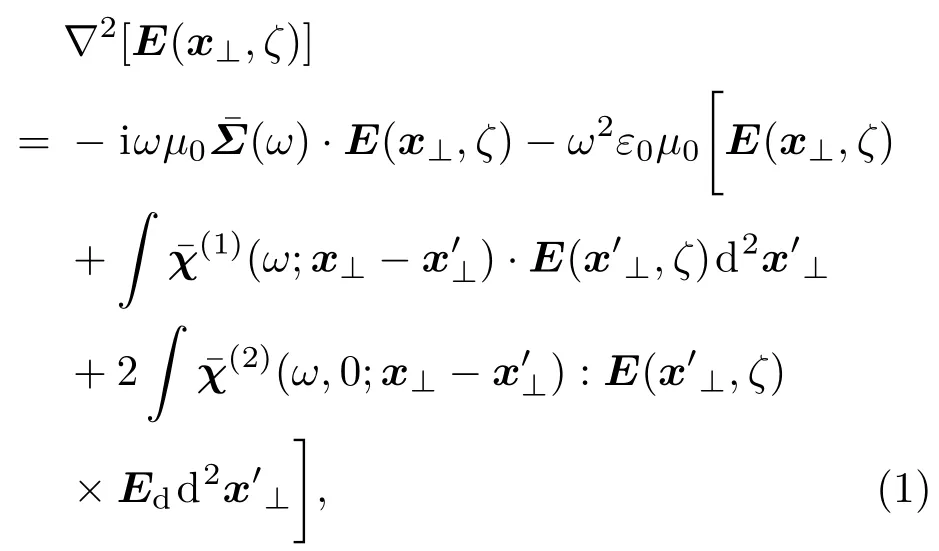
其中,µ0为真空中的磁导率;ε0为真空中的介电常数;为晶体的电导率张量;是横向的面积元,积分的上下限分别为∞和−∞;和分别是一阶线性和二阶非线性的非局域极化率张量(后文中,在不引起歧义的情况下会将其分别简写为和,并且都是实数(实际应用中,如果有虚部存在,则应将其虚部并入方程右边第一项内).此处,我们认为由于相位失配,只需考虑线性电光效应的贡献,而忽略了其他二阶及更高阶的非线性光学效应[19].
这里,我们考虑最简单的情况[20],即
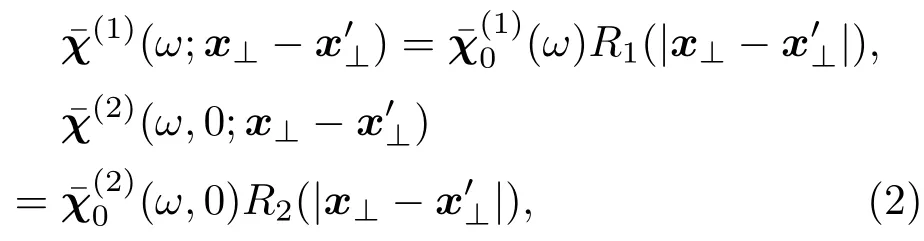
对于傍轴光束E(x⊥,ζ),我们可以仅考虑其横向分量(垂直于eζ的分量),而忽略其纵向分量(平行于eζ的分量).这样E(x⊥,ζ)可以表示为
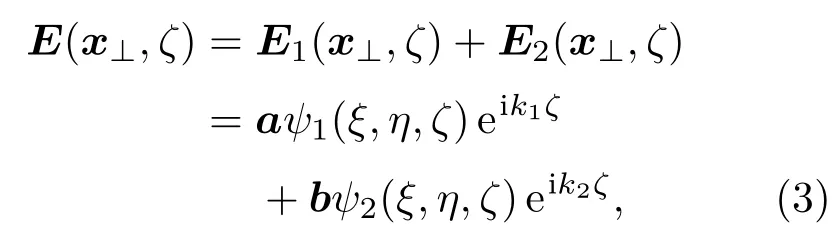
这里,k1和k2分别为光场E1(x⊥,ζ)和E2(x⊥,ζ)的波数.当k1=k2时,E1(x⊥,ζ)和E2(x⊥,ζ)分别代表光场两个相互垂直的分量;当k1̸=k2时, E1(x⊥,ζ)和E2(x⊥,ζ)分别代表两个经历不同折射率的相互垂直的独立分量,a和b分别为代表E1(x⊥,ζ)和E2(x⊥,ζ)方向的两个单位矢量,并且a·b=0,而ψ1(ξ,η,ζ)和ψ2(ξ,η,ζ)是两个慢变振幅包络.将(2)和(3)式代入方程(1)中,把与相关的项当成微扰[13],整理后得到以下的耦合波方程组:
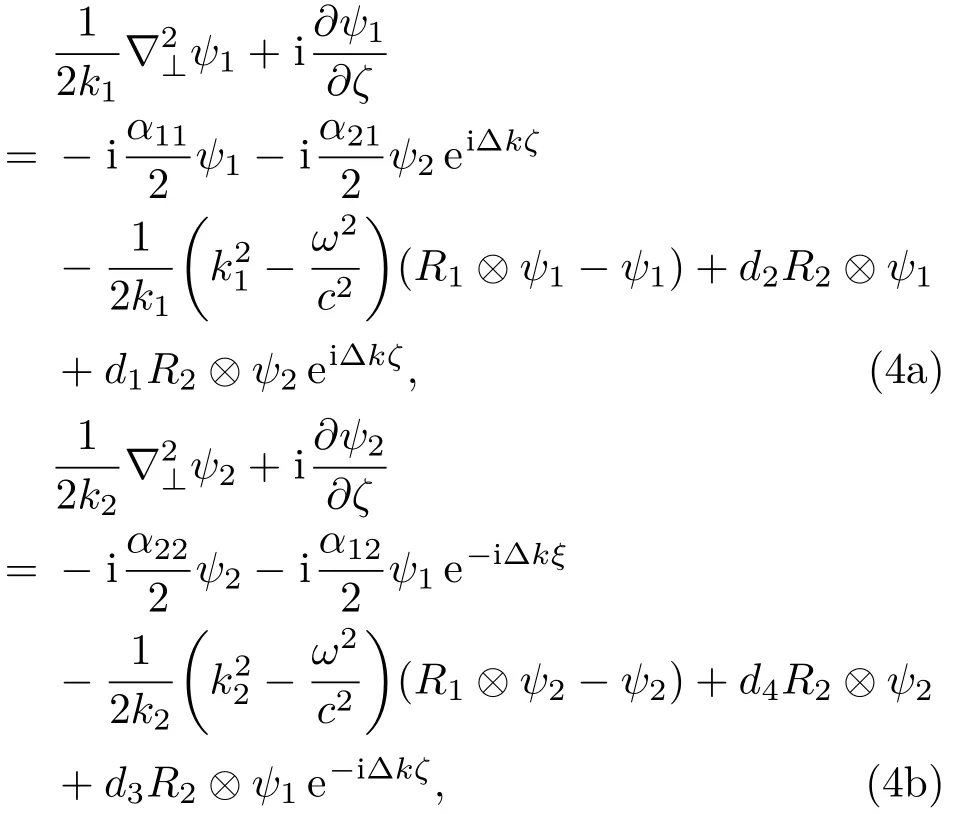
其中,

α11,α12,α22和α21是晶体的吸收系数[15].在方程组(4)中,为了使表达式结构简洁,将ψj(ξ,η,ζ)写成ψj,将Rl(|x⊥−x′⊥|)写成Rl(后文中做类似处理时不再另行说明),用表示Rl和ψj的卷积,即
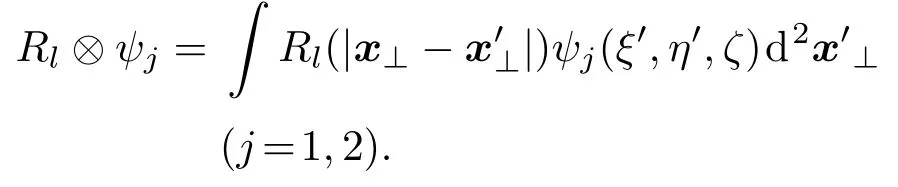
方程组(4)可以用来描述在任意方向外加电场的作用下,光在线性吸收晶体中沿任意方向传播时的非局域线性电光效应,其中响应函数的具体形式要根据引起非局域的物理机制来定[23].精确求解方程组(4)会存在困难,但在给定各参数的情况下,可以进行数值求解.
下面,我们仅考虑弱非局域[23]的情况,此时Rl(|x⊥|)的特征长度远小于ψj(ξ,η,ζ)的束宽.因此有
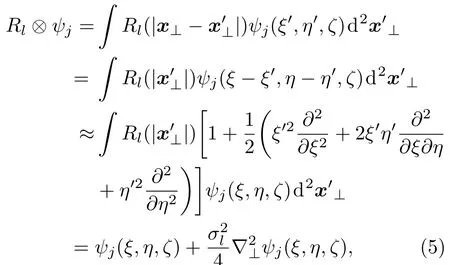
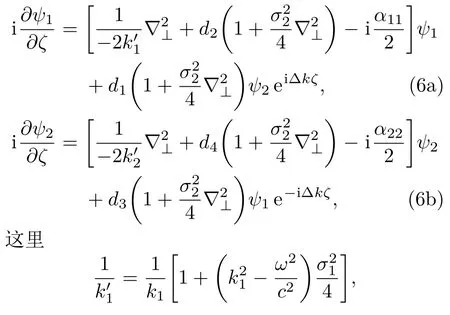
容易看出,当光束E1(x⊥,ζ)和E2(x⊥,ζ)的束宽为无穷大时,就会有,方程组(6)就简化成文献[14]中描述的线性吸收介质中局域情况下的线性电光效应.
如果外加电场Ed=0,则d1=d2=d3= d4=0,那么方程组(6)变成
对应的出射光强为
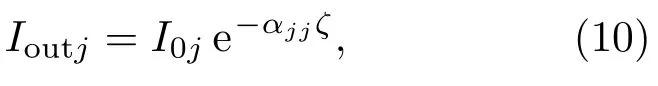
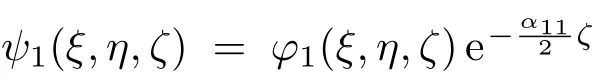
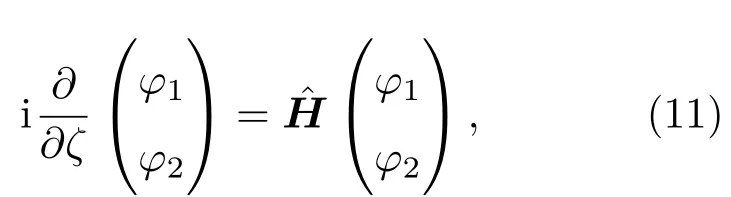
其中
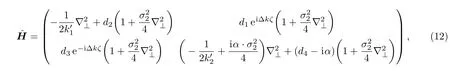
这里,α=(α22−α11)/2,它反映了吸收系数α11与α22的不同.容易验证下面的恒等式

其中
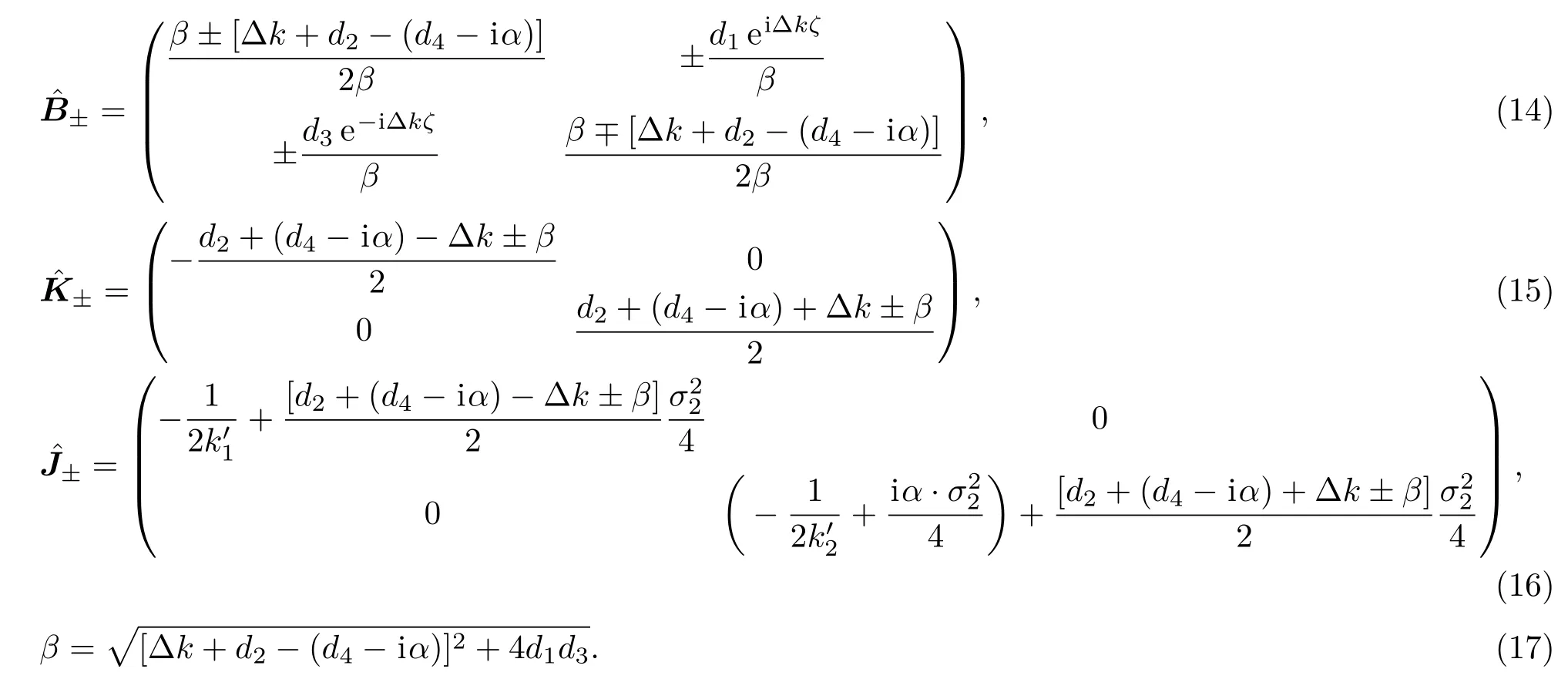
当Δk=0,α=0,即k1=k2和α11=α22时,我们发现是一个常数矩阵,因此.另一方面,对大多数的双折射晶体,当k1和k2不是太靠近光轴[13]时,条件|Δk|≫|dm|成立(m=1,2,3,4),这使得近似为一个对角矩阵,从而得到.对这两种情况,(13)式变成

做变换
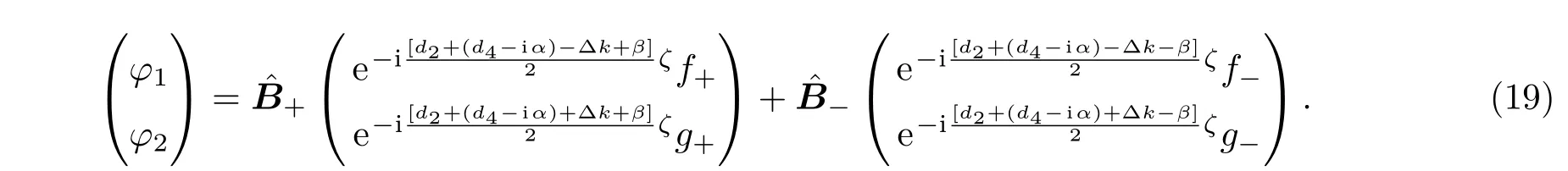
把(18)和(19)式代入方程(11)中,整理后可得

如果
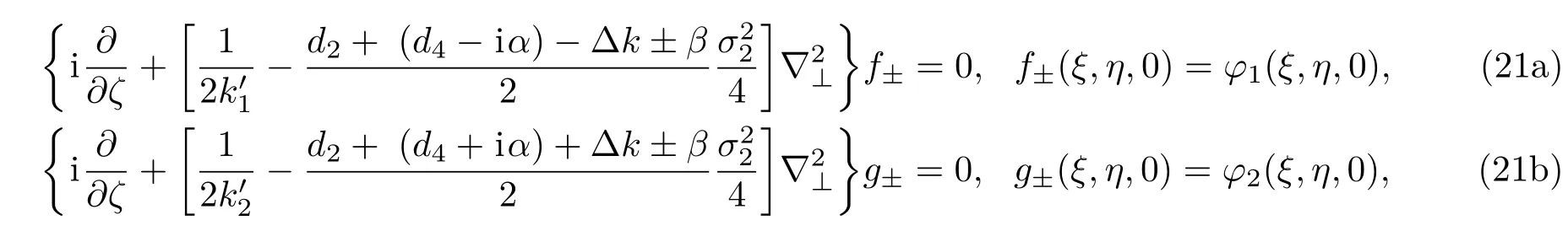
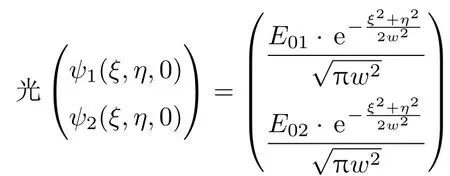

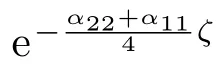
对于局域情况σ1=σ2=0,方程组(6),(22)和(23)式就变成描述线性吸收介质中入射光是高斯光束时的线性电光效应的耦合波方程组及其解析解.这正好弥补了之前的线性吸收介质线性电光效应的耦合波理论只讨论入射光是平面波的情况的不足[14].
3 分 析
3.1 k1=k2且α11=α22
当光沿着单轴晶体的光轴方向传播,或者在¯43m和23对称点群的晶体中传播时,我们有eξ=ex,eη=ey和eζ=ez((x,y,z)为晶体的介电主轴坐标系,ex,ey,ez分别为三个坐标轴的方向矢,对单轴晶体ez代表单轴晶体的光轴方向),以及k1=k2,Δk=0和d1=d3,同时α11=α22(即α=0).对振幅调制,我们把两个正交的偏振片P1和P2分别放在晶体的入射面和出射面处.此时, a=ex平行于P1,b=ey平行于P2.对于入射条件E01=E0,E02=0,由(22)式,我们可以得到从偏振片P2出来的光场为
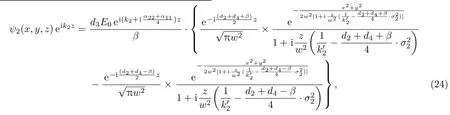
出射光的强度为
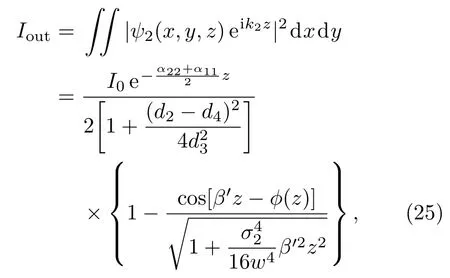
其中,I0=|E0|2是入射光的光强,
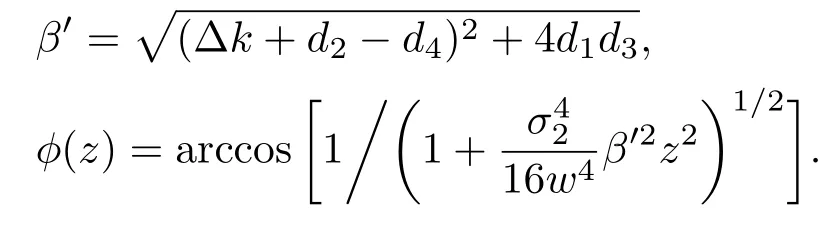
由(24)和(25)式可知,电光强度调制时,线性吸收只是使出射光场的强度衰减,而对出射光场的波形,电光调制的半波电压和消光比都没有影响.所以与无吸收介质中的情况一样,出射光场不再保持高斯光束波形这一现象可以被认为是¯χ(2)存在非局域效应的一个可能信号.由(25)式可知,给定各参数,调节Ed,当β′z−ϕ(z)=π时,电光强度调制的出射光强Iout达到最大值,此时有
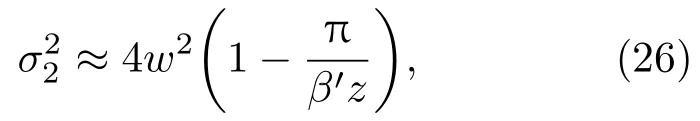
这样就获得了σ2的值.
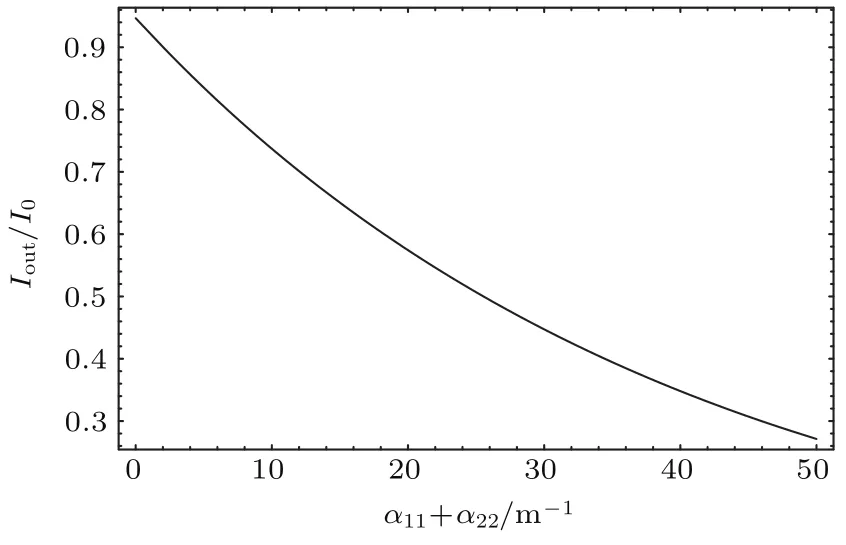
图1 Iout/I0随α11+α22的变化,其中,d2=d4= 0 m−1,d1=d3=71.2494 m−1Fig.1.The dependence of the ou tpu t intensity Iout/I0on the absorp tion coeffi cientα11+α22.Here d2= d4=0 m−1,d1=d3=71.2494 m−1.
3.2 |Δk|≫|dm|
此处,不失一般性,我们设置k1>k2,这样β≈ −Δk−d2+d4−iα.对于振幅调制,设θ是偏振片P1和a之间的夹角,且E01=E0cosθ, E02=E0sinθ为入射光束的振幅.由(22)式,我们可以得到从偏振片P2出来的光场为
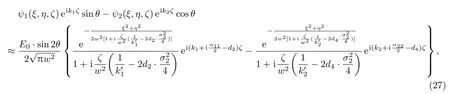
出射光的光强为
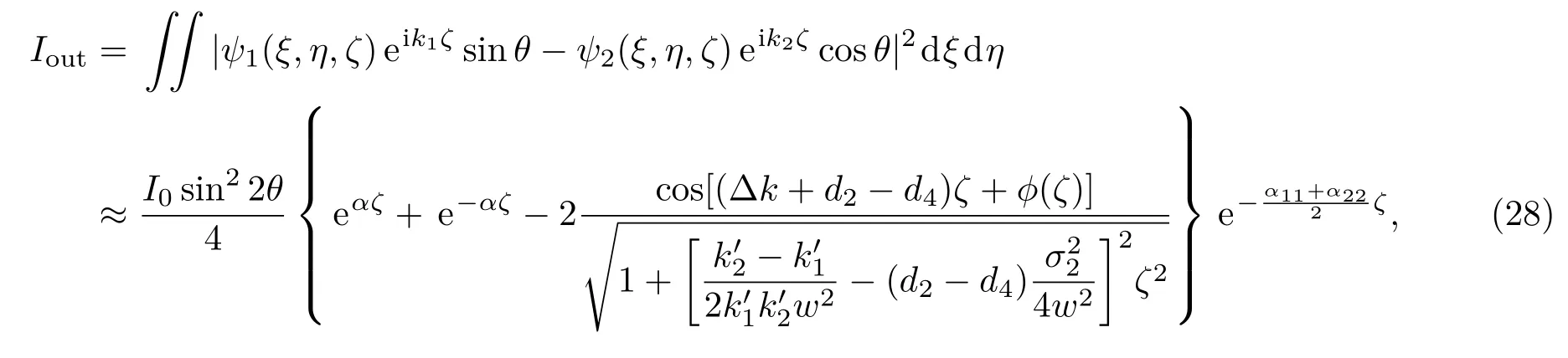
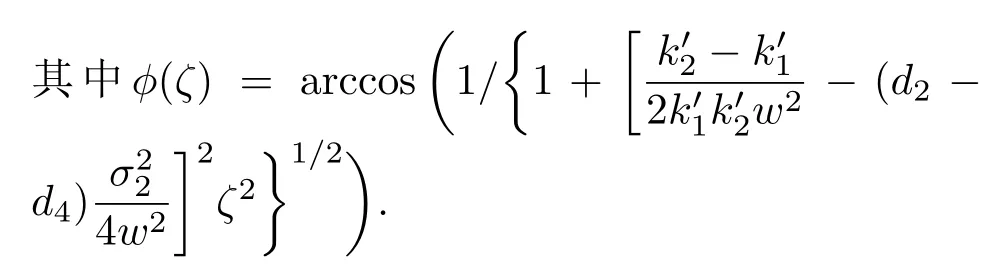
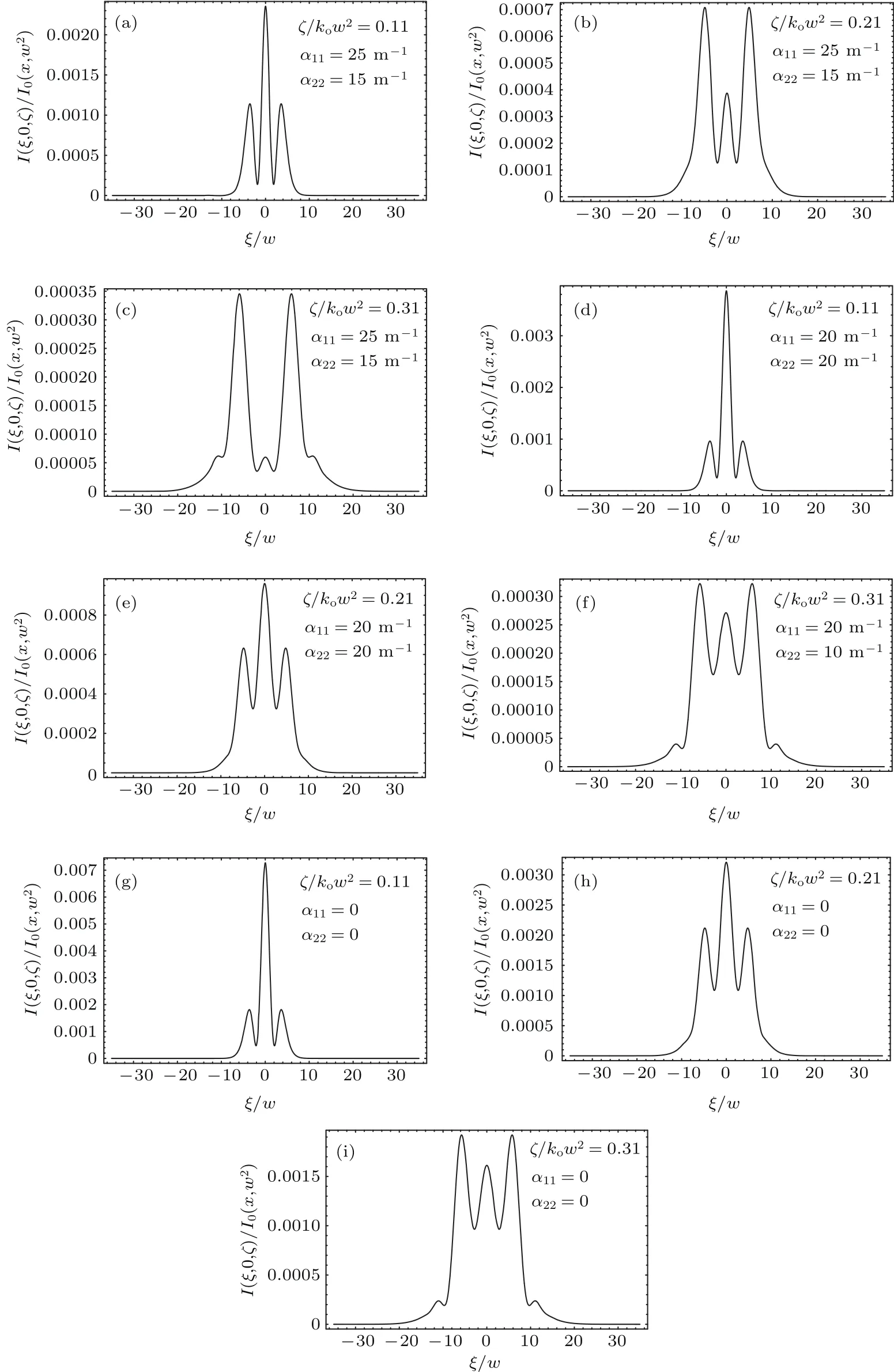
图2 当吸收系数α11和α22的值不同时,出射光I(ξ,0,ζ)/I0在不同的传播距离ζ/kow2处的光束形状,其中,k1=ko= 2.87770×107m−1,k2=ke=2.76460×107m−1,d2=192.076 m−1,d4=437.124 m−1Fig.2.Shapes of the output beam s I(ξ,0,ζ)/I0at diff erent travelling distancesζ/kow2w henα11andα22have d iff erent values.Here k1=ko=2.87770×107m−1,k2=ke=2.76460×107m−1,d2=192.076 m−1,d4=437.124 m−1.
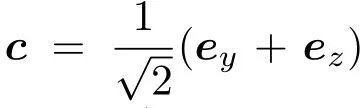
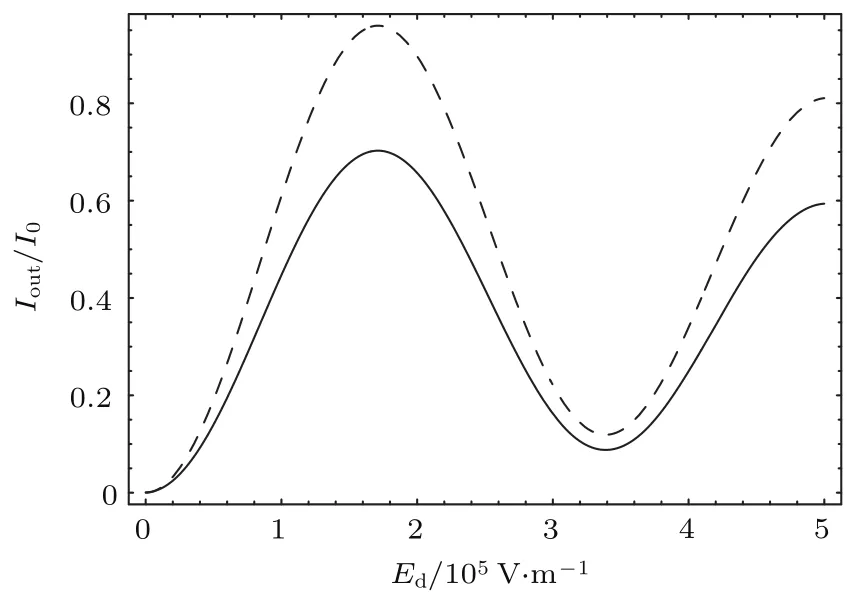
图3 出射光强度Iout/I0随外加电场Ed的变化,其中虚线α11= α22=0 m−1,实线α11=10 m−1, α22=15 m−1;其他参数的选取与图2相同Fig.3.The dependence of the ou tpu t intensity Iout/I0on the external dc electric field Ed. Dashed line: α11= α22=0 m−1;solid line,α11=10 m−1, α22=15 m−1.O ther param eters are the sam e as Fig.2.
注意到图2(d),(e),(f)中的光束形状(对应于α11= α22=20 m−1)与图2(g),(h),(i)中的光束形状(对应于α11=α22=0)分别对应相同,但图2(d),(e),(f)中的振幅由于吸收的存在发生了衰减.将图2中的(a),(b),(c)图分别与相应的图2(d),(e),(f)进行对比,同时结合(27)式可以发现,图2(a),(b),(c)由于α11̸= α22,出射光束的波形相对于图2(d),(e),(f)发生了改变.而且,由(27)式我们还注意到:在有吸收的介质中,当α11̸=α22时,即使没有非局域效应,入射时的高斯光束在晶体中传播一段距离后在晶体的出射面处波形也可能发生畸变而不再保持高斯光束波形.所以与无吸收介质中的情况不同,此处不能简单地根据出射光束波形的变化来判断¯χ(2)是否存在非局域响应.
仍然以LiNbO3晶体为例,根据(28)式给出了出射光强随外加电场变化的曲线,如图3所示.从(28)式和图3可以看出,电光振幅调制时,线性吸收使出射光的光强发生了衰减,调制的消光比减小,但调制的半波电压并没有受到明显的影响.这可为电光器件设计者提供参考.根据(28)式,给定各参数后,调节外电场Ed,当(Δk+d2−d4)ζ+ϕ(ζ)=π时,出射光强Iout达到最大值,此时有
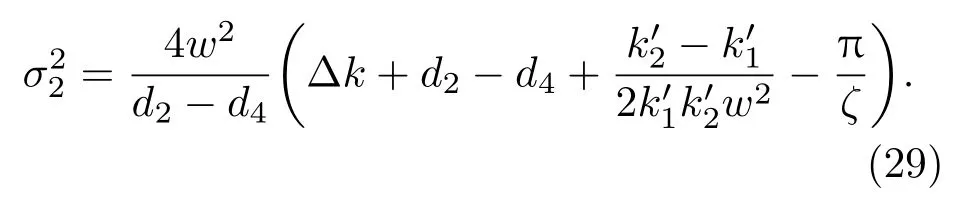
可以依据σ2的值是否为零,来判断¯χ(2)是否存在非局域响应.
4 结 论
我们进一步推广了线性电光效应的耦合波理论,提出了线性吸收介质非局域线性电光效应的耦合波理论.运用该理论,我们研究了线性吸收对非局域线性电光效应的影响.研究表明:首先,当α11=α22时,线性吸收使出射光场的振幅衰减,而不改变其波形.此时可以根据电光强度调制时出射光束波形是否保持为高斯型来判断是否存在非局域响应.其次,当α11̸=α22时,线性吸收除了使出射光场的振幅衰减还改变了其相位,从而导致电光强度调制时出射光束的波形发生变化,此时可通过测量σ2的值来判断¯χ(2)是否存在非局域响应.在α11̸=α22时,线性吸收还使电光强度调制的消光比减小,但对半波电压没有明显影响.最后,我们还讨论了测量和非局域响应特征长度和晶体吸收系数α11和α22的方法.
[1]Yariv A 1988Quan tum E lectronics(3rd Ed.)(New York: W iley)pp1–17,105–135
[2]van der Valk N C J,W enckebach T,P lanken P C M 2004 J.Opt.Soc.Am.B 21 622
[3]Chen L,Xu Q,W ood M G,Reano R M 2014 Optica 1 112
[4]Borshch V,Shiyanovskii S V,Li B X,Lav rentovich O D 2014 Phys.Rev.E 90 062504
[5]Zhang X,Chung C,Hosseini A,Subbaram an H,Luo J,Jen A K,Nelson R L,Lee C Y,Chen R T 2015 J. Lightwave Technol.34 2941
[6]W ang J,Li P,W eng S,W u L,Ning T,Li J 2016 Chin. Opt.Let.14 100603
[7]Liu K,Shi J,Zhou Z,Chen X 2009 Opt.Comm un.282 1207
[8]Gobert O,Paul PM,Hergott JF,Tcherbakoff O,Lepetit F,O liveira P D,V iala F,Com te M 2011 Opt.Express 19 5410
[9]Q ian S X,W ang G M 2002 Non linear Optics(1st Ed.) (Shanghai:Fudan University Press)pp334–343(in Chinese)[钱士雄,王恭明 2002非线性光学 (第一版)(上海:复旦大学出版社)第334—343页]
[10]Yariv A 1973 IEEE J.Quan tum E lect.9 919
[11]Nelson D F 1975 J.Opt.Soc.Am.65 1144
[12]Gunning M J,Raab R E 1998 Appl.Opt.37 8438
[13]She W,Lee W 2001 Opt.Comm un.195 303
[14]W u D D,Chen H B,She W L,Lee W K 2005 J.Opt. Soc.Am.B 22 2366
[15]Zheng G,She W 2006 Opt.Comm un.268 323
[16]Zheng G,W ang H,She W 2006 Opt.Express 14 5535
[17]Chen L,Zheng G,Xu J,Zhang B,SheW 2006Opt.Lett. 31 3474
[18]Huang D,She W 2007 Opt.Express 15 8275
[19]Tang H,Chen L,She W 2010 Opt.Express 18 25000
[20]W u D,She W 2016 Opt.Express 24 2867
[21]W ang G,W ang R 2013 Appl.Phys.Lett.102 021906
[22]Guo Q,Luo B,Y i F,Chi S,X ie Y 2004 Phys.Rev.E 69 016602
[23]K rolikow skiW,Bang O,Nikolov N I,Neshev D,W y ller J,Rasm ussen J J,Edm undson D 2004 J.Opt.Soc.Am. B 6 S288
[24]Haus H A 1984W aves and Fields in Optoelectronics(1st Ed.)(New Jersey:P rentice-Hall)pp81–157
[25]M itrofanov O,Gasparyan A,Pfeiff er L N,West K W 2005 Appl.Phys.Lett.86 202103
PACS:42.65.–k,42.70.M p,78.20.JqDOI:10.7498/aps.66.064202
W ave coup ling theory o f non local linear electro-op tic eff ect in a linear absorbent m ed ium∗
Wu Dan-Dan1)2)SheWei-Long1)†
1)(State K ey Laboratory of Op toelectronic M aterials and Technologies,Sun Yat-sen University,Guangzhou 510275,China)
2)(Physics Teaching and Experim ent Center,Sou th China University of Technology,Guangzhou 510006,China)
(Received 30 Sep tem ber 2016;revised m anuscrip t received 15 Novem ber 2016)
Being an im portant optical phenom enon,the linear electro-optic eff ect has diverse app lications in the opticalm odulation and op tical sw itching.The refractive index ellipsoid theory has been w idely used to study the linear electro-optic eff ect for a long time.Despite of its visualization such a theory has lim itations and cannot deal w ith a lot of cases in which the linear absorption cannot be neglected,or the electric disp lacem ent vector has a nonlocal response to electric field,etc.To overcom e such shortcom ings,in 2001 a wave coup ling theory of linear electro-optic eff ect was developed by She and Lee(She W,LeeW 2001 Opt.Comm un.195 303).And in 2016 we generalized this wave coup ling theory to the treatm ent of non local linear electro-optic eff ect in which the disp lacem ent vector has a non local response to electric field.
In this paper,we use this wave-coup ling theory to investigate how the linear absorption influences the linear electro-optic eff ect in a nonlocalm edium.Starting from M axwell’s equations and considering the linear absorp tion and the non locality of the susceptibility tensors,we obtain two coup ling equations for two orthogonal linear polarized waves and also analytical solutions of the resu lting equations,which can be used to describe the non local linear electro-optic eff ect for a light beam propagating along any direction,w ith an external direct current electric field app lied along an arbitrary direction in a linear absorbent crystal.W ith such solutions,we study the infl uences of the linear absorp tion on the phase,am p litude,shape of the output beam,aswellas the half-wave voltage and the extinction ratio of electro-optic m odulation.The results show that no m atter whether there exists linear absorp tion,the Rayleigh distance of the Gaussian beam in the crystalw ill be shortened as a result of the nonlocality of¯χ(1).W hen linear-absorption coeffi cientsα11andα22are equal,the linear absorption dam ps equally the am p litudes of the two polarized output beam s w ith keeping their phases and shapes unchanged.So in the case ofα11=α22,just as in a losslessm edium,the phenom enon that the output beam is no longer a Gaussian beam in an electro-optic am p litudemodu lation scheme can be considered as a possib le signal of the non local response of¯χ(2).M ore interestingly,whenα11̸=α22,the linear absorption not only reduces the am p litudes of output beam s,but also changes their phases and shapes.In such a case one need tomeasure the nonlocal characteristic length of¯χ(2)to judgewhether¯χ(2)has a nonlocal response.Finally,in the case ofα11̸=α22, as a result of linear absorption,the extinction ratio is reduced,but the half-wave voltage keeps nearly unchanged in an electro-optic am p litudemodulation scheme.Besides the discussion on the infl uence of the linear absorption,we also m ake suggestions of how to m easure the nonlocal characteristic lengths of¯χ(1)and¯χ(2)and the absorption coeffi cients α11andα22.
linear electro-optic effect,nonlocal,linear absorption,electro-opticmodulation
10.7498/aps.66.064202
∗国家自然科学基金(批准号:11274401)资助的课题.
†通信作者.E-m ail:shew l@m ail.sysu.edu.cn
*Pro ject supported by the National Natural Science Foundation of China(G rant No.11274401).
†Corresponding author.E-m ail:shew l@m ail.sysu.edu.cn

