2020年中国高等教育规模预测偏差成因分析及重估

胡顺顺，刘志民，2

（1.南京农业大学公共管理学院，江苏南京210095；2.江苏教育现代化研究院，江苏南京210013）

2020年中国高等教育规模预测偏差成因分析及重估

胡顺顺1，刘志民1，2

（1.南京农业大学公共管理学院，江苏南京210095；2.江苏教育现代化研究院，江苏南京210013）

2010年公布的《国家中长期教育改革和发展规划纲要（2010-2020年）》明确提出：“到2020年，高等教育毛入学率达到40%。”但是，教育部最新统计数据显示，我国2015年的高等教育毛入学率已经提前5年超前实现了40%的目标。为什么会出现如此大的偏差？结合对各学者预测内容的梳理，笔者认为原因主要有三：一是信息更新约束与模型差异；二是理性偏误；三是不可预测的政策因素。在连续毛入学率预测数据中，预测误差较小的学者使用了Logistic模型、GM（1，1）灰色预测模型及高等教育规模滚动回归模型。本文使用方差-协方差组合预测法，辅以改进后的三种模型来重新估计2020年高等教育毛入学率。结果显示，2020年我国高等教育毛入学率将达到且超过50%。

高等教育；规模；预测偏差；组合预测

一、引言

进行高等教育规模的预测研究，掌握高等教育未来招生规模、在校生规模及毕业生规模的变化趋势，可以更好地把握未来高等教育的发展趋势，制定具有前瞻性的教育规划，从而促进我国从教育中等发展水平国家向教育发达国家的转变。因此，高等教育规模预测的结果对未来高等教育的发展起到了重要的指导作用。2010年公布的《国家中长期教育改革和发展规划纲要（2010-2020年）》（以下简称《规划纲要》）明确提出：“到2020年，实现更高水平的普及教育，高等教育大众化水平进一步提高，毛入学率达到40%。”但是，教育部最新统计数据显示，我国2015年的高等教育毛入学率已经超前实现40%的目标。这一规模的实现比发展规划提前了5年，这是一个喜讯。而值得反思的是，为何预测目标会产生如此大的偏误？《规划纲要》在制定前后，有关专家学者是如何对高等教育规模进行预测的？

在十二届全国人大四次会议记者会上，原教育部部长袁贵仁提出了“到2020年，我国的高等教育毛入学率应当达到50%”的新目标[1]，这也就意味着未来五年内我国的高等教育毛入学率要继续增长10%，达到高等教育普及化阶段的毛入学率目标。新目标比40%更具挑战性，因为在普及化教育阶段，非选拔性的高等教育对所有想读大学的人开放，它与现实的各种社会需求的联系更加密切，而非只是量的变化。本研究通过对2003-2015年部分学者对高等教育规模的实证预测进行梳理，对比其预测方法、变量选择、数据来源以及预测结果，初步分析其预测偏差原因。然后，使用方差-协方差组合预测法，辅以改进后的三种模型，对高等教育规模进行最新预测。

二、学者对高等教育规模的预测及其误差

《规划纲要》公布前后，众多学者对我国中长期高等教育规模进行了多种预测，使用了各种模型、数据与方法，预测的结果有所差别。如表1所列举的16篇文章中，若以相差5%（绝对值）为误差边界，则有超过2/3（69%）的预测结果是存在误差的。

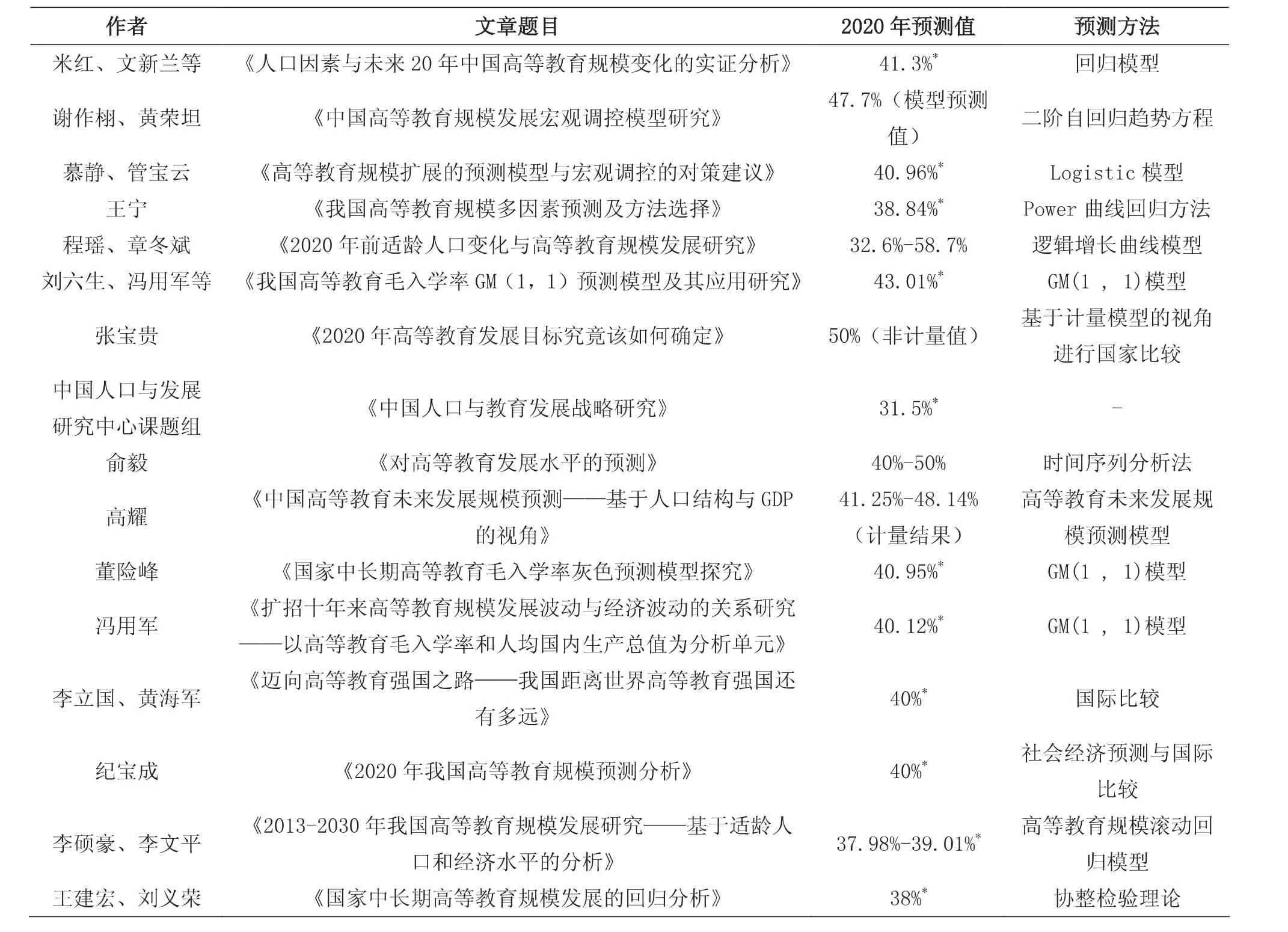
表1 部分学者对2020年高等教育毛入学率的预测结果及方法

接下来，我们将对学者的预测值与实际值进行比较，进行描述性统计分析，从而简单地判断他们预测的误差程度。因有些文章仅对2020年的高等教育毛入学率进行预测，没有连续的预测数据，本文仅对通过定量方法得出的连续的预测值进行比较，比较结果如图1。

图1 部分学者预测值与实际值比较（黑色为实际值）

由图1可以看出，在连续的高等教育预测数据中，学者们的预测具有相关性，且在2017-2018年左右高度重合。通过进一步比较可以得出这些学者的预测数据与实际数据（2010-2015年）的误差值，如表2所示。

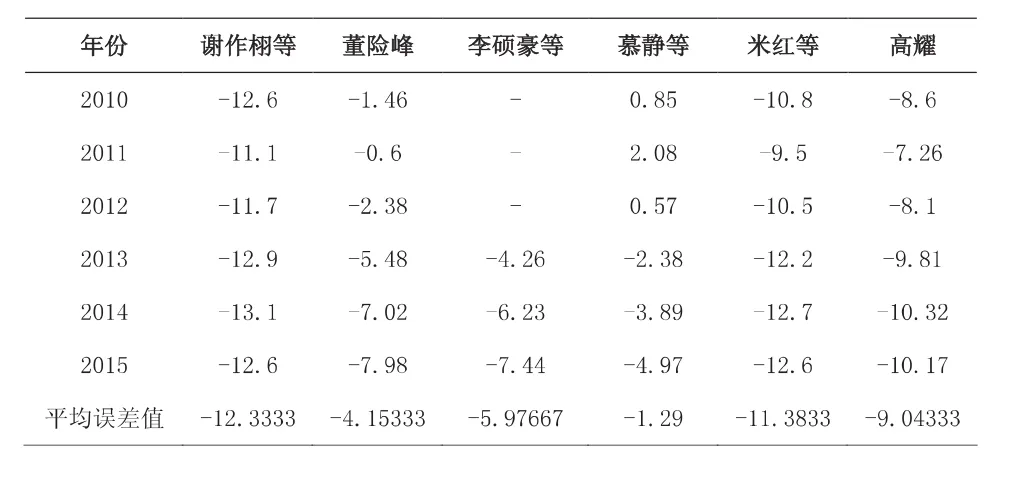
表2 部分学者预测值与实际值（2010-2015年）的误差值

从表2的平均误差值来看，学者们的误差表现呈现两极分化：平均误差最大达到12.3，最小只有1.29。在2010年和2012年，慕静等人的预测误差值均小于1。

三、产生偏差的原因探讨

《规划纲要》颁布前，有很多学者的预测值与其相近。笔者认为，这为《规划纲要》中“40%”目标的确立提供了理论支持及借鉴。因此，分析各学者预测偏差的原因，有助于提高重估的准确性。

理论上说，预测产生误差几乎是具有必然性的。对此也有两类解释。其一是信息更新约束下的理性预期假说。Mankiw和Reis认为，经济信息的扩散是缓慢的，信息的收集与处理成本导致粘性信息或不完美信息。由于预测者在获取和处理新信息时需要一定的成本，预测者最优的信息更新策略是进行定期更新，而不是连续收集和处理新信息，从而产生了粘性信息，使得每一期都只有一定比例的预测者更新信息[2]。其二是理性偏误假说。这一假说认为，预测本身是一种产品，预测数据的供需双方出于理性上的考虑，选择更有利于自身的预测[3]。能够影响预测数据的主体主要有政府、企业、消费者及预测者自身[3][4][5]。此外，不同的模型、基础数据和临界年的选择等都可以成为影响预测精度的重要因素。

（一）信息更新约束与模型差异

最新信息的收集与处理是预测质量的重要保证。在信息市场不对称的情况下，信息收集者对想要得到的信息有时并不能完全获取，抑或是因为疲于更新连续信息，使得粘性信息或不完美信息被应用到模型中，从而导致预测偏差。如果对同一个变量做多次预测，随着时间的推移及信息的更新，预测均值的偏差会逐渐缩小。结合学者们的实际使用数据来看，表3描述了部分学者选择数据的临界年区间。其中，米红等[6]和高耀[7]在相关研究中所使用的数据并非当时的最新数据。由于信息更新约束所带来的数据年限差异是无法避免的，每一个数据的加入或减少都会对预测结果产生影响，所以最新信息的使用能够使预测结果更显真实。然而，Batchelor和Dua[8]发现预测者在得到最新数据后，往往并未表现出积极的使用欲望。如李硕豪等[9]在文章中所使用的高等教育毛入学率数据在发表前两个多月已可收集，但作者并未及时更新。①另一方面，如果预测者所使用的最新数据表现出的趋势从长期来看并不具有代表性，这也会给预测值的准确性带来很大影响。比如，我国高等教育毛入学率在2005-2011年间的年均增长率只有0.98%，但此后增长率便大幅度提高，年均增长率达到了3.28%。这种从一段时间的缓慢增长快速转变为高速增长的现象，通过计量模型是很难预测的。

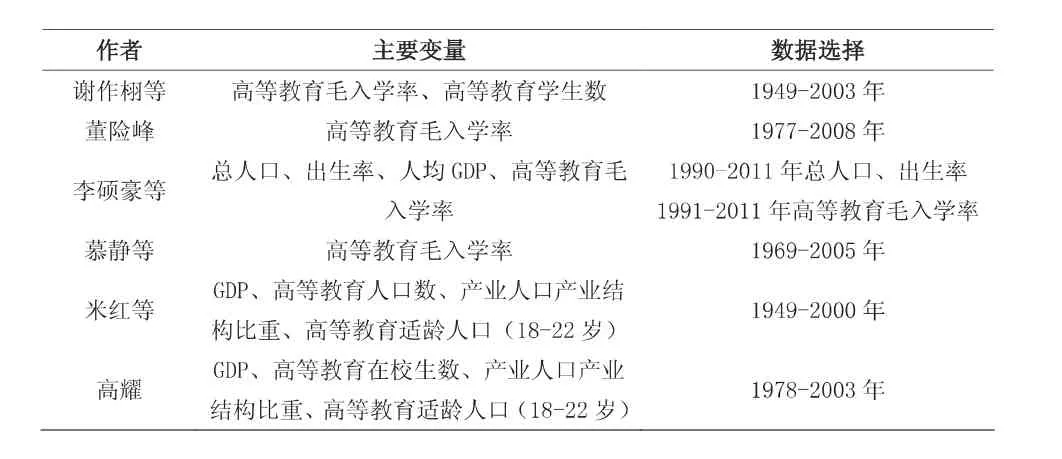
表3 部分学者预测变量及数据的选择

预测准确性的关键更表现为是否有好的理论模型[10]。预测模型与方法多种多样，主要分为传统的预测方法和新兴的预测方法[11]。传统的预测方法主要有回归分析模型、时间序列模型及生产函数模型等，使用者如米红等[6]、王宁[12]和俞毅[13]。这类方法需占有丰富、翔实的历史数据统计资料，并且要求数据变化过程表现出一定的规律性。然而，回归分析模型也有其固有缺陷，回归模型对环境变化的适应能力较差，无法在经济社会形势发生快速变化的条件下得出理想的预测结果，而且使用此方法时往往需要充分利用近期统计数据。如米红等[6]学者的预测结果，其连续预测数据的平均误差值达到了-11.38。新兴的预测方法近年来发展很快，目前应用得较为成熟的主要有灰色系统理论预测模型、BP神经网络模型以及仿真模型等。灰色系统理论预测模型应用较广，已有董险峰[14]、冯用军[15]等学者使用灰色系统理论中的GM（1，1）模型进行预测。但是，有学者提出，原GM（1，1）灰色预测公式在进行最小二乘法计算时，默认X（1）（1）=X（0）（1），但是曲线并不一定经过这一点，使得预测结果产生系统偏差[16]。如董险峰[14]的预测结果在2011年差距达到最小，之后逐年扩大。

（二）理性偏误假说

理性偏误假说主要分为声誉因素和迎合政府需要假说两个方面。声誉是决定预测者市场的重要因素，在不完全信息下，预测者的声誉不仅取决于预测的准确性，还与其他人的预测有关，由此，可能出现“随大流”和“标新立异”两种截然不同的预测策略[17]。“随大流”是一种比较常见的做法，在本次研究的文献中，多体现“随大流”的预测。如上文分析的6篇具有连续预测数据的文章，其预测结果相关系数r高达0.996。尽管这样笼统计算出的相关系数带有自相关性等问题，但也能大致看出，各学者预测结果存在“随大流”现象。尤其是在2020年的预测结果上，2010年后的诸多学者通过各种方法预测的结果多为40%。在一个预测能力没有显著差异的预测市场上，规避风险的预测者倾向于选择趋同预测来降低预测错误时的声誉损失[5]。迎合政府需要假说是在理性上遵循国家意志的一种表现，该假说原被用来解释经济指标的预测偏差，如Heinemann[3]用其解释德国官方机构对税收收入的长期高估。我国的高等教育是中央和地方二级管理体制，以地方管理为主，同时政府也是高等教育机构经费的主要来源[18]。因此，具有官方背景的学者们很可能会理性地选择迎合政府的主张。分析表1所列的15篇文章（中国人口与发展研究中心课题组报告除外）可以发现，明确将预测结果与《规划纲要》或官方政策规划相比较的有9篇文章，占总数的60%，如表4所示。

表4 预测结果与相比较的政策规划

（三）不可预测的政策因素

政策的变动对我国教育发展影响巨大。对于高等教育规模来说，影响最大的一次政策调整莫过于1999年以来的大规模扩招，这一持续的大规模的扩招使得我国高等教育毛入学率大幅度上升，这种增幅是无法用模型来解释的[6]。有学者将其总结为高等教育大扩招的惯性和地方政府释放压抑多年的高等教育发展张力，虽有国家政策的宏观调控，但社会经济的持续快速发展（公民高等教育支付能力显著增强）、国民高涨的高等教育需求加上地方政府部门的政绩期望，使得这种扩招惯性和张力有增无减[14]。

其次，我国高等教育在学规模的统计口径调整，也是影响预测精度的重要因素。1993-1998年，我国高等教育在学总规模是普通高校的学生数和成人高校的学生数之和[19]。1999年，修改为高等学校和科研机构的在学研究生数、普通高等学校各种类型本专科学生数、成人高等学校本专科学生数、军事院校本专科学生数、学历文凭考试专科学生数、电大视听生注册人数折算系数、高等教育自学考试毕业生人数折算系数等7项的总和[20]。2015年8月，修改为普通高等教育本专科在校生数+研究生在校生数+成人本专科折合在校生数（成人脱产班在校生数+成人夜大在校生数×0.5+成人函授在校生数×0.5）+网络本专科在校生数×0.5+自学考试毕业人数×1.5+在职攻读学位研究生在学人数+研究生课程进修班在学人数×0.5+军事院校本专科在校生数[21]。从口径变化来看，计算公式趋于合理，但计算类别不断增加，这也为我国持续高速增长的高等教育规模数据提供了统计学解释。

此外，受人口出生率持续下降等因素的影响，2016年我国出台了“全面二孩政策”。据有关学者调查，政策出台后，我国将面临2000万左右的新增人口[22]。至少现在看来，这对于优质高等教育招生资源日渐饱和的中国来说，无疑是一个新的挑战。

四、高等教育规模预测

（一）单一模型设计与计量结果

1.单一模型设计

通过文献分析及描述性统计发现，在众多预测结果中，最接近实际值的学者依次使用了Logistic模型、GM（1，1）灰色预测模型和高等教育规模滚动回归模型。单个模型，尤其是一元模型数据单薄，囿于教育系统内的发展规律，即使预测偏差较小，也缺乏与社会经济系统的联系。相比之下，多因素的高等教育规模预测模型虽然加入了社会经济变量，考虑得也较为周全，但在预测结果上差强人意。因此，本文将在三个模型改进的基础上，使用方差-协方差组合预测法对高等教育规模进行重估，尽可能权衡预测结果之间的差距，以得出更精确的预测结果。做法是分别对Logistic模型、GM（1，1）灰色预测模型和高等教育规模滚动模型进行改进预测，最后根据三者的预测结果，使用方差-协方差组合预测法得出最终预测结果。为了检验组合模型和其他模型的预测结果，将2011-2015年的高等教育毛入学率作为测试数据，如表5所示。

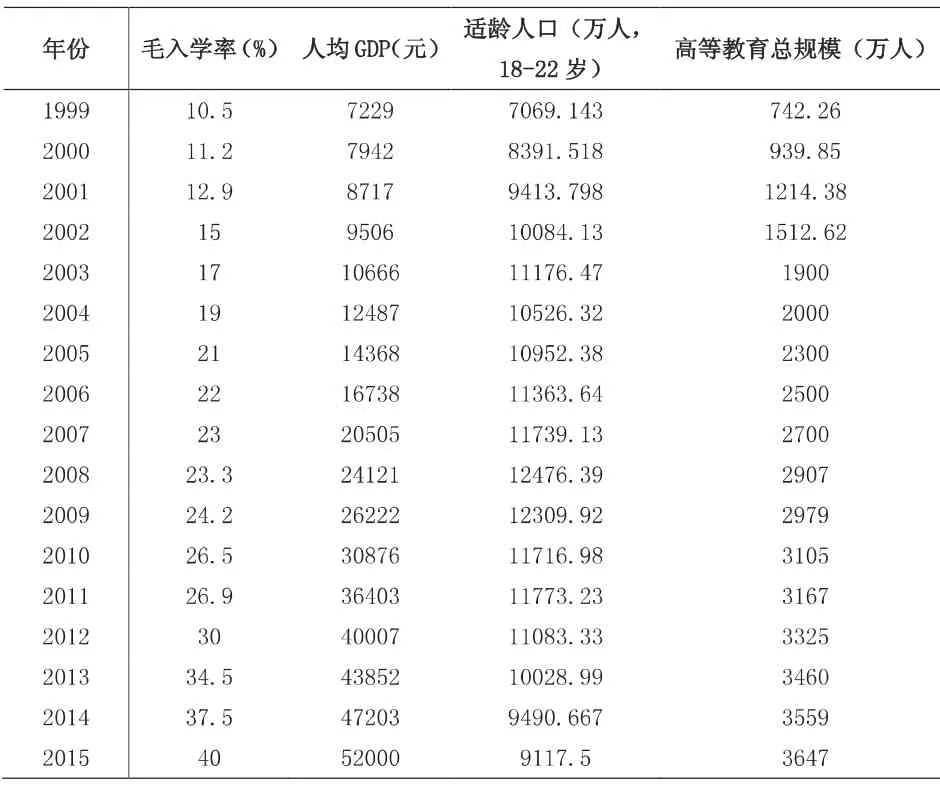
表5 1999-2010年经济、人口与高等教育各项数据

Logistic模型是常见的时间序列预测模型，本文通过非线性参数预测的方法以1978-2010年的毛入学率数据为基础，拟合Logistic模型如表6。GM（1，1）灰色预测模型具有要求数据少、不考虑分布规律和变化趋势、运算方便等优点。通过使用高等教育大扩招之后的1999-2010年的高等教育毛入学率数据，以反映不经干预和调控优化的客观趋势。

高等教育规模滚动预测模型可以在控制变量回归系数变异的基础上，减小估计误差，从而缩减回归方程的预测年限。以5年作为一个预测单位滚动修正回归模型，并将高等教育在学人数结果与社会经济系统进行回归拟合，把高等教育毛入学率纵向历史数据发展规律与横向人口、经济因素相联系，增加模型可靠性。具体做法是使用1999-2010年和1999-2015年的人均GDP、高等教育适龄人口以及高等教育在校生数据拟合出回归方程1和方程2，使用方程1预测2011-2015年的高等教育规模，使用方程2预测2016-2020年的高等教育规模，方程1的结果用来检验模型预测精度。人均GDP既能衡量一国的经济发展水平，又能在一定程度上反映一国居民在生活、教育等方面的支付能力，直接影响学生的入学选择，与高等教育规模的联系更加紧密。虽然现阶段我国已经实施了“全面二孩”政策，但是首批人口增量在18年后才会出现，所以高等教育适龄人口数在短期内不会有较大变化。因此，本文选取人均GDP和高等教育适龄人口数两个变量加入高等教育滚动回归模型。经过计算，三种方法的预测模型如表6所示。

表6 高等教育规模预测模型表达式

2.计量结果

使用改进后的三种模型对我国2011-2015年高等教育毛入学率进行预测，结果如表7所示。

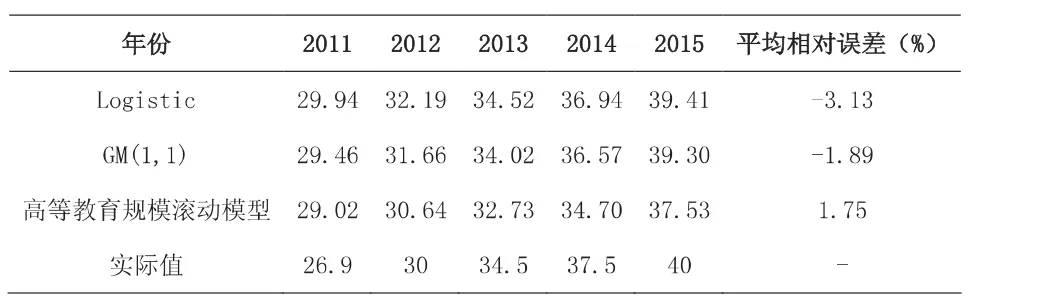
表7 高等教育规模模型预测结果

根据表7的预测结果，每种模型的预测结果存在一定差距。为了得出更精确的结果，本文选用组合预测方法。组合预测是综合各种单项预测方法的结果而建立起来的一种预测方法，首先需要对每个预测模型赋予不同的权重，对比较精确的预测值赋予比较大的权重。这样做可以降低单一模型中的预测误差，也提高了预测精度。

（二）方差-协方差组合预测法的设计与结果

1.方差-协方差组合预测法设计

假设三种预测结果的组合关系为：

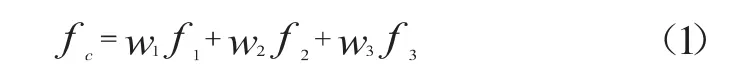
式中f1、f2、f3为三种单一模型的预测值；fc为加权平均的组合预测值；w1、w2、w3为相应的权系数，且w1+ w2+w3=1。

设三个单一模型预测误差分别为e1、e2、e3，组合预测误差为ec，方差为D（ec），对应的表达式分别为：

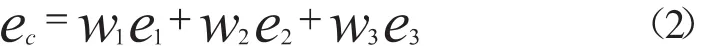
由于三种模型的结果是相互独立的，所以其方差可表示为：

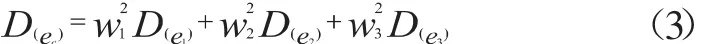
求wi（i=1，2，3）的最小值，可以引入拉格朗日乘子求得，三种预测方法的组合预测权系数分别为：

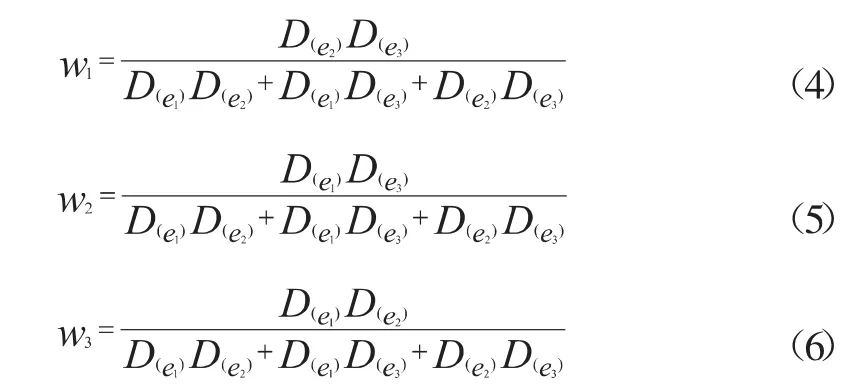
从式（4）中不难看出：

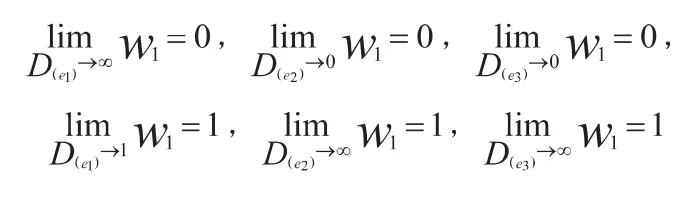
由此可以得出结论：第一种模型的权数值与该预测值的误差成反比。依此类推。

2.方差-协方差组合预测结果

根据以上公式，结合表5和表7数据，可计算出w1= 0.3633，w2=0.4118，w3=0.2249。由此可求得组合预测的结果，如表8所示。

结合表7与表8的相对误差可知，方差-协方差组合预测的平均相对误差值为1.52%，相比于其他预测值，预测效果更好。接下来，使用该方法计算的权系数对2016-2020年的高等教育毛入学率进行预测，预测结果如表9所示。

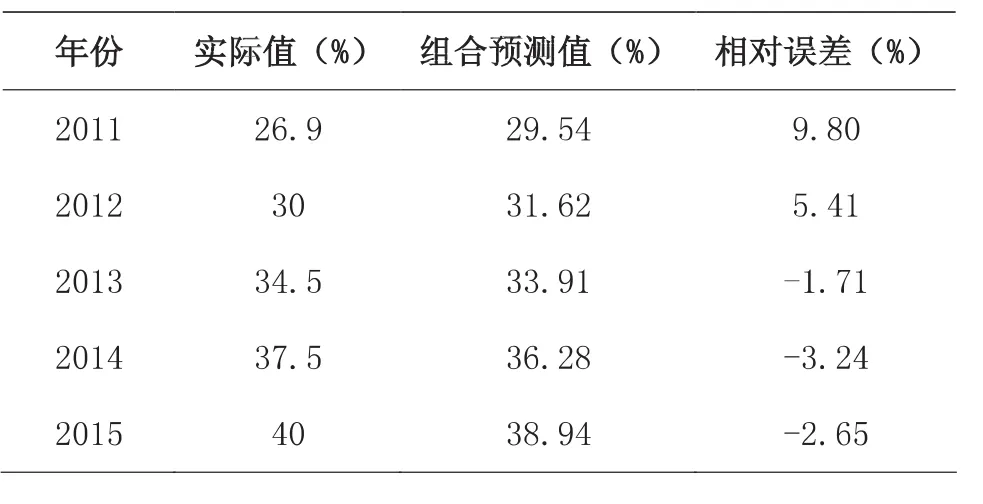
表8 方差-协方差组合预测

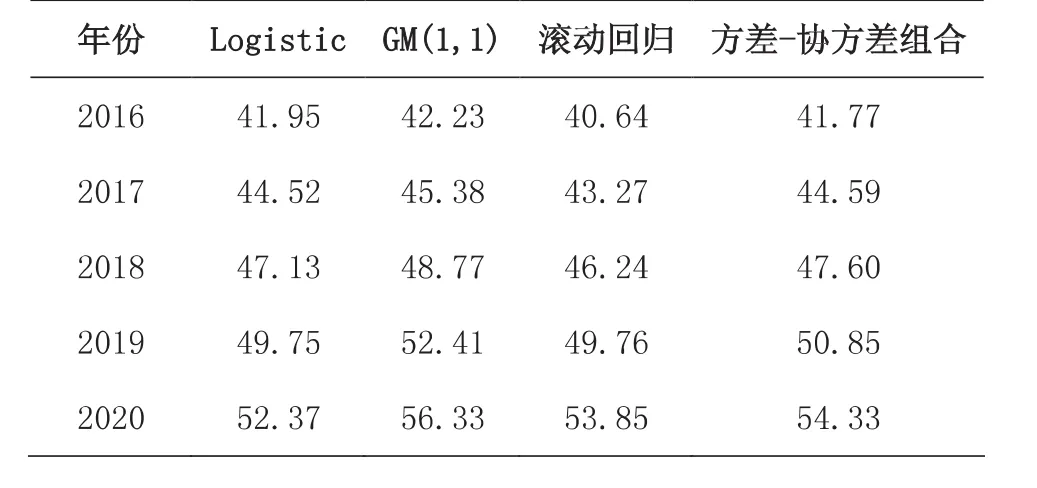
表9 2016-2020年高等教育毛入学率预测

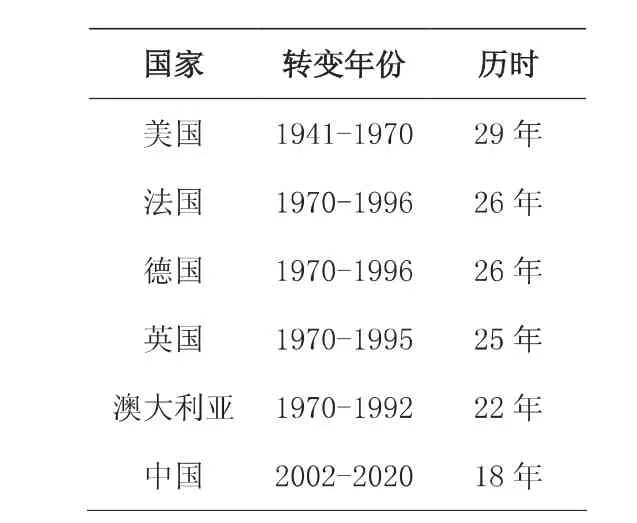
表10 世界主要发达国家高等教育由大众化向普及化转变的时间对比

五、结论与反思

从计量的结果看，我国高等教育毛入学率在2020年有可能会达到或超过50%。如若预测结果能够实现，那么与世界发达国家高等教育规模发展速度相比，我国的高等教育规模发展速度将名列前茅，如表10所示。但是，高等教育规模高速发展带来的弊端是高等教育质量与规模发展不协调。

在当前形势下，高等教育规模扩张过快带来的高等教育质量滑坡、学科建设趋同、经费投入不足、毕业生就业难、教师队伍建设滞后等多重问题仍然存在[23]。但是，我国高等教育现在还没有达到普及化阶段，只能适度增长，不能停止，即“逆水行舟，不进则退”[24]。笔者建议，放慢规模发展步伐，发展重心转移至质量方面，“稳步低速增长，是我国高等教育规模发展的较好选择”[25]。

注释

①《2012年全国教育事业发展统计公报》公布于2013年8月16日，其中包含高等教育毛入学率数据；而相关文章发表于2013年12月，且修回日期为2013年11月1日。

[1]人民网.教育部长袁贵仁就“教育改革和发展”答记者问[EB/OL].（2016-03-20）[2016-10-09].http：//live.people.com.cn/note.php?id= 1113160308164232_ctdzb_001.

[2]MANKIW N G，REISR.Sticky Information Versus Sticky Prices：A Proposal to Replace the New Keynesian Philips Curve[J].Quarterly JournalofEconomics，2002，117（4）：1295-1328.

[3]HEINEMANN F.Planningor Propaganda?An Evaluation ofGermany's Medium Term Budgetary Planning[J].Finanzarchiv Public Finance Analysis，2006，62（4）：551-578.

[4]ITO T.Foreign Exchange Rate Expectations：Micro Survey Data[J]. American Economic Review，1990，80（3）：434-449.

[5]LAMONT O.Macroeconomic forecasts and microeconomic forecasters [J].Journal of Economic Behavior and Organization，2002，48（3）：265-280.

[6]米红，文新兰，周仲高.人口因素与未来20年中国高等教育规模变化的实证分析[J].人口研究，2003（6）：76-81.

[7]高耀.中国高等教育未来发展规模预测——基于人口结构与GDP的视角[J].管理学刊，2010（3）：70-73.

[8]BATCHELORR，DUA P.Conservatism and consensus-seekingamong economic forecasters[J].Journalof Forecasting，1992，11（2）：169-181.

[9]李硕豪，李文平.2013－2030年我国高等教育规模发展研究——基于适龄人口和经济水平的分析[J].开放教育研究，2013（6）：73-80.

[10]田成诗，朱佳宝.我国省域人口的时序预测模型的选择——基于预测精度、偏差和不确定性的分析[J].数学的实践与认识，2014（12）：157-169.

[11]李涛，宋光新.区域人才资源需求预测方法研究[J].云南财经大学学报，2006（6）：91-94.

[12]王宁.我国高等教育规模多因素预测及方法选择[J].高教探索，2008（6）：39-44.

[13]俞毅.对高等教育发展水平的预测[J].当代教育论坛，2010（7）：60-62.

[14]董险峰.国家中长期高等教育毛入学率灰色预测模型探究[J].国家教育行政学院学报，2010（5）：43-47.

[15]冯用军.扩招十年来高等教育规模发展波动与经济波动的关系研究——以高等教育毛入学率和人均国内生产总值为分析单元[J].中国高教研究，2010（9）：11-14.

[16]张大海，江世芳，史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002（8）：140-142.

[17]夏纪军，康健.中国宏观经济预测偏误研究[J].管理世界，2009（11）：21-28.

[18]熊庆年.过度竞争有损高等教育公平[N].社会科学报，2017-03-16（4）.

[19]易梦春.我国高等教育普及化进程及其影响因素——基于时间序列趋势外推模型的预测[J].中国高教研究，2016（3）：47-55.

[20]杨晓青.如何计算高等教育毛入学率[J].中国高等教育，2003（10）：36.

[21]教育部.教育部关于印发《中国教育监测与评价统计指标体系》的通知[EB/OL].（2015-08-18）[2017-03-23].http：//www.moe.edu. cn/srcsite/A03/s182/201509/t20150907_206014.htm l.

[22]乔晓春.实施“普遍二孩”政策后生育水平会达到多高?——兼与翟振武教授商榷[J].人口与发展，2014（6）：2-15.

[23]杨晓青.高等教育规模发展的影响因素分析[J].教育发展研究，2007（23）：24-28.

[24]潘懋元.关于《国家中长期教育规划纲要（2010-2020）》的理解与实践问题[J].集美大学学报，2010（7）：1-6.

[25]瞿振元.高等教育强国：本质、要素与实现途径[J].中国高教研究，2013（3）：1-5.

On the Sources of Bias in the Prediction of China's Higher Education Scale in 2020 and Its Re-evaluation

HU Shun-shun1，LIU Zhi-min1，2
（1.College of Public Administration,Nanjing Agricultural University,Nanjing 210095,Jiangsu,China；2.Institute of Education Modernization,Nanjing 210013,Jiangsu,China）

China's National Plan for Medium and Long-term Education Reform and Development(2010-2020)proposes a strategic goal that China's gross enrollment rate of higher education will reach 40%by 2020. However,new statistics show that China has achieved the long-term development goals of higher education in 2015,five years in advance.Based on the literature review,the paper identifies threemain reasons for the bias of predications,i.e.the constraints of information updating and model difference,the rational bias and the unpredictable policy factors.In some forecast variables of the continuous gross enrollment rate,more accurate predictions are achieved by employing Logistic model,GM(1,1)model and rolling regression model.By a combination of variance-covariance prediction method and the aforementioned three models,the paper shows that China's higher education gross enrollment ratewill reach 50%in 2020.

Higher Education；Scale；Predicating Bias；Combination Forecasting

2016-12-01

江苏省重点培育智库教育现代化研究院2017年短期项目（ZK_D/2017/02）

胡顺顺，1992年生，男，安徽阜阳人，南京农业大学公共管理学院硕士生，从事教育经济研究；刘志民，1960年生，男，陕西临潼人，南京农业大学公共管理学院教授、博士生导师，高等教育研究所所长，江苏教育现代化研究院教育与经济社会发展研究所所长，从事教育经济与战略研究。