计入运动副间隙的汽车制动摆振动态响应分析

姜俊昭 卢剑伟 李金辉 杨士钦

1.合肥工业大学汽车与交通工程学院，合肥，2300092.江淮汽车股份有限公司乘用车技术中心，合肥，230601



计入运动副间隙的汽车制动摆振动态响应分析

姜俊昭1卢剑伟1李金辉1杨士钦2

1.合肥工业大学汽车与交通工程学院，合肥，2300092.江淮汽车股份有限公司乘用车技术中心，合肥，230601

建立了考虑制动过程中参数时变特性，并计入转向系运动副间隙耦合作用的七自由度非自治摆振系统的动力学模型。通过MATLAB数值算例，对制动过程中转向轮摆振的动态响应进行了分析。考察了轴荷转移、车速、间隙、轴距等因素对系统瞬态响应的影响。研究结果表明：制动过程中，轴荷转移等时变特性及运动副间隙的耦合作用对摆振系统动力学行为有重要影响，在建模时应予以考虑。相关规律与试验结果基本吻合，验证了模型的准确性。

摆振；制动；间隙；轴荷转移；瞬态响应

0 引言

汽车制动时，转向轮摆振是一种较为常见的现象。转向轮摆振会引起转向机构动载荷的增加，加剧轮胎以及转向系统零部件的磨损，严重时会对车辆的制动性、操纵稳定性、行驶安全性等产生不良影响[1-2]。

以往的理论与试验研究表明：制动过程中，制动器制动力矩波动与制动力不平衡会引起制动力的周期性变化，从而给转向系激励，导致汽车制动时发生摆振[3-4]。这类摆振属于强迫振动，机理明确，例如制动鼓失圆、制动鼓与轮辋的同轴度不良均会引起制动力不平衡。自激型摆振则不需要周期性的激励源，它依靠自身调节，把外部能源转换成能够产生周期性激振力的能量[5-6]，因此这类摆振在制动力矩平衡的情况下也会发生。汽车制动时，转向系统敏感度的高低[7]、轴荷转移、轮胎侧偏和纵滑的动态变化可能会改变自激型摆振的瞬态响应，影响汽车的操纵稳定性，但是这方面的研究尚不够深入。另外，工程实践中，在役车辆由于运动副磨损而导致其摆振响应加剧的现象较为常见。笔者发现间隙的存在扩大了摆振现象发生的车速区间，一些原先对车辆摆振响应不敏感的参数也会变得敏感[8-9]。摆振的发生通常表现为系统中多个部件间的耦合动力学问题[10]，因此，有必要对考虑制动过程中技术参数的时变特性及其与转向系运动副间隙等部件的耦合作用的摆振系统动力学行为进行讨论。

基于上述分析，本文以某国产车型参数为基础，建立了考虑制动过程中的参数时变特性，并计入转向系运动副间隙耦合作用的七自由度非自治摆振动力学模型，依据Hertz接触理论，描述了多个运动副间隙的受力情况。根据样车轮胎六分力试验数据，通过设计参数辨识算法对考虑侧偏纵滑的复合工况轮胎模型进行了数据拟合，精确描述了ABS制动过程中的轮胎侧偏纵滑时变特性。通过MATLAB数值算例，仿真分析了制动过程中摆振的动力学响应，考察了轴荷转移、车速、间隙、轴距等参数对系统瞬态响应幅值或瞬态响应时间的影响。相关规律与试验结果基本吻合，验证了模型的准确性。

1 汽车摆振动力学分析模型

同时考虑转向传动机构中横拉杆和左右梯形臂之间的两个运动副间隙的摆振系统如图1所示。图2为整车横摆结构示意图。整个系统包含7个自由度：左前轮绕主销的摆角θ1、右前轮绕主销的摆角θ2、前桥绕纵轴线的侧摆角ψ、横拉杆横摆角Φ、横拉杆质心S1沿x方向的位移Xs、横拉杆质心S1沿y方向的位移Ys、汽车横摆角速度ω。

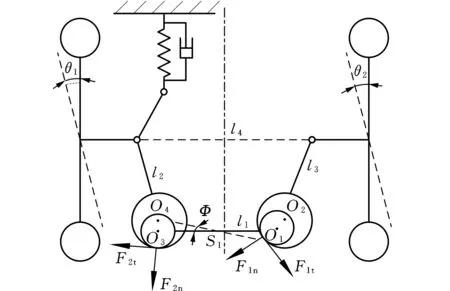
(a)俯视图

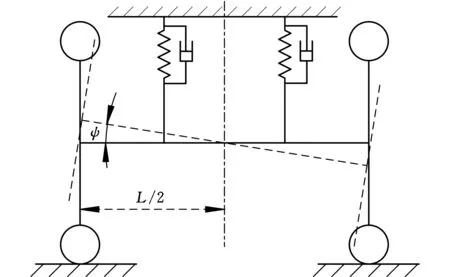
(b)后视图图1 考虑多个运动副间隙的车辆摆振系统示意图Fig.1 Diagram for vehicle shimmy system with consideration of multi-clearance joints

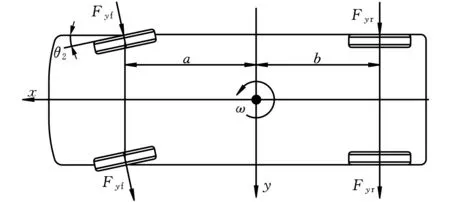
图2 汽车横摆示意图Fig.2 Diagram for vehicle yaw

1.1 间隙运动副描述

为受力分析方便，对左转向梯形臂与横拉杆之间的运动副间隙进行放大，如图3所示。结合图1可知，O1、O2分别为右侧轴销与轴套的中心，O3、O4分别为左侧轴销与轴套的中心。基于Hertz接触理论描述间隙运动副的受力，计入运动副元素接触表面的弹性、阻尼、摩擦等，间隙运动副接触点的法向力为

(1)

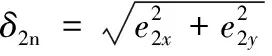
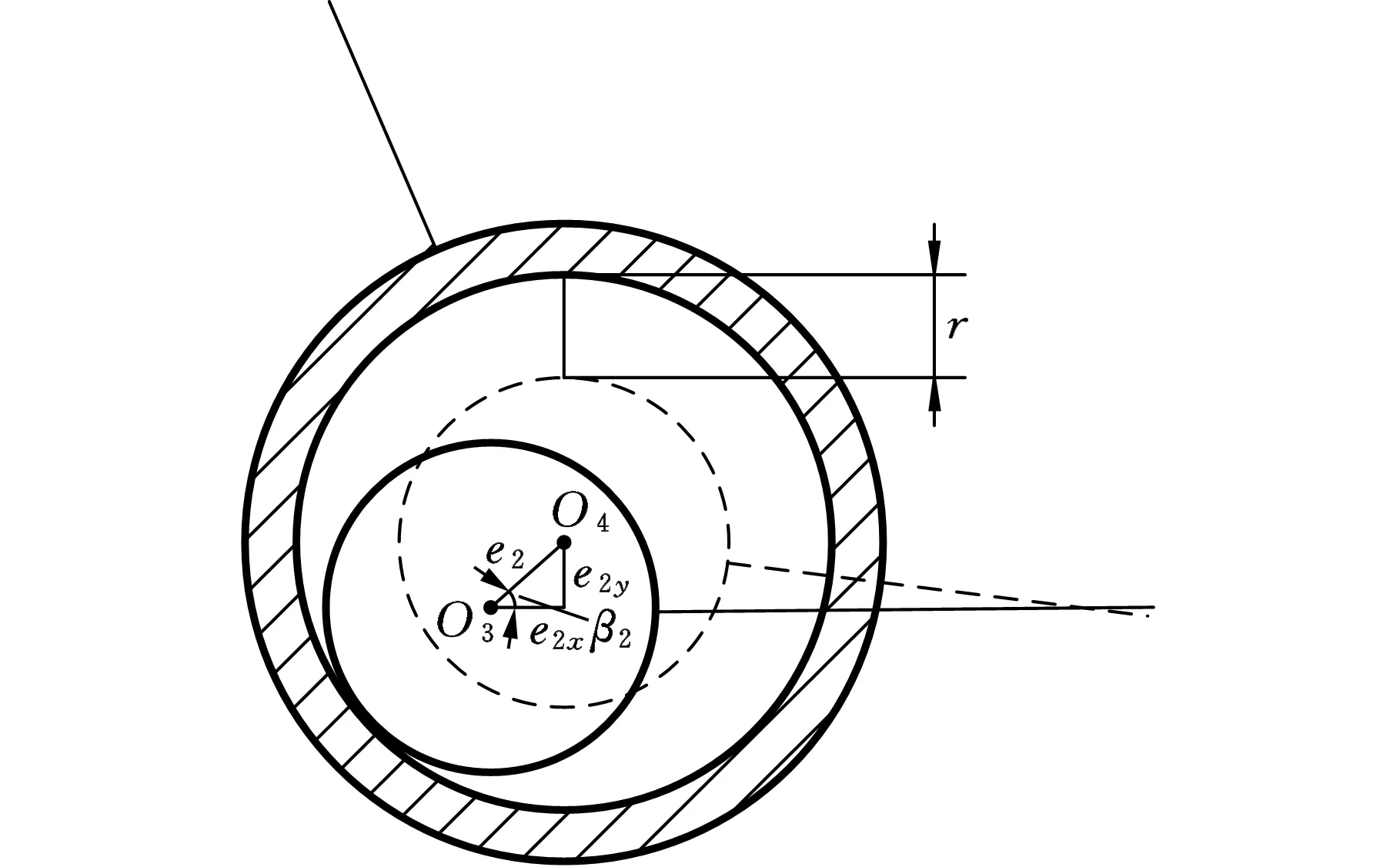
图3 运动副间隙放大图Fig.3 Enlarged drawing of the joint with clearance

考虑运动副接触表面滑动，运动副切向力用库仑摩擦力模型表述为

(2)

式中，f为摩擦因数；ρ为阶跃函数，ρ=sgnvt；Ct为切向阻尼系数；v2t为左侧接触点的切向速度；v1t为右侧接触点的切向速度。

左右两侧接触力在x向和y向的分力分别为

(3)

(4)

式中，β1为O1O2和x轴的夹角；β2为O3O4和x轴的夹角。

基于上述分析，间隙运动副对左右两侧转向节的力矩推导可得

M1=l2(F2ycosΦ2-F2xsinΦ2)+

R1(F2ycosβ2-F2xsinβ2)+F2ye2x-F2xe2y

(5)

M2=l3(F1xcosΦ1-F1ysinΦ1)+

R1(F1xcosβ1-F1ysinβ1)

(6)

式中，R1为轴销半径；l2、l3分别为左右梯形臂长度；Φ2、Φ1分别为转向梯形左右底角。

1.2 轮胎力学模型描述

胎体的弹性特性对转向轮摆振有重要影响[1]。制动时，汽车会发生瞬态的轴荷转移，轮胎侧偏特性会因纵向滑移率的变化而变化。因此复合工况下轮胎动态特性的准确描述是进行制动摆振动力学建模分析的前提。本文采用PAC2002模型[8]对其进行描述。复合工况下的侧偏力表达式为

Fy=Dyκcos(Cyκarctan(Byκκs-

Eyκ(Byκκs-arctan(Byκκs))))+SVyκ

(7)

κs=κ+SHκsCyκ=rCy1

Byκ=rBy1cos(arctan(rBy2(α-rBy3)))

Cyκ=Fy0/cos(Cyκarctan(ByκSHκs-

Eyκ(ByκSHκs-arctan(ByκSHκs))))

Eyκ=rEy1+rEy2dFz

SHyκ=rHy1+rHy2dFz

SVyκ=DVyκsin[rVy5arctan(rVy6κ)]

DVyκ=μyFz(rVy1+rVy2dFz+

rVy3γ)cos(arctan(rVy4α))

式中，κ为纵向滑移率；γ为外倾角；Fz为垂向载荷；α为侧偏角。

纯工况侧向力Fy0为复合工况侧向力Fy的加权基准，其表达式如下：

Fy0=Dysin(Cyarctan(Byαy-Ey(Byαy-

arctan(Byαy))))+SVy

(8)

αy=α+SHyCy=pCy1λCyDy=μyFzζ2

Ey=(pEy1+pEy2dFz)(1-(pEy3+pEy4γy)sgnαy)γEy

By=Ky/(CyDy)

SHy=(pHy1+pHy2dFz)λHy+pHy3γyζ0+ζ4-1

SVy=Fzλμyζ4((pVy1+pVy2dFz)λVy+

(pVy3+pVy4dFz)γy)

式(7)、式(8)中，pCy1、pDy1、pDy2、pDy3、pEy1、pEy2、pEy3、pEy4、pKy1、pKy2、pKy3、pHy1、pHy2、pHy3、pVy1、pVy2、pVy3、pVy4、rBy1、rBy2、rBy3、rCy1、rEy1、rEy2、rHy1、rHy2、rVy1、rVy2、rVy3、rVy4、rVy5、rVy6为待辨识的32个参数。本文根据样车轮胎六分力试验数据，通过设计Nelder-Mead法与随机值法相结合的参数辨识算法对公式进行数据拟合，得到上述32个参数。基于上述分析，复合工况侧向力Fy为α、κ、Fz、γ的函数，因此左右轮胎侧向力为

(9)

1.3 汽车ABS数学模型描述

汽车ABS数学模型描述如下

(10)

(11)

Fx=Fx0Gxα(α,κ,Fz)=Fx0·

(12)

式中，mi为1/4整车质量；I为车轮绕其转动轴的转动惯量；R为轮胎滚动半径；v为车速；ωr为车轮角速度；Tb为制动器制动力矩；Fx为复合工况纵向力；Fx0为纯工况纵向力；Bxα为刚度因子；Cxα为形状因子；Exα为曲率因子；αs为复合工况侧偏角；SHxs为复合工况水平漂移值。

纵向滑移可表示为

κ=(v-ωrR)/v

(13)

其最佳滑移率采用PID算法[11]进行控制。垂向轴荷更新为

Fz=G(b+zhg)/Lz

(14)

式中，G为汽车重力；b为后轴到质心的距离；z为制动强度；hg为汽车质心高度；Lz为前后轴轴距。

对比式(9)、式(13)与式(14)可见，制动造成的纵向滑移与轴荷转移会影响轮胎侧向受力。

1.4 摆振数学模型

根据第二类拉格朗日方程，并结合所建的子系统模型，可以推得汽车摆振数学模型。

系统的动能

(15)

式中，It为前轮绕主销的转动惯量；If为前桥侧摆绕其纵轴线的转动惯量；Iz为汽车横摆转动惯量；Is为横拉杆绕质心的转动惯量；m1为横拉杆质量。

系统的势能

Ep=(kw(Lθ1αr+ψB/2)2+

(16)

式中，kw为轮胎的垂直刚度；L为主销延长线与地面交点至车轮平面的距离；αr为主销后倾角;B为前轮距;kv为换算到绕主销的转向机构角刚度。

系统的耗散能

(17)

式中，ct为车轮绕主销转动的当量阻尼系数；cv为换算到绕主销转向机构的当量阻尼系数。

对应于系统的7个自由度，系统受到的广义力分别为

T1(Rα+ln)+M1

T2(Rα+ln)+M2

Q4=l1((F1x+F2x)sinΦ-(F1y+F2y)cosΦ)/2+

F1xe1y+R1(F1xsinβ1+F2xsinβ2-F1ycosβ1-

F2ycosβ2)-F1ye1x

Q5=F1x-F2xQ6=F1y-F2y

Q7=aFyf-bFyr

式中，mt为车轮质量；Ix为前轮绕与其转轴垂直的质心主轴的转动惯量；T1、T2分别为左右轮侧向力；M1、M2分别为间隙运动副接触力对左侧和右侧转向节的力矩；ln为轮胎拖矩；l1为横拉杆长度；a为前轴到质心的距离；Fyf、Fyr分别为前后轮胎受到地面的侧向力。

将上述能量与广义力代入第二类拉格朗日方程，得到系统微分方程：

T1(Rα+ln)-M1=0

kwLαB/2(θ1+θ2)+(T1+T2)R=0

F1xe1y-R1(F1xsinβ1+F2xsinβ2-F1ycosβ1-

F2ycosβ2)+F1ye1x=0

2 数值算例及结果讨论

基于上述所建分析模型，利用MATLAB数值算例对制动过程中摆振系统的动态响应进行分析，考察制动过程中摆振系统的动力学行为特征。本文推导的微分方程为含时变参数的刚性方程，具有很强的非线性。计算迭代时，考虑ABS制动过程，计入车速、纵向滑移率、垂向载荷等时变参数之间的数据传递，采用基于二阶Rosenbrock算法的改进算法对系统方程进行求解。

图4所示为摆振系统动态响应的一个算例。假设左前轮受到0.01 rad的初始激励，仿真初始车速v0=60 km/h，运动副间隙r=0.1 mm。可见转向轮摆振的同时伴随一定的横摆，整个制动过程中，摆振响应先增大后减小，最后逐渐衰减至零。汽车横摆与转向轮摆振响应有相似的变化规律。

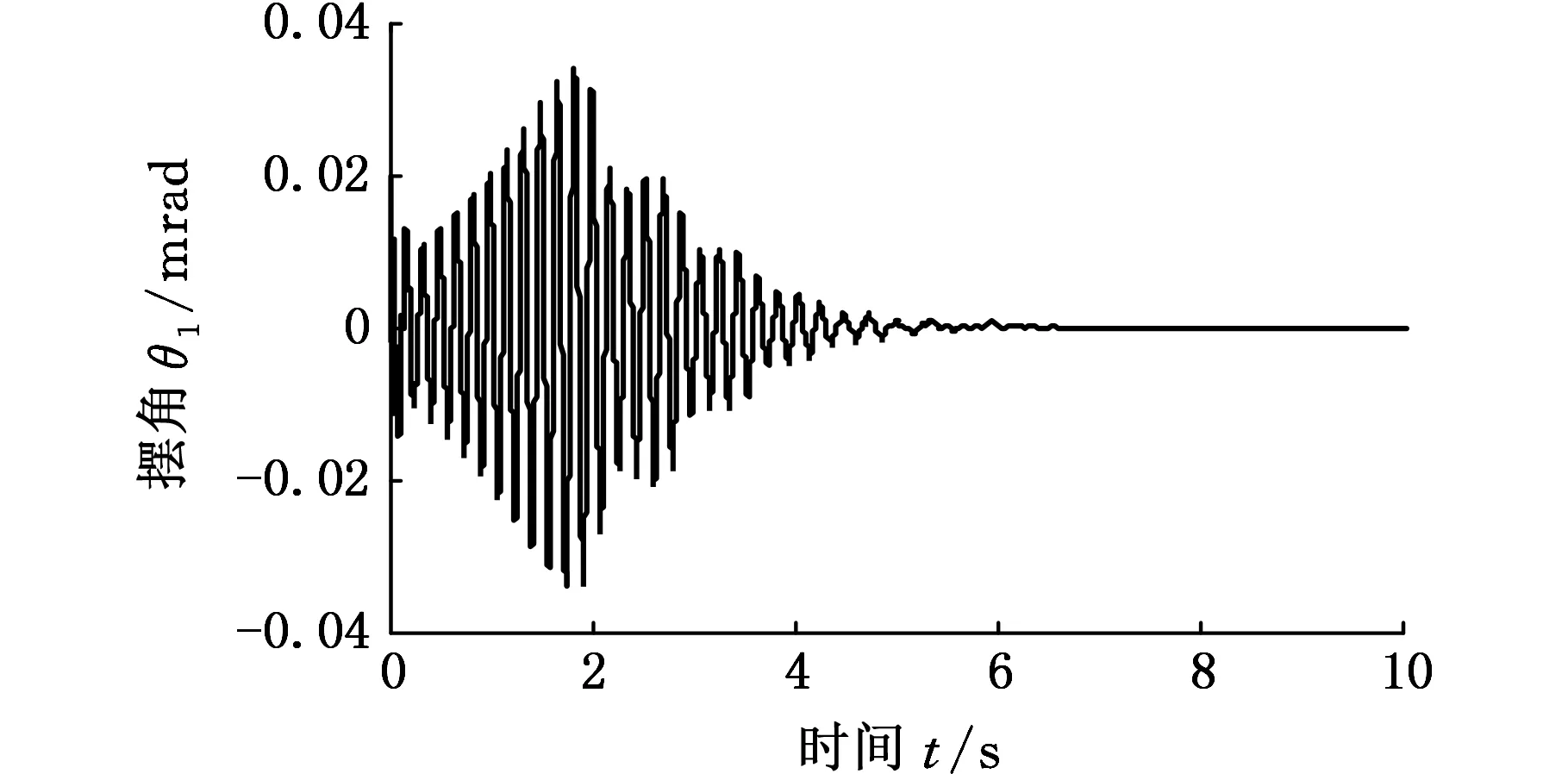
(a)左轮摆角时间历程

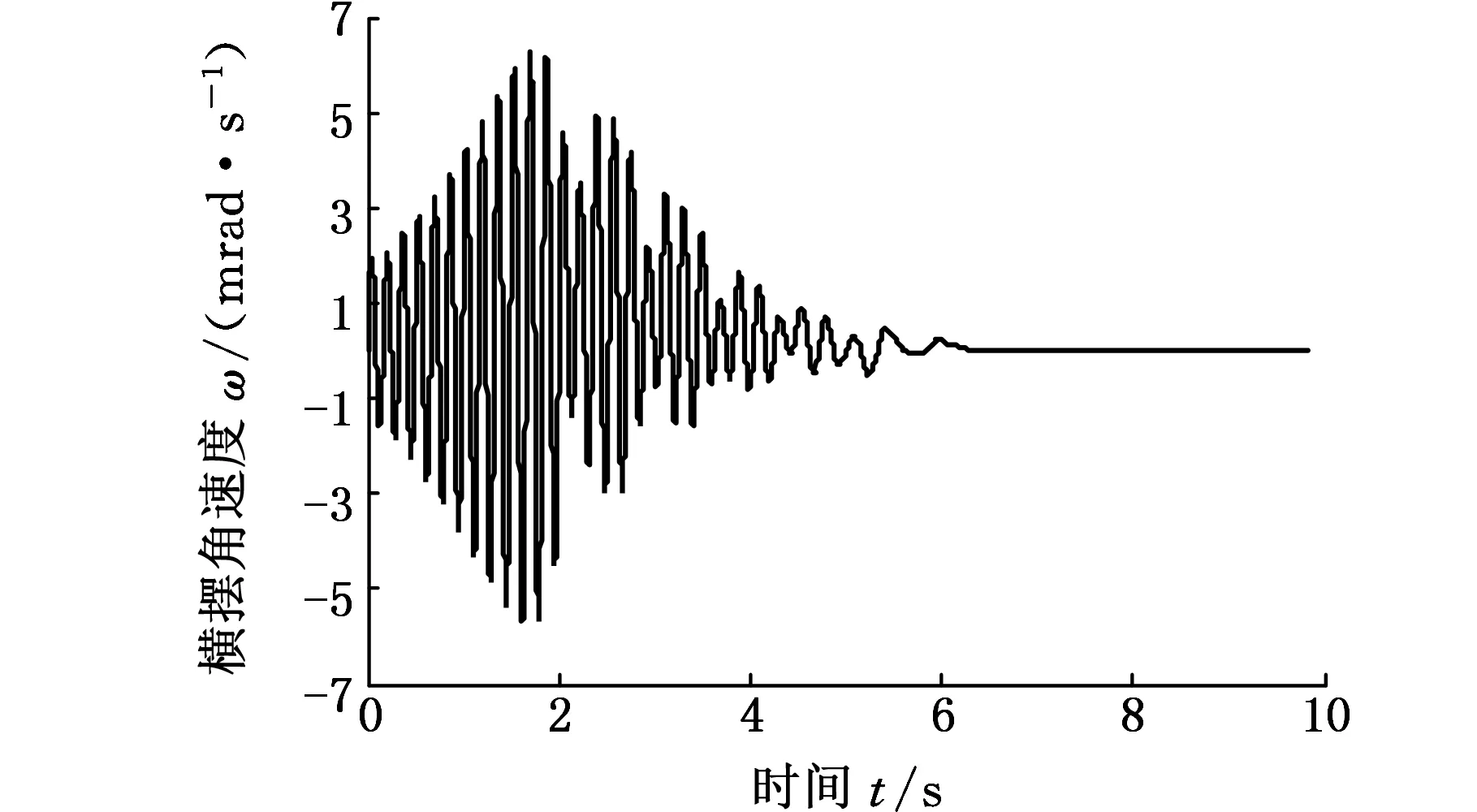
(b)横摆角速度时间历程图4 考虑轴荷转移的摆振动态响应(v0=60 km/h)Fig.4 Dynamic response of vehicle shimmy with consideration of load transfer(v0=60 km/h)

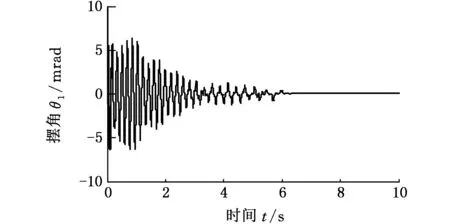
(a)左轮摆角时间历程

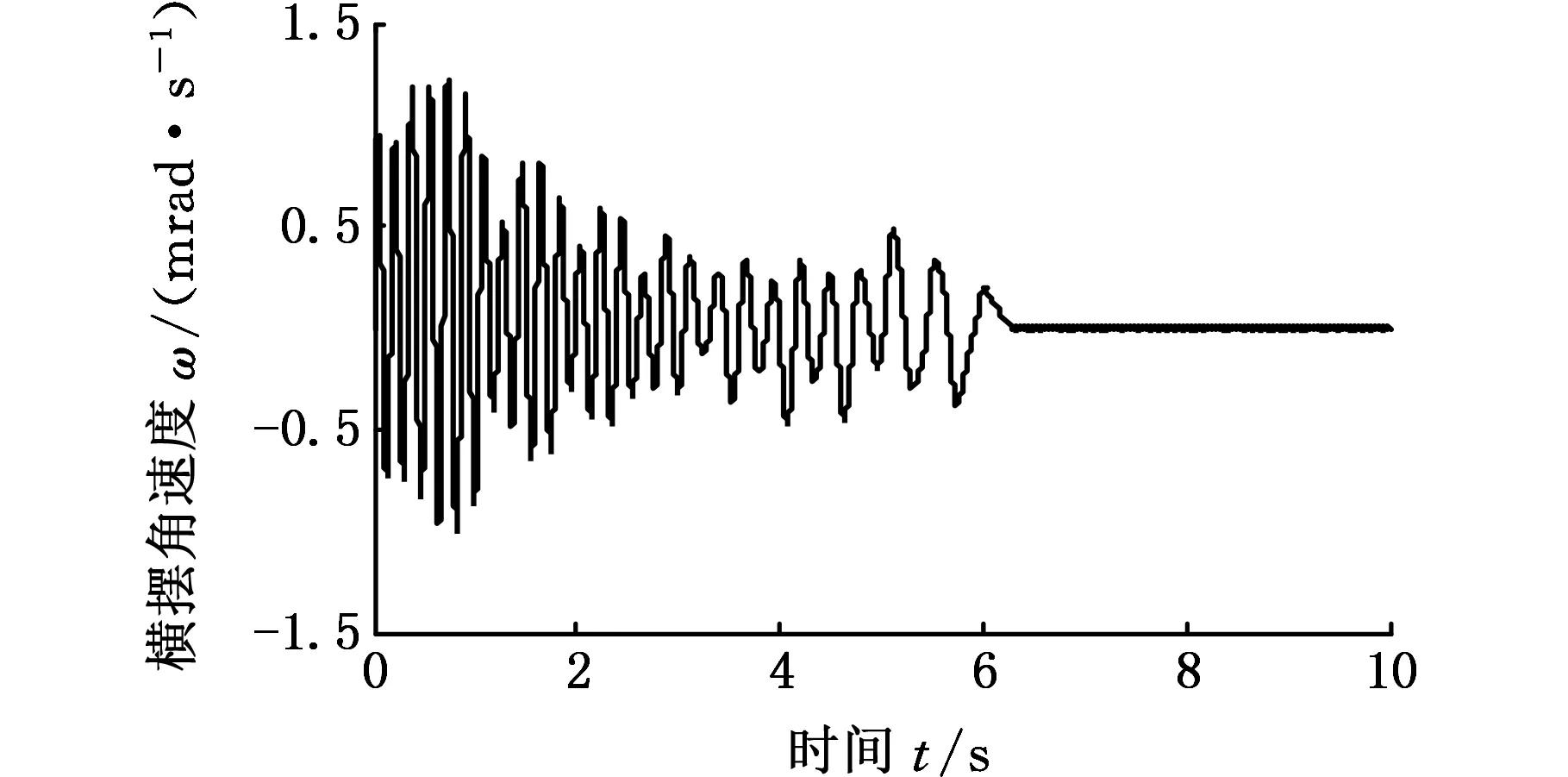
(b)横摆角速度时间历程图5 忽略轴荷转移的摆振动态响应(v0=60 km/h)Fig.5 Dynamic response of vehicle shimmy without consideration of load transfer(v0=60 km/h)

另外,对相同车型参数下，忽略制动过程中轴荷转移的摆振动态响应进行仿真，如图5所示。对比图4可以发现,转向轮摆角与汽车横摆响应均大幅减小,因此制动过程中的轴荷转移会加剧摆振。

改变初始车速发现,系统的动态响应峰值与响应时间都有较大的变化。对比图4、图6与图7可见，初始车速越大，摆振瞬态响应时间越长。

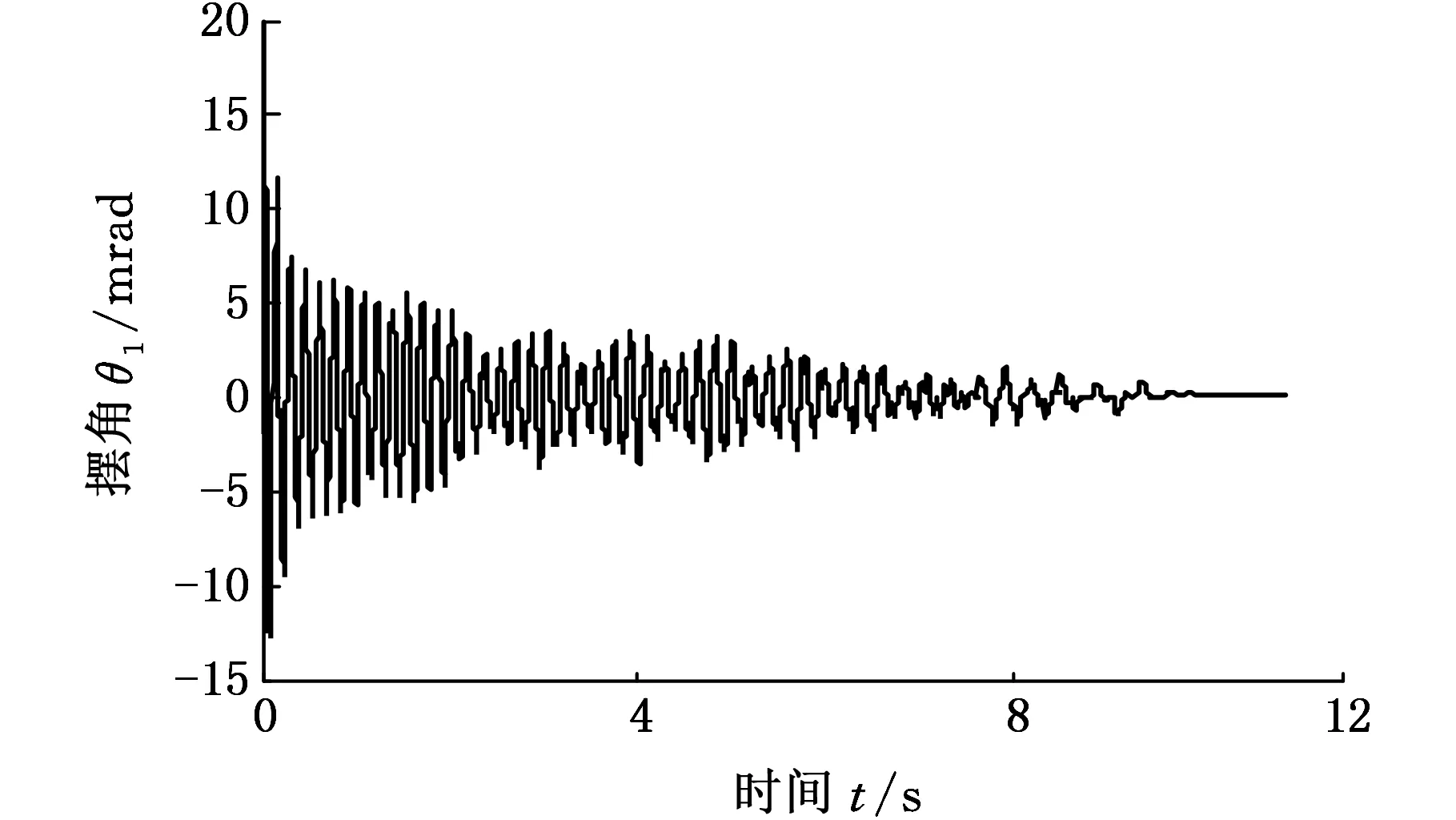
图6 左轮摆角时间历程(v0=100 km/h)Fig.6 Time history of left wheel(v0=100 km/h)

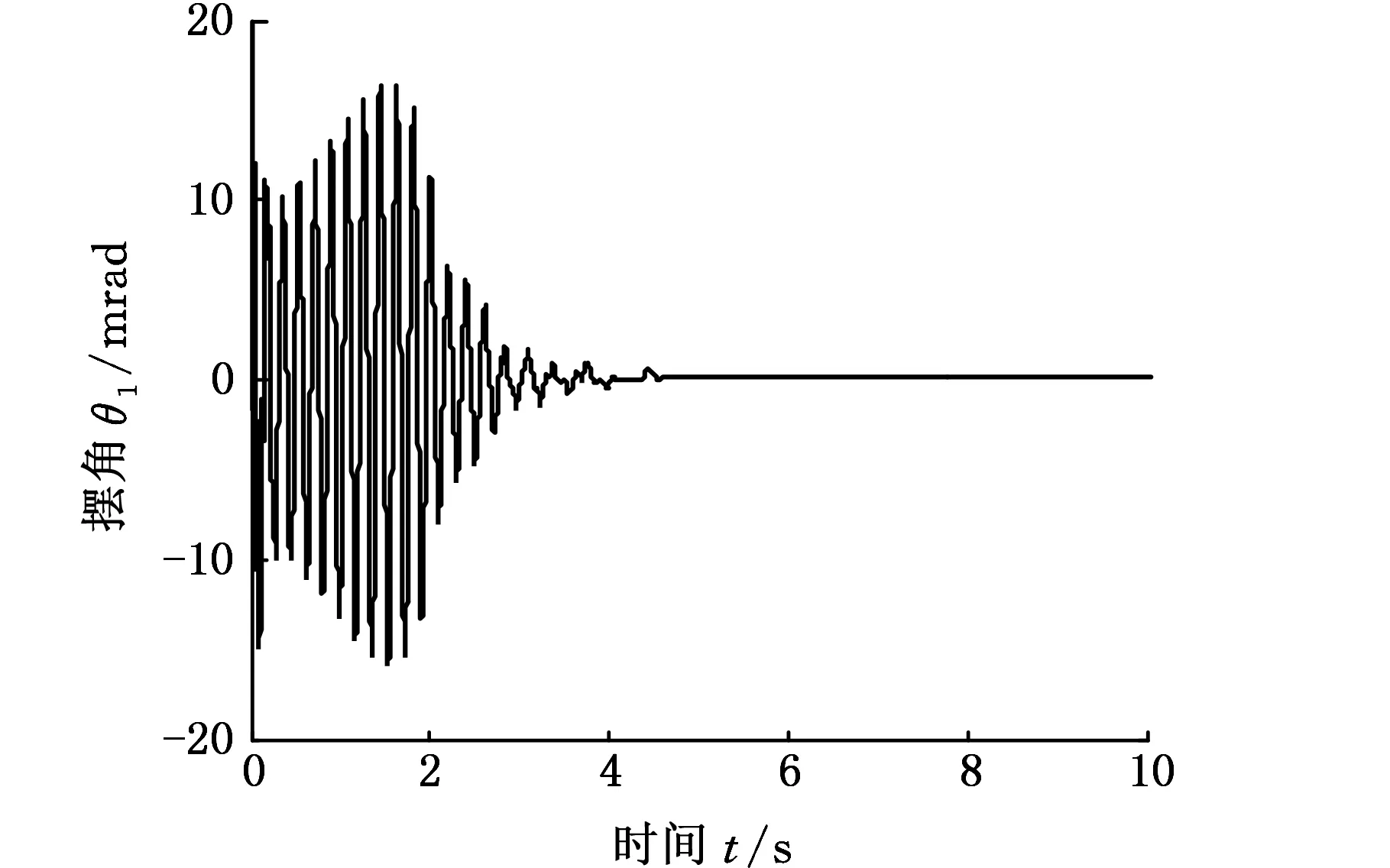
图7 左轮摆角时间历程(v0=40 km/h)Fig.7 Time history of left wheel(v0=40 km/h)

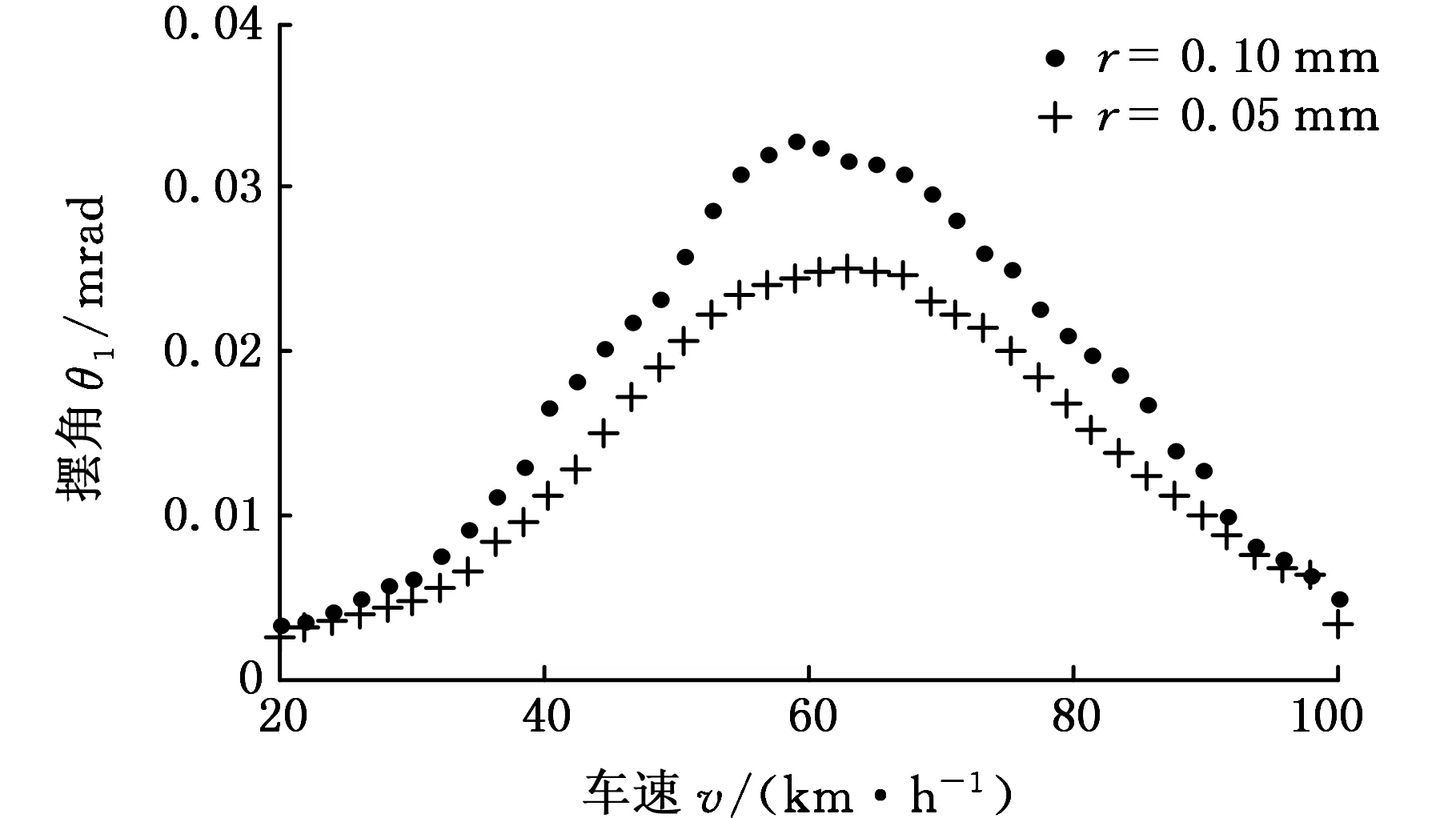
图8 左轮摆角最大值随初始车速变化曲线Fig.8 Diagram for the response amplitude of left wheel with different vehicle speed

图8所示为间隙r为0.1 mm、0.05 mm两种情况下左轮摆角最大值随初始车速的变化曲线，可以看出，在整个车速范围内，车辆都会发生摆振现象，摆角幅值随车速先增大后减小。车速在40～80 km/h范围内的振动相对剧烈，与图9所示的试车情况基本吻合，这在一定程度上验证了模型的正确性。另外，对比不同间隙大小时的系统响应可以看出，间隙较大时，摆振振幅也较大。

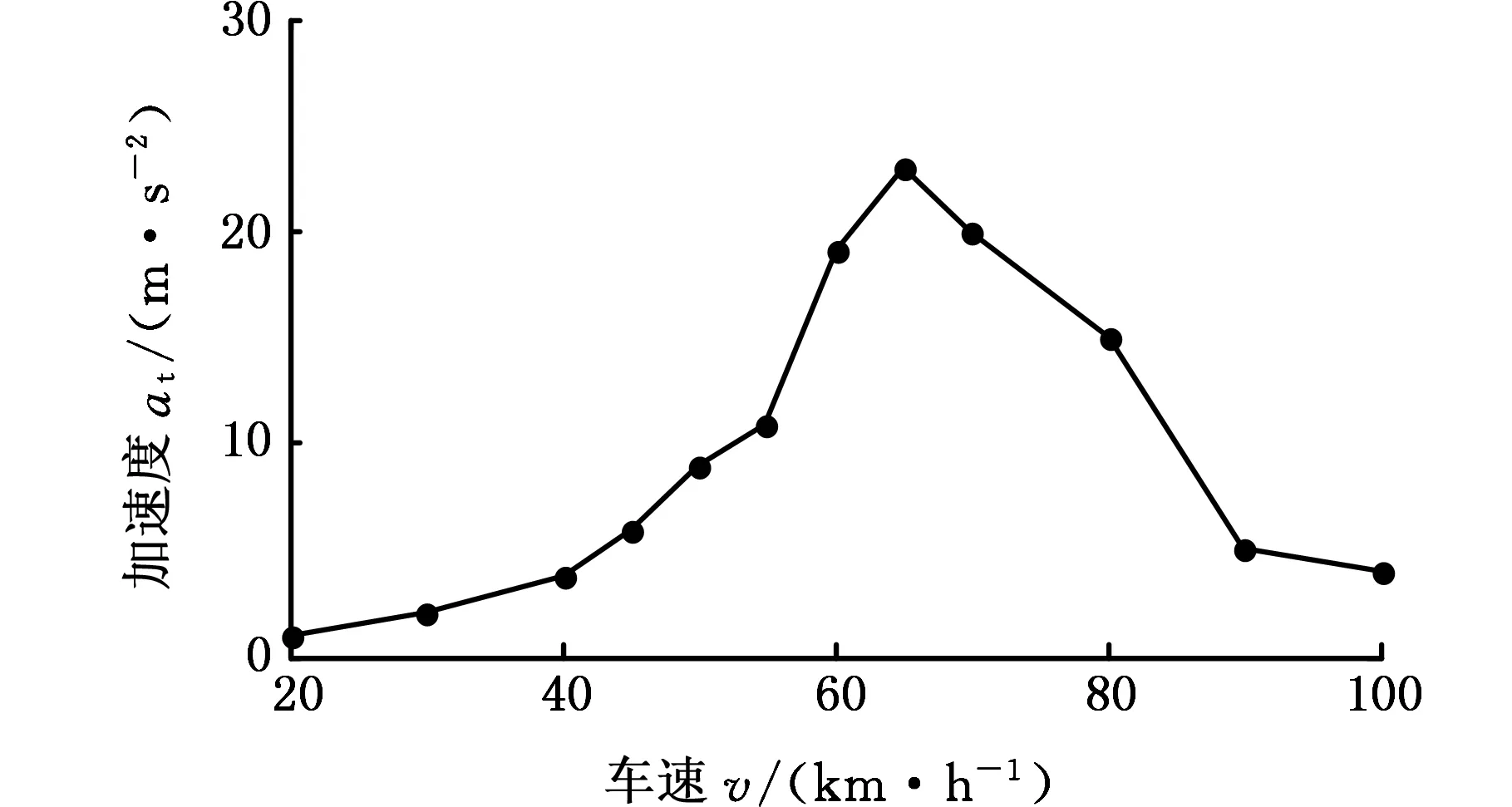
图9 摆振试验结果曲线Fig.9 Diagram for the shimmy experimental data

制动过程中，减小摆振的瞬态响应时间有利于提高汽车操纵稳定性。通过仿真分析，从理论上考察系统各参数对瞬态响应时间的影响。以图4所示工况为基准，图10所示为减小前轴中心线至汽车质心距离时的摆振时间历程。通过对比看出，减小前轴距可以缩短摆振的瞬态响应时间，这对抑制摆振是有利的。

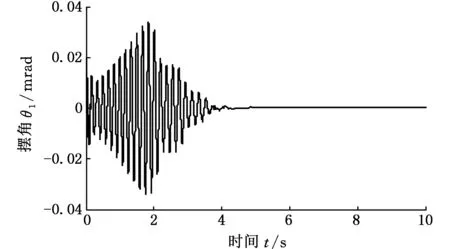
图10 左轮摆角时间历程Fig.10 Time history of left wheel

3 结论

(1)转向轮摆振的同时伴随一定的横摆，整个制动过程中，摆振响应先增大后减小，最后逐渐衰减至零。制动过程中的轴荷转移会加剧摆振。

(2)初始车速对系统的瞬态响应时间与响应峰值都有较大的影响。初始车速越大，摆振瞬态响应时间越长。摆振瞬态响应峰值随车速先增大后减小，中等车速范围内的振动程度相对剧烈，与试验结果基本吻合，这在一定程度上验证了模型的正确性。

(3)间隙的增大会加剧摆振。减小前轴中心线至汽车质心的距离可以缩短摆振的瞬态响应时间，这有利于抑制摆振，提高汽车操纵稳定性。

[1] PACEJKA H B. Tyre and Vehicle Dynamics[M]. 2nd ed. Oxford:Butterworth and Heinemann, 2006.

[2] METRIKIN V S, PEISEL M A. Calculation of Flight Vehicle Main Support Wheel Vibrations Taking into Account Brake Forces[J]. Russian Aeronautics (Iz.VUZ), 2012, 55(2):144-150.

[3] 张立军, 宁国宝, 尹东晓, 等. 制动力矩波动引起方向盘抖动的传递途径试验研究[J]. 振动与冲击, 2006, 25(2):70-74. ZHANG Lijun, NING Guobao, YIN Dongxiao, et al. Experimental Research on the Transfer Path of Steering Wheel Wobbling Induced by Brake Judder[J]. Journal of Vibration and Shock, 2006, 25(2):70-74.

[4] KRÜGER W R, MORANDINI M. Recent Developments at the Numerical Simulation of Landing Gear Dynamics[J]. CEAS Aeronautical Journal, 2011,1(1/4):55-68.

[5] LI S, LIN Y. Study on the Bifurcation Character of Steering Wheel Self-excited Shimmy of Motor Vehicle[J]. Vehicle System Dynamics, 2006, 44(S1):115-128.

[6] KOVACS A P. Computational Vibration Analysis of Vehicle Shimmy by a Power-work Method[J]. Vehicle System Dynamics, 1998, 29(6):341-364.

[7] 刘喜东, 马建, 郭荣庆. 制动工况下汽车转向系统敏感度分析方法[J]. 交通运输工程学报, 2008, 8(3):20-23. LIU Xidong, MA Jian, GUO Rongqing. Sensitivity Analysis Method of Vehicle Steering System under Braking Condition [J]. Journal of Traffic and Transportation Engineering, 2008, 8(3):20-23.

[8] LU Jianwei, XIN Jiayun, VAKAKIS A F, et al. Influences of System Parameters on Dynamic Behavior of the Vehicle Shimmy System with Clearance in Steering Linkage[J]. Journal of Vibration and Control, 2015, 21(2):359-370.

[9] 卢剑伟, 吴彰伟, 吴继祥, 等. 考虑齿轮-齿条转向器侧隙的汽车摆振系统动力学建模及分析[J]. 中国机械工程, 2012, 23(22):2765-2768. LU Jianwei, WU Zhangwei, WU Jixiang, et al. Dynamic Modeling and Analysis of Vehicle Shimmy System with Consideration of Rack-and-pinion Steering Box Backlash[J]. China Mechanical Engineering, 2012, 23(22):2765-2768.

[10] THOTA P, KRAUSKOP B, LOWENBERG M. Multi-parameter Bifurcation Study of Shimmy Oscillations in a Dual-wheel Aircraft Nose Landing Gear[J]. Nonlinear Dynamics, 2012, 70(2):1675-1688.

[11] 李以农, 郑玲, 谯艳娟. 汽车纵向动力学系统的模糊PID控制[J]. 中国机械工程, 2006, 17(1):99-103. LI Yinong, ZHENG Ling, QIAO Yanjuan. Fuzzy-PID Control Method on Vehicle Longitudinal Dynamics System[J]. China Mechanical Engineering, 2006, 17(1):99-103.

(编辑 张 洋)

Dynamic Response of Shimmy Systems under Braking Conditions with Consideration of Clearances in Joints

JIANG Junzhao1LU Jianwei1LI Jinhui1YANG Shiqin2

1. School of Automotive and Transportation Engineering,Hefei University of Technology,Hefei,2300092.Research Center of Passenger Car,Jianghuai Automobile Co.,Ltd.,Hefei,230601

A 7-DOF dynamic model under braking conditions was established, where time-varying characteristics of parameters and dynamic coupling among movement pairs with clearances were taken into account. Dynamic response analysis of shimmy system under braking conditions was carried out through numerical examples with MATLAB. Moreover, influences of load transfers, vehicle speeds, clearances and wheelbases on transient response of shimmy system were discussed. It is concluded that the time-varying characteristics of parameters under braking conditions and dynamic coupling in joints with clearances may have great influences on dynamic behaviors of shimmy, which should be taken into account in system modeling. The conclusions agree with the experimental results in general, which may verify the accuracy of the dynamic model.

shimmy; braking; clearance; load transfer; transient response

2016-09-20

国家自然科学基金资助项目(50975071)；教育部新世纪优秀人才支持计划资助项目(NCET-10-0358)；安徽省高校省级自然科学研究重大项目(KJ2014ZD06)

U461.61;TH132

10.3969/j.issn.1004-132X.2017.14.004

姜俊昭，男，1987年生。合肥工业大学汽车与交通工程学院博士研究生。主要研究方向为汽车系统动力学。发表论文3篇。E-mail:chlgch.2006@163.com。卢剑伟，男，1975年生。合肥工业大学汽车与交通工程学院教授、博士研究生导师。李金辉，男，1991年生。合肥工业大学汽车与交通工程学院硕士研究生。杨士钦，男，1973年生。江淮汽车股份有限公司乘用车研究院院长。