盾构隧道EPDM橡胶密封垫本构参数试验研究
秦正贵
(1. 河海大学土木与交通学院, 江苏 南京 210098; 2. 中铁第六勘察设计院集团有限公司, 天津 300308)
盾构隧道EPDM橡胶密封垫本构参数试验研究
秦正贵1, 2
(1. 河海大学土木与交通学院, 江苏 南京 210098; 2. 中铁第六勘察设计院集团有限公司, 天津 300308)
为合理确定盾构隧道接缝EPDM弹性密封垫橡胶材料的本构模型及其参数,采用CMT4304型微机控制电子万能试验机,进行单轴拉伸试验和单轴压缩试验,并利用ABAQUS有限元分析软件对试验数据进行分析,从模型符合性和材料稳定性2方面进行评价,得出常用硬度EPDM橡胶材料的推荐本构模型及其参数。结果表明: 邵尔硬度为45 HA和60 HA的EPDM橡胶,采用Arruda-Boyce 或van der Waals本构模型较合适; 邵尔硬度为55 HA的EPDM橡胶,采用Arruda-Boyce 或Yeoh本构模型较合适; 邵尔硬度为65 HA的EPDM橡胶,采用Mooeny-Rivlin本构模型较合适。
盾构隧道; EPDM橡胶; 防水; 本构模型; 邵尔硬度
0 引言
近年来,我国城市轨道交通和水下隧道建设得到了快速发展,并取得了显著的成就。其施工工法中,盾构法占有主导地位。管片接缝防水是盾构法隧道的一项重要研究内容。采用EPDM橡胶材料制作弹性密封垫用来防水,是目前盾构隧道防水的主流方法,但在高烈度区修建隧道时,对防水设计提出了更高要求。为节省成本和提高效率,目前的弹性密封垫设计,一般先采用有限元方法进行仿真分析优化,然后进行试验验证。要得到正确、合理的有限元分析结论,必须先对EPDM橡胶材料的本构模型及其参数进行研究。
橡胶材料具有超弹性、非线性和近乎不可压缩的性质,一般采用应变能密度函数来描述其本构关系。基于统计热力学,把橡胶看成是许多不规则长链分子的组合体。Treloar将高斯统计学应用于高分子网链中来描述橡胶材料的宏观行为,得出一个基于统计学的描述橡胶变形的应变能密度函数式[1]。这种统计模型不能描述分子链的全部伸展过程,只能近似预测小变形的情况。为克服此种局限,后来的研究基本采用非高斯统计学理论。其中Arruda和Boyce提出一种八链分子网络模型,得出一个与试验数据符合更好的应变能密度函数式[2]。而另一种思路是基于连续介质力学,把橡胶看成是一种各向同性的不可压缩弹性体。Mooney最早得出一个应变能函数式[3],后来被广泛采用。Rivlin推导出一个更一般的偶次幂的多项式应变能密度函数[4-5],而Mooney的成果只是它的一种简单特例。Yeoh通过试验研究建议应变能密度函数不包含第二应变不变量,并提出一个三次应变能密度函数式,能够描述剪切模量的变化[6]。Gent从唯象法出发提出一个考虑了分子链极限伸长率影响的新模型[7],之后Boyce把Gent的新模型应变能密度函数式中自然对数项展开,得到一个只包含第一应变不变量的缩减多项式[8],它是Yeoh应变能密度函数式的扩展。此外,与分子链极限伸长率有关的具有较大影响的模型还有Kilian建立的van der Waals模型[9-10]。前述模型的应变能函数式均是应变不变量的函数,而Ogden认为这样做是将问题复杂化,他提出一个直接采用伸长率作为自变量的应变能函数式[11],后来应用较广。国内也有学者对前述模型进行了改进研究[12],但目前尚未得到普遍关注。
综上可知,已有对橡胶材料本构模型的研究较多,并取得了一些成果,但目前还没有得到一个对各种试验数据均较为符合的理想模型。针对盾构防水常用的EPDM橡胶材料,尚未见关于本构模型及对应参数选取方法的研究报道。本文通过单轴压缩和单轴拉伸试验,旨在合理确定盾构防水中几种常用硬度的EPDM橡胶材料的本构模型及其参数,以便为弹性密封垫设计中有限元分析提供可靠的材料参数基础资料。
1 本构模型
1.1 基于热力学统计的本构模型
该领域应用较广的本构模型有Arruda-Boyce模型[2],其应变能函数式为

(1)

1.2 基于连续介质的现象学的本构模型
该领域应用较广的本构模型较多,其应变能函数式如下。
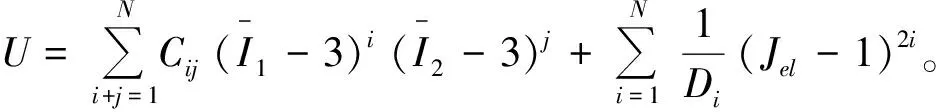
其中

(3)
3)Mooney-Rivlin模型[3]。式(2)中N取1时,有
(4)
4)Yeoh模型[6]。式(3)取前3项时,有
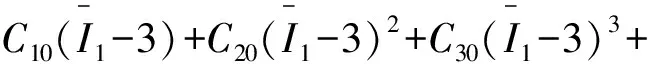
(5)
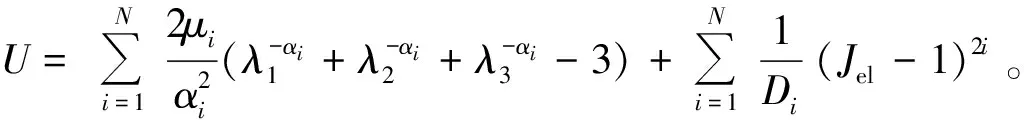
(6)
式中μi、αi、Di均为待定材料参数。
6)van der Waals模型[9-10]。
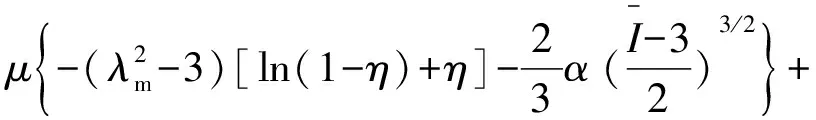
(7)
其中
式中μ、λm、α、β、D为待定材料系数。
1.3 应力-应变关系
橡胶材料应力-应变关系为: 假设材料完全不可压缩(弹性体变率Jel=1),则

(8)
式中:σij为应力张量;εij为应变张量。
2 试验
橡胶材料试验可分为单轴试验、双轴试验、平面试验和三轴试验。上述每类试验又可分为拉伸和压缩2种。本次试验采用CMT4304型微机控制电子万能试验机,对盾构防水中常用的几种硬度EPDM材料进行多样品的单轴拉伸和单轴压缩试验,见表1和图1。单轴拉伸试验按照文献[13]中1型试样的要求实施,单轴压缩试验按照文献[14]中A法的要求实施,为消除摩擦对橡胶横向变形的约束作用,样品两端均涂抹了润滑剂。
图2—9示出不同硬度橡胶单轴拉伸试验和单轴压缩试验结果。可以看出: 同类试验同一硬度的3个样品具有良好的一致性;随着橡胶硬度增大,产生同样大小的名义应变,所需的力越大。
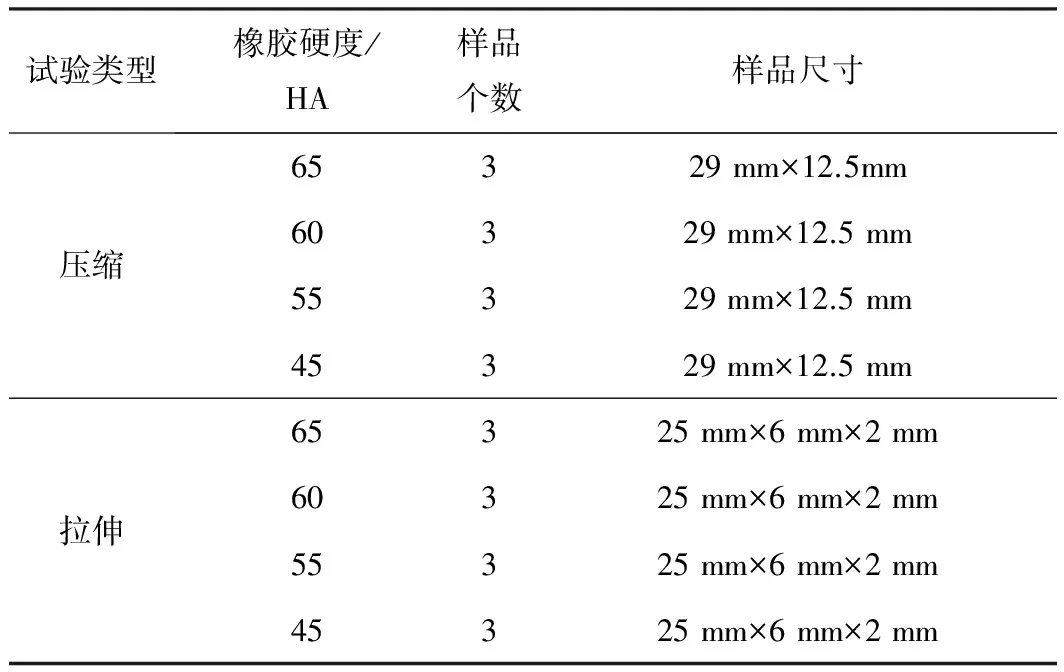
表1 试验样品统计表

图1 试验样品Fig. 1 Experimental samples

图2 邵尔硬度为45 HA的EPDM橡胶单轴拉伸试验
Fig. 2 Uniaxial tensile test on EPDM rubber with Shore hardness of 45 HA
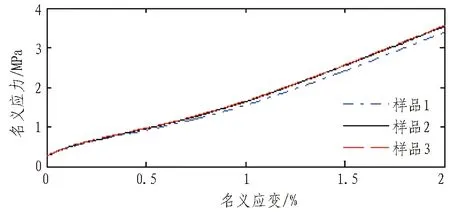
图3 邵尔硬度为55 HA的EPDM橡胶单轴拉伸试验
Fig. 3 Uniaxial tensile test on EPDM rubber with Shore hardness of 55 HA

图4 邵尔硬度为60 HA的EPDM橡胶单轴拉伸试验
Fig. 4 Uniaxial tensile test on EPDM rubber with Shore hardness of 60 HA
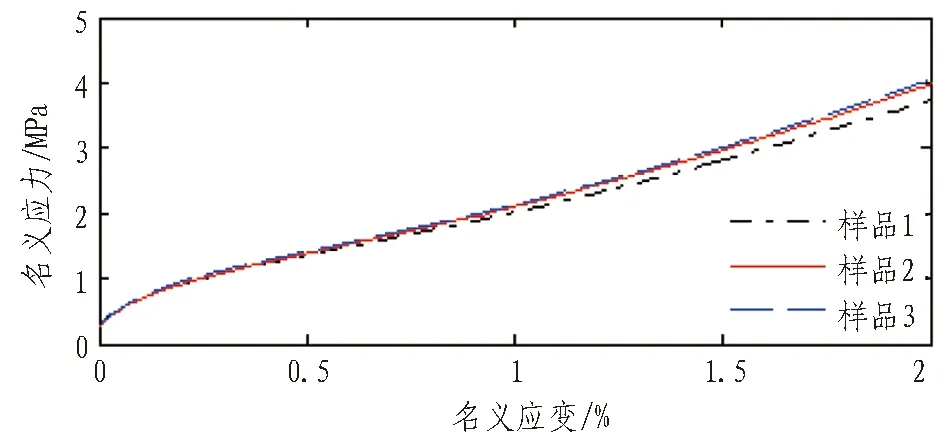
图5 邵尔硬度为65 HA的EPDM橡胶单轴拉伸试验
Fig. 5 Uniaxial tensile test on EPDM rubber with Shore hardness of 65 HA

图6 邵尔硬度为45 HA的EPDM橡胶单轴压缩试验
Fig. 6 Uniaxial compression test on EPDM rubber with Shore hardness of 45 HA

图7 邵尔硬度为55 HA的EPDM橡胶单轴压缩试验
Fig. 7 Uniaxial compression test on EPDM rubber with Shore hardness of 55 HA
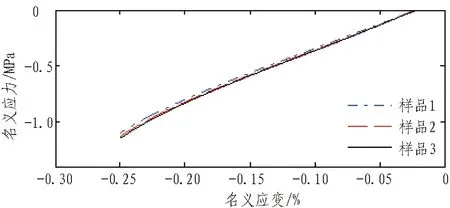
图8 邵尔硬度为60 HA的EPDM橡胶单轴压缩试验
Fig. 8 Uniaxial compression test on EPDM rubber with Shore hardness of 60 HA
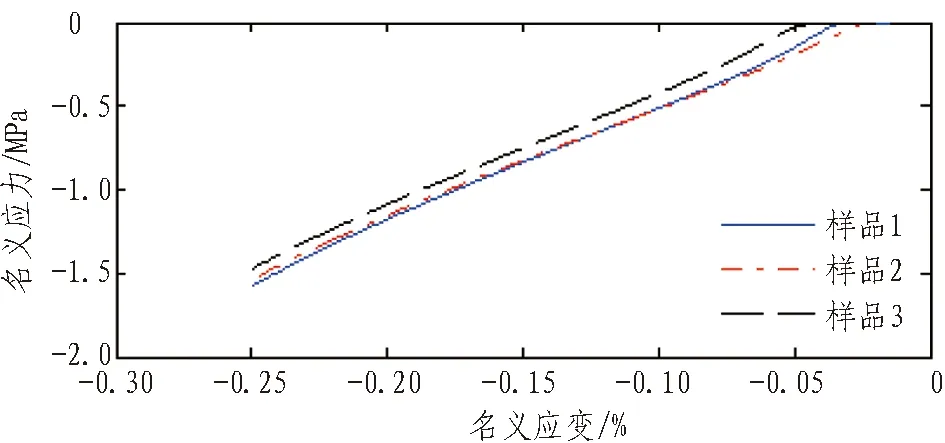
图9 邵尔硬度为65 HA的EPDM橡胶单轴压缩试验
Fig. 9 Uniaxial compression test on EPDM rubber with Shore hardness of 65 HA
3 数据分析
有限元软件ABAQUS具备分析材料试验数据并确定其本构参数的功能,具体分为2项内容: 1)通过数据拟合,确定本构参数; 2)评价这些参数确定的本构模型材料的稳定性。
3.1 数据拟合
试验数据中,每个名义应变会单独对应1个名义应力,这样1对数据代入式(8)就得到1个方程,如有n对数据,就得到1个由n个方程组成的方程组,当n大于方程组中的未知待定材料参数时,利用最小二乘法确定模型的最佳参数[13]。
图10—13为不同硬度橡胶的试验数据与本构模型的拟合图,其符合程度分级统计见表2。试验结果显示: 对邵尔硬度为65 HA的EPDM橡胶,只有Mooney-Rivlin模型能够较好地模拟;对其他硬度材料,Yeoh、Arruda-Boyce和van der Waals模型均能较好地模拟。Ogden 模型对所有材料均表现不佳。

图10 邵尔硬度为45 HA的EPDM橡胶试验数据拟合图
Fig. 10 Fitting chart of test data for EPDM rubber with Shore hardness of 45 HA

图11 邵尔硬度为55 HA的EPDM橡胶试验数据拟合图
Fig. 11 Fitting chart of test data for EPDM rubber with Shore hardness of 55 HA
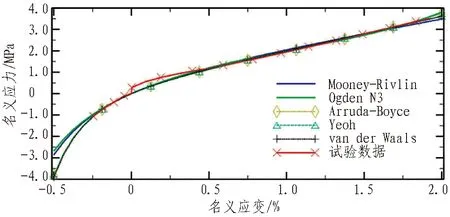
图12 邵尔硬度为60 HA的EPDM橡胶试验数据拟合图
Fig. 12 Fitting chart of test data for EPDM rubber with Shore hardness of 60 HA
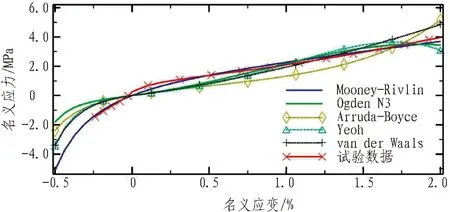
图13 邵尔硬度为65 HA的EPDM橡胶试验数据拟合图
Fig. 13 Fitting chart of test data for EPDM rubber with Shore hardness of 65 HA
表2 样品试验数据与本构模型符合程度统计表
Table 2 Statistics of coincidence degree of sample test data and constitutive model

橡胶硬度/HAMooney-RivlinOgdenN3YeohArruda-BoycevanderWaals45∗∗∗∗∗∗∗∗∗∗∗∗55∗∗∗∗∗∗∗∗∗∗∗∗60∗∗∗∗∗∗∗∗∗∗∗∗65∗∗∗∗∗∗∗
注: *表示本构模型与试验数据符合性差;**表示本构模型与试验数据符合性一般;***表示本构模型与试验数据符合性好。
3.2 材料稳定性
采用本构模型所描述的材料,必须满足材料稳定性(应力增加,应变随之增加)Drucker公设,即: dε为任意无穷小的对数应变,对应的应力为dσ,要求满足
dσ∶dε>0。
(9)
对于各向同性材料,也可写成
dσ1·dε1+dσ2·dε2+dσ3·dε3>0。
设dσ=D∶dε,则有
dεT∶D∶dε>0,
(10)
即要求刚度矩阵D是正定的。如材料不可压缩,则可假设任何静水压力值而不影响应变,最方便的做法是: 假设σ3=dσ3=0,有
(11)
要求刚度矩阵D是正定的,则有Dij=Dij(λ1,λ2,λ3)满足不等式组
(12)
在Abaqus中,将6种不同的荷载形式(单轴拉伸和压缩、双轴拉伸和压缩、平面拉伸和压缩)按不等式(12)检验材料稳定性,检验的伸长比范围为0.1<λ1<10,步长为Δλ1=0.01。
表3为材料稳定性统计表。从表可知,只有Arruda-Boyce模型对各种硬度的EPDM橡胶不具有稳定性限制,而对于其他各模型,一般均要求应变在一定范围内才能满足材料稳定要求。

表3 材料稳定性统计表Table 3 Statistics of stability of materials
注: √表示材料稳定性不受限制。
3.3 分析结论
在满足稳定性的条件下,选择与试验数据拟合最好的模型,针对不同硬度的EPDM橡胶,建议采用的模型及其非零参数统计见表4。
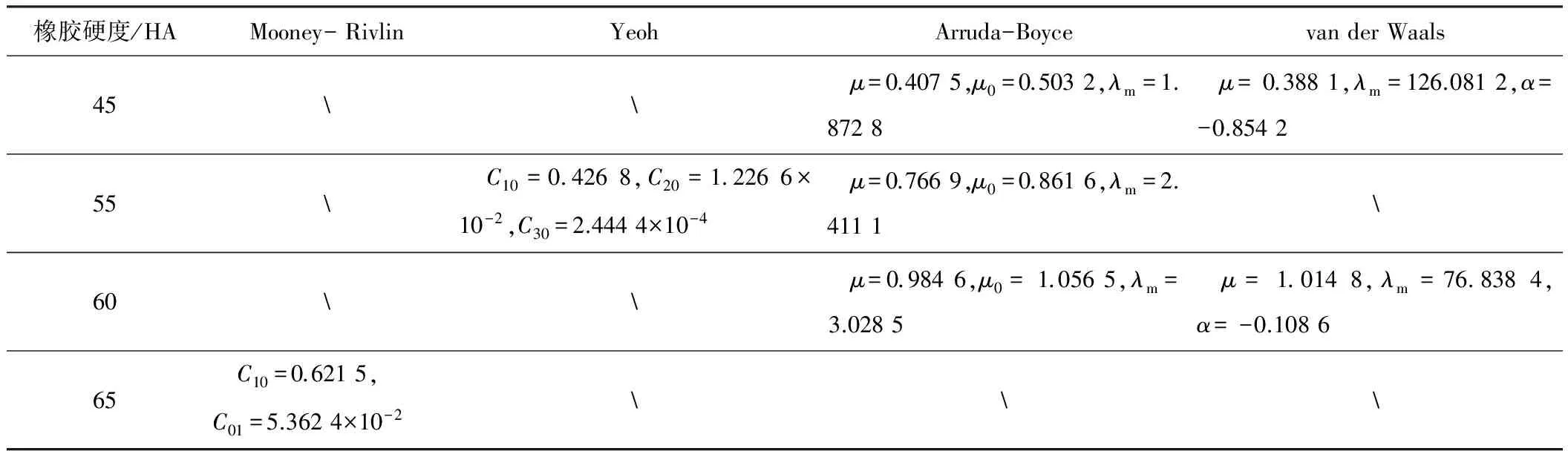
表4 建议模型及其非零参数统计表
注: 表示模型不适用。
4 结论和讨论
1)通过试验并采用ABAQUS有限元软件对试验数据进行分析,给出4种常用硬度的EPDM橡胶材料的推荐本构模型及其参数。对邵尔硬度为45 HA和60 HA的EPDM橡胶,建议采用Arruda-Boyce 或van der Waals本构模型;对邵尔硬度为55 HA的EPDM橡胶,建议采用Arruda-Boyce 或Yeoh本构模型;对邵尔硬度为65 HA的EPDM橡胶,建议采用Mooeny-Rivlin本构模型。
2)针对具体某项工程,设计盾构防水弹性密封垫,可先采用有限元进行仿真分析,初步确定其几何参数和材料,然后制样验证。进行有限元分析时,可采用本文推荐的材料本构模型及其参数。
3)本文提供了一种盾构接缝防水EPDM密封垫本构模型选取的解决方案及思路,可供类似工程开展防水设计借鉴和参考;但由于本文仅提供了4种常用硬度EPDM橡胶的本构模型的选取指导意见,后续尚需开展更多试验研究及论证,据以考虑更多硬度及其他影响因素。
[1] TRELOAR L R G. The elasticity of a network of long chain molecules (Ⅲ) [J]. Transactions of the Faraday Society, 1946, 42(4): 83-94.
[2] ARRUDA E M, BOYCE M C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials [J]. Journal of the Mechanics and Physics of Solids, 1993, 41(2): 389-412.
[3] MOONEY M. A theory of large elastic deformation [J]. Journal of Applied Physics, 1940, 11(9): 582-592.
[4] RIVLIN R S. Large elastic deformation of isotropic materials ( Ⅰ ): Fundamental concepts [J]. Philosophical Transactions of the Royal Society of London, 1948, 240(822): 459-490.
[5] RIVLIN R S. Large elastic deformation of isotropic materials (Ⅱ): Some uniqueness theories for pure, homogeneous deformations [J]. Philosophical Transactions of the Royal Society of London, 1948, 240(822): 491-508.
[6] YEOH O H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates [J]. Rubber Chemistry and Technology, 1990, 63(5): 792-805.
[7] GENT A N. A new constitutive relation for rubber [J]. Rubber Chemistry and Technology, 1996, 69(1), 59-61.
[8] BOYCE M C. Direct comparison of the gent an the Arruda-Boyce constitutive models of rubber elasticity [J]. Rubber Chemistry and Technology, 1996, 69(5): 781-785.
[9] KILIAN H G. Equation of state of real networks [J]. Polymer, 1981, 22: 483-492.
[10] VILGIS T, KILIAN H G. The van der waals-network: A phenomenological approach to dense networks [J]. Polymer, 1984, 25(1): 71-74.
[11] OGDEN R W. Large deformation isotropic elasticity: On the correlation of theory and experiment for incompressible rubberlike solids [J]. Proceedings of the Royal Society of London, 1972, 326(1567): 565-584.
[12] 刘滢滢, 邢誉峰. 超弹性橡胶材料的改进Rivlin模型[J].固体力学学报, 2012, 33(4): 408-414. LIU Yingying, XING Yufeng. An improved Rivlin model of hyperelastic rubber materials [J].Chinese Journal of Solid Mechanics, 2012, 33(4): 408-414.
[13] 硫化橡胶或热塑性橡胶拉伸应力应变性能的测定: GB/T 528—2009 [S]. 北京: 中国标准出版社, 2009. Rubber, vulcanized or thermoplastic: Determination of tensile stress-strain properties: GB/T 528—2009 [S]. Beijing: Standards Press of China, 2009.
[14] 硫化橡胶或热塑性橡胶压缩应力应变性能的测定: GB/T 7757—2009[S].北京: 中国标准出版社, 2009. Rubber, vulcanized or thermoplastic: Determination of compression stress-strain properties: GB/T 7757—2009 [S]. Beijing: Standards Press of China, 2009.
港珠澳大桥主体工程贯通 世界最长、埋入海底最深
2017年7月7日上午10时,在东人工岛的海底隧道入口处,港珠澳大桥主体工程海底隧道正式贯通,这意味着港珠澳大桥主体工程正式贯通。待各工程陆续收尾后,港珠澳大桥预计将于年底达到通车条件。
港珠澳大桥是连接香港、珠海和澳门的超大型跨海通道,集桥、岛、隧于一体,全长55 km,是世界上最长的跨海大桥,也是中国建设史上里程最长、投资最多、施工难度最大的跨海桥梁。继2016年9月主体桥梁贯通后,迄今为世界最长、埋入海底最深、单个沉管质量最大、设计使用寿命最长、综合技术难度最大的沉管隧道。
海底兜圈感觉“太舒适”
隧道全程都有送风系统,空气不会比陆地上差。送风系统的管子底部特别设计了无数个小洞,可将陆地空气送进来,与隧道内部空气进行交换,但因海底环境的独特性,隧道内部温度将一年四季保持在23 ℃~25 ℃,可谓“四季如春”。
海底沉管隧道突破极限
因伶仃洋航道通航和空中航道等限制,港珠澳大桥设计了海底隧道,通过东西人工岛与桥梁连接。港珠澳大桥沉管隧道是21世纪该领域突破极限的综合性工程,主要表现在“超长”(在此之前全世界最长的海底公路沉管隧道只有4 km)、“超宽”(双向3车道)、“超深”(海底最深处近48 m)、“超复杂边界条件”(地处珠三角河口,太多恶劣的海洋工况,如超厚回淤等,给沉管隧道设计施工带来诸多挑战)。
通车后将“打通”粤西
深中通道等新工程即将开建,港珠澳大桥的功能是否会受影响?2座大桥的走向、功能不一样。深中通道连接的是中山与深圳,不能代替港珠澳大桥,各自将发挥不同的功能。
港珠澳大桥落成后,珠江三角洲西岸地区将纳入香港方圆3 h车程可达范围内。如珠海至香港葵涌货柜码头,现车程约200 km,需约3.5 h,大桥建成后路程将缩短为65 km,需时仅75 min,路程和行车时间减幅超过60%。
据分析,大桥通车后,香港旅游、金融和商业等不同范畴都会得益。尤其是来自珠三角西部、广东西部和广西等地的货物更能利用本港的机场和货柜码头,使香港作为贸易和物流枢纽的地位得以提升,并使香港国际机场和东涌新市镇产生协同效应。同时还将为香港、珠海和澳门三地间开通一条全新和直达的陆路连接通道,可大幅缩短陆路客运和货运往返香港、珠海及澳门三地的路程,避免绕道行驶并有助于减少汽车废气排放。
(摘自 21CN新闻 http://news.21cn.com/hot/gd/a/2017/0707/14/32463353.shtml)
Experimental Study of Constitutive Parameters of Ethylene-Propylene-Diene Monomer (EPDM) Rubber Gasket Used in Shield Tunnel
QIN Zhenggui1, 2
(1.CollegeofCivilandTransportationEngineering,HohaiUniversity,Nanjing210098,Jiangsu,China; 2.ChinaRailwayLiuyuanGroupCo.,Ltd.,Tianjin300308,China)
In order to rationally determine the constitutive model of ethylene-propylene-diene monomer (EPDM) elastic rubber gasket used of joints in shield tunnel and its parameters, a CMT4304 electronic universal testing machine controlled by microcomputer is adopted so as to complete the uniaxial tension and uniaxial compression test; and ABAQUS is used to analyze the experimental data. Considering the compliance and the stability of the material, the optimal constitutive model of the commonly used EPDM rubber material and its parameters are recommended. The results show that: 1) The Arruda-Boyce or van der Waals constitutive model is proposed to describe the EPDM rubbers with Shore hardness of 45 HA and 60 HA. 2) The Arruda-Boyce or Yeoh constitutive model is proposed to describe the EPDM rubber with Shore hardness of 55 HA. 3) The Mooeny-Rivlin constitutive model is proposed to describe EPDM rubber with Shore hardness of 65 HA.
shield tunnel; ethylene-propylene-diene monomer (EPDM) rubber; waterproof; constitutive model; Shore hardness
2016-11-03;
2017-04-21
秦正贵(1981—),男,湖南衡阳人,河海大学岩土工程专业在读博士,高级工程师,主要从事隧道及地下工程勘察设计和研究工作。E-mail: qzghhu@163.cm。
10.3973/j.issn.1672-741X.2017.07.006
U 454
A
1672-741X(2017)07-0816-06

