压电材料全矩阵材料常数超声谐振谱反演技术中的变温模式识别∗

汤立国

(厦门大学,水声通信与海洋信息技术教育部重点实验室,厦门 361102)

压电材料全矩阵材料常数超声谐振谱反演技术中的变温模式识别∗

汤立国†

(厦门大学,水声通信与海洋信息技术教育部重点实验室,厦门 361102)

(2016年9月20日收到;2016年10月18日收到修改稿)

利用传统的超声脉冲-回波与电谐振技术定征压电材料全矩阵材料参数,必须采用多块尺寸差异显著的样品,故很可能导致定征结果不自洽.超声谐振谱(RUS)技术仅需一块样品即可对压电材料全矩阵材料参数进行定征,故可确保定征结果的自洽.由于实际测量谐振谱中模式混叠与遗漏现象不可避免,使得谐振谱中谐振模式的准确识别成为RUS技术顺利实施的最大难点.本文提出一种谐振模式的变温识别技术.温度变化可导致压电体材料参数发生变化,材料参数的改变可影响各谐振模式的振动频率,且对不同谐振模式影响不一致,因此改变测量环境温度,有可能使得所测量超声谐振谱中某些原本混叠的模式分开或使得某些原本遗漏的模式出现.压电陶瓷(PZT-8)的实验结果表明,该技术可有效提高谐振谱中谐振模式识别准确率,从而保证了RUS反演的可靠性.

压电材料,材料常数,超声谐振谱,变温模式识别

1 引 言

压电材料无论在民用还是军用领域,皆有着广泛应用[1,2],如工业检测超声与医疗超声设备中的超声压电换能器及水声工程中水声压电换能器的核心材料皆为压电材料.压电材料在制备完成之后,首先必须对其材料参数进行定征,方能用于换能器的设计.若利用错误的材料参数进行压电换能器的模拟设计,很可能导致错误的结果,因此对压电材料全矩阵材料参数进行精确定征尤为重要.

目前,定征压电材料全矩阵材料参数最普遍的方法是超声脉冲-回波与电谐振技术[3-5].利用上述方法定征压电材料的全矩阵材料参数,需多块尺寸差异显著的样品,从不同样品可分别定征出若干个材料参数,如从d31振子可得恒电场顺度系数横向机电耦合系数k31,压电应变系数d31及自由介电常数而从d33振子可得恒电位移顺度系数横向机电耦合系数k33,恒电场顺度系数及压电应变系数d33,最后将从不同样品得到的参数进行综合可得全矩阵材料参数[6].尺寸差异显著的不同压电振子极化程度往往不一样,如薄片状的d31振子显然比杆状的d33振子更易极化,而极化程度不同将导致样品材料参数存在差异.因此,利用多个样品定征出的压电材料全矩阵材料参数很有可能不自洽[7-9].

欲保证所定征全矩阵材料参数自洽,采用样品数目必须尽可能少,最理想定征是所有参数来自于同一块样品.迄今为止,能够实现仅用一块样品即可定征压电材料全矩阵材料参数的方法有两种：超声谐振谱(RUS)技术[9-13]与电阻抗谱技术[14].与RUS技术相比,利用电阻抗谱技术定征材料参数效率较低,因为在反演迭代过程中需不断调用有限元软件计算样品电阻抗谱,而计算频率分辨率足够高的电阻抗谱非常耗时.RUS技术的基本原理如下：利用两个超声换能器顶住长方体样品的两个对角或圆柱体样品的边沿,扫频信号经功率放大器放大后驱动发射换能器产生振动,接收换能器所接收样品振动时域信号经傅里叶变换后即可得到样品的超声谐振谱,对该谱进行模式识别可得到样品的若干谐振频率;样品的谐振频率决定于样品的几何及材料参数,其中几何参数可直接测量得到,反之,由所测若干谐振频率可对样品的材料参数进行反演.RUS技术最初由Frazer与LeCraw[15]引入材料学领域进行固体弹性常数的反演.该技术曾被成功应用于月球岩石样品材料参数的精确反演.Ohno[10]最先将RUS技术引入压电体材料参数的反演.Ogi等[16,17]与Nakamura等[18]利用RUS技术对铌酸锂(LiNbO3),硅酸镓镧(La3Ga5SiO14),α-石英(α-SiO2)等机械品质因子QM值非常高的压电材料的弹性及压电常数进行了反演.Tang与Cao[9,19]利用变温RUS技术获得了自洽的PZT-4压电陶瓷及锰掺杂0.24Pb(In1/2Nb1/2)O3-0.46Pb(Mg1/3Nb2/3)O3-0.30PbTiO3单晶随温度变化的全矩阵材料参数.

RUS技术实施的最大难点在于对所测超声谐振谱进行分析并识别出足够多谐振模式,此为样品材料参数正确反演的基础.一般,材料独立参数越多,模式识别与反演难度越高.然而,在超声谐振谱测量过程中,谐振模式的遗漏与混叠几乎不可避免,其对模式识别造成极大干扰.在RUS技术实施过程中,允许模式遗漏与模式混叠现象的发生,进行参数反演时,舍弃这些模式即可,但是在进行参数反演时,各模式的次序必须明确,因此必须明确何处发生了模式遗漏及模式混叠,否则将无法对谐振谱中各模式的次序作准确识别.

本文提出一种谐振模式的变温识别方法.温度变化可导致样品材料参数发生变化,而材料参数的变化往往导致各模式谐振频率发生改变,然而各材料参数的变化对不同谐振模式的影响并不一致,因此在温度T1下混叠的模式在温度T2下可能分开,原本遗漏的模式也有可能出现.谐振模式的变温识别方法正是基于此.压电陶瓷(PZT-8)样品的变温超声谐振谱测试实验结果表明,通过变温可有效提高模式识别效率,从而确保了后续材料参数的正确反演.

2 压电体本征振动理论简介

压电体的Lagrangian量可表示为

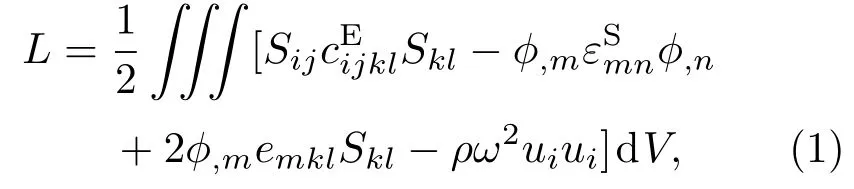
其中,Sij是应变张量分量,是恒电场弹性刚度系数,φ是电势,是自由介电常数,emkl是压电系数,ρ是密度,ω是角频率,ui是位移分量.位移ui与电势φ可展开为

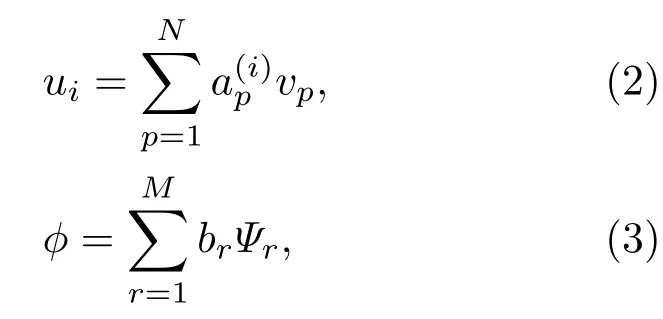
其中,{vp}与{Ψr}为正交基函数,本文数值计算中采用Legendre函数作为正交基函数,与br为展开系数.利用Rayleigh-Ritz方法,可得压电体本征振动方程：

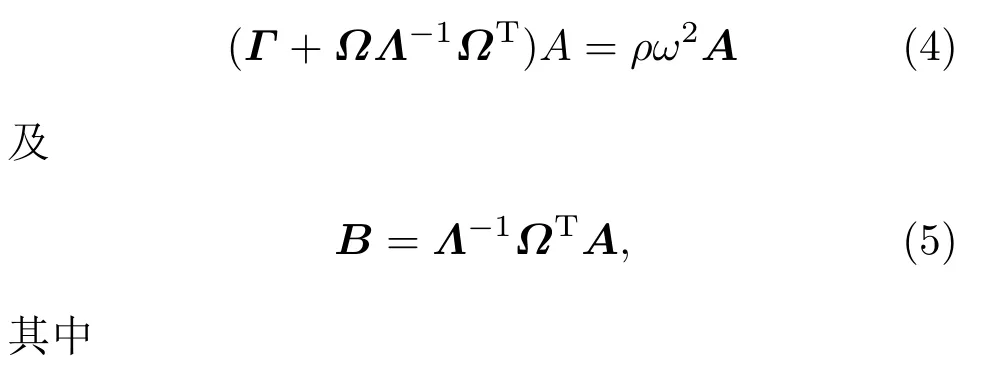
3 模式识别障碍与变温模式识别

对于PZT-8长方体样品,其振动模式根据对称特征可分为Ag,Bg,Au及Bu四大类[20].图1为PZT-8长方体样品谐振模式Ag-8-Ag-10,Au-8-Au-10,Bg-8-Bg-10,及Bu-8-Bu-10的频率随恒电场弹性常数与及压电应力常数e15与e33的变化关系.样品尺寸为4.8 mm×5.4 mm×5.0 mm,密度为7600 kg/m3.进行数值求解时,改变某个参数的值,其他材料参数如表1所示.

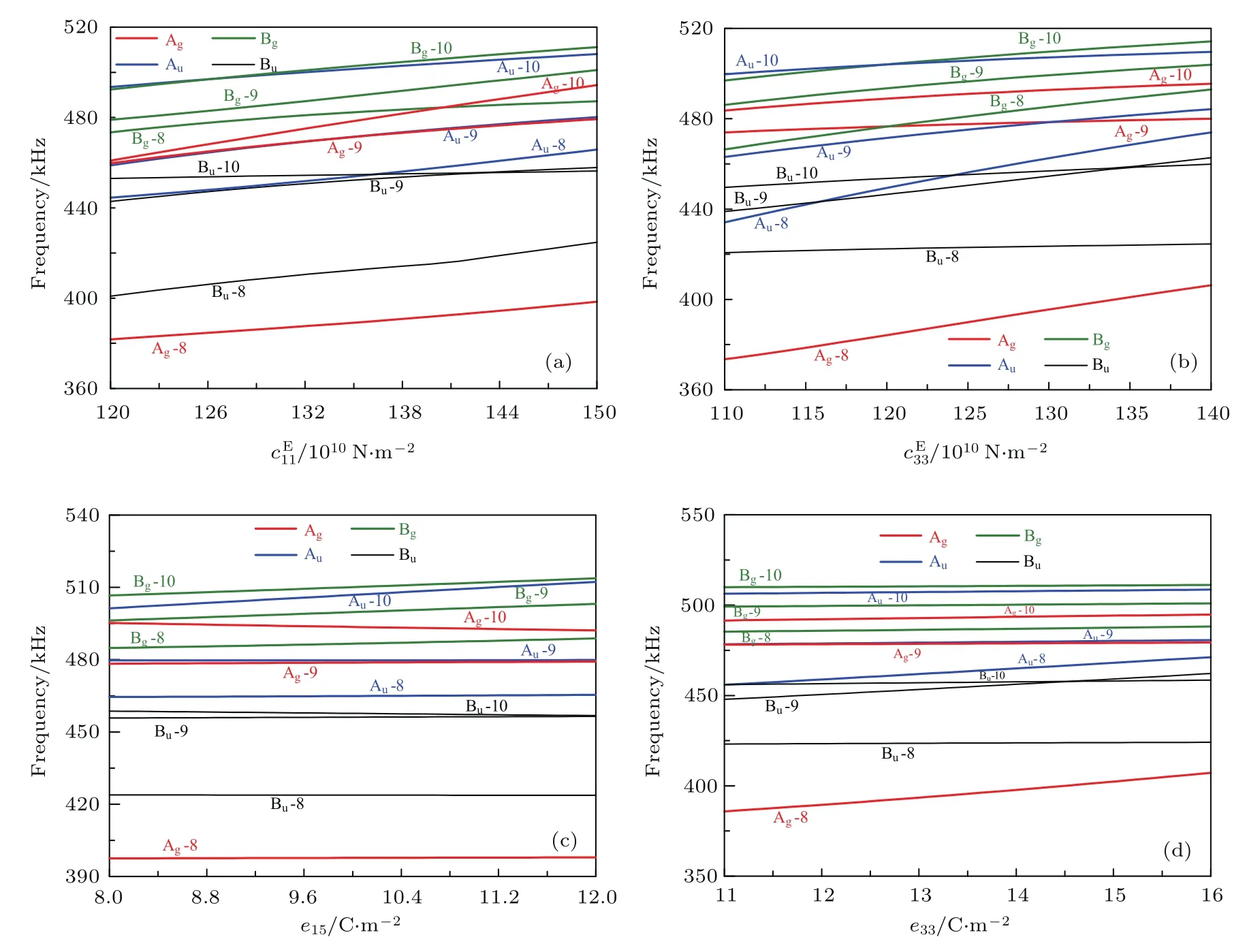
图1 材料常数变化对谐振频率的影响Fig.1.Resonance frequencies as functions of elastic and piezoelectric constants：(a)

表1 PZT-8材料常数Table 1.Material constants of PZT-8.

3.1 模式识别障碍分析

在RUS技术实施过程中,为保证反演结果的正确,首先必须对所测超声谐振谱中谐振模式进行准确识别,此为RUS技术实施的最大障碍与难点.一般,材料独立参数越多,模式识别与反演难度越高,因为独立参数越多,所需反演模式数目越多.由图1(a)可知,当在图示的范围内变化时,Ag-9与Au-9模式,Bg-10与Au-10模式始终非常接近,当约为13.6×1010N/m2时,Bu-9,Bu-10,Au-8模式非常接近.不同谐振模式频率非常接近的现象由图1(b)-图1(d)亦可观察到.进行超声谐振谱测量时,上述相邻且非常接近的模式易混叠在一起而难以识别.此外,实际测量过程中,有些模式振动非常弱,接收信号的信噪比很低,在谐振谱中无法观察到该模式的谐振峰,因此虽然该模式未与相邻模式发生混叠,但依然无法识别.利用RUS技术进行材料参数反演时,允许模式的遗漏,但是所识别各模式的次序必须明确,即必须明确何处发生了模式混叠及遗漏,否则将无法对谐振谱中所识别各谐振频率进行准确排序.

3.2 变温模式识别

一般,温度变化可导致压电样品材料参数发生变化,而材料参数的变化往往导致各谐振模式频率发生改变,且各材料参数的变化对不同谐振模式的影响并不一致.例如,由图1(a)可知,与模式Bg-8相比,模式Ag-10对的变化更加敏感;由图1(c)可知,与模式Au-9或Ag-9相比,模式Au-10对e15的变化更加敏感.正是由于材料参数变化对不同谐振模式的影响不一致,使得超声谐振谱的变温模式识别成为可能,因为温度T1下所测谐振谱中混叠的模式,在温度T2下所测谐振谱中有可能分开而变得易于识别.此外,温度改变导致材料常数发生改变,亦有可能导致实际测量中,不同模式的振动强度发生改变,从而使得原先振动很弱以至于在谐振谱中无法识别的模式,振动得到加强而易于识别.

超声谐振谱测试系统如文献[9]中图1所示.系统采用DRS Q9000超声谐振谱测试仪测试样品的谐振谱.图2为PZT-8长方体样品在20与80°C环境下所测得超声谐振谱图.样品尺寸为5.195 mm×4.818 mm×5.318 mm,密度为7550 kg/m3.由图2(a)可知,当温度T=20°C时,谐振谱中Bg-4与Ag-6模式谐振频率非常接近,彼此混叠而易被误判成仅有一个模式,当T=80°C时,材料参数发生了改变,且材料参数变化对该两个模式影响不一致,此二模式逐渐分离,而变得易于识别.由图2(b)可知,当温度T=20°C时,谐振谱中模式Au-9虽然未与相邻模式发生混叠,但是由于振动非常弱而无法识别,但当温度T=80°C时,模式Au-9的振动得到了加强而非常容易识别,此外,随着温度升高,Bg-8模式振动亦得到了加强.由图2(c)可知,随着温度升高,Bg-11模式振动得到了加强,谐振谱中该模式的谐振峰越显尖锐,而越易识别.

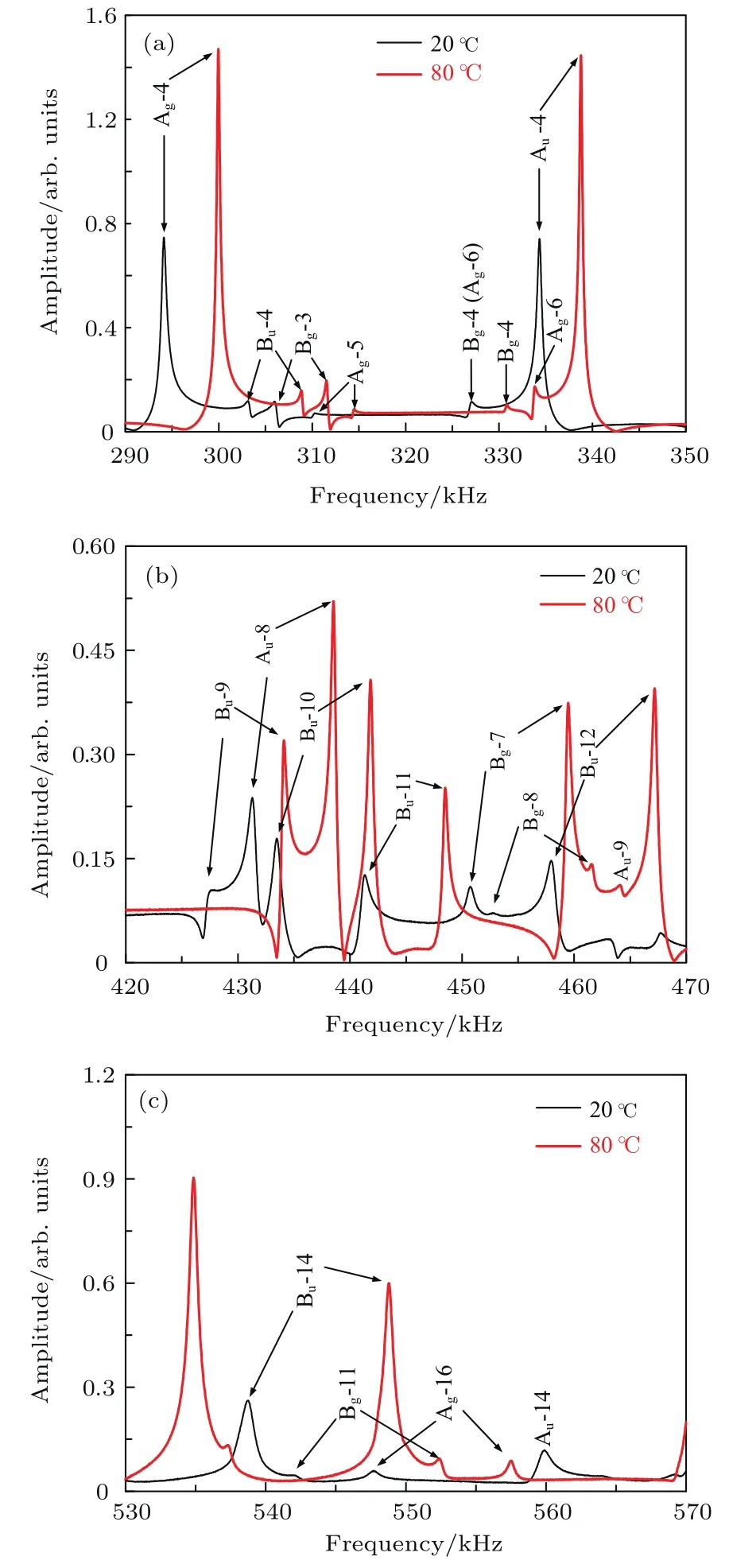
图2 PZT-8长方体样品在20与80◦C环境下所测得超声谐振谱图 (a)290-350 kHz;(b)420-470 kHz;(c)530-570 kHzFig.2.Resonant ultrasound spectra of a PZT-8 sample measured at 20 and 80◦C：(a)290-350 kHz;(b)420-470 kHz;(c)530-570 kHz.

4 PZT-8样品谐振谱模式识别与参数反演

由于PZT-8样品谐振模式频率对介电常数的变化非常不敏感,如图3所示,故介电常数无法利用RUS技术反演,但是,可利用阻抗分析仪测得的电容直接计算得出.本文所采用PZT-8样品的夹持介电常数测量结果为3.2小节中所述样品的谐振模式识别结果如表2所列,其中,fmeas为从所测超声谐振谱中识别出的各谐振模式频率.表3为弹性刚度系数及压电应力系数反演结果.根据反演结果所计算恒电位移弹性刚度系数和的值分别为15.02×1010及3.850×1010N/m2,利用超声脉冲-回波技术测量所得和的值分别为15.08×1010及3.832×1010N/m2,相对误差皆小于0.5%,表明了反演结果的自洽.表2中fcal为根据反演结果所计算各谐振模式频率,其与测量结果非常一致,相对误差大多小于0.3%.

图3 介电常数变化对谐振频率的影响Fig.3.Resonance frequencies as functions of dielectric constants：

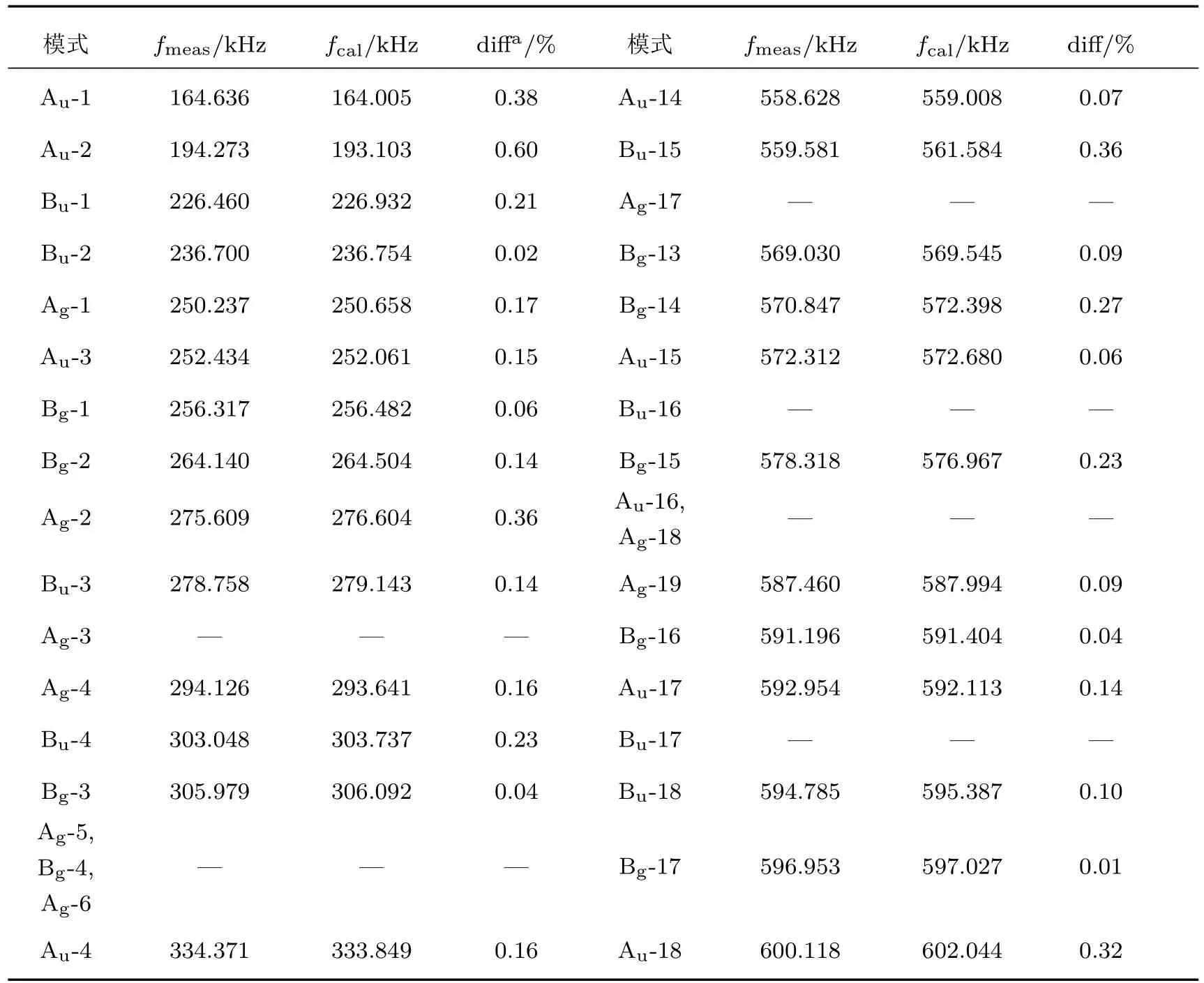
表2 实测及计算所得谐振频率Table 2.Measured and calculated resonance frequencies.

表2 实测及计算所得谐振频率(续)Table 2.Measured and calculated resonance frequencies(continued).

若相邻模式混叠在一起,则难以从谐振谱中将各自的谐振频率准确读出,故反演时,舍弃了如Bg-4与Ag-6之类混叠在一起的模式.若将图2(a)中混叠在一起的Bg-4与Ag-6两个模式误判为一个模式,则导致后续模式的排序错误,表4为该错误排序下的反演结果.虽然仅仅排序时漏了一个模式,但是e15的反演结果与正确结果相对误差达到了38%,e33的反演结果与正确结果的相对误差达到了27%.总而言之,识别模式排序的错误将直接导致反演的失败,而谐振模式的变温识别技术将有效提高模式的识别准确率.

表3 PZT-8材料常数反演结果Table 3.Inversion results of PZT-8.

表4 排序有误时的反演结果Table 4.Inversion results from the resonance frequencies with wrong order.

5 结 论

与传统的超声脉冲-回波与电谐振技术相比,RUS技术最大优点在于仅需一块样品即可定征压电材料全矩阵材料参数,从而确保了定征结果的自洽.然而,实际测量所得超声谐振谱中谐振模式混叠与遗漏现象不可避免,使得谐振模式的准确识别成为RUS技术顺利实施的最大难点,且材料独立参数越多,模式识别与反演难度越高.提高模式识别效率与准确率一直是该领域研究重点之一.本文提出一种谐振模式的变温识别技术.PZT-8样品的实验结果表明,该技术可有效提高谐振谱中谐振模式识别准确率.需指出,变温识别技术并不能彻底解决模式识别问题,将不同的识别技术结合起来,如多点测振与变温识别,以提高模式识别的准确度将是进一步需要展开的研究.

感谢美国宾夕法尼亚州立大学曹文武教授为本文测试及分析所提供的帮助.

[1]Muralt P 2000J.Micromech.Microeng.10 136

[2]Zhou Q F,Lam K H,Zheng H R,Qiu W B,Shung K K 2014Prog.Mater.Sci.66 87

[3]Zhang S J,Li F 2012J.Appl.Phys.111 031301

[4]Zhang S J,Lee S M,Kim D H,Lee H Y,Shrout T R 2008J.Am.Ceram.Soc.91 683

[5]Sun E W,Zhang R,Wu F M,Cao W W 2013J.Alloys Compd.553 267

[6]Sun E W 2011Ph.D.Dissertation(Harbin：Harbin Institute of Technology)(in Chinese)[孙恩伟 2011博士学位论文(哈尔滨：哈尔滨工业大学)]

[7]Topolov V Y 2010Appl.Phys.Lett.96 196101

[8]Topolov V Y,Bowen C R 2011J.Appl.Phys.109 094107

[9]Tang L G,Cao W W 2015Appl.Phys.Lett.106 052902

[10]Ohno I 1990Phys.Chem.Miner.17 371

[11]Leisure R G,Willis F A 1997J.Phys.:Condens.Matter9 6001

[12]Zadler B J,Rousseau J H L,Scales J A,Smith M L 2004Geophys.J.Int.156 154

[13]Migliori A,Maynard J D 2005Rev.Sci.Instrum.76 121301

[14]Li S Y,Zheng L M,Jiang W H,Sahul R,Gopalan V,Cao W W 2013J.Appl.Phys.114 104505

[15]Frazer D B,LeCraw R C 1964Rev.Sci.Instrum.35 1113

[16]Ogi H,Kawasaki Y,Hirao M,Ledbetter H 2002J.Appl.Phys.92 2451

[17]Ogi H,Ohmori T,Nakamura N,Hirao M 2006J.Appl.Phys.100 053511

[18]Nakamura N,Ogi H,Hirao M 2012J.Appl.Phys.111 013509

[19]Tang L G,Tian H,Zhang Y,Cao W W 2016Appl.Phys.Lett.108 082901

[20]Mochizuki E 1987J.Phys.Earth35 159

PACS:77.84.-s,43.35.+d,43.35.Yb DOI:10.7498/aps.66.027703

Mode identification via temperature variation in resonant ultrasonic spectroscopy technique for piezoelectric material∗

Tang Li-Guo†
(Key Laboratory of Underwater Acoustic Communication and Marine Information Technology,Ministry of Education,Xiamen University,Xiamen 361102,China)

20 September 2016;revised manuscript

18 October 2016)

The full matrix material constants of piezoelectric materials should be characterized first before they have been used to make actuators or sensors.Up to now,they are usually determined by the ultrasonic pulse-echo and electric impedance resonance techniques through using multiple samples with drastically different sizes.However,the constants determined by the aforementioned techniques are probably inconsistent because the sample-to-sample variation cannot be eliminated.The technique of resonant ultrasonic spectroscopy(RUS)only needs one sample to determine the full matrix constants of piezoelectric material.Therefore,the consistency of the constants is guaranteed.During the implementation of the RUS technique,the elastic stiffnessand piezoelectric constantseijcan be determined from the resonance modes identified from the resonant ultrasonic spectrum.The free and clamped dielectric constants cannot be determined by the RUS technique because they have very weak influence on resonance frequency.However,they can be directly measured from the same sample by using an impedance analyzer.To ensure the reliable inversion of material constants,enough resonance modes should be identified from the measured resonant ultrasonic spectrum.However,there are many missing and overlapped modes in the spectrum,which makes mode identification become a biggest obstacle to the implementation of the RUS technique.The adjacent modes may overlap if the resonance frequencies corresponding to them have a very small difference.In addition,the lower the mechanical quality factorQM,the more likely to overlap the adjacent modes are.During the RUS measurement,the rectangular parallelepiped sample is placed between the transmitting and receiving transducers with contacts only at the opposite corners of the sample.Resonance modes would not be detected if the receiving point,i.e.,one corner of the sample,is the node of these modes.Therefore,there are missing modes in the resonant ultrasonic spectrum.To overcome the difficulty in identifying the modes,caused by modes missing and overlapping,the mode identifying method via temperature variation is presented in this study.Note that a change of temperature may change the material properties of a piezoelectric sample.The material properties have a great influence on the resonance frequency of the sample.Moreover,the influences corresponding to resonance modes are different.Therefore,the variation of temperature may make the overlapped modes separated from each other and the missing modes appear,namely,the missing and overlapped modes may be identified by comparing the resonant ultrasonic spectra measured at different temperatures.The experimental results of piezoelectric ceramics(PZT-8)show that this method can effectively improve the accuracy of mode identification and guarantee the reliability of inversion in the RUS technique.

piezoelectric materials,material constants,resonant ultrasonic spectroscopy,mode identi fication via temperature variation

:77.84.-s,43.35.+d,43.35.Yb

10.7498/aps.66.027703

∗国家自然科学基金(批准号：11374245,11674270)资助的课题.

†通信作者.E-mail：liguotang@xmu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11374245,11674270).

†Corresponding author.E-mail：liguotang@xmu.edu.cn