若干电磁波完全极化参数组的完备变换关系

刘俊群 刘耀文

(南京电子技术研究所,南京 210039)

若干电磁波完全极化参数组的完备变换关系

刘俊群†刘耀文

(南京电子技术研究所,南京 210039)

(2016年9月13日收到;2016年12月5日收到修改稿)

极化与电磁波另外的两个特性——振幅和相位,在传递信息时具有同等重要的作用,描述电磁波极化及其演化特征具有重要意义.关于电磁波的极化描述,前人针对不同边界条件和初始状态,发展了不同的参数组,但是这些参数组没有全面考虑电磁波的初相.鉴于此,全面考虑了电磁波的初相问题,对极化椭圆参数组的旋向参数也进行了扩充和完善,重新定义了这些参数组,在此基础上推导出这些参数组的相互变换关系,并借助符号数学数值与仿真计算验证了这些相互变换关系的正确性.结果表明这些全面包含初相的电磁波完全极化参数组是完备的,相互之间具有一一对应的关系.给出的参数组变换关系显著地简化了繁杂的电磁波极化计算过程,为电磁波极化理论和应用设计提供了更加完备、适用的方案,具有理论参考和应用价值.

电磁波,完全极化参数组,变换关系

1 引 言

在电磁波的传播过程中,无论场的振幅、相位或极化都包含有信息量,可以用来传递信息.这一特性赋予了电磁波极强的信息承载和传播功能,其重要性和巨大成效历经一个多世纪的积淀与发展,依然日久弥新.极化是电磁波的一个基本特性,其传播信息的重要性不断提升,应用领域不断拓展.但是,电磁波极化的准确预测计算依然存在一些问题,本文主要关注不同初始与边界条件下电磁波极化的计算方法.

电磁波的极化一般定义为空间中一固定点上电场矢量E的空间取向随时间变化的方式.极化按纯度可分为完全极化、非极化和介于二者之间的部分极化[1].王雪松等在1999年针对宽带电磁波提出瞬态极化理论,这一理论涵盖了完全极化理论,假定每一时刻瞬态极化电磁波为完全极化[2],该理论与实际表征结果十分符合,表明这一假设的有效性,也说明完全极化理论的研究具有理论参考或指导意义.

众所周知,电磁波极化的应用范围十分广泛.从本质上讲,极化特性是电磁波产生空间各向异性的根本原因.调幅电台发射的电磁波在远区可近似为垂直于地面的垂直极化波,电视信号则采用水平极化波.很多情况下,为了避免电磁波穿过雨层出现过大损耗,又倾向于采用圆极化波.同样地,不论是遥控火箭还是卫星,只要是针对运动系统,一般均采用圆极化波——它可以转换分解成两个线极化波的叠加,不论检测哪部分线极化波,总有一部分分量可以被接收,利于实际控制[3].另外,在雷达信号滤波、检测、增强、抗干扰、目标鉴别/识别等方面,电磁波极化特性的利用都展示出巨大的应用潜力[4−6].理论上讲,目标、干扰和杂波在极化域中的特性差异构成了极化信息处理的物理基础,特别是当两个信号在时域、频域以及空域的特征都很接近时,就可以或者也只能利用两者在极化域的差异来进行有效区分.

电磁波极化特性的应用研究离不开理论支撑,电磁波吸波材料或超材料的设计、仿真和实验研究都将极化作为一个基本特性参数进行研究[7−11].文献[7]设计了一种基于各向异性介质特性的电磁波变极化结构,该电磁波属于完全极化电磁波.要利用电磁波的极化信息,需要对其进行完备的描述.完全极化理论大多采用矢量正交分解方法来分析,尤其是用彭加勒球来描述波的极化特性,为描述极化特性提供了一种统一的处理方案和直观的几何图像.而这一描述方案的主要对象是定态(简谐)平面电磁波,它是电磁波波动方程的基本解,其极化状态具有基本的物理意义.

要描述平面电磁波的极化状态,首先需要一组描述极化的参数组.不同的研究小组针对不同具体情况提出和发展了不同的参数组,形成了电磁波极化特性研究纷呈复杂的局面.这些参数组都可以基本确定极化的特征,即极化椭圆(polarization ellipse,PE)的轴比、倾角、旋向、初相等.对这些参数组进行梳理,发现最为人熟知的是Stokes参数组.该参数组将各种描述极化特性的方法融合在一起,普适性很强,计算效率高,一直是实际应用研究的热点[12−14].文献[15,16]应用概率统计理论对随机分布的瞬态极化的两种极化参数组,即PE参数组和Stokes参数组,进行了深入分析.至今为止,最为常见的参数组有五类.

1)正交线极化(orthogonal linear polarization,OLP)参数组在空间垂直于z轴的平面内任选两个正交方向1和2,其基矢分别为u1和u2,则电场表达式为

式中(E1m,E2m)为方向(1,2)的电场振幅(非负数,下同),为沿u1和u2方向的电场分量初相,为初相差,ω和k为角频率与波数,t为时间,z为沿电磁波传播方向的坐标,传播方向的基矢可以表示为uz=u1×u2.但文献[17,18]中提出的OLP参数组并没有包括初相ϕL,从而使得这一参数组缺乏初相信息.这里的初相参数是本文基于完备性考虑而添加的.

2)正交斜极化(orthogonal diagonal polarization,ODP)参数组设定另外一组正交方向(3,4),其基矢为(u3,u4).这一组正交系与(1,2)正交系45◦斜交.在(u3,u4)正交系中,(E3m,E4m)为沿着(3,4)方向的电场振幅,为对应电场分量初相,为对应的初相差,传播方向的基矢也可以表示为uz=u3×u4.则电场可以写为

3)正交圆极化(orthogonal circular polarization,OCP)参数组为左旋和右旋圆极化的电场振幅分量(二者旋向相反),为对应的电场分量初相,δC=为对应的初相差.这一参数组定义下的电场表达式与(1),(2)式类似,不再专门写出.

4)PE参数组(a,b,τ,χ′,x0,y0).a为椭圆长半轴,b为椭圆短半轴,τ为椭圆倾角,χ′为包含完备旋向信息的数字化椭圆角参数,(x0,y0)为本参数组的初始运动点(即初相信息).同样,文献[17,18]中提出的PE参数组并没有包括初相(x0,y0),这里的两个初相参数是基于完备性考虑而添加的.

5)Stokes参数组(YL,XL,YD,XD,YC,XC).这是一类具有普适性的参数组,与彭加勒球结合起来可以给出前三种正交极化的分量极化比和初相差.这里不涉及初相,六个参数的具体定义将在2.1节加以说明.

在不考虑基于完备性提出添加的上述三个初相参数和数字化椭圆角参数χ′的情形下,这些参数组在实际应用时有一些问题和不足.例如,文献[17,18]中提出的OLP参数组和PE参数组都没有完备地讨论初相参数,因此分量之间的时间相位关系缺乏完备性或无从确定.同时,PE参数组还缺乏线极化旋向的描述.本文重点在于两个方面:一方面,进一步完善已经提出的参数组,包括引入新的初相参数(即ϕL,x0,y0),同时,对PE参数组引入数字化椭圆角参数χ′来代替原来的椭圆角参数χ,以完善线极化的旋向信息;另一方面,每一组参数组都必须是电磁波极化状态的完备描述组.由于在OLP和PE参数组中引入了初相参数和数字化椭圆角参数,各参数组之间的变换关系必须重新加以求解.同时还要考察参数组是否描述完备,参数组之间的一一对应性是否成立,如果参数组本身不完备或者参数组之间非一一对应,则表明参数的选择需改进.这些添加了初相和数字化椭圆角参数的参数组之间的变换关系鲜有文献报道.本文的主要内容即是针对上述两个方面开展研究.

2 参数组变换关系

2.1 Stokes参数组

在上述五类参数组中,Stokes参数组是极化理论研究的纽带,分析这些参数组相互关系时可以Stokes参数组为联系桥梁.为此,首先给出Stokes参数组各参数的定义,其表现为与正交参数组中电磁波电场幅值之间的关系[18]:

其次,Stokes参数组与正交参数组初相差有如下关系:

2.2 OLP参数组与PE参数组的变换关系

OLP参数组和PE参数组是描述极化状态最常见的参数组,因此先分析它们之间的变换关系.从对应的两组参数组和(a,b,τ,χ′,x0,y0)出发,设有一沿z方向传播的无衰减均匀平面波,根据正交分量约定,应用约束条件则(1)式的瞬时电场矢量E(z,t)可写为

式中采用直角坐标系,变量名为Ex(z,t),Ey(z,t),分别表示(1,2)方向的电场分量,(6)式消去ωt-kz,可得Ex(z,t)和Ey(z,t)的二元二次方程:

该方程经过坐标系旋转变换,可以得到标准椭圆方程,椭圆方程参数a和b为

对于PE参数组(a,b,τ,χ,x0,y0),椭圆角参数χ暂选文献[17]的含义,第三个参数是椭圆倾角τ.如果规定τ∈(−π/2,π/2],由坐标系旋转变换得

(10)式中β表示该范围内的任意实数.

参数χ描述椭圆运动旋向,其绝对值由a,b决定,其符号决定了PE旋向,满足[17]

这里用符号值作为独立变量,χ=0时表示线极化.但是丢失了线极化的旋向,即初始运动方向信息.为了排除这一奇异点,引入一个更完备的数字化椭圆角参数χ′,考虑了线极化时初始运动方向信息,包括非垂直线极化(即斜线极化和水平线极化)和垂直线极化两种情形.将这些因素结合在一起,可得

式中相位不考虑周期性,统一化为区间[−π,π)内的数值.从(12)式可以看到,χ′=1表示左旋椭圆或圆极化,χ′=−1表示右旋椭圆或圆极化,χ′=1/2表示初始沿x轴正向运动的斜极化或水平线极化,χ′=−1/2表示初始沿x轴负向运动的斜极化或水平线极化,χ′=1/4表示初始沿y轴正向运动的垂直线极化,χ′=−1/4表示初始沿y轴负向运动的垂直线极化.χ′的数值符号表示旋向,数值大小用于区分不同的极化形式,而为保持连贯性和方便起见,选择绝对值不大于1的相反数来表达更完备的旋向参数χ′,数值符号代表非线极化的旋向或线极化的初始运动方向,数值大小1表示与椭圆极化或圆极化相关,数值大小1/2表示与斜极化或水平线极化相关,数值大小1/4表示与垂直线极化相关,当然数值大小本身不再有其他物理含义.

最后讨论两个初相参数(x0,y0),它们对应初始时刻电场矢量的坐标,与OLP参数组定义的初相和相差有关.电磁波传播方向是z方向,因此初始时刻电场矢量沿z轴坐标可设定为z=0,由此得到

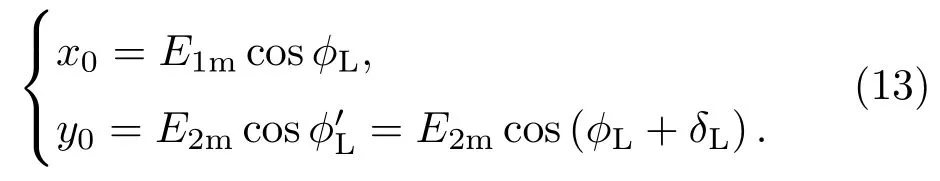
已知电场矢量端点处的PE参数组(a,b,τ,χ′,x0,y0),如图1所示.结合具体物理意义,从图1可知,作一垂直于x轴的直线,与椭圆交于两点.直线与x轴垂直,并沿x轴正向移动,当两交点重合为一点时,直线的x坐标位置为x1,x1对应电场幅值E1m.同理,另一直线与y轴垂直,沿y轴正向移动,两交点重合为一点时,其y坐标位置为y1,y1对应电场幅值E2m.由椭圆倾角τ的定义,原坐标系坐标(x,y)旋转角度τ后变成新坐标系坐标(x′,y′).在新坐标系中,椭圆成为标准椭圆,轨迹方程为

图1 PE参数组(a,b,τ,χ′,x0,y0)Fig.1.PE parameter group(a,b,τ,χ′,x0,y0).

坐标系旋转变换公式为

代入(14)式得原坐标系方程

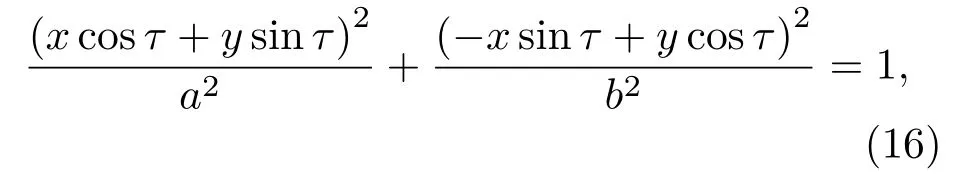
将(16)式分别看作y和x的一元二次方程,可得

(17)式适用于任意极化,在b=0时对应线极化.

上述过程的求解和计算可以借助美国科学计算软件矩阵实验室(MATLAB)的符号数学工具完成[19−24].不过,利用这一工具处理电磁波理论的详细工作并不多,文献[25]偏重于符号数学编程,文献[26]是处理电磁波问题的一个例子.

式中β表示该范围内的任意实数,可以得到

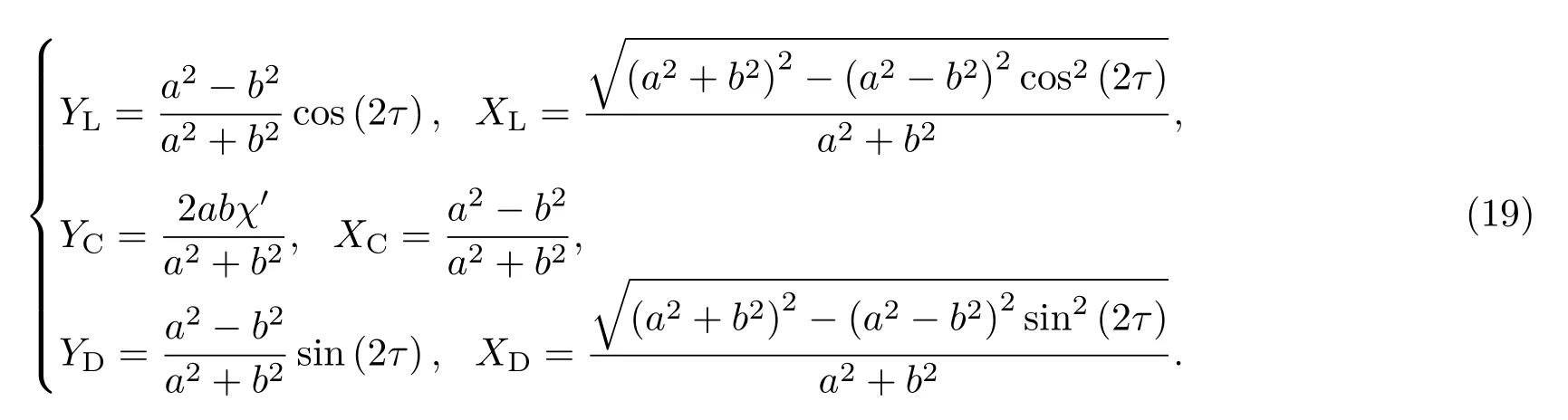
结合(5)式和(19)式,即求得δL:

求出δL之后,只需要确定OLP参数组中的ϕL或即可完成PE参数组(a,b,τ,变换为OLP 参数组的逆变换.这里的变换已经包括了初相信息,即所得参数组是完备的.为此,根据(13),(17)和(20)式,得到如下结果:

式中β′为该范围内的任意实数.

至此,由PE参数组(a,b,τ,χ′,x0,y0)变换为OLP参数组的完备公式如(17),(21),(22)三式所示,第3节中将给出一个实例来验证其正确性.

2.3 OLP参数组与ODP参数组、OCP参数组的变换关系

变换时比较简便的方法是利用简谐振动矢量的复矢量表示法,OLP参数组(E1m,E2m,ϕL,ϕ′L)的复矢量表示为

式中E为简谐振动矢量的复振幅,即E(z,t)=Re{Eexp[j(ωt−kz)]}. 根据ODP参数组和OCP 参数组的物理意义,对应的复矢量分别表示为

由(23)—(25)式,可以整理得到变换结果:

(26)—(28)式为OLP参数组变换为ODP参数组的变换结果.与此对应,OLP参数组变换为OCP参数组的变换结果为

3 数值仿真验证

为了进一步验证上述各参数组之间变换关系的正确性,利用MATLAB符号数学软件进行数值计算,以验证这些关系的正确性、完备性.选取实际应用中最常见的OLP参数组、OCP参数组和PE参数组之间的关系来进行计算验证.

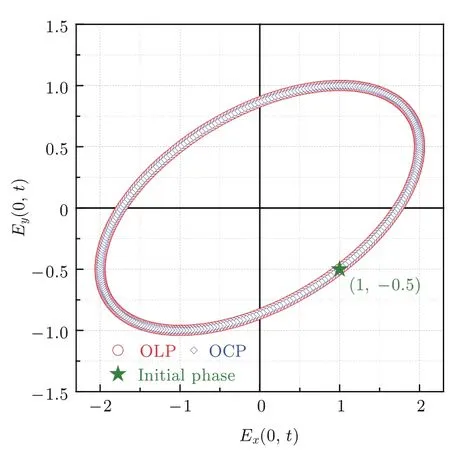
图2 (网刊彩色)OLP参数组变换为OCP参数组(EL=1.4547,ER=0.6197,Fig.2.(color online)The conversion of the OLP parameter groupto the OCP parameter group

PE参数组到OLP参数组的变换如(17),(21)和(22)式所示.对PE参数组,设a=2,b=1,τ=−30◦,χ′=−1,x0=−0.5,计算的电磁波轨迹如图3所示,初相点为经过变换所得OLP参数组数值为计算所得的电磁波轨迹也在图3绘出,图中还标出了初相所对应的轨迹点.从图3可以看到,PE参数组和OLP参数组所描述的PE轨迹完全符合,而且离散数据点横、纵坐标值也完全符合,表明上述求解变换公式完全正确.

在实际应用中,多数情况下都采用PE参数组来描述天线的极化特性,主要关注轴比(即a/b,值不小于1)、倾角τ、数字化椭圆角参数χ′[18].天线极化测量通常用直接或间接方法来确定这些参数.直接方法直接测出PE参数或其图形,间接方法是通过各种正交分解的参数组变换得出PE参数组.引入数字化椭圆角参数χ′和初相参数(x0,y0),既完备了参数组,又扩展了天线极化测量的应用领域.该变换方法是一种天线极化测量的间接方法.

图3 (网刊彩色)PE参数组(a=2,b=1,τ= −30◦,变换为OLP参数组Fig.3.(color online)The conversion of the PE parameter groupto the OLP parameter group

图4 (网刊彩色)OLP参数组1.3329,变换为PE参数组(对图3的逆变换)Fig.4.(color online)The conversion of the OLP parameter groupto the PE parameter group(a=2,b=1,referring to the inverse conversion shown in Fig.3.

实际应用需要对OLP参数组到PE参数组的变换关系式进行数值仿真验证.OLP参数组到PE参数组的变换如(8)—(13)式所示.仍取图3所示PE参数组变换为OLP参数组的算例,可进一步考察、验证变换的可逆性、唯一性.设E1m=1.8028,变换输出结果为a=2,b=1,τ=−30◦,χ′=−1,与图3输入的PE参数组结果完全一致,证明了变换的可逆性、唯一性,如图4所示.

4 结 论

本文全面推导了描述电磁波完全极化特性的不同参数组之间的相互完备变换关系.这些不同参数组都包含初相参数,其中PE参数组、OLP参数组的初相参数是为了理论和应用完备性而添加的.与此同时,还扩展完善了描述线极化时PE参数组的数字化椭圆角参数χ′,从而实现了任一参数组对完全极化特征的完备描述.基于符号数学的数值计算结果充分验证了这些严格的相互变换关系的正确性,揭示了各参数组之间的一一对应性,为这些全面包含初相参数的不同参数组之间的相互变换提供了有效、完备的计算公式,对极化理论和应用都具有参考价值.

[1]Lacaze B 2011Opt.Commun.284 2700

[2]Rao B,Xiao S P,Wang X S,Li Y Z 2011Journal of System Simulation23 2296(in Chinese)[饶彬,肖顺平,王雪松,李永祯2011系统仿真学报23 2296]

[3]Liang C H,Chen X 2011Journal of Electrical&Electronic Education33 1(in Chinese)[梁昌洪,陈曦2011电气电子教学学报33 1]

[4]Giuli D 1986Pro.IEEE74 245

[5]Zhuang Z W,Xiao S P,Wang X S 1999Radar Polarization Information Processing and Application(Beijing:National Defense Industry Press)pp1—20(in Chinese)[庄钊文,肖顺平,王雪松1999雷达极化信息处理及应用(北京:国防工业出版社)第1—20页]

[6]Wang X S 1999Ph.D.Dissertation(Changsha:National University of Defense Technology)(in Chinese)[王雪松1999博士学位论文(长沙:国防科技大学)]

[7]Chen L T,Chen Y Z,Nie Y,Gong R Z 2012Acta Phys.Sin.61 094203(in Chinese)[陈龙天,程用志,聂彦,龚荣洲2012物理学报61 094203]

[8]Zhou H,Qu S B,Peng W D,Wang J F,Ma H,Zhang D W,Zhang J Q,Bai P,Xu Z 2012Acta Phys.Sin.61 104201(in Chinese)[周航,屈绍波,彭卫东,王甲富,马华,张东伟,张介秋,柏鹏,徐卓2012物理学报61 104201]

[9]Tang Q,Meng F Y,Zhang K,Wu Q,Li L W 2011Acta Phys.Sin.60 014206(in Chinese)[汤奇,孟繁义,张狂,吴群,李乐伟2011物理学报60 014206]

[10]Campbell S D,Ziolkowski R W 2013IEEE Trans.Antenn.Propa.61 1191

[11]Huang L,Fan Y H,Wu S,Yu L Z 2015Chin.Phys.Lett.32 094101

[12]Vena C,Versace C,Bartolino R 2013EPL101 24003

[13]Hacyan S 2012Gen.Relat.Gravit.44 2923

[14]Wang T,Zhao D M 2012Opt.Commun.285 893

[15]Liu T,Huang G M,Wang X S,Xiao S P 2009Acta Phys.Sin.58 3140(in Chinese)[刘涛,黄高明,王雪松,肖顺平2009物理学报58 3140]

[16]Liu T,Wang X S,Xiao S P 2008Science in China Series E-Infomation Sciences38 2241(in Chinese)[刘涛,王雪松,肖顺平2008中国科学E辑:信息科学38 2241]

[17]Wang Y P 2007Engineering Eletrodynamics(2nd Ed.Revision)(Xi’an:Xidian University Press)pp186–192(in Chinese)[王一平 2007工程电动力学 (第2版修订本)(西安:西安电子科技大学出版社)第186—192页]

[18]Mao N H,Ju X D 1987Antenna Measurement Handbook(Beijing:National Defense Industry Press)pp126–168(in Chinese)[毛乃宏,俱新德 1987天线测量手册 (北京:国防工业出版社)第126—168页]

[19]Jia J T,Kong Q X,Sogabe T 2012Int.J.Comput.Math.89 851

[20]Sogabe T,El-Mikkawy M 2011Appl.Math.Comput.218 2740

[21]Liang J S,Chen Y Q,Guo B Z 2004Simul.-Trans.the Soc.Mod.Sim.80 635

[22]Zhang Y N,Yi C F,Ma W M 2009Simul.Model.Pract.T.17 1603

[23]Suman V,Datta D,Sarkar P K,Kushwaha H S 2010Indian Journal of Pure&Applied Physics48 787

[24]Yang Z H 2007Chaos Solutions&Fractals34 932

[25]Huang Y,Qian F X,Dong L X 2002Experiments and Measurements in Fluid Mechanics16 91(in Chinese)[黄勇,钱丰学,董立新2002流体力学实验与测量16 91]

[26]Boute R 2009IEEE Antenn.Propag.Mag.51 177

PACS:41.20.Jb,42.25.Ja,02.70.Wz DOI:10.7498/aps.66.054101

Conversion relationships between several parameter groups of completely polarized electromagnetic waves

Liu Jun-Qun†Liu Yao-Wen

(Nanjing Research Institute of Electronics Technology,Nanjing 210039,China)

13 September 2016;revised manuscript

5 December 2016)

It is known that polarization as the third characteristic of electromagnetic waves plays substantial roles which are comparable with the wave amplitude and phase,in describing the tempo and spatial properties of electromagnetic waves.Various parameter groups for characterizing the polarization state of electromagnetic waves with different initial states and boundary conditions have been proposed.However,a full-scale set of conversion relationships between these parameter groups with specific initial phases is not yet available.In this work,the initial phases as additional parameters for the orthogonal linear polarization and the polarization ellipse parameter groups and the digitized elliptical angleχ′as a complementary parameter to the polarization ellipse parameter group are taken into account respectively.Consequently,a full-scale set of conversion relationships between these parameter groups has been rigorously derived out.The validity of these conversion relationships are confirmed by the numerical calculations in terms of mathematical completeness and one-to-one correspondence.These conversion relationships make the tedious computation of the wave polarization much simpler and straightforward,benefiting practical implementation of the polarization theory of electromagnetic waves.

electromagnetic waves,parameter groups of complete polarization,conversion relationships

PACS:41.20.Jb,42.25.Ja,02.70.Wz

10.7498/aps.66.054101

†通信作者.E-mail:sufhap@sina.com

†Corresponding author.E-mail:sufhap@sina.com