MapReduce框架下近似概念格的并行构造算法*

谭富林，姜 麟

（昆明理工大学理学院，昆明650500）

·微机软件·

MapReduce框架下近似概念格的并行构造算法*

谭富林，姜 麟

（昆明理工大学理学院，昆明650500）

具有缺值的形式背景称为不完备形式背景，相应的概念格扩展模型称为近似概念格。近似概念格构造中，在数据规模大的情况下采用串行算法效率低，完备形式背景下概念格并行构造算法不适用于不完备形式背景。针对这些问题，对近似概念格的特征进行深入分析，提出了在MapReduce框架下的两种分布式构造算法，包括一种并行合并算法和一种增量式并行算法。实验结果表明，相比串行算法，两种并行构造算法可以提高近似概念格的建格效率。

不完备形式背景;近似概念格；概念格构造；MapReduce框架；并行构造算法

1 引言

MapReduce是Google公司提出的一种编程模型，广泛应用于数据挖掘、信息提取、机器学习等场景。MapReduce分布式处理框架具有容错控制、细节隐藏、伸缩性好等优点[1]。

形式概念分析(FCA)是一种用来提取属性和对象二元关系的方法，形式概念分析在知识发现、信息检索和社会网络分析应用等领域中具有很高的应用价值，其中生成概念格能够很直观地显示数据[2]。处理大规模数据时，经典的概念格构造算法由于运行时间太长，在实际应用中不实用，概念格分布式构造算法能很好地解决这个问题。Wile提出了典型的分布式构造算法，包括叠置和并置两种[3]。Sokuznetso提出了基于闭包的概念格分布式构造算法[4]。BiaoXu等人提出了MapReduce架构下的MRGanter算法和MRGanter+算法，其中MRGanter+算法极大提高了并行算法的效率[5]。

在实际应用中，信息系统中常常会出现带有缺失的数据。文献[6]提出了不完备形式背景下的概念格定义，在不完备形式背景中，包含1，0和？三种值，其中1表示概念格中对象具有某个属性，0表示对象不具有某个属性，？表示对象是否具有某个属性未知。文献[7]对近似概念格进行了定义并提出了一种近似概念格的增量式构造算法。

完备形式背景下并行建格算法不适用于处理不完备形式背景下的概念格，串行算法在数据规模大的情况下运行效率较低。针对近似概念格的特点，本文中介绍了两种基于MapReduce框架的不完备形式背景下的并行构造方法：并行合并算法，增量式并行构造算法。

2 近似概念格基本概念

定义1[2]? K −(U, A, I )为一个形式背景，其中?U 为对象集；? A 为属性集；?I 为 ?U 和 ?A之间的二元关系；若 ?(x, a)?I， 则称x具有属性 ?a，用1表示，即?I( x ，a ) − "1"，若 ?(x,a)?I， 则称x不具有属性 ?a，用0表示，即

对于形式背景? (U, A, I) ，在对象集 ?X?U和属性集上分别定义运算? P (U) 与 ?P( A)上的一元运算：表示 ?X中所有对象共同具有的属性集合，表示具有 ?B中所有属性的对象集合。

定义2[2]设 ?(U, A, I) 是形式背景，令如果一个二元组? (X, B) 满足则称?(X, B)是一个形式概念。其中，X称为形式概念的外延，?B 称为形式概念的内涵。

定义3[6]在形式背景?(U, A, I) 中，若?I( x ，a ) − "1"表示对象 ?x 具有属性 ?a，?I"0"表示对象x不具有属性 ?a。在一些具有缺失值的信息系统中，用 ?I来表示对象? x是否具有属性?a 未知，称三元形式背景为不完备形式背景。

定义4[7]在一个不完备形式背景中，设，定义：为X中所有对象共同具有的属性集合，为X中所有对象可能共同具有的属性集合。

定义5[7]在一个不完备形式背景中。令和，两个运算和分别定义：

定义6[7]在一个不完备形式背景（U，A，｛1，？，0｝，I）中，?X ? 2U和 ?(B, C)− 2A? 2A，若 ?X −(B, C)，以及? (B, C)?X，称（X，（B，C））为形式背景（U，A，｛1，？，0｝，I）上的近似概念。近似概念（X，（B，C））的外延为X，（X，（B，C））的内涵为（B，C）。

3 用合并方法构造近似概念格的并行算法

3.1 算法基本思想

定义7[8]形式背景K1=（U1，A1，I）1和形式背景K2=（U2，A2，I）2，对于任意?12和任意满足 ?uI1a − uI2a，则称K1和K2是一致的，否则称K1和K2是不一致的。

定义8[8]如果形式背景K1=（U1，A1，I）1和K2=（U2，A2，I）2是一致的，那么它们的合并式：K1⊕K2=（U1∪U2，A1∪A2，I1∪I2），⊕称为K1和K2的加运算。如果A1=A2，称K1±K2=（U1∪U2，A，I1∪I2）是两个形式背景的纵向合并，如果U1=U2，称K1±K2=（U，A1∪A2，I1∪I2）是两个形式背景的横向合并。

不完备形式背景? (U, A, {1,?,0},I) 中，若? x?X, a ?A，?I( x ，a ) −"1"表示对象? x 具有属性? a，?I ? x, a ?−"0"表示对象? x 不具有属性? a。?I ( x ，a ) −"1"时，设K1=（U1，A1，I）1，?I ? x , a ?−"0"时，设K2=（U2，A2，I）2。则有:若A1=A2，称K1±K2=（U1∪U2，A，I1∪±I2）是两个形式背景的纵向合并，若U1=U2，称K1K2=（U，A1∪A2，I1∪I2）是两个形式背景的横向合并。

定理1[9]令U表示一个非空有限对象集，A表示一个非空有限属性集。定义映射：

定义9将不完备形式背景? (U, A, {1,?,0},I)的未知值“？”全部替换为“0”得到形式背景（U，A，I1），全部替换为“1”得到形式背景（U，A，I2）。通过两个完备形式背景的横向合并或纵向合并可以得到不完备形式背景? (U, A, {1,?,0},I)的全部近似概念（X，（B，C））。

证明：（X，C）是形式背景（U，A，I2）的概念，由映射LIN和HIN得到? X LIN( X ),?(B, C ) −HIN(B, C)，又由形式背景（U，A，I1）中的映射L1，H1和形式背景（U，A，I2）中的映射L2，H2满足定理2的（L）、（H）、（LH1）、（LH2），得出L（2X）=C，H（2C）=X，根据定理2，得出?X (L1( X),L2(X))，又由L（1X）=B，有X□=（L（1X），L（2X））＝（B，C）。同理由H2≤H1，得到（B，C）□=X，则（X，（B，C））是近似概念。由此可知，可以通过合并得到全部近似概念。

证毕。

若（X1，（B1，C1））和（X2，（B2，C2））是一个不完备形式背景? (U, A, {1,?,0},I)的两个近似概念，那么将不完备背景? (U, A, {1,?,0},I)中的未知值“？”全部替换为“0”得到形式背景（U，A，I1），将其中的未知值“？”全部替换为“1”得到形式背景（U，A，I2）。

设形式背景（U，A，I2）中的一个概念为（X2，B2），遍历（U，A，I1）中的所有概念，通过判断和（X2，B2）的关系来找到下一个概念。三个判断条件：

（1）若（U，A，I1）中找到概念（X1，B1）（其中（X1=X2），若B1=B2，则将概念（X1，（B1，B2））加入到近似概念格中。

（2）若（U，A，I1）中找到概念（X1，B1）（其中X1=X2），若B1≠B2，则将概念 ?(X1,(B1,?))加入到近似概念格中。

（3）若（U，A，I1）中没有找到概念（X1，B1）（其中X1=X2），则将概念? (X1,(−,B2))加入到近似概念格中。

定义10若（U，A，I2）中所有概念为（X1，B1），（X2，B2），（X3，B3）…（Xn，Bn）通过（Xn，Bn）遍历（U，A，I1）中的所有概念得到近似概念的集合为? {a ppron}，?{a ppro1}{ appro2} {a ppron}，可以得到不完备形式背景? (U, A, {1,?,0},I)的所有近似概念。

根据定义10，可以将近似概念格转化为n个子集的并集，说明了并行合并算法在MapReduce架构中实现是可行的。

3.2 算法描述

将不完备背景 ?(U, A, {1,?,0},I)中的未知值“？”全部替换为“0”得到完备形式背景（U，A，I1），将其中的未知值“？”全部替换为“1”得到完备形式背景（U，A，I2）。采用MRGanter+算法生成两个概念格[5,10-13]。由形式背景（U，A，I1）生成的概念格为概念格a,将概念格a输出在文件file1中；由形式背景（U，A，I2）生成的概念格为概念格b,将概念格b输出在文件file2中。

将输入文件设为file1,通过Map函数将概念格a中所有的概念都加入到哈希表concept1[14]，其中概念格a属性为哈希表的key,概念为哈希表的value，算法描述如下：

算法1 把概念格a加入到哈希表中

Map.把（U，A，I1）所有概念加入到哈希表concept1中Create Hashtable concept1//在Map函数之前建立哈希表Concept1

Input（:objects,concepts）.//输入完备概念格1的属性和概念

Output（:null）.//把结果加入哈希表，没有输出

1:concept.key←extension；//将概念的外延加入到哈希表

2:concept.value←intension;//将概念的内涵加入到哈希表

3:Return null;//Map函数输出为空值，把值加入到哈希表concept1中。

将输入文件设为file2，通过Map函数按行读取概念格b中的概念。通过哈希表concept1判断概念的外延是否存在于concept1中，如果不存在，就加入概念格b到近似概念格中；如果存在，判断内涵是否和概念格b相同，相同就把合并的概念格加入到近似概念格中，如果内涵不相同就把概念格1中的概念加入到近似概念格中。算法描述如下：

算法2 合并生成近似概念格

Map.把概念格进行合并

Input:（objects，concept2）//输入完备概念格2的对象和概念

Output:ApproConcept.//近似概念格外延为key,内涵为value

1:get object in concept1;//从哈希表concept1读取一个object，object即是extension

2:if extension is exist

3:if（concept2.Intension is equal to concept1.Intension）//如果外延相等

4:ApproConcept←（object，（concept1.Intension，concept2.Intension））；//进行合并

ENDIF

5:else

6:?ApproConcept ?（object,( c oncept1. I ntension,?));ENDELSE

7:else

8:?ApproConcept? (o bject, (−,c oncept2.Intension））；ENDIF

9:Return ApproConcept；

Reduce.输出所有Map中Key和Value

Input:（key，value）；//Map中Key和Value

Output（:key，value）；

1:context←（key，value）；

2:Return context；

4 一种增量式并行建格算法

4.1 算法基本思想

定理2[7]在一个不完备形式背景?(U, A, {1,?,0},I)中，令和其中Q和T是两个索引集。那么：

推论1[7]在一个不完备形式背景中那么?( X ,X )和（（B， C）□，（B，C）□□）是的两个近似概念。

证明：通过定理2和定义6可以得到推论1。

定理3[7]若是一个不完备形式背景，则偏序集在下确界? (?)和上确界 ?(?)作为一个完备格的近似概念分别为：

证明：通过推论1和定理2可以得出定理3。

近似概念格的结构特点与经典概念格的结构特点一致。在一种经典概念格构造算法的基础上[15]，文献[7]提出了一种近似概念格串行增量式算法。采用增量算法的特点是将插入的概念与已有的近似概念进行比较，满足条件就生成新的近似概念。在串行增量式算法基础上提出了一种增量式并行构造算法。

设 ??表示已生成的近似概念， 表示第1到第n个属性，第一个近似概念加入到 ??中，设 ?S??，?(X ,(B, C))为从S中取出的一个近似概念。

?Xi中 ?i 不为1时，设?S??，遍历S，（X，（B，C））为从S中取出的一个近似概念。判断条件如下：

（1） 若那么将（X∪xi，（B，C））加入到 ??中，并且将（x，（B，C））从??中移除。如果满足到步骤2，否则到步骤3。

定义11若在属性为xi中找到的近似概念集合为 ?approi,?{ appro1} {a ppro2}{ approi}可以得到不完备形式背景? (U, A, {1,?,0},I)所有的近似概念。

根据定义11，可以把近似概念格分为很多子集的并集，说明了将增量式算法在并行环境中运行是可行的。

4.2 算法描述

因为MapReduce架构是按行读取，求出每一个属性的上近似内涵和下近似内涵，并把属性的上近似内涵和下近似内涵放在一行。通过一次Map和Reduce生成所有近似概念。

算法5生成所有的近似概念。算法5中Map类生成每一行（即每个属性）的内涵，其中内涵包括上近似内涵和下近似内涵，每个属性的近似概念保存在一行之中，方便Reduce函数的计算[16]。在Reduce类之前，首先构造一个Hash表concept1。Reduce类中把第一次的近似概念加入concept1,然后生成一个list1，把concept1中的元素放入list1。遍历list1，进行判断，如果满足条件就插入新的元素。到了最后一个近似概念时，插入? {−,{U, U}}。

表1 函数的描述

算法3找到对象的下近似内涵

Input:(objecti,Xi).//Xi表示第i个属性,objecti表示第i个属性中所有的bool值

Output:DownIntensioni

1:if objectij=1 then

2:? DownO?j;//如果在第i个属性中第j个对象的boolean值为1，那么就将j的下标加入到DownO中

3:? OConcept −findOconcept? D ownO ?;//找到Downobject的内涵

4：?A Concept −findAConcep（t OConcept）； //找到OConcept的外延

5：?U PIntension −findOConcept? AConcept ?；//找 到AConcept的内涵

ENDIF

6:Return ?UPIntension//返回下近似内涵

算法4 找到对象的上近似内涵

Input: ?(o bjecti, Xi).// ?Xi表示第 i个属性, objecti表示第i个属性中所有bool值

Output:?UPIntensioni

1:if? objectij? 1?||?o bjectij= ?"?"then

2:? ?Downobject???j；//如果在第i个属性中第j个对象的boolean值为1或者为“？”，那么就将j的下标加入到Downobject中

3:?O Concept???f indOconcept? D ownobject?；//如果满足?((D ownIntensioni−B,U PIntensioni?C)?(D ownIntensio ni, UPIntension）i，则找到Downobject的内涵??

4:? AConcept?? findAConcep（t OConcept）；//找 到OConcept的外延

5:? UPIntension???f indOConcept? A Concept?.//找 到AConcept的内涵

6:Return ?UPIntension//返回上近似内涵

最后通过算法4生成所有的近似概念格，用Map函数生成所有概念的上近似和下近似，用Reduce函数生成所有的近似概念。

算法5 生成所有的近似概念（主程序）

Map.找到对象的上近似内涵和下近似内涵Input:?( o bjecti?,Xi).//?Xi表 示第i个属性, ?o bjecti表示第i个属性中所有bool值

Output:? (Xi,(?D ownIntensioni,? U PIntensioni)).

1:?D ownIntensioni???f indDownConcepti on(o bjecti); //findDownConception的函数实现在算法3

2:? UPIntensioni???findUpConception?(Xi);//findUpConception的函数实现在算法4

3:Return ?(Xi,?(D ownIntensioni,?U PIntensioni))；

Reduce.生成所有的近似概念

Create Hashtable ?concept1//在Reduce函数之前建立哈希表

Input: ?(Xi,?(D ownIntensioni,?U PIntensioni)).//输入Map函数输出的key和value

Output: ?concept1．//属性为key,概念的外延和内涵为value

1:foreach?concept1

2:if ?concept1is null then

3:? concept1??(Xi,?(D ownIntensioni,?U PIntensioni))；//遍历哈希表，如果为空就加入第一个元素

ENDIF

4: ?list1???c oncept1；//新建list类型list1，并赋值

5:foreach ?(B, C) in ?list1do //遍历list1

6:if? (DownIntensioniB,UPI nte niC) (,C)then

7:concept1 −X ?XiB, C

ENDIF

8:if?((D ownIntensioni,UPIntensioni) ??(DownIntensionj,UPIntensionj))(?j?i)then

9:?concept1 −(Xi,(DownIntensioni,UPIntensioni))

ENDIF

10:else

11:if?((DownIntensioni−B,UPIntensioni??C )?(DownIntensioni,（DownIntensioni，?UPIntensioni)(?j?i )then

12:?concept1 −(X?{Xi},(DownIntensioni??B,UPInte-nsioni?C B,UPIntensioni?C))

ENDIF

ENDELSE

13:if ?(D ownIntensioni,UPIntensioni)??(DownIntensionj,UPIntensionj)(?j?i) then

14:?concept1 −(Xi（,DownIntensioni, UPIntensioni))ENDIF

15:if ?Xiis lastthen

16:? concept1 −(?,(A,A))//如果是最后一个近似概念，将概念加入哈希表

ENDIF

17:return ?concept1

5 算法实验分析

5.1 数据集及实验环境描述

实验数据集 ElectricityLoadDiagrams20112014 Data Set（简称LD2011_2014）来自http://archive.ics. uci.edu/ml/datasets.html，数据集描述如表2所示。试验环境为Hadoop集群，该集群由1个主控制节点和10个计算节点组成。每个节点的硬件配置为Intel® Pentium® D CPU2.80GHz，2GB内存和150G硬盘。操作系统为 LinuxCentos 6.3，JDk为 Java 1.7.0_17，Eclipse采用32位的Linux版本eclipse-3.3.2。MapReduce框架基于Hadoop平台1.2.1版本，其他采用系统默认设置。

5.2 算法效果及验证

第一次试验从数据集LD2011_2014中选定对象数为15000，属性数为100，随机生成20%的缺失数据，将新数据集命名为LD1。从LD1中选取1000个对象，每次增加1000个对象，增加到10000个对象，一共10次，最后一次对象为15000个对象,其中选取属性数固定为100，试验结果如图1-2所示，其中并行算法运行的节点为10个。

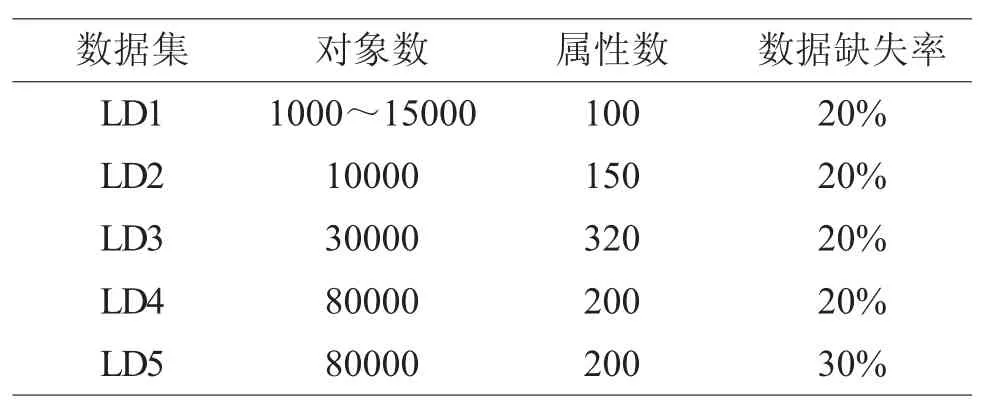
表2 数据集的描述

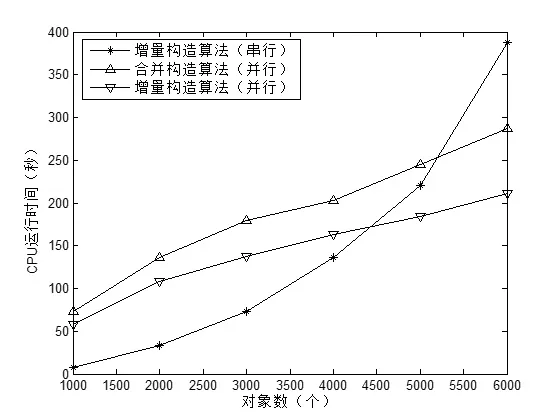
图1 对象数从1000到6000，属性数100，数据缺失率为20%时的试验结果

第二次试验从数据集LD2011_2014中选取10000个对象，150个属性，随机生成20%的缺失数据，将新数据集命名为LD2，分别运行得出在不同节点情况下两种并行算法的运行时间，试验结果如图3所示。

第三次试验从数据集 LD2011_2014中选取30000个对象，320个属性，随机生成20%的缺失数据，将新数据集命名为LD3，分别求出在不同节点情况下两种算法的运行时间。试验结果如表3所示。

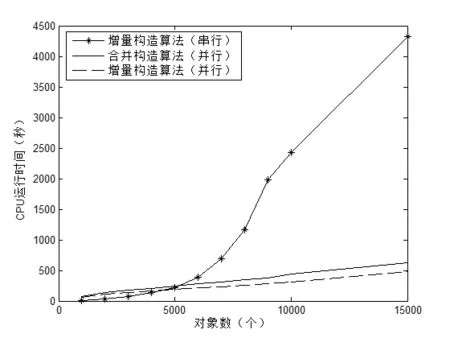
图2 对象数从1000到15000，属性数为100，数据缺失率为20%时的试验结果

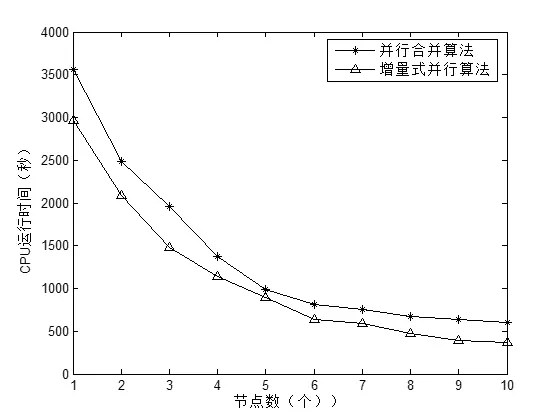
图3 节点数从1到10，对象数为10000，属性数为150，数据缺失率为20%时的试验结果

第四次试验从数据集LD2011_2014中选取80000个对象，200个属性，随机生成20%的缺失数据，将新的数据集命名为LD4，分别求出在不同节点情况下两种并行算法的运行时间。试验结果如表3所示。

第五次试验从数据集LD2011_2014中选取80000个对象，200个属性，随机生成30%的缺失数据，将新的数据集命名为LD5，分别求出在不同节点情况下两种并行算法的运行时间。试验结果如表3所示。

表3 并行算法运行时间(s)

如图1-2所示，对象数数据量较小时，串行算 法比并行算法运行更快，增量式并行算法与合并并行算法运行时间相差不大；当数据量具有一定规模时，并行算法的运行时间开始少于串行算法的运行时间，并且随着数据集的增大，差距越来越明显；随着数据集的增大，增量式并行算法运行时间相对合并算法差距增大。如表3所示，当数据集规模大时，随着节点数的增加，增量式并行算法的运行时间相比合并并行算法运行时间的优势更加明显。

对比表3中LD3和LD4数据集，虽然数据集LD4相对LD3对象数增加,但是属性数LD4相对LD3减少，导致数据集LD4的运行时间低于LD3的运行时间。

对比表3中LD4和LD5数据集。数据集LD4和LD5的对象数和属性数相同，但是数据集LD4和LD5的数据缺失率不同，导致LD5相对LD4的运行时间大幅度增加。

6 结束语

针对不完备形式背景，本文提出了MapReduce框架下的近似概念格并行合并算法和增量式并行算法。并行合并算法生成两个经典概念格后进行合并，增量式并行算法通过插入对象的内涵与已有的近似概念求交集和比较生成新的近似概念。试验结果表明，在数据规模较大时，并行算法相对串行算法大幅度减少了运行时间，计算节点越多并行算法相对串行算法的优势越明显。并行增量式算法比并行合并算法效率更高，数据规模越大，并行增量式算法优势越明显；节点越多，并行增量式算法优势越明显。并行合并算法相比增量式并行算法运行时间较慢。

构造近似概念格的下一步工作是不完备形式背景中知识的获取和决策分析，进一步将并行算法应用到这些工作中能够提高算法运行的效率。

[1]程广,王晓峰.基于MapReduce的并行关联规则增量更新算法[J].计算机工程,2016,42(2):21-25. Cheng Guang,Wang Xiaofeng.Incremental Updating Algorithmof Parallel Association Rule Based on MapReduce[J]．Computer Engineering,2016，42(2):21-25,32.

[2]Stumme G.Formal Concept Analysis[J].Electronic Notes in Discrete Mathematics,1999,2(3):199-200.

[3]Ganter B,Wille R.Formal concept analysis:mathematical foundations[M].Springer Science&Business Media,2012.

[4]Kuznetsov S O.Machine Learning on the Basis of Formal Concept Analysis[J].Automation&Remote Control,2001, 62(10):1543-1564.

[5]Xu B,Fréin R D,Robson E,et al.Distributed Formal Concept Analysis Algorithms Based on an Iterative MapReduce Framework[M].Formal Concept Analysis.Springer Berlin Heidelberg,2012:292-308.

[6]Wille R.RESTRUCTURING LATTICE THEORY:AN APPROACH BASED ON HIERARCHIES OF CONCEPTS[C]. International Conference on Formal Concept Analysis. Springer-Verlag,2009:445-470.

[7]Li J,Mei C,LvY.Incomplete decision contexts:Approximate concept construction,rule acquisition and knowledge reduction[J].International Journal of Approximate Reasoning, 2013,54(54):149-165.

[8]智慧来,智东杰,刘宗田.概念格合并原理与算法 [J].电子学报,2010,38(2):455-459. Zhi H L,Zhi D J,Liu Z T.Theory and Algorithm of Concept Lattice Union [J].Acta Electronica Sinica,2010,38(2): 455-459.

[9]张慧雯,刘文奇,李金海.不完备形式背景下近似概念格的公理化方法[J].计算机科学,2015,42(6):67-70. Zhang Huiwen,Liu Wenqi,Li Jinhai.Axiomatic Characterizations of Approximate Concept Lattices in Incomplete Contexts[J].Computer Science,2015,42(6):67-70.

[10]Ganter B.Two Basic Algorithms in Concept Analysis[C]. Formal Concept Analysis,International Conference,Icfca 2010,Agadir,Morocco,March 15-18,2010.Proceedings. 2010:312-340.

[11]Dean J,Ghemawat S.MapReduce:Simplified Data Processing on Large Clusters[J].In Proceedings of Operating Systems Design and Implementation(OSDI),2004,51(1): 107-113..

[12]Jin W,Wang C.Iteration MapReduce framework for evolution algorithm[J].Journal of Computer Applications,2013, 33(12):3591-3595.

[13]Rosen J,Polyzotis N,Borkar V,et al.Iterative MapReduce for Large Scale Machine Learning[J].Computer Science, 2013.

[14]Ruixia LI,Liu R,Zhou X.Optimization on MapReduce algorithm based on Hash table[J].Journal of Shandong University(Natural Science),2015,50(7):66-70.

[15]Godin R,Missaoui R,Alaoui H.INCREMENTAL CONCEPT FORMATION ALGORITHMS BASED ON GALOIS (CONCEPT)LATTICES[J].Computational Intelligence, 2010,11(2):246–267.

[16]Tonsmann G.Sequential and Parallel Rule Extraction from a Concept Lattice[C].International Conference on Data Mining,Dmin 2006,Las Vegas,Nevada,Usa,June.2006.

Parallel Constructing Algorithm of Approximation Concept Lattice Based on MapReduce Framework

Tan Fulin,Jiang Lin

（Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China）

Formal context with missing values is called incomplete context,and the concept lattice expansion model in incomplete context is called approximation concept lattice.In the approximation concept lattice construction,serial algorithm is low efficiency in the case of large data and parallel constructing algorithm under complete context is not appropriate for incomplete context.In order to solve these problems,through deep analysis of the characteristics of approximation concept lattice,the paper introduces two parallel constructing algorithms of approximation concept lattice based on MapReduce framework,including a parallel union algorithm and a parallel constructing algorithm based on an incremental constructing algorithm.The experimental results demonstrated that the two constructing algorithms had improved the efficiency of construction comparing with the serial algorithm.

Incomplete context；Approximation concept lattice；Construction of concept lattice；MapReduce framework；Parallel constructing algorithm

10.3969/j.issn.1002-2279.2017.02.011

TP301.6

A

1002-2279-（2017）02-0045-07

国家自然科学基金地区基金（KKGD201203003）;云南省教育厅重大项目（KKJI201203002）

谭富林（1992-），男，湖南省郴州市宜章县人，硕士研究生，主研方向：并行数据挖掘和机器学习。

姜麟（1969-），男，副教授，主研方向：智能计算和并行计算。

2016-10-09