基于小波包和RobustICA的无线电混合信号分离
杜太行, 王景玉, 江春冬, 郝 静,3
(1.河北工业大学控制科学与工程学院,天津 300130;2.河北省控制工程研究中心,天津 300130;3.石家庄信息工程职业学院计算机应用系,河北 石家庄 050000)
基于小波包和RobustICA的无线电混合信号分离
杜太行1,2, 王景玉1, 江春冬1,2, 郝 静1,3
(1.河北工业大学控制科学与工程学院,天津 300130;2.河北省控制工程研究中心,天津 300130;3.石家庄信息工程职业学院计算机应用系,河北 石家庄 050000)
针对复杂电磁环境下无线电混合信号分离困难的问题,提出将小波包和鲁棒性独立分量分析(RobustICA)算法应用于较低信噪比且频率接近的无线电混合信号的分离。首先用小波包分析方法对混合信号进行降噪预处理,然后采用盲源分离算法中的鲁棒性独立分量分析算法对降噪后的混合信号进行分离,通过观察分离后信号的波形和频率以及相似系数对分离结果进行定性和定量分析。所提算法与单独采用RobustICA算法的结果对比表明:所提算法分离出的信号在波形和频率以及相似系数方面均比单独采用RobustICA算法取得的效果好,从而证明所提算法可以较好地应用于无线电混合信号的分离。
小波包分析;盲源分离;鲁棒性独立分量分析;无线电混合信号
0 引 言
在复杂的电磁环境中,存在着大量与噪声混合在一起的多个无线电信号,其信噪比可能很低,或者信号间的频率很接近,导致用常规的方法很难将它们分离开来加以利用。
盲源分离(BSS)是信号处理中的一个传统而又富有挑战性的技术,它利用源信号之间的独立性将混合后的各源信号分开。独立分量分析(ICA)在处理相互独立的源信号混合成的信号时,可以认为与盲源分离是一致的。因而许多文献将盲源分离与ICA不加区分[1]。其中文献[2]和文献[3]分别使用FastICA在雷达快速扫描方面和谐波检测方面都取得良好的效果。文献[4]中将FastICA和RobustICA算法在盲源分离中的性能进行了分析,结果表明RobustICA算法在鲁棒性、收敛性以及计算复杂度方面的综合性能要优于FastICA算法。同时文献[5]采用RobustICA对复合故障信息进行分离,也达到了良好的分离效果。文献[6]和[7]均采用盲源分离的方法分别将认知无线电网络中的宽频谱信号和频谱混叠无线电混合信号进行分离,而将RobustICA算法应用于无线电混合信号分离的研究却鲜有。又由于目前采用盲源分离方法对无线电混合信号进行分离大部分是用盲源分离方法中的FastICA,而RobustICA算法比FastICA算法的综合性能好[4],所以考虑使用RobustICA算法对无线电混合信号进行分离,然而单独使用RobustICA算法分离混合信号,当信噪比较高时,可以较好地将混合信号分离,但当信噪比较低时,分离的效果并不理想,这时可以考虑在使用RobustICA算法前用一定的方法对混合信号进行去噪,然后再进行分离。文献[8]提出采用小波包和独立分量分析对多源声发射信号进行分离,较好的提取出裂纹、摩擦等故障源信号。
本文针对信噪比较低的无线电混合信号分离问题,考虑将小波包分析引入到RobustICA算法中。首先采用小波包分析对较低信噪比的无线电混合信号进行降噪预处理,然后利用RobustICA算法对降噪后的混合信号的分离,以期取得良好的分离效果。
1 小波包分析原理
小波包分析是在小波分析的基础上延伸与发展而来,它是一种更加精细的分析方法,可以同时对信号的低频和高频进行多层次的划分,而小波分析并没有对信号的高频部分进一步分解,从而使得小波包分析提高了信号的频率分辨率。
在小波包分析中[9],定义子空间 Unj是函数 un(t)的闭包空间,U2nj是函数u2n(t)的闭包空间,并存在以下双尺度方程:
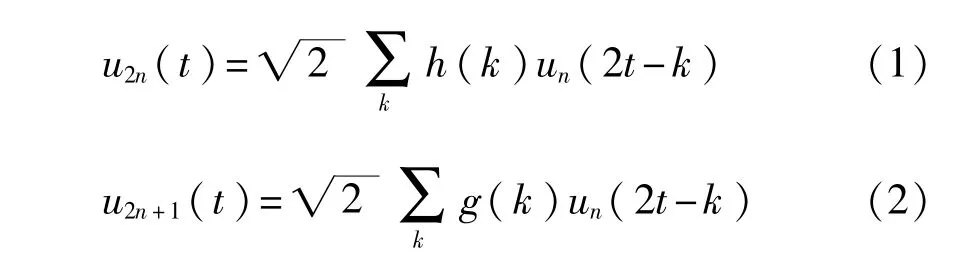
其中 n 表示函数序号,n∈Z+,{h(k)}k∈Z和{g(k)}k∈Z是一组共轭镜像滤波器的低通、高通表示,g(k)=(-1)kh(1-k),函数族{un}为小波包。
式(1)和式(2)在本质上反映了函数空间的以下关系:
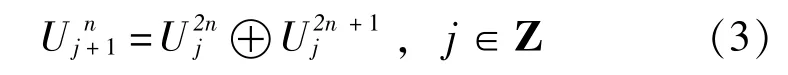
小波包分解和重构的公式[10]如下:
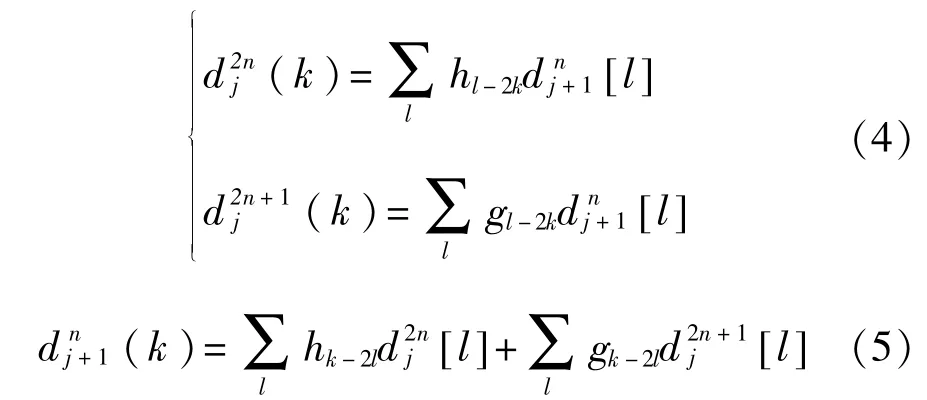
其中d2nj和d2n+1j分别为尺度2l下的一个逼近函数在子空间U2nj和U2n+1j上的投影。
根据小波包分析原理,利用小波包分析对含噪信号的降噪预处理步骤包括:
1)对含噪信号进行小波包分解,选择小波基为db13,分解层数为 5[11]。
2)对小波包分解得到的系数进行阈值量化,采用软阈值处理,保留低频系数。
3)对处理后的信号进行小波包重构,根据最低层的小波包分解系数和量化处理后的系数,进行小波包重构。
2 RobustICA算法原理
RobustICA算法是一种独立分量分析的算法,其原理建立在基本独立分量分析算法的基础上。
2.1 独立分量分析的模型
独立分量分析的实质是在源信号s(t)和混合矩阵A都为未知的情况下,根据已知的观测数据(在实际中,观测到的数据都会有噪声,假设噪声是以加性白噪声形式存在的):
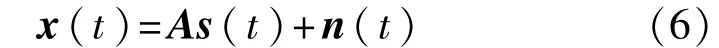
利用信号的统计特性确定分离矩阵W,使得:

其中 y(t)是 s(t)的复制或估计,s(t)=[s1(t),s2(t),…,sM(t)]T是M维信号向量,代表混合的信号个数为M个,x(t)=[x1(t),x2(t),…,xN(t)]T是 N 维观测向量,代表传感器个数为 N 个,n(t)=[n1(t),n2(t),…,nN(t)]T是噪声向量,A是N×M维混合矩阵,W是M×N维分离矩阵。独立分量分析模型框图如图1所示。
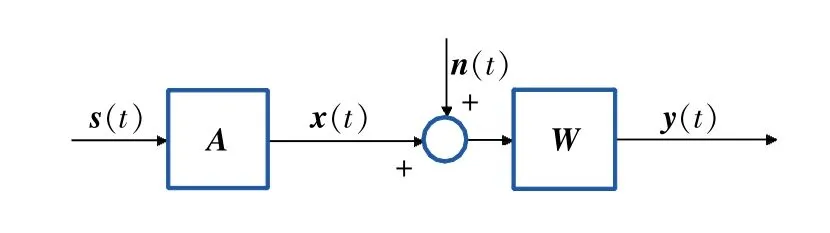
图1 独立分量分析模型框图
2.2 独立分量分析的约束条件和不确定因素
如果没有任何限定条件,那么独立分量分析是无明确意义的解,为了使独立分量分析问题可解,需要对源信号和混合矩阵做一些假设,即为独立分量分析的约束条件:
1)源信号所含各分量之间相互统计独立;
2)源信号中最多有一个信号是高斯信号;
3)混合矩阵A列满秩。
在实际情况中,约束1)的假设条件通常能满足;约束2)是因为多个高斯信号混合后仍是高斯信号,所以当混合信号中高斯信号多于一个时,各源信号不可分;约束3)的实际意义是采集信号的传感器数目必须不少于源信号的数目。
独立分量分析的不确定因素[12]包括分离后信号顺序排列和复振幅的不确定性,但波形保持不变。这是由于混合矩阵A和源信号s(t)都是未知的,从而使独立分量分析存在这两种不确定性和模糊性,但在实际应用中关心的不是信号的排列顺序和幅度,而是信号的波形和频率,所以独立分量分析存在的不确定因素并不影响实际的应用。
2.3 RobustICA算法
RobustICA算法是由Zarzoso等[13-14]提出的一种基于峭度和最优步长的独立分量分析算法。RobustICA的理论基础是数值优化领域中的精确线性搜索。然而传统的线性搜索只能在搜索方向达到局部最优化。RobustICA中采用的线性搜索方法能保证在每个分量的分离过程中达到最优,通过代数计算全局优化步长,沿搜索方向实现峭度的最优化。
假设有噪观测混合数据为x,这里不必对其进行白化处理,仅要求其均值为零,分离后的数据为y,其峭度公式为
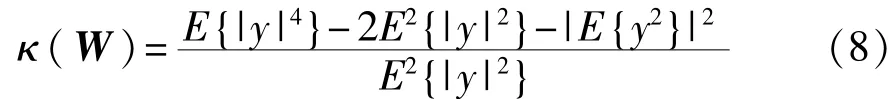
在没有简化假设条件的情况下,使用峭度绝对值目标函数的精确最佳线性优化步长搜索,表达式如下:
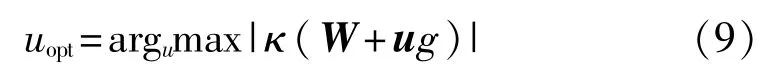
方向为搜索梯度g的方向,其中g=▽Wκ(W),可以由式(6)得出。

式中:κ(W)——统计量;
E(…)——数学期望;
y——解混后的数据;
u——优化步长。
综上可得RobustICA执行全局最佳步长的优化的迭代步骤为:
1)计算最优步长多项式系数,对于峭度目标函数,最优步长多项式由下式给出:
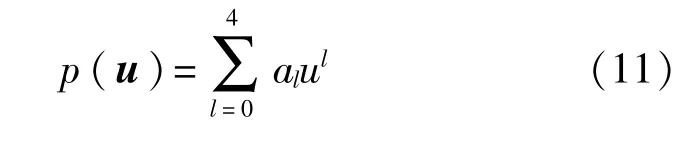
其中系数{al}4l=0在每次迭代中通过观测信号和W与g的当前值获得。
2)求出最优步长多项式的根{ul}4l=0。
3)选择多项式的根,使得沿搜索方向目标函数的绝对值最大:
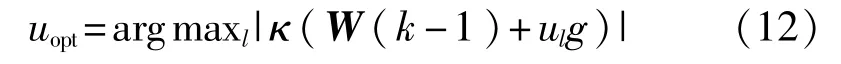
4)更新:
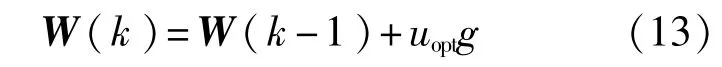
5)归一化:

3 分离信号的评价指标
为了评价算法的分离性能,可以从定性分析和定量分析两方面进行。在定性分析方面,可以观察分离出信号的波形和频率,将其作为分离信号的评价指标。在定量分析方面,由于独立分量分析方法中存在复振幅的不确定性,而相似系数具有归一化的特点,因此为了避免这种不确定性,用相似系数作为评价指标,说明算法的分离性能。相似系数的计算公式如下:
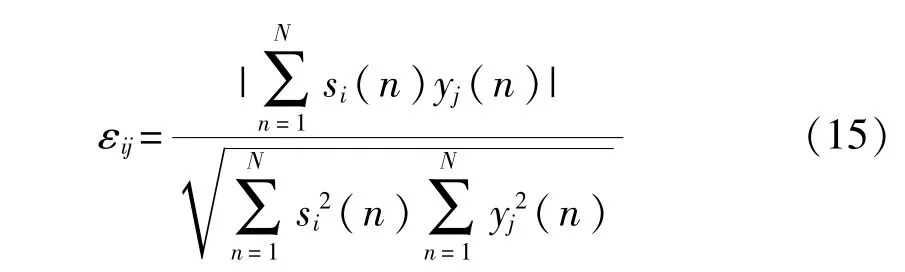
式中:si(n)——源无线电信号;
yj(n)——经过RobustICA分离后的信号。
又由于独立分量分析存在分离出信号的排列顺序不确定,为了实现自适应识别分离信号与相应的源信号进行运算,得到相应的相似系数,将分离出的每个信号均与各个源信号进行相关系数运算,因此就构成了相似系数矩阵。因而由εij构成的相似系数矩阵R每行每列有且仅有一个元素接近1,其他元素接近0,则认为无线电源信号得到分离。因为相似系数接近1的程度越高,分离出的信号与相应的源信号越接近,则说明分离的效果越好。
4 仿真研究
利用Matlab仿真软件,采用3个无线电混合信号进行分离研究。首先对无线电混合信号单独使用RobustICA算法进行仿真研究,然后再对无线电混合信号使用本文所提算法进行仿真研究,最后对这两种算法的实验结果进行对比分析。
3个源无线电信号频率分别为5,8,10Hz。混合矩阵A是由rand()函数产生的随机矩阵。所采用的模型是按式(6)进行混合,由于算法要求混合矩阵列满秩,因此假设A为3×3维混合矩阵。其中3个无线电混合信号的时域图和相应的频域图如图2所示。
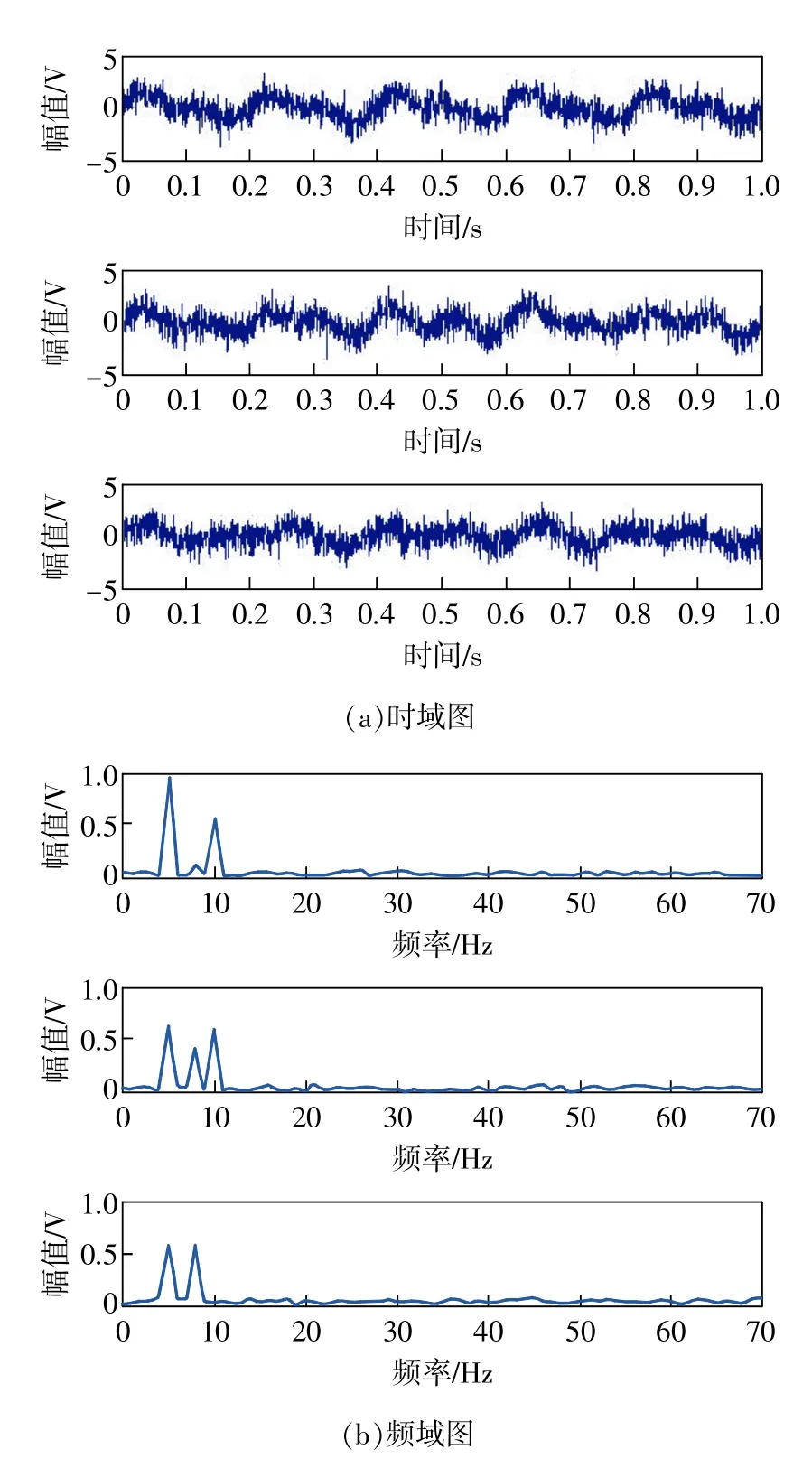
图2 无线电混合信号的时域图和频域图
4.1 单独采用RobustICA算法对混合信号的分离
本节单独采用RobustICA算法将信号进行分离,分离后的时域图和相应的频域图如图3所示。
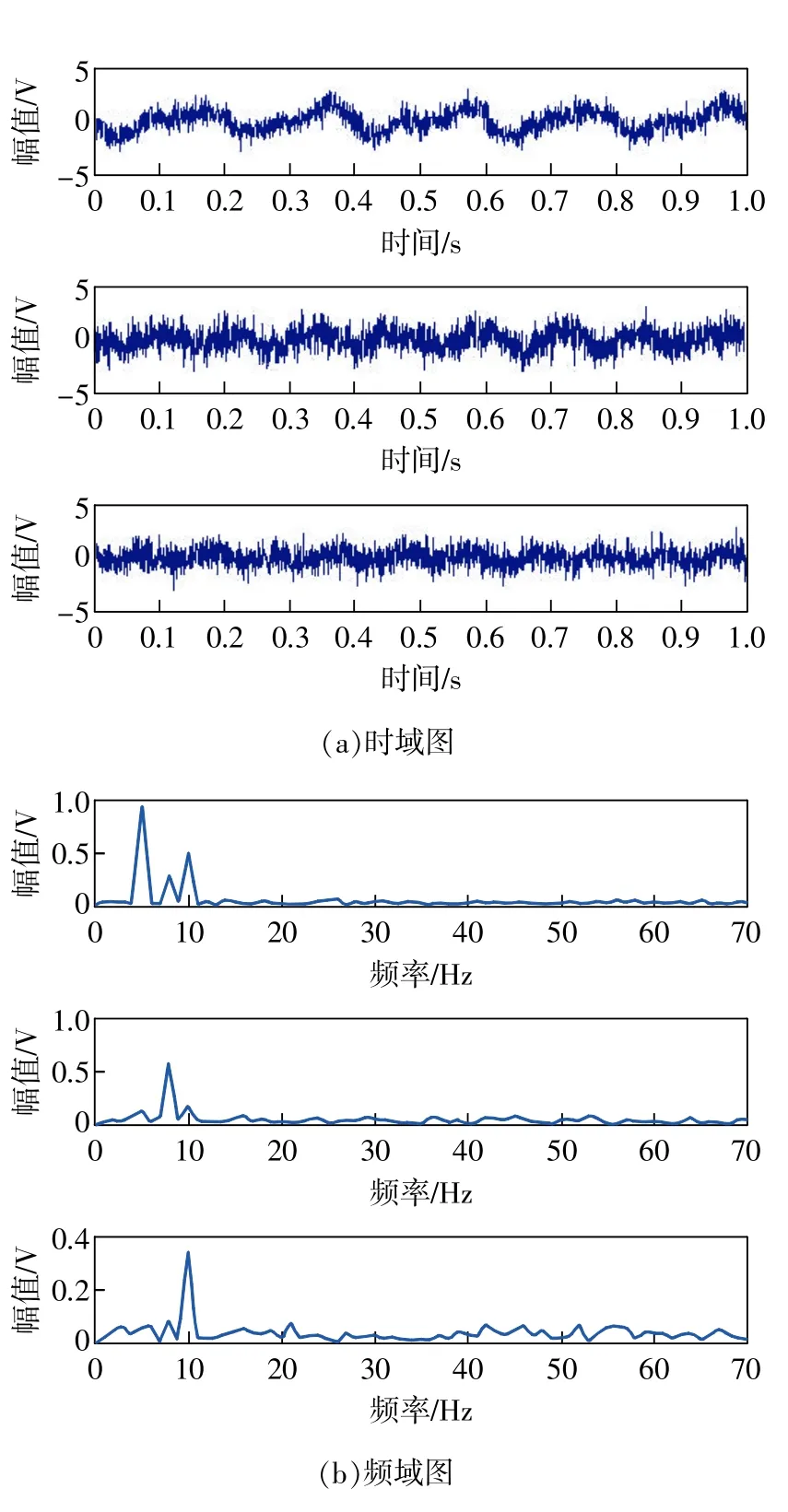
图3 RobustICA分离后的时域图和频域图
仿真实验中得到的相似系数矩阵为

由以上仿真结果可以得出,单独使用RobustICA算法在较低信噪比的情况下,不论是在时域分离出信号的波形,还是在频域中检测出信号的频率以及得到的相似系数都与源无线电信号相差较大。
4.2 小波包和RobustICA算法对混合信号的分离
本节采用小波包和RobustICA算法结合对信号进行分离,即首先采用小波包对混合信号进行降噪预处理后,再使用RobustICA算法对降噪后的混合信号分离,分离后的时域图和相应的频域图如图4所示。
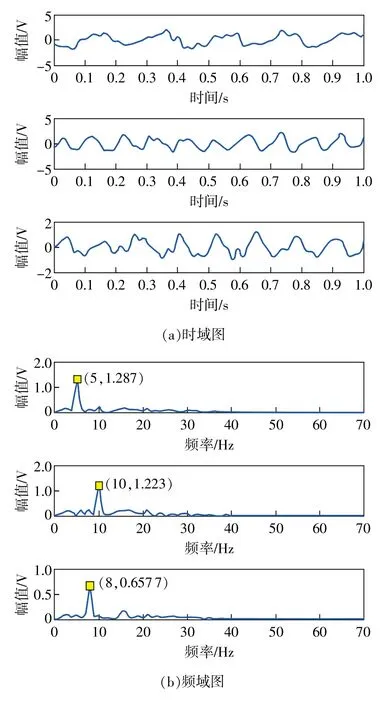
图4 所提算法分离后的时域图和频域图
仿真实验中得到的相似系数矩阵为

由仿真结果可以得出,在较低信噪比的情况下,经过小波包预处理降噪后,再使用RobustICA算法对降噪后的混合信号进行分离,不仅能够较好的分离出信号的大致波形和频率,而且相似系数矩阵中的相似系数总体接近于1。
仿真结果对比表明,在信噪比较低时,本文所提算法比单独使用RobustICA算法的分离效果好,从而证明所提算法的有效性。
5 结束语
本文将小波包和鲁棒性独立分量分析(RobustICA)算法结合应用于较低信噪比且频率接近的无线电混合信号的分离,通过对单独采用RobustICA算法和所提算法的对比,结果表明所提算法从波形和频率以及相似系数等方面对混合信号均取得了良好的分离效果,并且所提算法对复杂电磁环境下的无线电混合信号的分离提供了理论基础。同时,本文所采用的独立分量模型是在混合矩阵列满秩的情况下,当实际采集到的信号个数小于源信号个数的情况下还需要进一步研究。
[1] 郑辉.通信中盲信号处理理论与技术[M].北京:国防工业出版社,2013:435-462.
[2] 孟秋池,张子良,刘国庆.FastICA算法在雷达快速扫描中的应用[J].现代雷达,2012,34(2):41-45.
[3] 汪斌,王年,蒋云志,等.改进FastICA算法在谐波检测中的应用[J].电力自动化设备,2011,31(3):135-138.
[4] 吴微,彭华,张帆.FastICA和RobustICA算法在盲源分离中的性能分析[J].计算机应用研究,2014,31(1):95-119.
[5]姜万录,赫金娜,张生.基于盲源分离的液压泵复合故障诊断[J].液压与气动,2014(7):22-30.
[6]吕守涛,刘健.认知无线电网络中宽频谱的信号分离算法[J].计算机工程与应用,2013,49(7):11-15.
[7]杨保平,陈永光,谢桂武.频谱混叠无线电信号盲侦察识别技术[J].系统仿真学报,2014,26(8):1793-1806.
[8]王向红,尹东,胡宏伟,等.基于小波包和独立分量分析的微弱多源故障声发射信号分离[J].上海交通大学学报,2016,50(5):757-763.
[9] 史洁玉.Matlab信号处理超级学习手册[M].北京:人民邮电出版社,2014:311-334.
[10]高科,刘剑,刘玉姣,等.受限空间瓦斯爆炸冲击波压力信号小波包去噪研究[J].中国安全生产科学技术,2014,10(12):17-22.
[11]李月琴,栗平,闫晓鹏,等.无线电引信信号去噪的最优小波基选择[J].北京理工大学学报,2008,28(8):723-726.
[12]许士敏,陈鹏举.基于阵列天线的无线电侦查信号盲分离[J].电讯技术,2004(3):71-74.
[13]VICENTE Z,PIERRE C.Robust independent component analysis for blind source separation and extraction with application in electrocardiography[C]//Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society.NewYork:Engineering in Medicine and Biology Society,2008:3344-3347.
[14]VICENTE Z,PIERRE C.Robust independent component analysis by iterative maximization of the kurtosis contrast with algebraic optimal step size[J].IEEE Transactions on Neural Networks,2010,21(2):248-261.
(编辑:刘杨)
Separation of mixed radio signals based on wavelet packet and RobustICA
DU Taihang1,2, WANG Jingyu1, JIANG Chundong1,2, HAO Jing1,3
(1.School of Control Science and Engineering,Hebei University of Technology,Tianjin 300130,China;2.Control Engineering Research Center of Hebei,Tianjin 300130,China;3.Department of Computer Application,Shijiazhuang Information Engineering Vocational College,Shijiazhuang 050000,China)
Aiming at the difficulty of separating mixed radio signals in the complex electromagnetic environment, the wavelet packetand the robust independentcomponent analysis(RobustICA)algorithm is proposed for the separation of mixed radio signals with lower SNR and adjacent frequency.Firstly,wavelet packet analysis is used for the noise reduction pre-processing of the mixed signals.Then, the RobustICA algorithm based on blind source separation (BSS) algorithm is used to separate the mixed signals after noise reduction.And the results are qualitatively and quantitatively analyzed by observing the waveform and frequency of the signal and the similarity coefficient.The comparison of results obtained with the proposed algorithm and the application of independent RobustICA algorithm show that the proposed algorithm has better performance than the independent RobustICA algorithm in terms of waveform,frequency and similarity coefficient.And it is proved that the proposed algorithm can be applied to the separation of mixed signals well.
wavelet packet analysis; blind source separation; RobustICA; mixed radio signal
A
1674-5124(2017)06-0088-05
10.11857/j.issn.1674-5124.2017.06.019
2017-01-28;
2017-02-13
河北省自然科学基金资助项目(F2014202264)
杜太行(1963-),男,天津市人,教授,博士,研究方向为电器检测、计算机应用。

