一种改进的A-KAZE算法在图像配准中的应用

吴含前 李程超 谢 珏

(1东南大学计算机科学与工程学院, 南京 210018)(2东南大学计算机网络和信息集成教育部重点实验室, 南京 210018)(3东南大学蒙纳士大学苏州联合研究生院, 苏州 215123)

一种改进的A-KAZE算法在图像配准中的应用

吴含前1,2李程超1,2谢 珏3

(1东南大学计算机科学与工程学院, 南京 210018)(2东南大学计算机网络和信息集成教育部重点实验室, 南京 210018)(3东南大学蒙纳士大学苏州联合研究生院, 苏州 215123)

针对现有图像配准过程中难以保持图像的局部精度和边缘细节的问题,在A-KAZE算法的基础上提出了一种改进的图像特征提取算法AKAZE-ILDB.该算法首先利用非线性扩散滤波方程构造图像金字塔,采用快速显示扩散(FED)求得数值解,得到具有亚像素精度的图像特征点坐标；然后利用改进的LDB(ILDB)描述子构造具有尺度和旋转不变性的图像特征向量,对特征向量采用汉明距离进行KNN匹配；最后基于仿射变换模型计算空间映射参数矩阵来实现图像配准.实验结果表明:在保持相同图像特征匹配正确率的情况下, AKAZE-ILDB算法比A-KAZE算法平均配准时间缩短了300 ms; 在配准精度方面,比A-KAZE算法提高了3.7%,比传统特征提取算法SURF匹配正确率提高了29%.

A-KAZE; 非线性扩散滤波; FED; KNN匹配; 仿射变换

图像配准是将同一场景在不同时间、不同视角或者是不同传感器拍摄的2幅或多幅具有重叠区域的图像进行处理的过程[1].图像配准技术在计算机视觉、遥感技术、医学图像处理、图像融合、图像超分辨率重建等领域有着广泛的应用[2],特别是作为视频超分辨率领域的基础研究,一直是近年来的研究热点[3].

图像配准方法主要有3种:基于灰度信息的方法、基于变换域的方法和基于特征的方法[4].基于灰度信息的方法对异源图像配准效果较好,但是计算量大,要求图像有较大的重叠区域,容易出现局部极值.基于变换域的方法是采用频域的方法,利用傅里叶变换,通过对比、平移、旋转、缩放在时域和频域的对应关系,求得变换关系.而基于特征的图像配准方法是目前最常用的方法,因为这种方法只需要针对图像特征进行分析,减少了图像处理过程的运算量,并且对于亮度变化、图像变形和遮挡都有较好的适应能力.

传统的图像特征提取算法,如SIFT[5]，SURF[6]等都是基于线性的高斯金字塔进行多尺度分解来消除噪声和提取图像特征点.但高斯分解牺牲了局部精度作为代价,容易造成边界模糊和细节丢失.非线性的尺度分解可以解决这个问题,但非线性扩散方程并没有解析解,只能使用数值分析的方法来求解.传统的基于正向欧拉的方法求解时迭代收敛的步长太短、耗时长、计算复杂度高. KAZE算法[7]中采用加性算子分裂算法(AOS)来求解非线性扩散方程,可以采用任意步长来构造稳定的非线性尺度空间,但实现复杂.加速版本的KAZE算法(A-KAZE)采用快速显示扩散(FED)[8]数值分析框架来求解非线性扩散滤波方程,相比AOS算法在精度方面得到了较好的提升,并且降低了实现的复杂度.

但A-KAZE算法采用的M-SURF特征描述子构建的特征向量在进行特征匹配过程中耗时长且匹配精度不够高.针对这一问题,本文采用了一种改进的LDB(ILDB)特征描述子构建图像特征向量,使用汉明距离度量特征向量之间的相似度,提高匹配效率,并加入方向信息,增强了特征描述向量的鲁棒性.

综上所述,本文图像配准模型首先基于A-KAZE进行图像特征的提取与位置检测,然后利用ILDB描述子进行特征描述;接着根据汉明距离进行特征的相似性度量;最后计算变换矩阵,完成图像配准.

1 A-KAZE特征提取算法

A-KAZE算法[9]提取图像特征主要包括3个步骤:

1) 利用非线性扩散滤波方法和快速显示扩散(FED)求解隐性差分方程的原理来构建非线性尺度空间.

2) 检测感兴趣的特征点,这些特征点在非线性尺度空间上,是经过尺度归一化之后的Hessian矩阵行列式值在局部(3×3像素邻域)的极大值．

3) 构造特征向量,计算特征点的主方向,并基于一阶微分图像提取具有尺度和旋转不变性的特征描述向量.

1.1 构造非线性尺度空间

非线性扩散滤波是一种用流动函数的散度来描述图像亮度在不同尺度空间变化的方法,其可用以下非线性偏微分方程来描述:

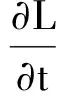
(1)

函数c定义如下:

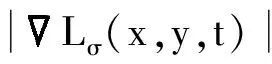
(2)

式中,函数g的定义可以根据不同的要求进行设计.本次实验中为了优先保留宽度较大的区域,将g定义为

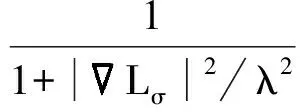
(3)

本文采用FED来求解方程(1)是因为它结合了显示和半隐式的优点. 另外，采用盒子滤波来近似高斯内核[10],降低了积分图的计算复杂度. FED的主要思想是进行M次循环,M为图像金字塔中组数O与层数S的积,即得到的滤波后的图像总数.每次循环都是一个n次的迭代过程,第j次迭代步长τj的定义为

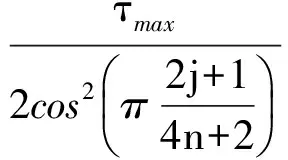
(4)

式中,τmax为不破坏迭代过程稳定性的最大迭代步长.利用显示扩散可以将偏微分方程(1)表示为显示模式:

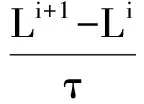
(5)

式中,τ为一个常量的迭代步长;A(Li)为图像的传导矩阵.进行迭代之后求解出的图像亮度表示为

Li+1,j+1=(I+τjA(Li))Li+1,jj=0,1,…,n-1

(6)

式中,I为单位阵;Li+1,0=Li为初始化的先验信息.

每一次迭代的时间由高斯滤波参数标准差σi决定.对每一层图像进行高斯滤波,滤波参数的值定义为

σi(o,s)=2o+s/S

o∈[0,O-1],s∈[0,S-1],i∈[0,M]

(7)

在传导扩散方程中以时间单元进行迭代,因此需要将空间滤波参数转化为时间单元.在高斯尺度空间下,使用标准差为σ的高斯核对图像进行卷积,相当于对图像进行持续时间为t=σ2/2的滤波.因此,尺度参数σi转化为时间单元的映射公式为

(8)

当结束某一层(oi)的滤波之后,在图像金字塔的下一层进行降采样操作,然后修改对比度因子λ，这样就可得到一个O组(每组S层)的图像金字塔.

1.2 特征点检测

特征点检测与SIFT算法类似.使用非极大值抑制方法,计算图像金字塔中每个像素点的Hessian矩阵,为了加快搜索速度,窗口大小固定为3×3像素.即在上一层和下一层以及周围共26个像素点中寻找归一化后不同尺度的Hessian矩阵行列式的局部极大值. Hessian矩阵行列式的值计算公式如下:

(9)

式中,σ为这一层的尺度参数σi的整数值;Lxx,Lyy分别为图像水平和垂直方向的二阶偏导;Lxy为交叉偏导数.

找到特征点后,利用空间尺度的泰勒展开式来求解特征点坐标:

(10)

式中,L(x)为图像亮度的空间尺度函数;x为特征点所在的坐标，其亚像素坐标的解为

(11)

1.3 ILDB特征描述子

LDB描述子是一种二值描述子[11],相比于传统的数值描述子SIFT,M-SUFR等,具有计算量小、实时性强的优点.判断一个描述子是否具备良好的特性,主要基于3个方面:

1) 差异性,即对于不同的特征具有强区分度;

2) 低计算复杂度,易于计算,匹配时消耗时间少,具有实时性;

3) 鲁棒性,对于光照变化、旋转等具有不变性.

LDB描述子不仅利用图像的灰度信息,而且引入了图像的一阶梯度信息, 因此具有很高的差异性.如图1所示,如果仅仅考虑平均灰度信息,那么3个图像的平均灰度是相同的. LDB使用2个网格内的平均灰度以及水平和垂直方向的一阶梯度信息来区分3个图像块.

图1 3个不同灰度分布的图像块

加入梯度信息虽然使描述子差异性增强,但没有加入方向信息和尺度信息会导致其对于图像的旋转和尺度变化比较敏感,降低了鲁棒性.针对这个问题,本文对LDB描述子进行改进,在LDB描述子构建之前加入主方向信息形成ILDB描述子.

使用灰度矩来描述主方向,图像块的灰度矩定义为

(12)

式中,(x,y)为像素点的坐标;p,q为常数，分别取0和1;I(x,y)为像素点灰度.利用灰度矩将图像的重心定义为

(13)

(14)

通过以上方法获得描述子的主方向.在对描述子进行构建时,首先将特征点的邻域图像块旋转到主方向,然后使用LDB描述子构造方法[11]构建最终的ILDB描述子.

2 特征向量匹配与变换矩阵估计

首先根据汉明距离对图像特征点的描述子进行匹配,然后使用随机一致性算法(RANSAC)进行误匹配点的删除．得到匹配对后,基于仿射变换模型求解图像之间的空间变换参数.

2.1 特征向量匹配及去误

在对特征点进行匹配时,首先需要度量2个描述子之间的相似度,本文采用汉明距离进行度量.汉明距离定义为2个向量中对应位置不同分量的个数.所以计算2个ILDB二值描述子之间的汉明距离非常简单高效,加速了图像特征的匹配速度.

在查找最佳匹配点时,采用KNN算法,其中K值取为2.这样对于每个特征点都有2个待匹配点,如果2个匹配对之间的距离比值足够大,说明最近邻是最优,否则存在不易区分的2个特征向量.将2个距离记为D1和D2,其中前者为最近邻距离,后者为次近邻距离.如果两者比值小于某个阈值,则接受这个最近邻的匹配点.实验表明,阈值在0.65～0.80之间为最佳.

上述操作虽然有助于找到一些最佳匹配点,去除一些不必要的匹配对,但在匹配结果中仍然会含有误匹配对.因此,在实验中再次采用RANSAC算法来拟合出最优的匹配对,去除误匹配对.

2.2 六参数仿射变换

得到匹配对后,将参考图像标定在待配准图像中,这样可比较直观地来判断配准效果.其中像素点坐标的变换,本文采用具有描述平移、旋转、缩放功能的仿射变换模型来实现.

在实际应用中,六参数变换模型是一种常用的坐标变换模型.设六参数变换的6个参数为m0～m5，则该模型可表示为

(15)

式中,(x,y)和(x′,y′)分别为参考图像和待配准图像匹配对中的像素点坐标;M为空间变换矩阵.从式(15)中可看出，求解6个参数的估计值至少需要3对匹配点.

在实际中, 匹配对往往大于3对,可采用最小二乘法来求得最佳的变换矩阵参数.

3 实验与结果分析

本文分别使用SURF,M-SURF以及ILDB三种描述子构建图像特征向量,这3种描述子对应的实验算法分别是SURF,A-KAZE和AKAZE-ILDB. 选择配准正确率和配准时间2个指标对算法进行评价分析.实验平台为Windows 7系统,CPU为Intel i5-3230M 2.6 GHz,8 GB内存的个人电脑.编程环境为Qt4.7和Opencv 3.1,所有代码都是单线程执行.实验采用KATHOLIEKE大学公开的4组图像进行测试[12],每组4幅图像,其中1幅作为参考图像,其余3幅作为待配准图像. 根据图片的现实场景,每组图像分别属于4种类别:

1) 不同视点,图像组命名为Graf;

2) 不同亮度,图像组命名为Leuven;

3) 不同模糊,图像组命名为Btree;

4) 压缩失真,图像组命名为Compa.

每组图像中的每一对图像1-2,1-3,1-4的配准难度逐渐上升,即待配准图像和参考图像的差异会越来越大.图2为每组图像中配准难度适中的图像对,编号为1-3.其中,图2(a)、(b)为不同视点的图像,它展现了图像的扭曲和旋转,而图2(g)、(h)为压缩失真的图像,其中出现了锯齿.

实验过程中,首先从配准时间的角度分析3种

(a) Graf1

(b) Graf3

(c) Leuven1

(d) Leuven3

(e) Btree1

(f) Btree3

(g) Compa1

(h) Compa3

算法的效率;其次从图像特征向量匹配正确率的角度分析3种算法所提取特征点的精确度.

算法时间上的开销主要包括3部分:① 非线性尺度空间的构造;② 特征描述向量的构造;③ 特征向量的匹配.

假设图像特征向量长度为n,则在匹配阶段采用的ILDB描述子进行匹配的时间复杂度为线性复杂度O(n).为了保证实验的一致性,3种算法采用的都是KNN匹配,其中K值为2.获取最佳匹配点的阈值设置为0.8,即最近距离与次近距离的比值需要小于0.8.取每组图像3次匹配的平均时间作为最终结果,如表1所示.

表1 3种算法针对每组图像的平均配准时间 ms

从表1中可看出,AKAZE-ILDB算法与原始的A-KAZE算法相比,在亮度变化的图像组(Leuven)中配准时间持平,但在其他组中具有明显的优势,总体来说平均配准时间减少了约300 ms. AKAZE-ILDB算法与SURF算法对比,虽然SURF算法在时间上具有优势,但在匹配正确率的实验中表现并不理想.

匹配正确率是算法检测出的特征向量中正确的特征向量所占的比例.设算法中检测出的特征向量数为N,正确特征向量数为C,则匹配正确率R计算公式为

R=C/N

使用已知的单应性矩阵检验实验算法计算出的特征向量是否为正确特征向量.在衡量2个特征向量是否相同的实验中[13],采用欧式距离度量2个特征向量之间的距离,在允许微小误差的情况下,会设置一个阈值,若两者之间的距离小于该阈值,则将算法检测出的特征向量记为正确特征向量.本实验所有算法的阈值设置为单精度浮点值2.5.

实验统计数据如图3所示.3种算法分别采用不同的直方格表示.每幅直方图表示一组图像的匹配正确率对比结果.

匹配正确率越高,表示算法提取出的特征点精确度越高.从图3中可看出,本文算法在图像亮度变换、不同模糊程度以及压缩失真的图像匹配中较另外2种算法有明显优势.这是因为AKAZE-ILDB利用非线性尺度空间构造图像金字塔来保持图像局部精度和边缘细节,因此在配准精度上保持了A-KAZE算法的优势.本文算法与A-KAZE和SURF算法相比，匹配正确率分别提高了3.7%和29%.

(a) Graf组

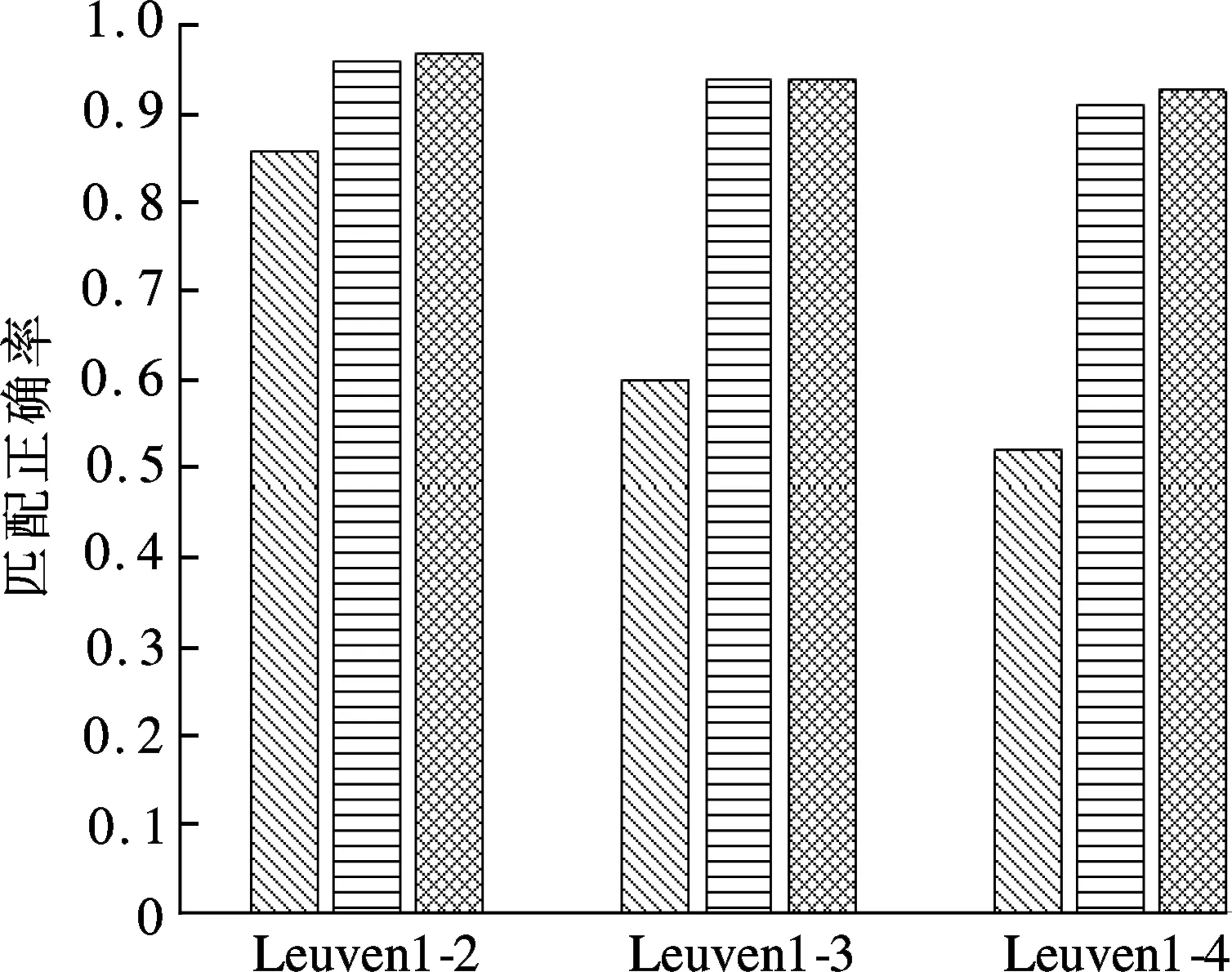
(b) Leuven组

(c) Btree组

(d) Compa组

通过仿射变换将参考图像标定在待配准图像上.图4是Graf组中的图像对1-3配准之后的效果,左边是参考图像,右边是视点变化之后的待配准图像,图中的小圆圈代表检测到的特征点,实线连接的是2幅图像中对应的特征点.最后在待配准图像中,用实线框将左边的参考图像标定出来.

图4 配准结果样例

4 结语

本文针对现有图像特征提取算法无法保持图像局部精度和边缘细节等缺点,基于A-KAZE算法提出一种基于改进LDB描述子的特征提取算法用于图像配准.以4种不同类型的同一场景的图像进行配准实验,构造非线性图像金字塔,采用FED方法求解特征点,使用ILDB描述子进行特征点的向量描述,最后进行图像配准.实验结果表明,相比于原始的A-KAZE算法,本文算法平均配准时间减少约300 ms,并且保持了图像的局部精度和边缘细节,配准精确度相比于传统的SURF算法也有很大提高.

References)

[1]Rohilla J, Bhatnagar M A. Image registration: A review[J].InternationalJournalforInnovativeResearchinScience&Technology, 2016,3(2):90-93.

[2]Nasrollahi K, Moeslund T B. Super-resolution: A comprehensive survey[J].MachineVisionandApplications, 2014, 25(6):1423-1468. DOI:10.1007/s00138-014-0623-4.

[3]Tian J, Ma K K. A survey on super-resolution imaging[J].Signal,ImageandVideoProcessing, 2011, 5(3):329-342. DOI:10.1007/s11760-010-0204-6.

[4]Li Y, Wang S, Tian Q, et al. A survey of recent advances in visual feature detection[J].Neurocomputing, 2015, 149:736-751. DOI:10.1016/j.neucom.2014.08.003.

[5]Sun Y B, Zhao L, Huang S D, et al. L2-SIFT: SIFT feature extraction and matching for large images in large-scale aerial photogrammetry[J].ISPRSJournalofPhotogrammetry&RemoteSensing, 2014, 91:1-16.

[6]Gui Y, Su A, Du J. Point-pattern matching method using SURF and shape context[J].Optik—InternationalJournalforLightandElectronOptics, 2013, 124(14): 1869-1873. DOI:10.1016/j.ijleo.2012.05.037.

[7]Alcantarilla P F, Bartoli A, Davison A J. KAZE features[C]//ComputerVision—ECCV2012. Berlin: Springer, 2012:214-227. DOI:10.1007/978-3-642-33783-3_16.

[8]Weickert J, Grewenig S, Schroers C, et al. Cyclic schemes for PDE-based image analysis[J].InternationalJournalofComputerVision, 2016, 118(3): 275-299.DOI:10.1007/s11263-015-0874-1.

[9]Alcantarilla P F, Jesú N, Bartoli A. Fast explicit diffusion for accelerated features in nonlinear scale spaces[C]//ElectronicProceedingsoftheBritishMachineVisionConference. Bristol, UK, 2013:1-11.

[10]Grewenig S, Weickert J, Bruhn A. From box filtering to fast explicit diffusion[J].LectureNotesinComputerScience, 2010, 6376: 533-542. DOI:10.1007/978-3-642-15986-2_54.

[11]Yang X, Cheng K T. LDB: An ultra-fast feature for scalable augmented reality on mobile devices[C]//IEEEInternationalSymposiumonMixedandAugmentedReality. Atlanta, USA, 2012:49-57.

[12]Tuytelaars T, Mikoljczyk K. Affine covariant features[EB/OL]. (2008) [2016-03-03]. http://www.robots.ox.ac.uk/～vgg/research/affine.

[13]Mikolajczyk K, Schmid C. A performance evaluation of local descriptors[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005, 27(10): 1615-1630. DOI:10.1109/TPAMI.2005.188.

Application of improved A-KAZE algorithm in image registration

Wu Hanqian1,2Li Chengchao1,2Xie Jue3

(1School of Computer Science and Engineering, Southeast University, Nanjing 210018, China) (2Key Laboratory of Computer Network and Information Integration of Ministry of Education, Southeast University, Nanjing 210018, China) (3Southeast University-Monash University Joint Graduate School, Suzhou 215123, China)

Aiming at the problem that local precision and edge details are difficult to preserve in the existing process of image registration, an improved image feature extraction algorithm AKAZE-ILDB(accelerated KAZE-improved local difference binary) is proposed based on the A-KAZE algorithm. First, this algorithm uses nonlinear diffusion filtering equation to construct the image pyramid. The numerical solution is obtained by the fast explicit diffusion(FED) method. The coordinates of the image feature points with subpixel precision are obtained. Then, the invariant image feature vectors are constructed by the improved LDB descriptor. The eigenvectors are matched by KNN(K-nearest neighbor) with Hamming distance. Finally, the spatial mapping parameter matrix is computed based on the affine transformation model to realize image registration. The experimental results show that in terms of registration efficiency, the AKAZE-ILDB algorithm reduces average registration time by 300 ms compared with the original A-KAZE algorithm in the condition of maintaining the same matching accuracy. Meanwhile, the matching accuracy of the same image feature is also improved by 3.7% higher than the A-KAZE algorithm and 29% higher than the traditional feature extraction algorithm SURF(speed up robust feature).

A-KAZE; nonlinear diffusion filter; fast explicit diffusion(FED); K-nearest neighbor matching; affine transformation

10.3969/j.issn.1001-0505.2017.04.007

2016-11-13. 作者简介: 吴含前(1972—)，男，博士，副教授， hanqian@seu.edu.cn.

国家高技术研究发展计划(863计划) 资助项目(2015AA015904).

吴含前,李程超,谢珏.一种改进的A-KAZE算法在图像配准中的应用[J].东南大学学报(自然科学版),2017,47(4):667-672.

10.3969/j.issn.1001-0505.2017.04.007.

TP315.69

A

1001-0505(2017)04-0667-06