基于狄杰斯特拉算法的蔬菜种植和配送最优化

姜思源，曹春玲，孟超，浦东，王凯琪

（吉林大学 数学学院，长春 130022）

基于狄杰斯特拉算法的蔬菜种植和配送最优化

姜思源，曹春玲，孟超，浦东，王凯琪

（吉林大学 数学学院，长春 130022）

采用狄杰斯特拉（Dijkstra）最优化理论，对城市周边的蔬菜种植和配送建立数学模型，在考虑增加蔬菜种植量同时各蔬菜销售点的短缺量一律不超过需求量的30%的情况下，实现了总短缺补偿和运费补贴最少。对“菜篮子工程”具有一定的指导意义和应用价值。

狄杰斯特拉算法；菜篮子工程；蔬菜配送方案

为缓解我国副食品供不应求的矛盾，农业部于1988年提出建设“菜篮子工程”，以保证居民一年四季都有新鲜的副食品供应。对于一些中小城市，蔬菜种植采取以郊区和农区种植为主，结合政府补贴的方式来保障城区蔬菜的供应。这样不仅提高了城区蔬菜供应的数量和质量，还带动了郊区和农区菜农种植蔬菜的积极性。但由于地区差异，蔬菜产区过于分散使其在种植区域和运输路径、配送成本上存在很多问题。因此采用最优算法对蔬菜配送路径进行优化就显得尤为重要。

最优路径算法是路径分析中最常用的算法之一。在很多领域都应用非常广泛，例如车载导航系统、智慧交通系统等都离不开最优路径算法的应用。本文在详细分析了某市蔬菜基地与销售点交通路线情况的基础上，应用最优算法中经典的狄杰斯特拉（Dijkstra）最短路径法分析得出从蔬菜基地到不同销售点的最佳运送路线，并从减少政府补贴的角度出发，建立目标函数和相应的约束条件，进行参数优化，得出不同要求下的最佳运送方案和补贴金额。从而为企业提供实时蔬菜配送最优路径和管理手段，提高企业和社会效益。

1 狄杰斯特拉最优化算法研究

狄杰斯特拉算法［1］（Dijkstra）是由荷兰计算机科学家狄杰斯特拉于1959年提出，应用贪心算法模式，是目前公认的最好的求解最短路径的方法。算法解决的是图中单个源点到其他顶点的最短路径问题，其主要特点是每次迭代时选择的下一个顶点是标记点之外距离源点最近的顶点。狄杰斯特拉算法属于图论中关于最优路径的算法。

表1 蔬菜运送距离

狄杰斯特拉算法的基本思想是按距离u0从近到远的顺序，以此求得u0到G的各项顶点的最短路径和距离，直到v0（或直到G的所有顶点），算法结束。为避免重复并保留每一步的计算信息，采用标号算法。算法实现如下

（1）令l(u0)=0，对v≠u0，令l(v)=∞ ，S0={u0}，i=0。

（3）若i=|v|-1，停止；若i＜|v|-1，用i+1替代i，转第2步。

算法结束时，从u0到各顶点v的距离由v的最后一次的标号l(v)给出。在v进入Si之前的标号l(v)叫T标号，v进入Si时的标号l(v)叫P标号。算法就是不断修改各顶点的T标号，直至获得P标号。若在算法运行过程中，将每一顶点获得P标号所由来的边在图上标明，则算法结束时，u0至各项点的最短路径即可在图上标示出来。

2 蔬菜最优化种植和配送

本文主要研究某市蔬菜种植和配送的最优方案，通过调研蔬菜基地、蔬菜销售点及相互位置关系和交通状况，得出某市蔬菜基地、路口和销售点三者之间的位置关系，如图1所示。结合图论相关理论，建立各个蔬菜基地、路口和销售点的邻接矩阵，应用狄杰斯特拉算法，利用Matlab软件实现算法，得出从蔬菜基地到各个销售点的最短运输路线，如表1所示。运输补贴正比于运输量和运输距离，因此每个种植基地运往每个销售点的蔬菜可以单独运输，所以选择两地之间最短路线运送蔬菜即可使总运费补贴最少。

本模型中假设运送蔬菜的汽车数量足够多，当选择最短的运送路线时可以使政府的运费补贴最少，从而使政府的补贴总额达到最低，因而在本模型中蔬菜运送路线选择表1所述的最短路线。

设i表示基地编号，j表示销售点编号，yij表示基地i对销售点j运送量；pj表示销售点的需求量，dij表示运送总路程，Mj表示短缺补偿；C表示政府的补贴总额，则补贴总额的目标函数如下：

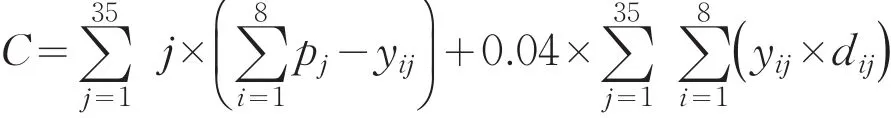
根据调研给出8个基地的产量和35个销售点的需求量见表2和表3，建立8个基地的产量、35个销售点的需求量与运送量约束关系，其中Gi表示基地产量。

表2 蔬菜种植基地日供应量（吨/天）

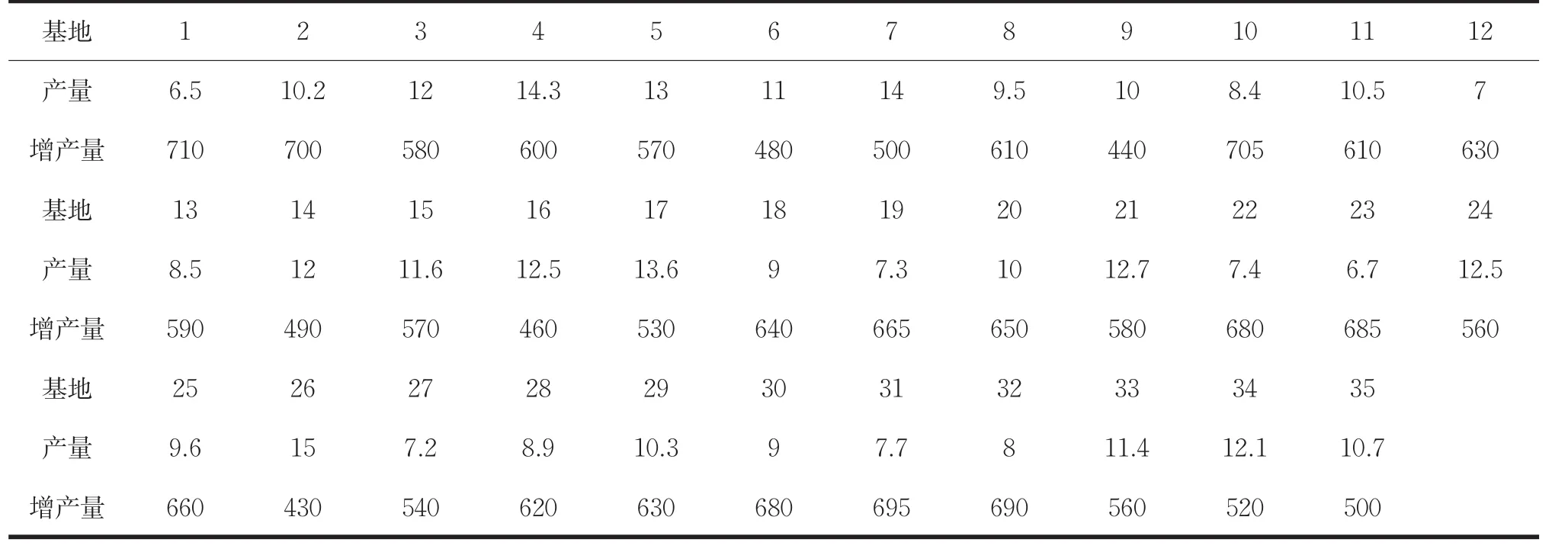
表3 蔬菜销售点日需求量（吨/天）及短缺补偿（元/吨.天）

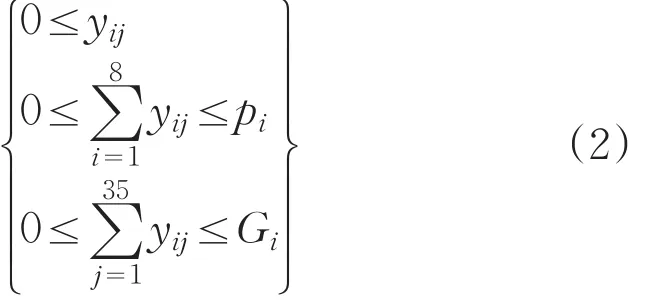
利用Lingo软件，编程可以得到最优条件下的蔬菜配送方案和配送量，利用公式1可以计算出最优配送方案下对应的补贴值C=42821.66元。当存在短缺量上线限制时，在原有约束条件中加入短缺上限条件，使短缺量上限小于需求量的30%。

利用Lingo软件，编程可以得到使短缺量上限小于需求量的30%时最优条件下的蔬菜配送方案和配送量，见表4。根据公式1得到存在短缺上限时的最优政府补贴总额C=50469.61元

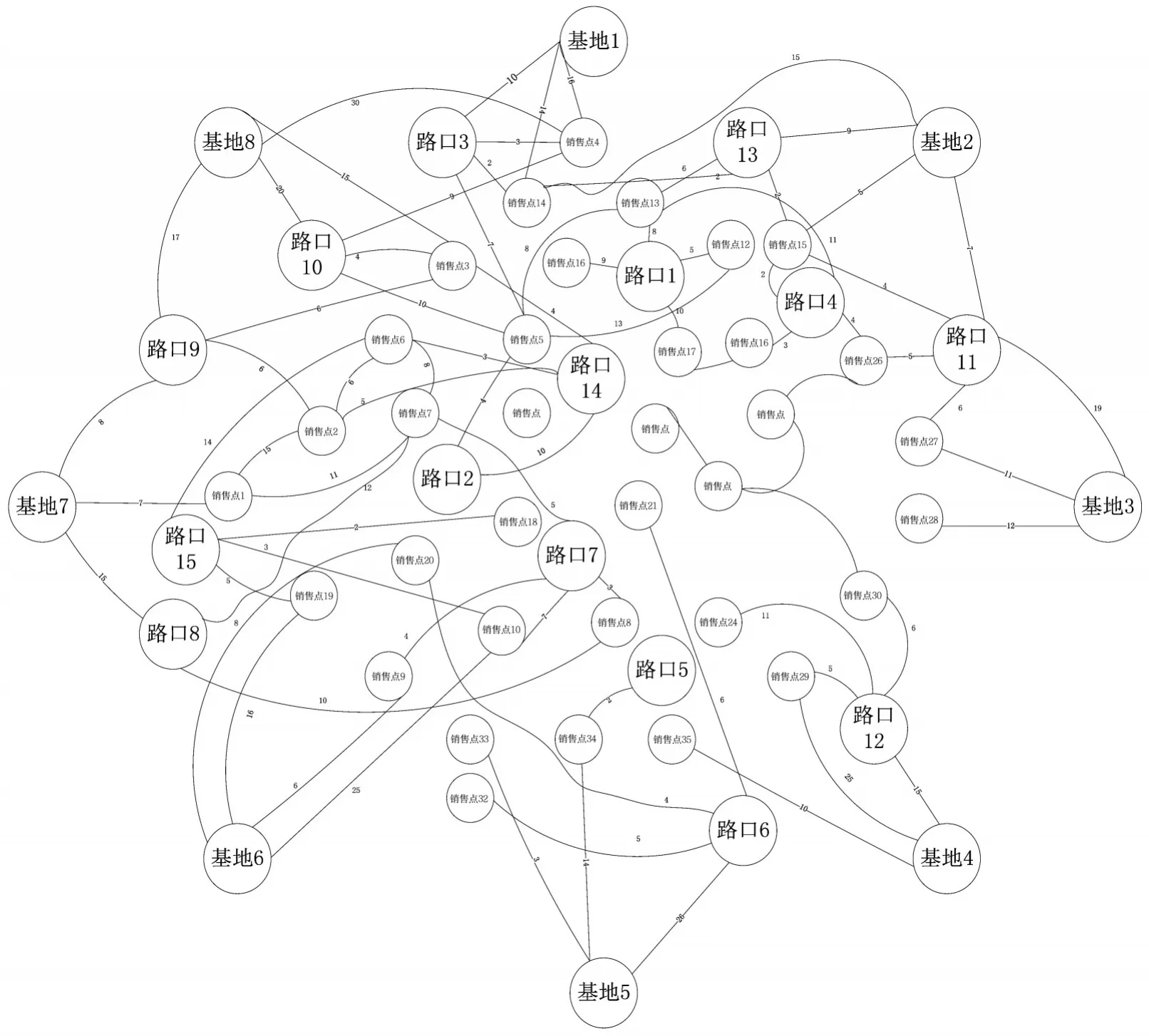
图1 蔬菜基地、路口和销售点的位置图

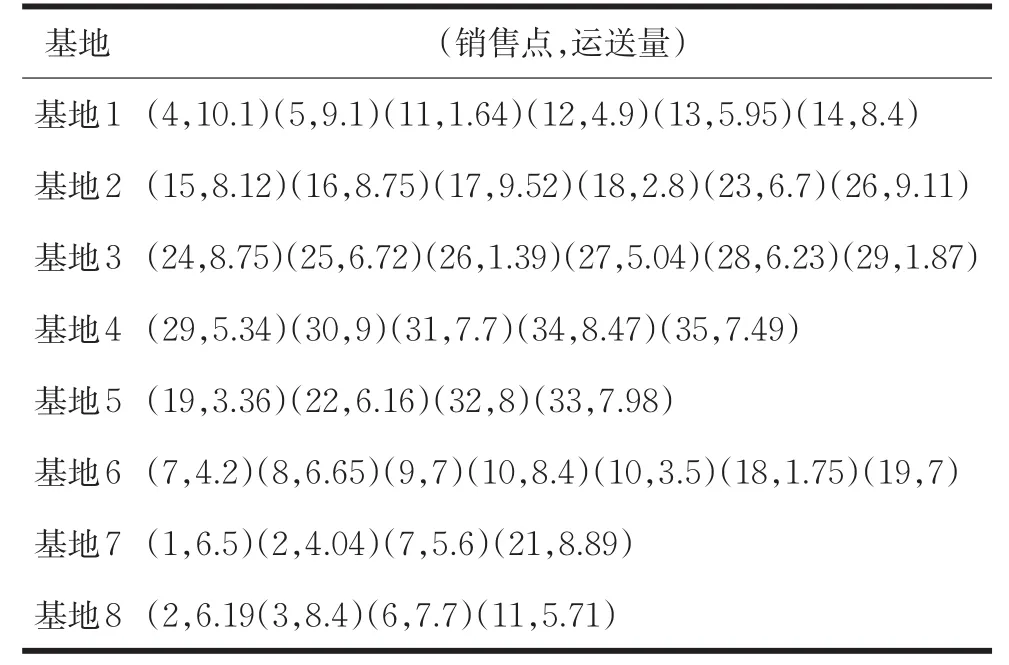
表4 短缺量上限小于需求量的30%条件下的最优蔬菜配送方案和配送量

根据前面最优化分析得到最优条件下的蔬菜配送方案和配送量。但在实际配送过程中，要考虑不同销售点的实际需求量。因此需在此基础上对模型进行调整，利用前面分析中得到的最佳运输路线。以满足各个销售点的需求量为原则，采用逆向分配的方法，由销售点向种植基地分配供应量。建立约束条件，结合目标函数，从而得出各个基地的增产和蔬菜运输方案，获得最佳的政府补贴方案。得出增产后的配送方案和补贴金额，由增产前后蔬菜基地的产量得到各个基地所需增加的种植量。在分析中对部分基地的蔬菜种植面积进行扩大。通过分析发现相对于短缺补贴，运费补贴对政府总补贴额度的影响相对较小，因而在尽可能满足供应的条件下建立约束条件，在部分基地无产量上限的约束下使运费达到最少。目标函数和约束条件如下：

利用Lingo软件计算，可以得到最低补贴的运送方案，根据目标函数，得到最优政府补贴总额为C=182.204元，补贴数额极小，实现了最优化结果。

根据Lingo的运算结果，可以得到增产状态下各基地的种植数量，通过与表2中给出的每个基地的产量进行对比，得出增产方案，如表5所示。

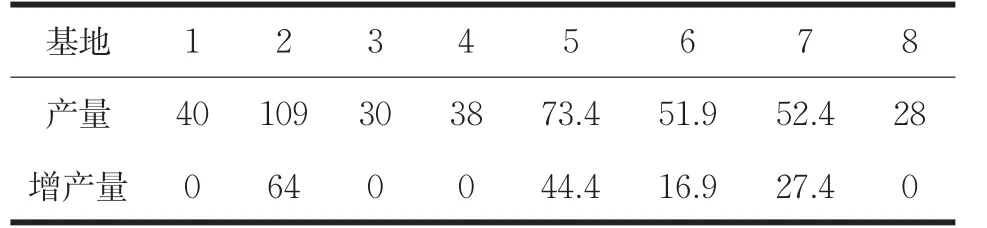
表5 基地产量与增产量

3 结论

本文研究了某市蔬菜生产基地与各个路口和蔬菜销售基地的位置关系和交通状况，应用狄杰斯特拉算法，得出从蔬菜基地到各个销售点的最短运输路线，即总运费补贴最少。考虑供应量和需求量，以满足各个销售点的需求量为原则，采用逆向分配的方法，由销售点向种植基地分配供应量。建立约束条件，结合目标函数，从而得出各个基地的增产和蔬菜运输方案，获得最佳的政府补贴方案。模型的复杂性和运算量低，实用性好，具有很强的现实应用指导意义。

［1］ 樊月珍，江发潮，毛恩荣.车辆行驶最优路径优化算法设计［J］.计算机工程与设计，2007，28（23）：5758-5761.

［2］ 王树西，李安渝.Dijkstra算法中的多邻接点与多条最短路径问题［J］.计算机科学，2014，41（6）：217-224.

［3］ 张锦明，洪刚，文锐，等.Dijkstra最短路径算法优化策略［J］.测绘科学，2009，34（5）：105-106.

［4］ 周毕文，黄洁萍，李春华.线性规划最优解的探讨及在生产与运作管理中的应用［J］.北京理工大学学报，2001，3（4）：47-49.

［5］ 陈华友，周礼刚，刘金培.数学模型与数学建模［M］.北京：科学出版社，2014：116-118.

Vegetables Planting and Distribution Optimization Based on the Dijkstra Optimization Algorithm

JIANG Siyuan，CAO Chunling，MENG Chao，PU Dong WANG Kaiqi
（Institute of Mathematics，Jilin University，Changchun 130022）

The paper establish a mathematical model to the peri-urban vegetables planting and distribution base on the DiJie Stel⁃la（Dijkstra）optimization theory，considering the increase in the vegetables planting and all the shortage of vegetables point-ofsale amount shall not exceed 30%of the demand，realize the shortage of total compensation and minimumfreightsubsidies.thepaper hasacertainguidingsignificanceandapplicationvaluetothe“vegetablebasketproject”.

DiJie stella（Dijkstra）optimization theory；vegetable basket project；vegetable distribution scheme

TP301.6 1

A

1672-9870（2017）03-0130-04

2017-03-05

自然科学基金资助（J1310022）

姜思源（1996-），男，本科，E-mail：873879194@qq.com

曹春玲（1971-），女，副教授，E-mail：caocl@jlu.edu.cn