基于毕业要求达成度的薄弱课程诊断方法*
郭斯羽,温 和,汪 沨,孟志强,曹琳琳
(湖南大学 电气与信息工程学院,湖南 长沙410082)
基于毕业要求达成度的薄弱课程诊断方法*
郭斯羽,温 和,汪 沨,孟志强,曹琳琳
(湖南大学 电气与信息工程学院,湖南 长沙410082)
毕业要求达成度评价是工程教育认证中的重要工作。为了将毕业要求达成度评价的结果用于专业的持续改进,本文提出了一种达成度量化分析的方法。本方法利用修课学生在课程相关毕业要求指标点上的平均达成度来衡量学生总体的达成情况,在设置和分配毕业要求目标达成度后,将学生在课程中获得的指标点平均达成度与目标值相比对,并经课程权重加权得到量化的课程对毕业要求达成的贡献值。通过该量化的贡献值,可以诊断出对达成度目标的实现贡献不足的课程,从而为有针对性的课程改进提供指向。
工程教育认证;毕业要求;持续改进
一、引言
毕业要求达成度评价是工程教育认证工作中一项极为重要的内容。根据学校和专业定位以及社会需求设置了专业培养目标、根据专业培养目标设置了毕业生能力目标即专业毕业要求后,需要通过毕业要求达成度评价来证明毕业生能力的达成。进行毕业要求达成度评价至少包括以下两个作用:通过毕业要求达成度评价来证明本专业毕业生在所需的能力上“合格”了;(2)通过毕业要求达成度评价和分析来诊断和发现培养过程中的薄弱环节,并据此开展持续改进。
随着近年来工程教育认证工作的持续开展,关于专业毕业要求的设置与评价,已经有若干研究者提出了有益的看法与见解[1-5]。不过这些文献主要关注于本专业的毕业要求设置与指标点分解的思路,以及从考察毕业生是否合格的目的出发,如何开展和应用毕业要求达成度评价。在持续改进方面,已有的文献多注重于通过毕业生以及用人单位的反馈来衡量专业的培养质量[6,7],但是在校内充分利用毕业要求达成度评价的结果来诊断特别是定量诊断整个教学过程的薄弱环节,并据此进行有针对性的改进,这一方面的工作目前还较少见诸文献之中。
本文给出了一种方法,用于量化地分析和衡量各门课程对于毕业要求达成度的贡献,并据此发现其中对毕业要求达成影响最大、最亟待改进的课程,以便采取有针对性的措施来提高教学质量。
二、学生个人的毕业要求达成度评价
进行毕业要求达成度评价的常见的做法如下:
令R表示专业所有毕业要求的集合。
(1)将专业的每项毕业要求r∈R细分为若干更具有可操作性的“指标点”或“能力要素”。记毕业要求r的指标点集合为A(r),而所有指标点的集合为A,则这一指标点划分显然应满足
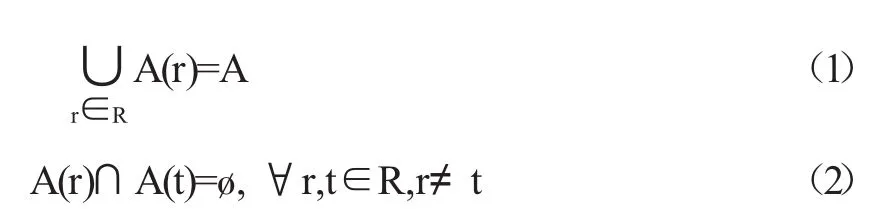
(2)每个指标点a∈A的达成需要通过若干门课程来实现,即在课程中对相关能力要素进行培养,并对能力达成的情况进行考核。称这些课程“支撑”了该指标点。令C为所有课程的集合,对于指标点a,给每门课程c∈C赋予一个非负的支撑权重w(a,c),且所有课程对指标点a的支撑权重之和为1,即

显然,若课程c不支撑指标点a,则有w(a,c)=0;但另一方面,在进行毕业要求达成度评价时,推荐对每个指标点a,仅使用少数几门(通常是2到3门)支撑作用最为明显的课程来进行评价,因此对于其余的弱支撑课程,仍然将其权重w(a,c)设置为0;
(3)每门课程c应通过有效手段(如书面考试、作业、报告、实验等方式)来对学生在该课程所支撑的指标点上的达成情况进行量化的考核或评估。记学生s在课程c中,在指标点a上的达成度评估值为pC(s,a,c)。pC(s,a,c)在归一化的[0,1]区间上取值,专业可根据合理的规则将百分制、等级制等其他形式的评估结果转化为归一化的达成度评价值。为了表述方便,如果c并非a的支撑课程,则令pC(s,a,c)=0;
(4)某名学生s在指标点a上的达成度pA(s,a),等于该生在a的各门课程c中获得的该指标点达成度pC(s,a,c),经课程权重w(a,c)加权后求和而得,即
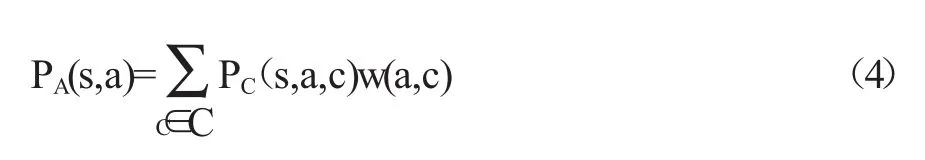
显然,pA(s,a)的取值范围也是[0,1]区间。
三、学生整体的毕业要求达成度评价
如果希望通过毕业要求达成度评价来考核某届毕业生是否均为“合格”,则此时毕业生能力的达成情况由“最短的一块板”所决定,即全体学生的毕业要求达成度由达成度最低的那名学生所确定,每名学生的毕业要求达成度由达成度最低的那项毕业要求所决定,而每名学生在某项毕业要求上的达成度又由其下各指标点的最低达成度所决定。以公式表示便是

式中,S表示全体被评价学生的集合,pG(S)表示学生集合S的总的毕业要求达成度。如果pG(S)达到某个专业设定的阈值,则认为被评价学生总体达成了毕业要求。
但是,如果希望通过毕业要求达成度评价来考察某届毕业生的“整体达成情况”,以此衡量教学过程的“整体培养质量”并据此进行教学过程的持续改进,那么使用上述最短板的方式显然有失偏颇,而更合理的做法是使用某种“平均达成度”来衡量整体的达成情况。由于我们希望通过达成度评价来对课程的教学质量进行诊断,而课程的主要任务是针对指标点所体现的能力要素进行培养与考核,因此我们考察指标点的“平均达成度”。
记全体被评价学生S在课程c中、在指标点a上取得的平均达成度为qC(S,a,c)。一般S取为在课程c的一次授课中修读该课程的全体学生。常用的平均达成度可以取算术平均值,即

式中,||S||表示被评价学生的人数;平均达成度也可以取中值,即
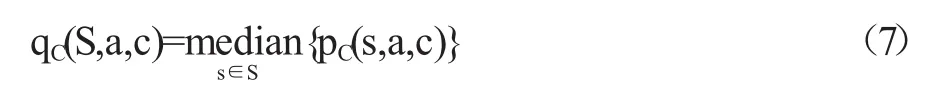
类似地,记S在指标点a上的平均达成度为qA(S,a)。qA(S,a)同样可以取算术平均值

或中值

S在每项毕业要求r上的达成度qR(S,r)以及总的毕业要求达成度qG(S)仍然按最小值求取,即

四、课程对毕业要求达成度的贡献
为了分析课程对于毕业要求达成度的贡献,并发现相对薄弱的课程,我们首先设置一个总的毕业要求达成度的目标值gG,这一目标值体现了我们所认为的、符合现阶段专业实际的一个良好的达成度。如果被评价对象的总的毕业要求达成度qG(S)不小于gG,则认为毕业要求达成情况是令人满意的,否则即认为存在明显需要改进的课程。
然后,将gG分配到每个毕业要求r上。由于总的毕业要求达成度由各个毕业要求的达成度的最小值所决定,因此一般可以自然地要求每个毕业要求r的毕业要求达成度目标值gR(r)=gG。当然,如果认为对不同的毕业要求应设置不同的目标值,也同样是可行的,只要满足gR(r)莛gG即可。
类似地,我们可以将gR(r)进一步分配给每项指标点a∈A(r),从而得到每项指标点的达成度目标值gA(a)。同样地,只要设置的目标值满足 gA(a)莛gR(r),a∈A(r),就都是合理的。不过一般为简便计,可以取gA(a)=gG。
再进一步,我们可以将gA(a)分配给a的各个支撑课程c,获得课程c中对指标点a的达成度目标值gC(a,c)。由于指标点a的达成度是根据式(4)按加权和的方式由各个支撑课程中a的达成度求得,因此自然地想法是根据不同支撑课程对于指标点a所体现能力要素的要求高低,对各门支撑课程c分别赋予不同的gC(a,c),只要它们满足
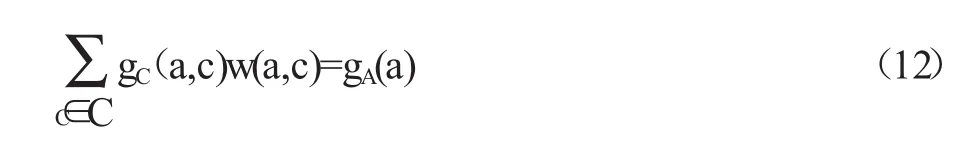
作为一个简化但合理的特殊情形,我们可以对所有支撑课程c均设置gC(a,c)=gA(a)=gG。
在此需要注意,如果使用算术平均值来计算平均达成度qC(S,a,c)和qA(S,a),由于算术平均和加权和式(4)均为线性操作,因此两者次序可以调换,即
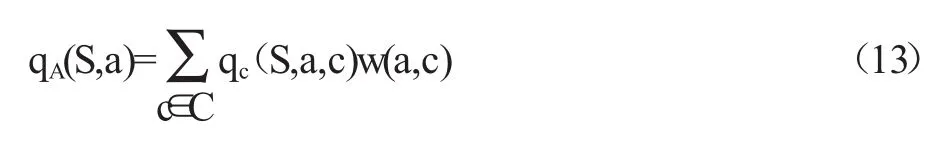
如果gC(a,c)满足式(12),那么当各门支撑课程的qC(S,a,c)达到了本课程中a的目标达成度时,自然可以保证qA(S,a)也就达到了指标点a的总的目标达成度。但是如果使用中值计算平均达成度,则这一点无法从理论上得到保证,只是在比较正常的情况下,当课程中指标点达成度中值较明显地低于或高于目标达成度时,指标点总的达成度的中值通常也不会给出质变的结果。由于中值对于学生的达成度中的极端值更不敏感,一般较算术平均值更能体现总体的实际达成情况,因此我们在使用中值计算平均达成度时,也仍然按式(12)的方式来设置课程中指标点的目标达成度。
将式(12)和(13)相减可得
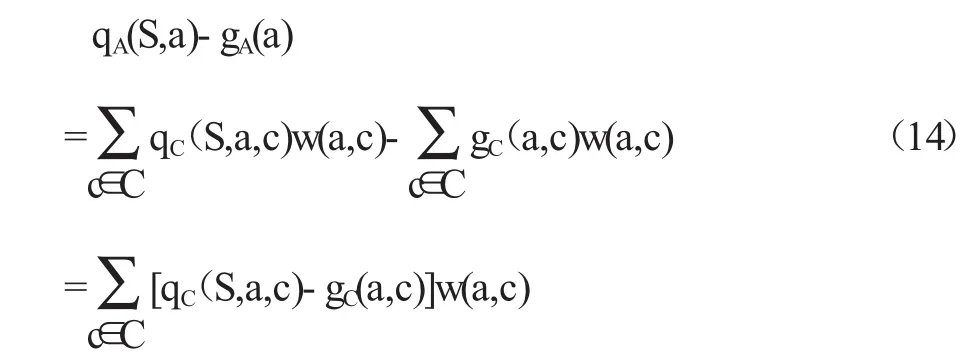
式(14)的第一个等号左侧项的含义是被评价对象S在指标点a上的平均达成度与指标点a的目标达成度之间的差值,而第二个等号右侧项中的qC(S,a,c)-gC(a,c)的含义则是被评价对象S在课程c中获得的指标点a的平均达成度与c中a的目标达成度的差值。可见指标点a的总达成度与目标达成度之间的偏离,是由各支撑课程中a的达成度与目标达成度之间的偏离经w(a,c)加权后求和而得。由式(14)可以清楚看出,一门课程c对于指标点a的达成情况的“贡献值”可以合理地用b(S,a,c)=[qC(S,a,c)-gC(a,c)]w(a,c)加以定量描述:b(S,a,c)>0表明课程c对于a的达成起到了正面作用,而b(S,a,c)<0则表明课程c需要改进,以使学生在课程中掌握的能力要素a能够满足期望的要求。
同样,式(14)对于使用算术平均的平均达成度是成立的,而对于中值不保证成立,不过此时我们仍然可以采用相同的方式来估计各门课程的贡献。
最后,我们可以将每门课程的“最大正贡献值”和“最小负贡献值”以条状图的形式进行显示,以便直观地看出各门课程以及不同类型的课程组对于毕业要求的影响大小,并采取针对性的措施进行改进。
五、示例
现以某校某专业为例,说明上述分析方法的应用。该专业培养方案中共包括68门课程(必修、专业选修、实践环节等),专业制订了12项毕业要求,共分为41个指标点。下面以“电路”课程来说明课程对毕业要求达成度贡献值的计算。“电路”课程共支撑了2个毕业要求的5个指标点,这5个指标点各自的支撑权重见表1。

表1 “电路”课程支撑的指标点及权重
在一次授课中,修读“电路”课程的学生人数共51人。课程通过平时作业、期中测验、期末考试、小班讨论等方式,就各个指标点对学生进行了考核,考核结果如表2所示,其中我们采用中值作为平均达成度的指标。
专业设置了毕业要求的目标达成度gG=0.8,并等值分配到了各门课程的各个指标点上,即对所有指标点a和所有课程c,取gC(a,c)=0.8。于是指标点1.2的达成度为0.758<0.8,表明“电路”课程对于毕业要求的达成的贡献偏负面,未能达到专业期望的目标。这一贡献值可量化地计算为(0.758-0.8)×0.3=-0.0126。类似可计算得到“电路”课程在指标点3.1、3.2、3.3和3.4上的达成度贡献值分别为-0.0142、0.0060、-0.0050和-0.0180。可见,“电路”课程对于毕业要求达成度的最大正面贡献值为0.0060(指标点3.2),而最小的负面贡献值为-0.0180(指标点3.4)。这一量化结果表明“电路”课程可总结在培养指标点3.2方面的有益经验,而需要其他指标点的教学过程加以审视和改进,其中最为迫切的就是指标点3.4的教学过程。类似可以计算出各门课程对毕业要求达成度目标的贡献值,并绘制成如图1所示的条状图。
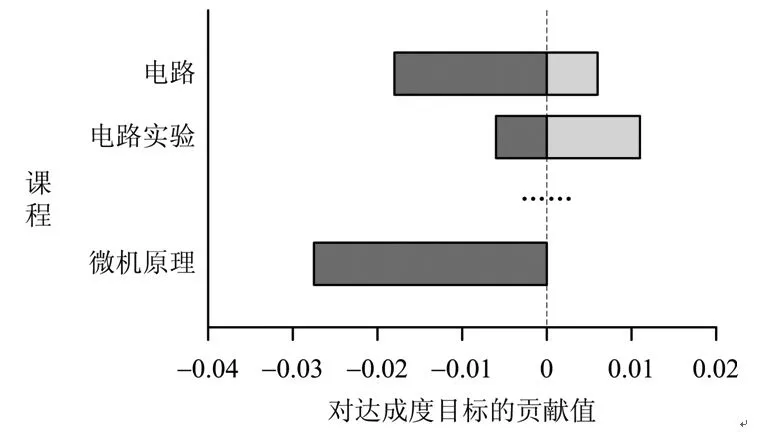
图1 各课程对达成度目标贡献的条状图
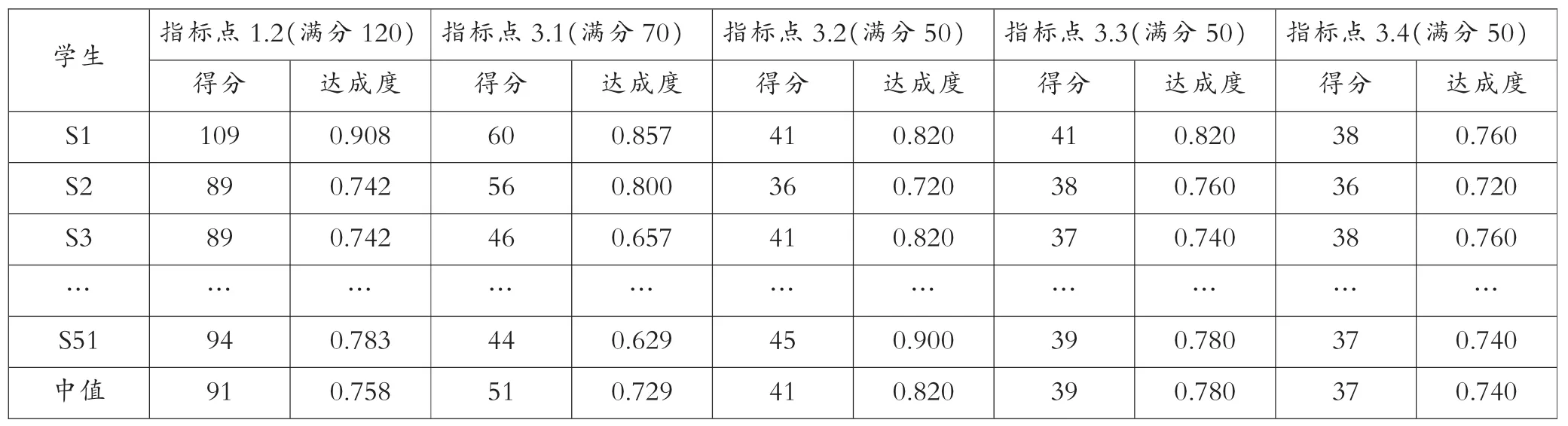
表2 被评价学生在“电路”课程所支撑的各指标点上的考核得分与达成度
[1]顾晓薇,王青,邱景平,胥孝川,张春明.工程教育认证“毕业要求”达成度的认识与思考[J].教育教学论坛,2016,(14):24-26.
[2]李青竹,肖睿洋,闵小波.对工程教育专业认证中“毕业要求”的理解——以中南大学环境工程专业为例[J].学园,2015,(24):21-22.
[3]欧红香,葛秀坤,邢志祥.毕业要求达成度评价体系探究——以安全工程专业认证为例[J].黑龙江教育(高教研究与评估),2015,(10):4-5.
[4]王世勇,董玮,郑俊生,刘龙.基于工程教育专业认证标准的毕业生毕业要求达成度评估方法研究与实践[J].工业和信息化教育,2016,(3):15-22.
[5]邵辉,陈群,徐守坤,陈海群,张凤娥,单雪影.安全工程专业毕业要求达成度定量评估——基于跟进式教育理念的视角 [J].常州大学学报 (社会科学版),2015,16(3):114-117.
[6]余天佐,蒋建伟,任锐,刘少雪,庄颖.基于工程教育认证标准的持续质量改进——以Z大学全国示范性软件工程专业为例 [J].清华大学教育研究,2015,36(6):104-111.
[7]柳勤,唐水源,冯慧华,刘志兵,郝浩倩.工程教育认证中专业建设持续改进的毕业生跟踪反馈机制构建初探——以北京理工大学机械工程专业为例[J].工业和信息化教育,2016,(3):1-4.
(编辑:郭桂真)
G642
A
1673-8454(2017)14-0013-04
湖南省普通高等学校教学改革研究项目 “面向MOOC的 《数字图像处理》可视化编程远程实验系统研究”(521293198);湖南大学教学改革研究项目“面向MOOC的《科学与工程计算方法及应用》远程实验系统研究”(521202085);教育部卓越工程师计划项目:湖南大学测控技术与仪器(教高〔2011〕1号);全国专业改革综合试点项目:湖南大学测控技术与仪器专业综合改革(教高司函[2011]226号)。

