无形资产评估中灰色关联分析法研究
谢如松 李晓伟 谢肖琳
(1.江苏中天资产评估事务所有限公司;2.安徽省林业调查规划院)
无形资产评估中灰色关联分析法研究
谢如松1李晓伟2谢肖琳1
(1.江苏中天资产评估事务所有限公司;2.安徽省林业调查规划院)
为了得出合理、真实的待评估无形资产价值,本文阐述了无形资产评估中收益法的原理及具体应用过程中采用灰色关联分析法确定各可比上市公司关联度大小和所占权重的问题,进而选择与待评企业关联度大的可比上市公司并用加权平均法计算折现率,以期评价结果更具合理性。
权重 折现率 灰色关联分析
一、引言
随着我国市场经济的愈发繁荣和国家对无形资产保护程度的加大,特别是互联网的高速发展以及“互联网+”的提出,无形资产在经济领域的地位及价值评估的市场需求越来越大。基于此,中国资产评估协会近期制定了相应的知识产权及文化企业无形资产评估指南并开展了排污权及“互联网+”等与无形资产评估相关的课题,这对于我国无形资产评估来说是一个极大的进歩。通过对这些工作的开展,无形资产评估受社会的承认和重视程度将显著提高。
无形资产评估方法分为市场法、成本法和收益法。在采用收益法评估无形资产时,根据待评无形资产的自身特点及收集到的资料等具体情况,其测算方法可分为成本利润法、约当投资法、边际分析法、和技术贡献率等,其中,技术贡献率运用最为广泛。但是,这些方法在具体评估参数选取上还存在许多不足,比如在运用技术贡献率时,需找到拥有类似无形资产的可比上市公司,通过对可比上市公司的分析得出一系列评价因子,计算出可比上市公司与待评企业的关联度以及无形资产的折现率,从而计算无形资产的价值。在实际工作当中,通过主观价值的判断寻找到的上市公司实例,因为个人局限性的问题会对结果产生影响,从而导致无形资产的准确性大打折扣。而灰色关联度分析方法的引入却可以很好地解决可比上市选择不准确的问题,该方法的关联度分析,剔除了主观对结果的影响,可以使各上市公司与评估对象之间的相似程度更精准,根据关联分析的结果,将几个上市公司关联度最大的作为选取的对象,再根据关联分析法得出各上市公司的权重,并利用加权平均方法确定折现率,从而使评估结果更加精确、科学。
二、无形资产评估收益法
(一)合理选择可比上市公司应用收益法评估时,折现率的取得主要取决于所收集的可比上市公司数据,因此,选择合适的可比上市公司是计算折现率的关键所在。本文利用灰色关联法从上市公司的主营业务、盈利能力、资产质量、债务风险及经营增长等方面对上市公司与待评企业的关联度进行分析,以期得到与待评估企业最具相关性并能最大限度反映待评企业真实状况的上市公司。
(二)正确地确定折现率在运用收益法评估无形资产时,如何较为科学、合理且客观的确定无形资产评估折现率,始终是业内难题。选择运用简单平均值还是加权平均值会对折现率产生影响,而折现率的微小偏差往往会导致评估结果出现很大偏差,最终必然影响投资决策的科学性。笔者认为利用加权平均法计算折现率更具科学性和合理性,计算公式如下:

其中,n为可比上市公司的个数,Wi为第i个可比上市公司所占权重,Pi为第i个可比上市公司无形资产折现率。
三、灰色关联分析方法
(一)灰色关联原理内部特性已知的信息系统,称为白色系统;把未知的或非确知的信息系统,称为黑色系统;把既含有已知的又含有未知的或非确知的信息系统,称为灰色系统。灰色系统理论主要是透过一定的方法去寻求系统中各因素之间的数值关系。因此,灰色关联度分析对于一个系统发展变化态势提供了量化的度量,非常适合动态历程分析。
(二)方法步骤
(1)确定反映系统行为特征的参考数列和影响系统行为的比较数列。比较数列即为一种影响系统行为的因素组成的数据序列,参考数列即为一种反映系统行为特征的数据序列。
(2)对参考数列和比较数列进行无量纲化处理。数据的量纲不一定相同,因为系统中各因素的物理意义并不相同,所以它们之间比较起来比较困难,或在比较时难以得到正确且满意的结论。因此在进行灰色关联度分析时,一般都要进行无量纲化的数据处理。
(3)求参考数列与比较数列的灰色关联系数ε1(k)。曲线间几何形状的差别程度叫做关联度,因此关联程度的衡量尺度可以用曲线间差值大小来表示。对于一个参考数列X0有若干个比较数列X1,X2,...,Xn,各比较数列与参考数列在各个时刻(即曲线中的各点)的关联系数ε1(k)可由下列公式:

(4)求关联度ri。因为关联系数是比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数值不止一个,而信息过于分散不便于进行整体性比较。因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,即求其平均值,作为比较数列与参考数列间关联程度的数量表示,关联度ri公式如下:

四、应用实例
假设本次评估专利权的价值,由于待评企业为非上市公司,其市场价值未知,无法测算其资产结构比率,但其资本结构与同行业的上市公司应有相同或相似的地方。为此,此次运用灰色关联度选取了目前在国内上市的与待评公司关联度最高的六家公司作为对比公司,并假设以所选取的对比上市公司作为未来委估技术受让方的可能蓝本或可比对象来分析委估专利权可能为其带来的收益。
(一)评价因子的选取企业绩效评价中的财务指标分析分为盈利能力状况、资产质量状况、债务风险状况、经营增长状况。本次研究根据企业实际情况选取的评价因子为净资产收益率、总资产报酬率、总资产周转率、应收账款周转率、资产负债率、速动比率、销售增长率和资本保值增长率。
(二)关联度及权重的计算
(1)确定反映企业整体状况的参考数列和影响企业整体价值的比较数列,其中各数列数据,如表1。
(2)求出参考数列与比较数列的灰色关联系数ε1(k)和关联度,如表2。
(3)选择关联度排名前六的上市公司作为待评资产的可比上市公司,依据测算出的关联度,求出各案例所占权重W,如表3。
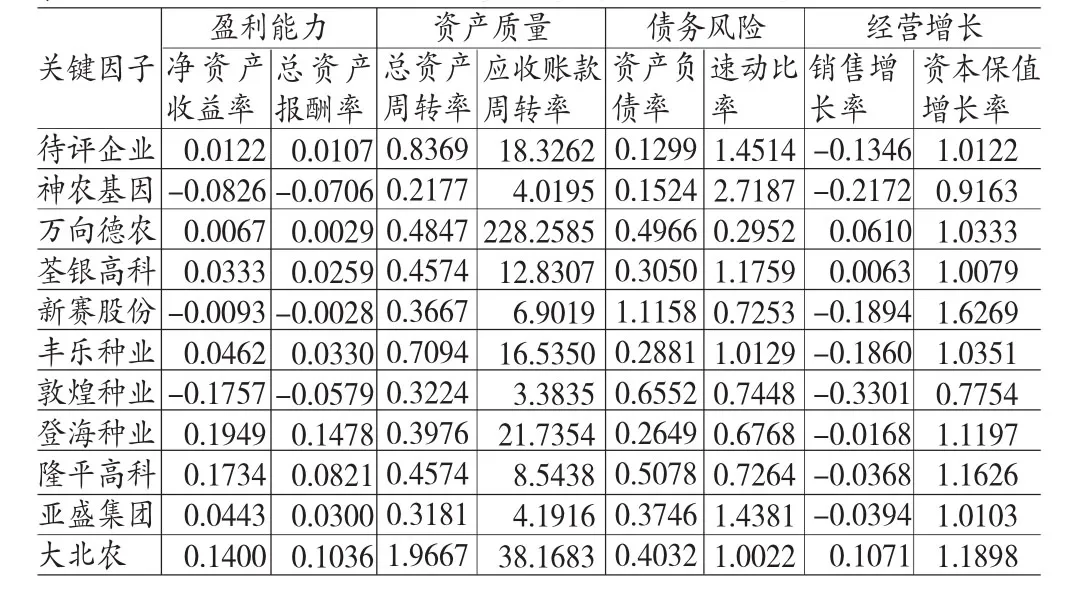
表1 评估案例和参照案例评价因子集合
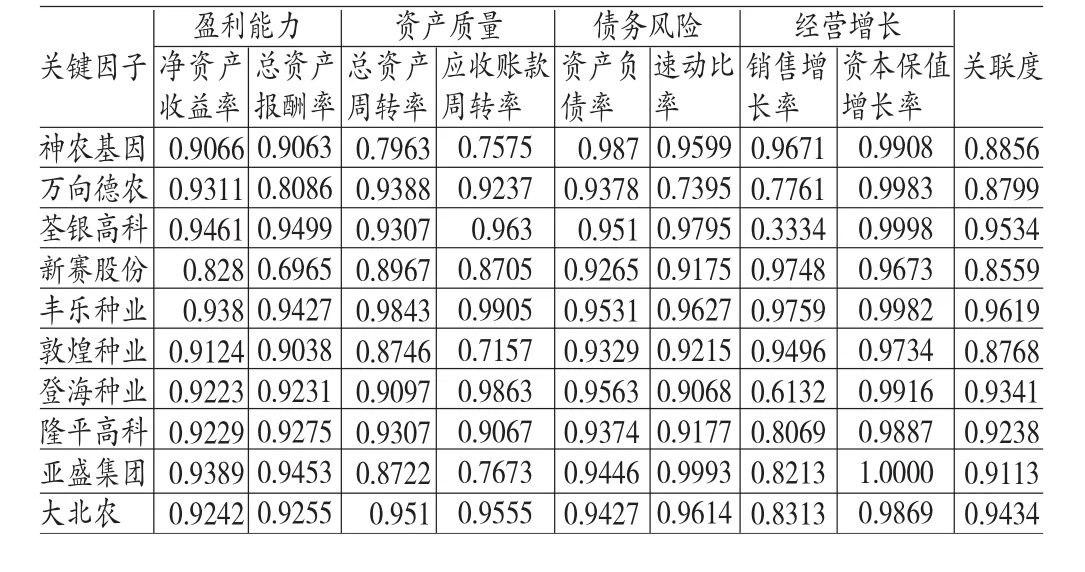
表2 关键因子间的关联系数、关联度

表3 参照案例的权重
(三)折现率的确定通过折现率的计算方法得出无形资产折现率计算表,如表4:
从表4可以看出,利用灰色关联求出关联度大的可比上市公司再应用简单平均法求得的无形资产折现率为:
利用灰色关联法选取关联度大的可比上市公司且求得权重,最后用加权平均法求出的无形资产折现率为:

未使用灰色关联法删选可比上市公司,而是随机选取六家可比上市公司且直接应用简单平均法得出的无形资产折现率,如表5:

表5 随机选择可比上市公司计算无形资产折现率
从参考案例权重求算的合理性角度出发,通过灰色关联度得到的无形资产回报率具有更高的可靠性。相比于简单平均法,基于灰色关联度的折现率充分考虑了参考案例的关键因素并做出合理的评判,所得到的案例权重值也体现了各案例的重要性,比简单平均法的均等权重更加科学。通过灰色关联度计算得出的折现率与随机组合计算的折现率的对比图,如图1:
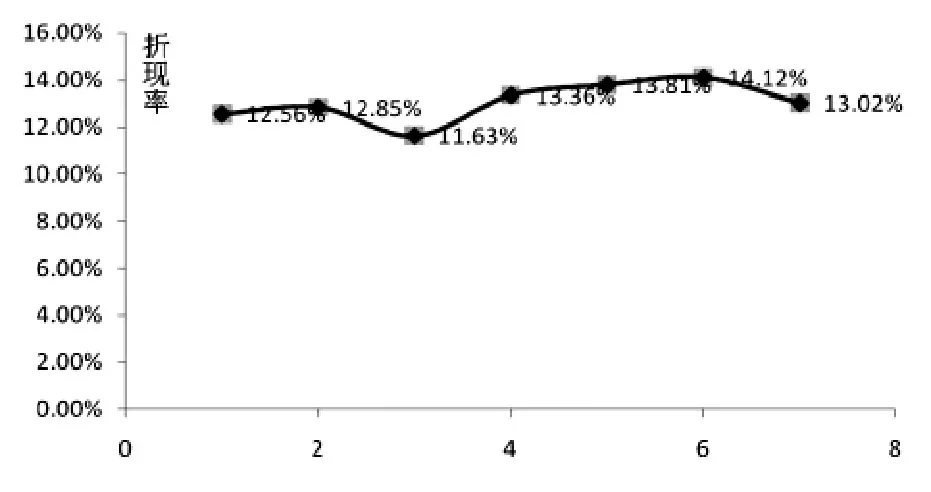
图1 灰色关联度计算的折现率与随机组合计算的折现率对比图
(四)评估值的确定
(1)利用灰色关联法选取可比上市公司并利用加权平均法计算得到无形资产折现率,再通过预测收入等,得到待评专利权评估结果,如表6:
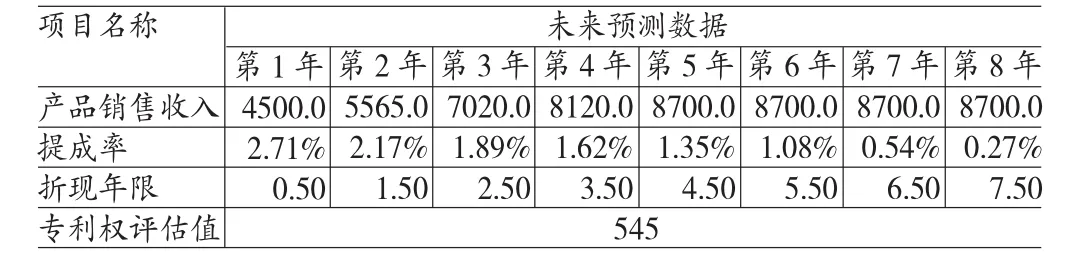
表6 专利权评估值(单位:万元)
(2)假设未利用灰色关联法计算折现率,而是随机选取可比上市公司进而使用简单平均法计算折现率,技术贡献率和收入等其它条件不变,得出专利权评估值,如表7:

表7 随机组合折现率下的专利权评估值(单位:万元)
(3)通过灰色关联法计算得出的折现率与随机组合计算的折现率的情况下得到的专利权评估值对比,如图2:

图2 灰色关联法计算的折现率与随机组合计算的折现率评估值对比图
通过对比分析可知,采用灰色关联分析法确定各可比上市公司关联度大小和所占权重,进而选择与待评企业关联度大的可比上市公司并用加权平均法计算的折现率得出的专利权评估值与随机选取可比上市公司并用简单平均法计算的折现率得出的评估值有所不同,最大差异为27万,差异率约为4.8%。因此,通过灰色关联分析能够准确的得到各可比上市公司与评估对象的相似程度,对选取可比上市公司进而用加权平均法求无形资产折现率有重要意义,并能使评估结果更加合理。
五、结论
灰色关联分析使各可比上市公司与评估对象的相似程度表现得更准确,因此可以通过关联度的计算得到与待评估企业最具相关性并能最大限度反映待评企业真实状况的上市公司。本文利用灰色关联法选取上市公司的盈利能力、资产质量、债务风险及经营增长等方面的基本指标作为评价因子,经计算,可比上市公司与待评企业关联度大小依次为:丰乐种业>荃银高科>大北农>登海种业>隆平高科>亚盛集团>神农基因>万向德农>敦煌种业>新赛股份。本次选择关联度排名前六的上市公司作为待评资产的可比上市公司,从而使选择的上市公司最具代表性。
通过数据的模拟和大量的应用,灰色关联分析对于优化决策中不确定性的定性量处理具有方法简单、应用效果良好,适用于方案优化选择等诸多优点。在应用收益法对无形资产评估的过程中,利用灰色关联法分析数据间的关联程度,对相关因子进行调整,并得出各可比上市公司所占权重,从而利用加权平均法测算出无形资产折现率,该结果将不同上市公司之间的差异和同一上市公司各关键因子的优劣都至直观的呈现出来,评价结果较为清晰,也比简单平均法更加合理。因此,使用这种分析方法计算无形资产折现率具有重要的现实意义。
[1]蒋勇、吴建刚:《灰色理论在收益现值法中的应用研究》,《中国资产评估》2000年第2期。
[2]胡晓晖:《谈无形资产评估中收益现值法应用的改进》,《当代财经》1999年第9期。
[3]Ackoff,R.L.Science in the Systems Age,Beyond IE. OR.and MS[J].Operations Research,1973,21(3):661-667.
[4]Bertranffy,L.V.GeneralSystemsTheory:Foundation Development,Applications[M].New York:George Braziller,1968.16-24.
[5]Chen Yaokai and Tan Xuerui.Grey Relational Analysis on Serum Markers of Liver Fibrosis[J].The Journal of Grey System,1995,7(1):60-68.
[6]Churchman,G.W.TheSystemsApprochandIts Enemies[M].New York,Basic Books,1979.50-52.
[7]Robert,A.D.and Kenneth,D.R.Management Science[M].New York,Macmillan Publishing,Co.1981.10-13.
(编辑杜昌)
——兼评专利法第九条

