考虑应力敏感性的产能与压差非线性关系

李根，李云鹏，曲炳昌，黄磊，黄建廷，常涛

（1.中海石油（中国）有限公司天津分公司，天津 300452；2.中国石油大港油田分公司勘探开发研究院，天津 300280）

考虑应力敏感性的产能与压差非线性关系

李根1，李云鹏2，曲炳昌1，黄磊1，黄建廷1，常涛1

（1.中海石油（中国）有限公司天津分公司，天津 300452；2.中国石油大港油田分公司勘探开发研究院，天津 300280）

将岩石应力敏感性代入裘比公式得到新的单井产能计算式，采用同类项消除法，将计算式变形为可由提液前后的压力数据得到提液前后产能比的计算式。将产能比的计算值与实际值代入平方误差函数作为衡量二者接近程度的手段，若改变应力敏感系数对二者接近程度影响很大，则说明应力敏感为该油田产能与压差非线性关系的主要影响因素，同时还能够得到使平方误差函数达到最小的应力敏感系数。采用该方法对埕北油田提液井的产能变化进行了分析，结果表明：高渗透油藏产能同样受制于岩石应力敏感性，得到最优化应力敏感系数后能进一步得到该油田岩心的应力敏感性曲线。

拟合法；应力敏感性；产能；提液；最优逼近

0 引言

油田开发后期高含水阶段，海上油田通常采用提液的方式进行增产。但提液井往往达不到设计产能，最突出的表现就是产能与压差不能够呈线性关系。埕北油田位于渤海油田西部海域，为典型的处于中后期开发阶段的海上油田，该油田把提液作为增产的方式是比较合理的。统计该油田提液井措施前后的采液指数后发现，提液井普遍存在液量“提不起来”的现象。

影响产能的因素很多，如表皮系数增长、岩石渗透率变化等，然而埕北油田在提液前均实施了有机解堵措施，所以表皮系数影响不大，本文重点关注渗流孔道渗透率随压差的变化。

提液前后井底流压变化较大，因此岩石所受应力变化也较大，该变化对渗流孔道的渗透率影响不可忽略，而这种渗透率的变化会影响产能。目前对于岩石应力敏感性的研究都集中在低渗油藏中［1-9］，对于高渗油藏研究较少。有观点认为高渗油藏也具有较高的应力敏感性，因为大多数渗透率敏感性测试实验都是在极高围压条件下进行的，该实验条件降低了高渗透岩心的应力敏感性［10-11］。本文认为，高渗岩心孔隙结构更为疏松，岩心骨架数量低于低渗岩心，而实验岩心都很小，且刚性结构夹持器不会变形，无法实现岩心各个位置的围压一致，这些都会造成误差。

目前，比较具有代表性的考虑渗透率的产能计算方法，有李传亮的考虑岩石渗透率对应力敏感的方法和刘峰的考虑孔隙度与渗透率双重因素对应力敏感的方法［12-14］。笔者通过计算机对其理论进行实现后发现，刘峰在后期推导过程中，对高斯误差函数进行截断时出现了错误。本文选用了综合考虑渗透率和孔隙度双重因素影响的理论，建立了一套拟合方法，通过将生产数据代入拟合式进行相关性分析，判断产能是否受到岩石应力敏感性的影响。

1 公式推导与论证

目前对考虑岩石应力敏感性产能公式的推导已经成熟，采用的方式都是将渗透率表示为压力的表达式，最后代入达西公式求得。考虑孔隙度与渗透率随应力变化的产能公式中，以文献［14］中的公式最具有代表性，其渗透率与压力的关系式见式（1），产能公式见式（2）。 文献［14］对式（2）右侧的定积分进行了进一步求解，将其变为包含高斯误差函数的形式，误差函数内变量表达式见式（3）。

文献［14］应用了误差函数的展开式（见式（4）），只截取了第1项进行简化处理。

但文献［14］中 y 的值域并非（0，1）区间，y 值在运算过程中具有绝对值大于1的情况，而对高斯误差函数简化处理的要求是其变量的绝对值不能大于1。选取文献［14］中参数（见表 1，其中 pwf的步长为 4 MPa），y值对各参数的敏感性如图1所示，y值绝对值基本都在大于1的区间内，因此该文献简化处理不成立。

表1 文献［14］中计算y值所用参数

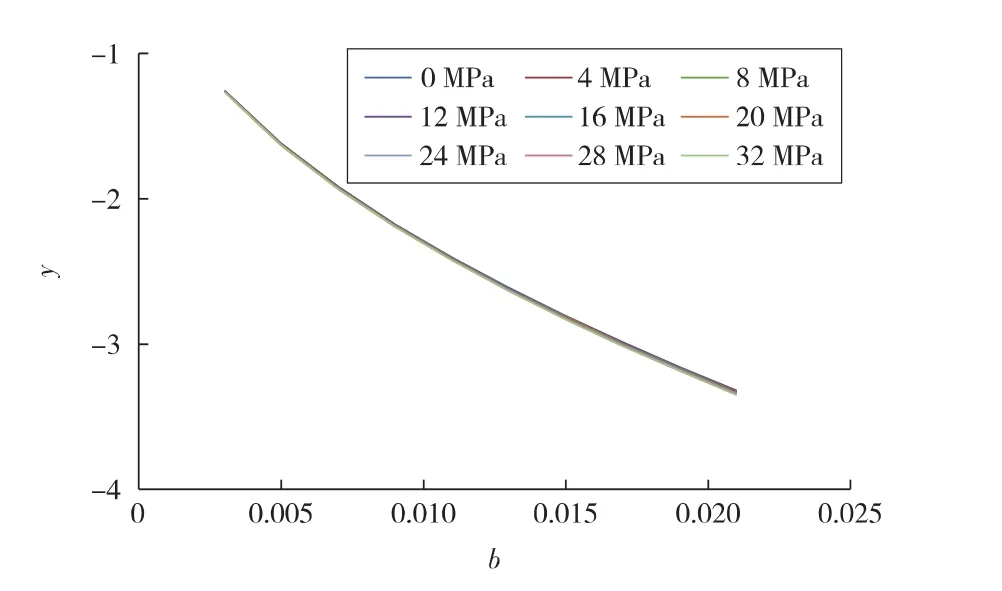
图1 不同井底流压下y值与b值的关系

本文选用式（2）作为拟合式，但未对其等号右侧部分进行简化处理，而是采用了数值积分法对定积分项进行运算。对式（2）等号左侧进行定积分处理后，得到考虑岩石敏感性的产能计算式：

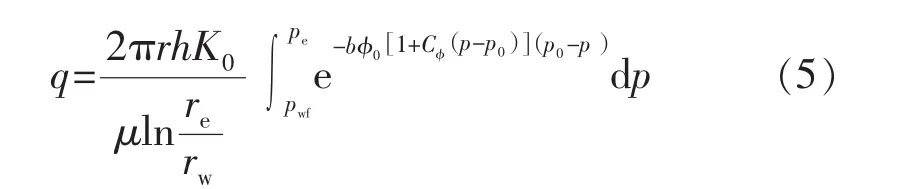
选用表2中的参数，将本文的数值积分法、文献［14］中的简化式及文献［13］中的不考虑孔隙体积变化的推导式进行编程计算，对比三者产能与压差的关系，结果见图2。

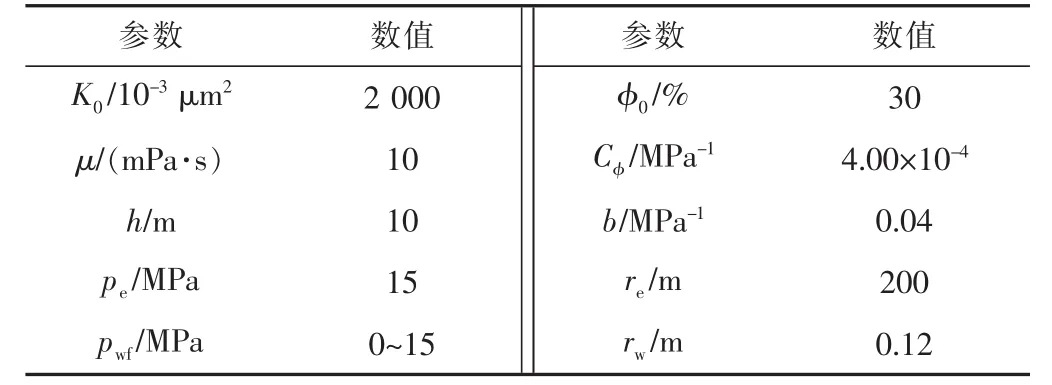
表2 3种方法敏感性分析参数

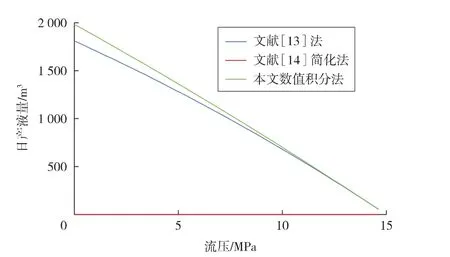
图2 3种方法的产量与井底流压的关系

由图2可以看出：此时产能与压差不再呈线性关系，且文献［14］的简化式结果显然是不合理的；同时，孔隙体积敏感性在流压低 （即生产压差大）时偏差较大，随着流压升高，孔隙体积产生的应力敏感性对产能的影响减弱。

2 拟合式方法建立

提液措施前后，式（5）等号右侧积分号前面的表达式取值是一致的。若假设提液前后的产能分别为qi，qi+1，提液前后的井底流压分别为pwfi，pwfi+1，将措施前后的产能相除，可以得到：

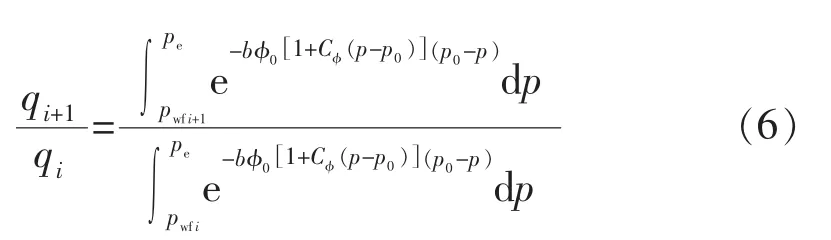
分别以符号qRCal及IPr代替式 （6）左右两侧表达式，则得到：

如果给定一组参数 pe，pwfi，pwfi+1，b，Cφ，就可计算出相应的qRCal值。

若将qRCal作为近似值处理，将提液前后实测的产液量的比值（qRObs）作为实测值处理，代入加权平方误差函数［15］，可得：

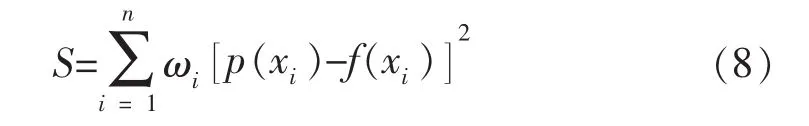
对于权重系数ωi的取值，可根据每口井在油田中的产量贡献比例或其是否具有代表性来决定。本文取ωi=1，得到：

一般情况下，对同一研究区域而言，b与Cφ可采用统一值，在给定b与Cφ的情况下，将每口提液井提液前后的产液量及 pe，pwfi，pwfi+1参数代入式（9）可计算出S。

通常情况下，Cφ取值的数量级为10-4。从式（5）可以看出，Cφ对q的影响程度远远弱于b，因此在拟合中，若Cφ为控制提液措施前后产量非线性的主要因素，则通过改变b值，S将会随之发生变化，且会存在某一b值，使得S最小。记录该b值，将该b值与Cφ的数值代入式（7），此时式（7）称为 qRObs（k）的最优逼近函数，计算出qRCal与qRObs形成的散点与y=x直线的接近程度最高。

3 实例应用

以渤海埕北油田为例。该油田主要发育一套油层，属于强边水层状油藏，渗透率为1 300×10-3～1 700×10-3μm2， 原油黏度 57 mPa·s， 其静态参数 Cφ=4.0×10-4MPa-1，φ0=30%，pe=15.6 MPa。 9口提液井措施前后动态数据见表3。

表3 埕北油田提液前后井单井动态数据

在区间［0，1.5］内对b值进行扫描，S与b之间的变化关系见图3。以二分法求得当b=0.791时S最小，S=0.35。将b值代入式（6）得到qRCal的数据组，由实测值组成qRObs的数据组，对比2组数据（见图4），可看出计算值与实测值的比值分布在直线y=1附近。

图3 S随b的变化

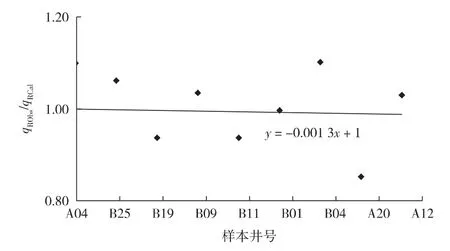
图4 不同样品实际产能比与计算产能比的关系

将b值与静态参数代入式（1），得到埕北油田地下储层渗透率随压降变化的趋势（见图5）。

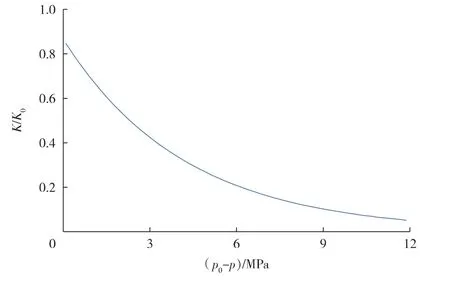
图5 埕北油田储层渗透率随压降变化的趋势

埕北油田为高渗油田，其平均渗透率高达1 670×10-3μm2。从该油田的实例应用可以看出，通过改变考虑应力敏感性产能的应力敏感参数，能够大大改善提液前后产能的拟合度。这也从一个侧面证明，高渗透率岩心的应力敏感性是不能忽视的。

4 结论

1）对比了考虑渗透率随岩石的应力敏感性变化的产能公式之间的差异，证明岩石孔隙度的应力敏感性对产能计算的影响不大。

2）对于类似埕北油田采用提液作为提高产能手段的油田而言，可通过对已经完成提液措施的井进行拟合求得最佳的b值，将其代入产能公式，进而求解需要进行提液措施井的产能。

3）在对公式简化处理时，须考虑参数取值是否在可进行简化的范围内，否则将会造成重大误差。

5 符号注释

q 为产液量，m3/s；μ 为流体黏度，mPa·s；h 地层为厚度，m；re为边界距离井底距离，m；rw为井筒半径，m；p0为测定岩心渗透率的参考压力，MPa；K为目前岩心渗透率，μm2；K0为压力 p0下的岩心渗透率，μm2；φ0为p0下的岩心孔隙度，%；Cφ为岩石压缩系数，MPa-1；pe为测边界处地层压力，MPa；p为目前地层压力，MPa；pwf为井底流压，MPa；b为渗透率应力敏感系数，MPa-1。

［1］ 武志德，周宏伟，丁靖洋，等.不同渗透压力下盐岩的渗透率测试研究［J］.岩石力学与工程学报，2012，31（增刊 2）：3740-3746.

［2］ 高博禹，周涌沂，彭仕宓.储层孔隙度应力敏感性研究［J］.石油实验地质，2005，27（2）：197-202.

［3］ 兰林，康毅力，陈一健.储层应力敏感性评价实验方法与评价指标探讨［J］.钻井液与完井液，2005，22（3）：1-4.

［4］ 李大奇，康毅力，游利军.碳酸盐岩储层渗透率应力敏感性实验研究［J］.天然气地球科学，2014，25（3）：409-413.

［5］ 战沙，戚林河，张园春，等.致密砂岩储层孔隙度渗透率随净上覆压力变化规律研究［J］.复杂油气藏，2015，8（2）：53-56.

［6］ 杨朝蓬，高树生，郭立辉，等.致密砂岩气藏应力敏感性及其对产能的影响［J］.钻采工艺，2013，36（2）：58-61.

［7］ 谢一婷，陈朝晖.疏松砂岩气藏渗透率敏感性实验研究［J］.断块油气田，2013，20（4）：488-491.

［8］ 李明军，杜建芬，卞小强.低渗透油藏应力敏感性实验研究［J］.断块油气田，2008，15（4）：97-98.

［9］ 肖曾利，蒲春生，秦文龙.低渗砂岩油藏压力敏感性实验［J］.断块油气田，2008，15（2）：47-48.

［10］李闽，肖文联，赵春兰，等.不能用净应力评价低渗砂岩岩石应力敏感性［J］.西南石油大学学报（自然科学版），2009，31（5）：183-186.

［11］ 刘晓旭，胡勇，朱斌，等.储层应力敏感性影响因素研究［J］.特种油气藏，2006，13（3）：18-21.

［12］ 李传亮，杨学锋.低渗透储集层油藏的产能特征分析［J］.新疆石油地质，2006，27（5）：567-568.

［13］ 李传亮.应力敏感对油井产能的影响［J］.西南石油大学学报（自然科学版），2009，31（2）：170-172.

［14］刘峰，王裕亮，陈小凡，等.考虑应力敏感性的低渗透油藏油井产能分析［J］.石油与天然气地质，2013，34（1）：124-128.

［15］ 西安交通大学高等数学教研室.复变函数［M］.4版.北京：高等教育出版社，2006：90-92.

（编辑 史晓贞）

Nonlinear relationship between production capacity and differential pressure based on stress sensitivity

LI Gen1,LI Yunpeng2,QU Bingchang1,HUANG Lei1,HUANG Jianting1,CHANG Tao1
(1.Tianjin Branch of CNOOC Ltd.,Tanggu 300452,China;2.Research Institute of Exploration and Development,PetroChina,Dagang Oilfield Company,Dagang 300280,China)

New calculation formula of well productivity was deduced by substituting the stress sensitivity of rock in Dupuit formula.Using the similar elimination method,the formula was transformed to a new one which makes the user get the productivity ratio from the pressure data corresponding to the pre-after liquid production.Taking the calculated productivity ratio and the actual one into the square error function to calculate the degree of the approximation,if the change of stress sensitivity coefficient has a great influence on the degree of approximation,it is proved that the stress sensitivity is the main factor affecting the nonlinear relationship between productivity and differential pressure in this oil field.At the same time,the stress sensitivity coefficient which minimizes the square error function can be obtained.Using this method to analyze the productivity change in the wells with liquid production increasing in Chengbei Oilfield,the results show that the productivity of high permeability reservoir is also controlled by the rock stress sensitivity,and the stress sensitivity curve of the core can be further obtained after calculating the optimized stress sensitivity coefficient.

fitting process;stress sensitivity;productivity;liquid enhancement;optimized approximation

TE32

A

国家科技重大专项“海上稠油高效开发示范工程”（2016ZX05058）

10.6056/dkyqt201704020

2017-01-27；改回日期：2017-05-15。

李根，男，1985年生，工程师，硕士，主要从事油藏工程研究工作。 E-mail：ligen2@cnooc.com.cn。

李根，李云鹏，曲炳昌，等.考虑应力敏感性的产能与压差非线性关系［J］.断块油气田，2017，24（4）：525-528.

LI Gen，LI Yunpeng，QU Bingchang，et al.Nonlinear relationship between production capacity and differential pressure based on stress sensitivity［J］.Fault-Block Oil&Gas Field，2017，24（4）：525-528.