优化的新陈代谢GM(1，1)模型在基坑变形监测中的应用

江宝锋 钱传俊 杨 剑

(长江水利委员会水文局长江口水文水资源勘测局,上海 200136)

优化的新陈代谢GM(1，1)模型在基坑变形监测中的应用

江宝锋 钱传俊 杨 剑

(长江水利委员会水文局长江口水文水资源勘测局,上海 200136)

针对传统的GM(1，1)模型确定积分常数C缺乏一定理论依据的问题，依据建模方差最小原则优化传统GM(1,1)模型的初始值，融合新陈代谢和新信息优先建模的思想，建立基于优化初始值的新陈代谢GM(1，1)模型，并将其应用到基坑变形监测中。结果表明，优化初始值的新陈代谢GM(1,1)模型预报精度优于传统的GM(1,1)模型、新陈代谢GM(1，1)模型和优化初始值的GM(1,1)模型。

GM(1，1)模型；基坑变形；变形监测

随着城市化进程的加快，大型基坑工程越来越多，而基坑的施工会给周边的建筑物带来安全隐患，因此对基坑进行实时变形监测，分析处理实测数据并进行变形预报具有重要意义。如何根据已测沉降数据建立科学、合理的预测模型，是当前测绘工作者研究的热点之一。

GM(1,1)是目前应用最广泛的模型，研究的是贫信息建模，对处理趋势性变形和小子样监测离散数据具有独特优势[1-2]，但是预测精度随时间的推移会越来越低，实用性有待提高。鉴于传统的GM(1,1)模型通常以第一点作为初始值来确定白化权函数中的常数C，但缺乏一定的理论依据，本文基于最小二乘约束的初始条件选取GM(1,1)模型的初始值，在预测过程中降低原点误差，同时融合新陈代谢和新信息优先建模的思想，建立基于此优化值的新陈代谢GM(1,1)模型，从而有效提高预测精度。

1 数学模型建立

设观测原始序列：

(1)

对x(0)作一次累加生成得到一个生成序列

(2)

对此建立一阶微分方程

(3)

式中，a和u是灰参数，通过最小二乘估计可得

(4)

式中，

(5)

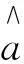
(6)

式中，C为常数，需要由初始值来确定[1-2]，通常确定白化权函数中常数C的方法理论依据不足，因此根据建模方差的概念，定义用于建模的数据资料与建模后所生成数据资料的真误差平方和数学期望[3-4]，记为δ2。根据定义有

(7)

在δ2为最小的限定条件下，对C求偏导，并另

所以常数C的值

(8)

把式(8)代入式(7)并还原预测，即可得到优化的GM(1，1)模型。

(9)

(k=1,2，…，N)

模型的精度用后验差方法检验[2]。设由已优化初始值的GM(1，1)模型得到

(10)

计算残差

(11)

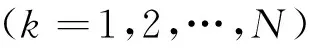
(12)

(13)

式中，

(14)

然后计算后验差比值

(15)

和小误差概率

(16)

表1列出了根据C、P取值的模型精度等级。 模型精度等级为max{P所在的级别，C所在的级别}。

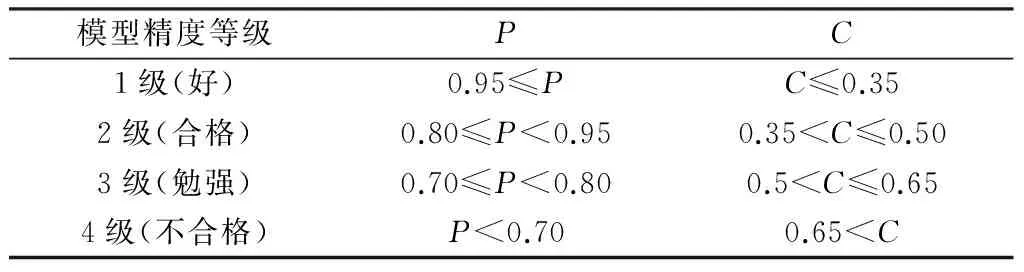
表1 模型精度等级

随着时间的推移，系统状态随着干扰系统的因素变化而变化[5-6]。即使仍采用已优化初始值的GM(1，1)模型，不仅模型的预测精度不断降低，且其预测可靠度也在下降。要避免模型精度的损失，就要尽量利用最新已知或灰色信息来淡化灰平面的灰度，因此及时引入了新的已知或灰色信息，淘汰作用弱的信息，正确反应系统状态[7]。

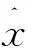
2 案例分析

本文以山东省聊城市公交集团调度中心施工基坑1号和10号监测点的监测数据为例进行模型分析。该基坑周围有居民楼和办公用楼，在基坑施工期间布设18个监测点，点编号1～18 。每期观测时间间隔为1 d。表2为1号和10号监测点的部分沉降观测数据。

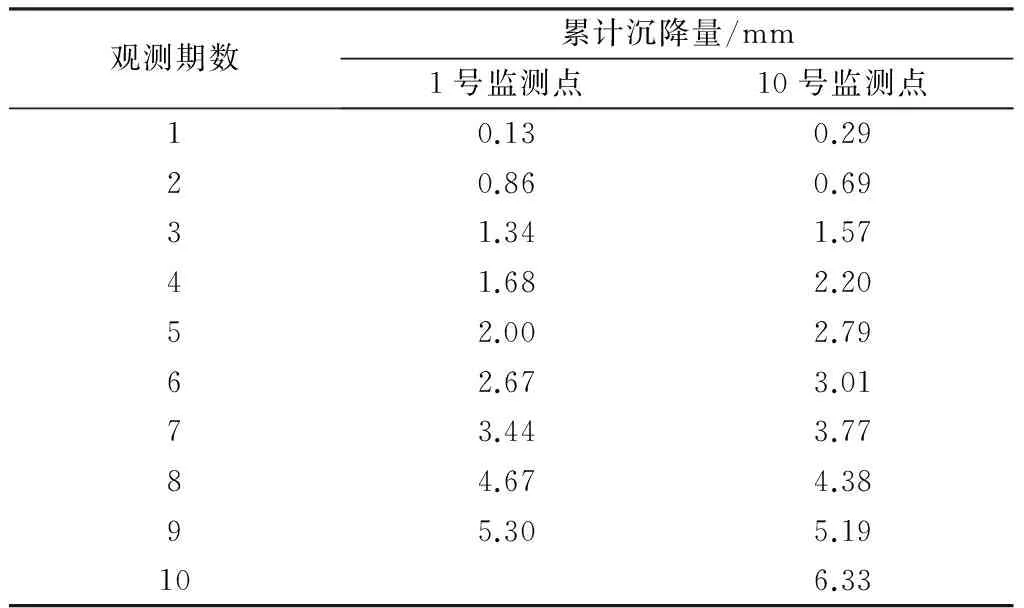
表2 1号和10号监测点的部分沉降观测数据

据此分别建立4种模型，比较其预测效果。

(1) 模型1：GM(1,1)模型；

(2) 模型2：新陈代谢GM(1,1)模型；

(3) 模型3：优化初始值的GM(1,1)模型；

(4) 模型4：优化初始值的新陈代谢GM(1,1)模型。

对于1号监测点，选取1～9期观测值为原始观测数据建立模型，对10～13期进行预测；对于10号监测点，选取1～10期沉降观测数据建立模型，对11～15期进行预测。预测结果如表3,4。

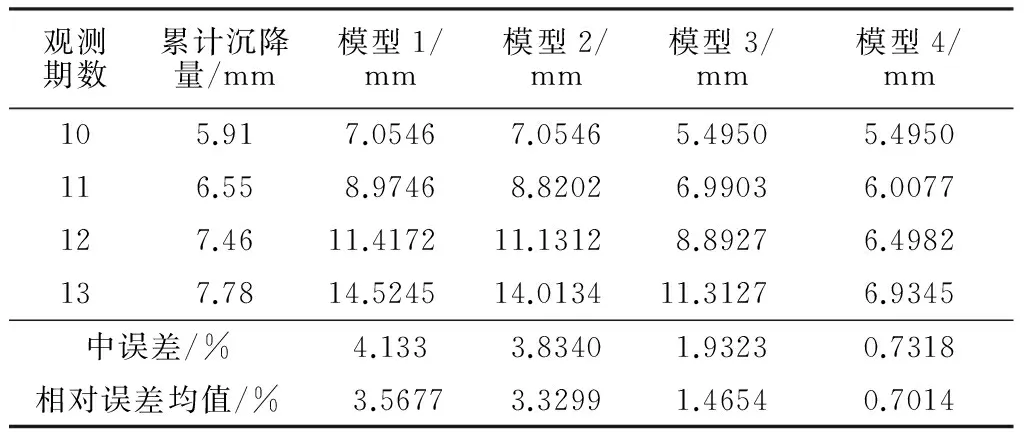
表3 4种模型预测结果及精度检验(1号监测点)

表4 4种模型预测结果及精度检验(10号监测点)

比较几种模型的预测结果，GM(1,1)模型(模型1)预测精度最低，新陈代谢GM(1,1)模型(模型2)和基于优化初始值的GM(1,1)模型(模型3)比原始灰色模型的精度都要高。但是随着时间的推移，预测的精度也越来越低。主要是因为变形没有延续前期的增长趋势。而基于优化初始值的新陈代谢模型(模型4)最优，预测值与实测值更加吻合，精度明显提高。这是因为改正积分常数C能得到模型实测值与一阶累加值的最佳拟合，且最新的数据包含了扰动因素的信息，加入到数据序列中进行预测，能更好地反映沉降变化趋势的目前特征。

3 结 语

本文构建的基于优化初始值的新陈代谢GM(1，1)模型通过改正积分常数C，消除原点误差，克服了传统GM(1,1)模型以第一点作为初始值的缺陷，同时及时补充新数据，去掉因时间推移而使信息意义降低的老信息。选取初始条件和建模过程均为动态的，符合变形系统的演化特征，所以本文构建的模型精度明显高于原始灰色模型、新陈代谢GM(1,1)模型和优化初始值的灰色系统，因此在基坑的变形监测数据分析中，应用基于优化初始值的新陈代谢GM(1,1)模型是行之有效的。

[1] 郭齐胜.系统建模原理与方法[M].长沙：国防科技大学出版社，2003.

[2] 黄声享，尹晖，蒋征.变形监测数据处理[M].武汉：武汉大学出版社，2003.

[3] 邱淑芳，王泽方.灰色GM(1，1)模型背景值计算的改进[J].知识丛林，2007(2)：129-131.

[4] 邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社，1987.

[5] 周卫.基于MATLAB的灰色系统沉降预测[J].测绘通报，2002(6)：34-36.

[6] 王利，张双成.动态灰色预测模型在大坝变形监测及预报中的应用研究.西安科技大学学报，2005,25(3):328-332.

[7] 刘棠洪. 残差灰色预测模型在地面沉降监测中的应用[J]. 城市环境与城市生态，2007，20(5)：32-34.

(编辑：唐湘茜)

2017-03-31

江宝锋，男，长江水利委员会水文局长江口水文水资源勘测局，工程师.

1006-0081(2017)06-0036-03

P258

A