基于磨光函数的权值直接确定双输入BP神经网络

杨文光，田立勤，高艳辉

(1.华北科技学院 基础部，北京东燕郊 101601；2.华北科技学院计算机学院，北京东燕郊 101601)

基于磨光函数的权值直接确定双输入BP神经网络

杨文光1，田立勤2，高艳辉1

(1.华北科技学院 基础部，北京东燕郊 101601；2.华北科技学院计算机学院，北京东燕郊 101601)

利用磨光函数与采样数据建立了双输入单输出的权值直接确定的BP神经网络。改进后的网络依据训练数据重要性，选择以数据为中心的磨光函数作为激励函数，同时网络结构可以根据数据多少得到相应的调整。根据误差反向传播学习算法得到了改进后网络的权值直接确定算法。在仿真中，利用2个不同的目标函数验证了改进算法的有效性与建模精度。实验结果表明，三次磨光函数建立的网络性能优于二次磨光函数建立的网络。

磨光函数；权值确定；结构优化；仿真

0 引言

BP神经网络自1986年问世以来，在优化计算、智能控制与人工智能方面发挥了巨大的作用。在处理相对复杂的数据过程中，传统的BP神经网络往往存在迭代寻优缓慢、易于陷入局部极值的缺陷。为了改进传统BP神经网络存在的不足，不同学者分别从激励函数、网络结构、学习算法与引入动量项等方面对BP神经网络进行了尝试改进，在学习效率、建模精度与不同应用领域取得了较好的应用结果[1-8]。然而，改进后的学习算法仍然是需要迭代寻优的，涉及的网络结构往往是固定不变的，这些设置要求仍然限制了BP神经网络的进一步发展。事情上，网络结构应该会随着训练数据的多少进行相应的调整才能体现智能性；若做到实时快速建模与逼近，网络各层间的权值应该做到直接确定，这样网络的实时性就会非常好。文献[9-11]在传统BP神经网络基础上利用极限思想将误差反向传播学习算法进行了改进得到了与之等价的权值直接确定算法，这为BP神经网络的发展提供了新的研究思路。文献[12,13]在研究模糊系统的基础上，充分考虑了训练数据的重要性，以训练数据中的部分数据作为生成隶属函数的源数据，给网络结构赋予了动态可调的特性，丰富和发展了权值直接确定算法。

文献[13]研究了样条函数在BP神经网络中的权值与结构确定算法，网络结构可以进行与训练数据一致的调整，获得了较高的建模精度，但考虑到由三次样条函数构造的乘积型激励函数的复杂性与数据空间分布的简易性需求，本文将在磨光函数基础上进行网络的进一步改进与简化。

1 权值直接确定神经网络

磨光函数是适应曲线的光滑拟合逼近要求产生的，它具有足够的光滑性、保凹凸性，是一种构造相对简单、逼近性能相对较好的函数。在神经网络的构造过程中，激励函数、网络结构与学习算法是神经网络构成的三大要素。鉴于磨光函数的优良特性，下面将利用磨光函数与训练数据进行有机的结合，进行权值直接确定神经网络的拓展与丰富。充分考虑训练数据的重要性，依靠数据

与磨光函数生成激励函数，利用逼近误差函数进行网络结构的权值直接确定优化。

1.1 磨光函数与激励函数

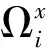
(1)

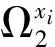
图1 三次磨光函数

(2)

(3)

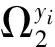
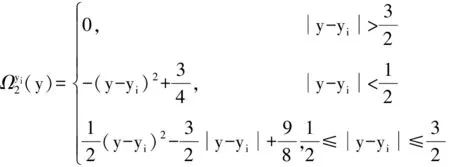
(4)

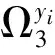
(5)

1.2 网络结构与权值确定

采用简化的含有输入层、隐含层与输出层的三层BP神经网络，其基本网络结构如图2所示，输入层到隐含层的权值设置为1，设隐含层到输出层的权值向量为w=[w1,w2,…,wl]T，其中l0=m0·n0，m0表示从m个x数据中提取的部分数据，n0表示从n个y数据中提取的部分数据。传统的BP神经网络是利用误差反向传播学习算法结合训练数据不断优化权值向量w的，由于涉及多个权值与多次迭代，因此存在迭代寻优效果不理想的问题。在网络的训练建立过程中，被选择出来的l组数据充当了网络构建一组基，通过寻找恰当的权值来表示其他数据，所以与图2对应的三层BP神经网络可以表示为：

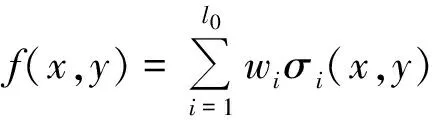
(6)

其中，若第i个激励函数σi(x,y)是按照下式生成的：

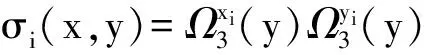
(7)

则称公式(6)为基于三次磨光函数生成的BP神经网络。若第i个激励函数σi(x,y)选择下式形式：

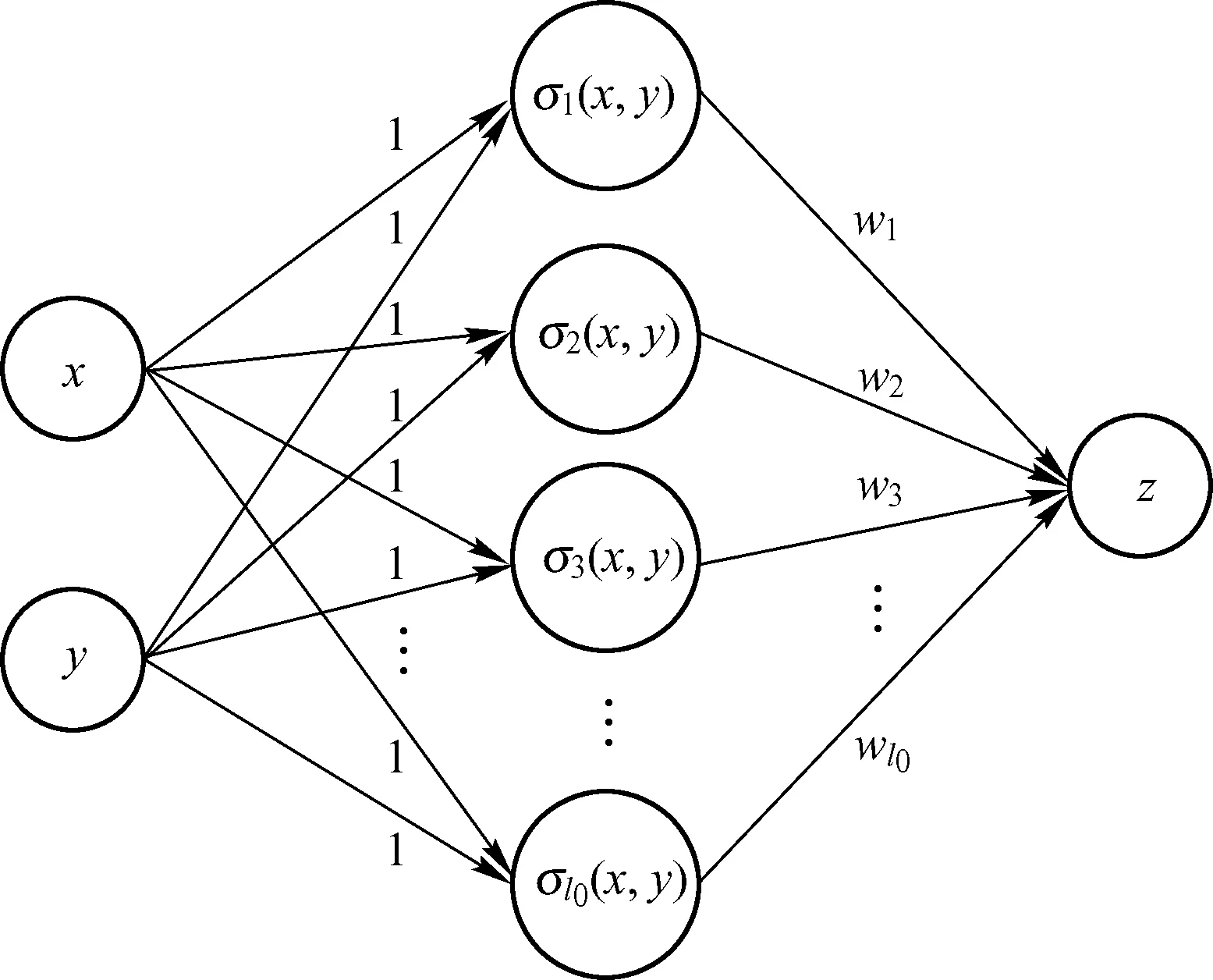
图2 双输入单输出BP神经网络

(8)

则称公式(6)为基于二次磨光函数生成的BP神经网络。

定义1[15]设X∈Rn×m，如果存在矩阵Y∈Rm×n，使得下列等式成立：

XYX=X,YXY=Y,(XY)T=XY,(YX)T=YX

则称Y为X的广义逆矩阵(伪逆)，记作Y=X+。

下面从l组训练数据(x1,y1,z11),…,(xi,yj,zij),…,(xm,yn,zmn)中选取l0组数据作为构造隐含层激励函数的源数据(l≥l0)，利用极限思想改进BP学习算法可得权值直接确定算法。

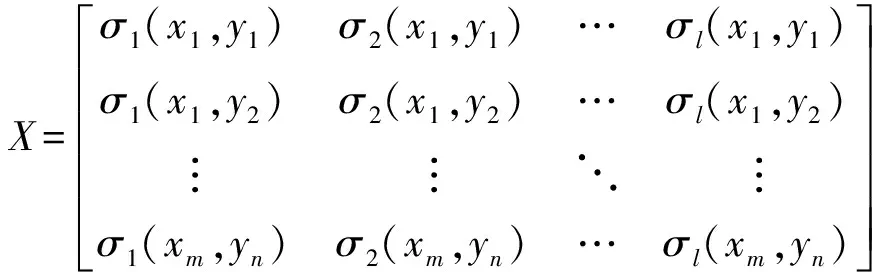
w=(XTX)-1XTZ.

(9)

证明：根据误差反向传播学习算法，需要定义误差函数

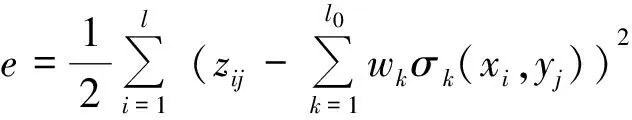
(10)

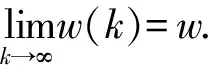
(11)

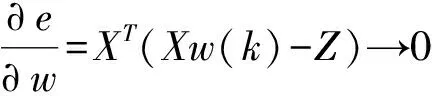
2 仿真验证

下面将使用配置为Intel(R)Core(TM)i5-2450M CPU 4.00GB内存 64位操作系统的宏基笔记本进行相关的仿真实验，选用的MATLAB软件版本为7.5.0(R2007b)。选择2个不同的目标函数分别进行磨光函数为二次与三次的建模实验，检验基于采样数据、磨光函数与权值直接确定算法的建模效果。设定输入变量x∈[0,1]，输入变量y∈[0,1]。

目标函数1：z=xy

目标函数2：z=ysin(x+y)exp(-y2)+1

以上仿真实验中，训练数据按照等间距从[0,1]×[0,1]中选取，步长为0.02，而隐含层神经元激励函数的构造数据则按照步长为0.1从[0,1]×[0,1]中选取，以此检验训练数据的逼近误差，从图4与图6可以发现，三次磨光函数生成的网络逼近精度优于二次磨光函数生成的网络。用于网络结构的构造数据远远少于训练数据，当增加网络结构的构造数据时，网络的逼近精度将会进一步提高，在满足误差逼近精度要求的情况下，可以灵活选择构造网络的数据数目，简化了网络的设计。

图3 目标函数1与三次磨光函数逼近模型

3 结论

作为应用较为广泛的BP神经网络，为了提高网络的逼近性就需要在网络结构与学习算法方面进行深入的研究。本文首先选择二次与三次磨光函数作为BP神经网络的激励函数，利用训练数据对激励函数进行改写，使得隐含层神经元个数可以按照设计要求进行动态调整。然后，利用极限思想推导得到了特定隐含层激励函数与训练数据结合下的权值直接确定算法。最后，将所设计的改进BP神经网络用于双输入单输出系统的建模中，仿真结果检验了所提方法的有效性。这将为进一步开展应用研究提供可以借鉴的研究思路。

图4 l>l0时三次与二次建模误差

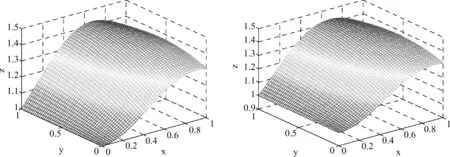
图5 目标函数2与三次磨光函数逼近模型

图6 l>l0时三次与二次建模误差

[1] 刘刚.一种综合改进的BP神经网络及其实现[J].武汉理工大学学报,2002,24(10):57-60.

[2] 王卓，王艳辉，贾利民，等.改进的BP神经网络在铁路客运量时间序列预测中的应用[J].中国铁道科学,2005,26(2):127-131.

[3] 王美玲，王念平，李晓.BP神经网络算法的改进及应用[J].计算机工程与应用,2009,45(3):47-48.

[4] 虞文胜.基于改进BP神经网络的航空液压油软测量[J].计算机测量与控制,2016,24(3):21-24.

[5] 李泽秀，朱昱，鲜勇，等.弹道导弹飞行时间的BP神经网络控制方法[J].飞行力学,2017,35(2):54-58.

[6] 刘文雅，潘洁.基于神经网络的马尾松叶绿素含量高光谱估算模型[J].应用生态学报,2017,28(4):1128-1136.

[7] 陈海燕，戎晓力，林阳.矿区开采沉陷预计的改进BP神经网络模型[J].金属矿山,2017,490:119-122.

[8] 张宪红，张春蕊.一种改进的细胞神经网络图像边缘提取方法[J].暨南大学学报(自然科学与医学版),2017,38(2):178-184.

[9] 张雨浓，劳稳超，余晓填，等.两输入幂激励前向神经网络权值与结构确定[J].计算机工程与应用,2012,48(15):102-106.

[10] 张雨浓，曲璐，陈俊维，等.多输入Sigmoid激励函数神经网络权值与结构确定法[J].计算机应用研究,2012,29(11):4113-4151.

[11] 肖秀春，张雨浓，姜孝华.MISO多元广义多项式神经网络及其权值直接求解[J].中山大学学报(自然科学版)，2009，48(4):42-56.

[12] 杨文光，闫守峰，文小艳.双输入型模糊前向神经网络的构建[J].湖南师范大学自然科学学报,2013,36(3):33-38.

[13] 杨文光，钟云香，李强丽，等.双输入样条神经网络权值与结构确定算法[J].中山大学学报(自然科学版),2014,53(3):61-66.

[14] 朱长青.数值计算方法及其应用[M].北京：科学出版社，2006.

[15] 史荣昌，魏丰.矩阵分析[M].北京：北京理工大学出版社，2010.

Direct Determination of BP Neural Network with Dual-Input by Weights Based on Smoothing Function

YANG Wen-guang1,TIAN Li-qin2,GAO Yan-hui1

(1.DepartmentofBasicCurriculum,NorthChinaInstituteofScienceandTechnology,Yanjiao，101601,China; 2.SchoolofComputer,NorthChinaInstituteofScienceandTechnology,Yanjiao，101601,China)

The BP neural network with double input single output directly determined by weights，is constructed by using the smoothing function and the sampled data. Based on the importance of training data,the selected data are used as the center of the polishing function as an activation function.At the same time,the network structure can be adjusted according to the number of data.According to the error back propagation learning algorithm,the weights of the improved network are determined directly.In the simulation experiment,two different objective functions are used to verify the effectiveness of the improved algorithm and the accuracy of model.The experimental results show that the network performance established by cubic polishing function is better than that of quadratic polishing function.

smoothing function;weigh determination;structure optimization;simulation

2017-03-15

中央高校基本科研业务费(3142016023)，河北省科技计划项目(162176438)，国家自然科学基金(61472137)

杨文光(1981-)，男，河北保定人，博士，华北科技学院基础部副教授，现从事模糊系统、神经网络与智能信息处理等研究。E-mail：wenguang662003@aliyun.com.

TP183

A

1672-7169(2017)02-0107-05