基于随机共振的大频率信号相干接收误码率研究
张福佳,江 虹,张秋云
(西南科技大学信息工程学院,四川 绵阳 621010)
基于随机共振的大频率信号相干接收误码率研究
张福佳,江 虹,张秋云
(西南科技大学信息工程学院,四川 绵阳 621010)
针对信道环境恶劣条件下的大频率数字信号相干接收问题,提出了一种基于调参随机共振系统降低数字信号相干接收误码率(BER)的方法。从时域、频域及误码率三个方面对大频率二进制相移键控(BPSK)信号的随机共振相干接收方法进行了研究。首先,通过调整系数R改变非线性随机共振系统的参数a、b,将其共振频率提高R倍,从而实现大频率信号的随机共振,提高信号的信噪比(SNR);然后,对通过随机共振系统后的信号进行相干解调,并计算误码率。试验结果表明,与传统解调方法相比,该方法的误码率在低信噪比情况下有明显降低,当SNR=-14 dB时,较传统解调系统误码率可降低25.28%。随机共振系统提高了信号相干接收性能。随机共振理论在信号接收解调及信号处理等方面存在优势。
随机共振; 非线性系统; 信噪比; 相干解调; 二进制相移键控; 误码率; 信号处理
0 引言
随机共振(stochastic resonance,SR)最早是1981年由意大利学者Benzi等[1]在研究地球气候“冰川期”和“温暖期”周期交替现象时提出的。其理论[2-5]可简单理解为:噪声通过非线性系统加强了原本微弱的信号,即可利用噪声的积极作用提高系统输出信噪比。随机共振理论因其在微弱信号增强、放大和检测方面所具有的独特优势,在微弱信号检测识别[6]、电磁系统[7]、光信号处理[8]等领域得到广泛应用。近年来,为改善信息传输性能,部分学者尝试把随机共振理论应用到通信领域。例如,王爱珍等[9]为提高现有直接序列扩频通信系统接收信号的解调增益,提出了分层级联随机共振算法;尚金红等[10]提出了一种基于随机共振理论降低二进制相移键控信号相干接收误码率(bit error rate,BER)的算法,在-7.4 dB时的误码率较传统线性解调系统降低了20.1%,但只适用于低频弱信号。
为解决通用非线性随机共振系统受小频率参数限制的问题,本文通过尺度变换方法设计了适用于大频率信号的随机共振系统,并将该随机共振系统应用到二进制相移键控(binary phase shift keying,BPSK)信号相干接收系统中,实现了噪声能量向信号能量的逐步转化,提高了信号的信噪比(signal noise ratio,SNR),降低了相干接收的误码率。
1 随机共振机理
具有双势阱特性的郎之万方程是描述双稳态系统的经典模型:
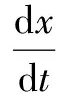
(1)
势函数U(x)的表达式如下:

(2)
所以,郎之万方程也可表示为:
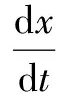
(3)
式中:a、b为大于零的双稳态系统参数;x(t)为双稳态系统的输出函数;s(t)为双稳态系统的输入函数,是含有噪声的信号。
s(t)=Asin(2πft)+η(t)
(4)
将式(4)代入式(3),可得对应的郎之万方程表达式如下:
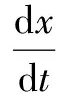
(5)
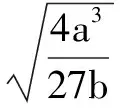
2 大频率随机共振
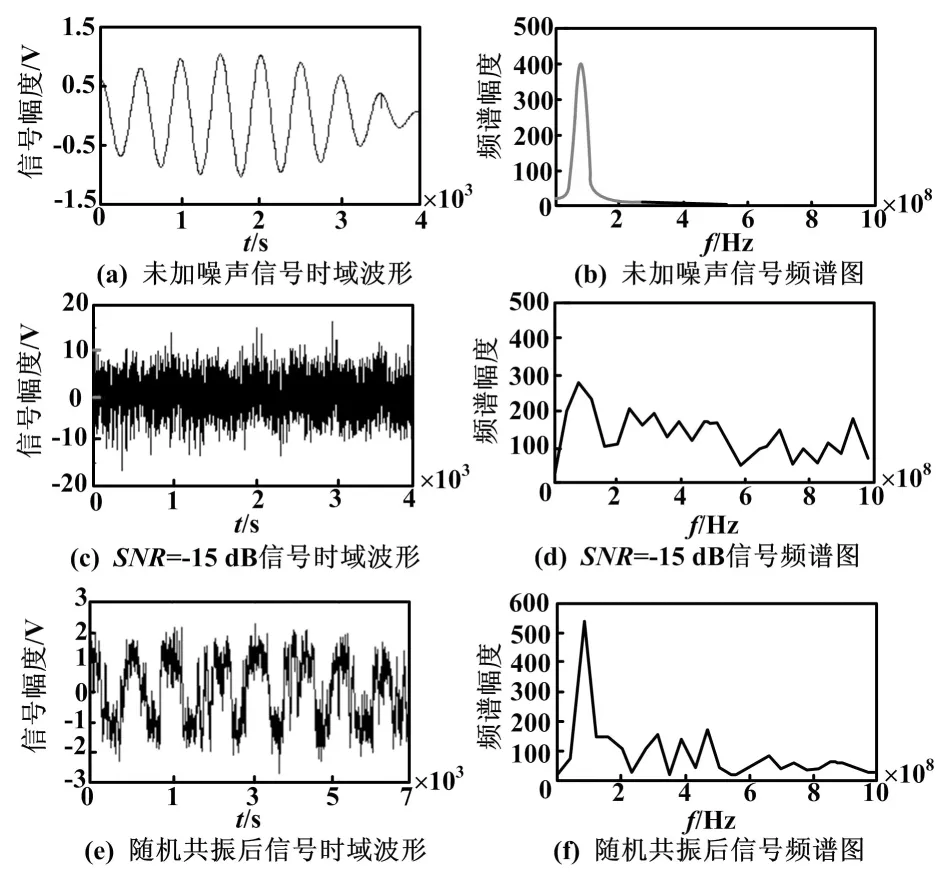
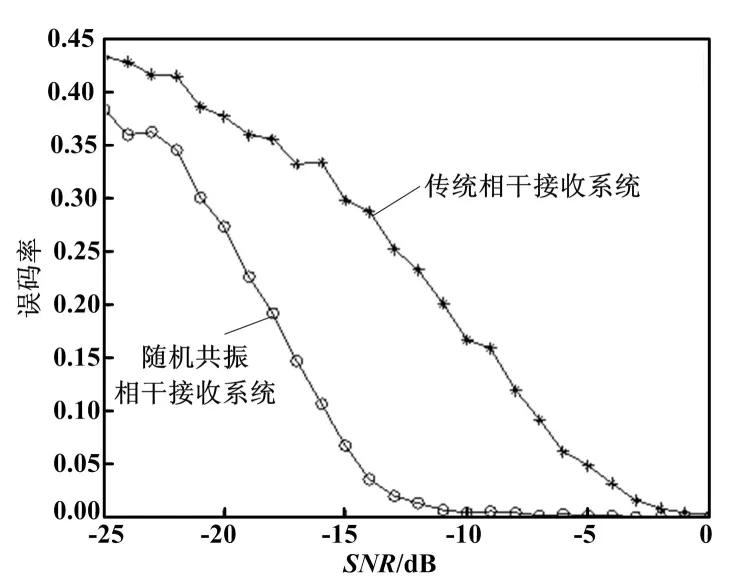
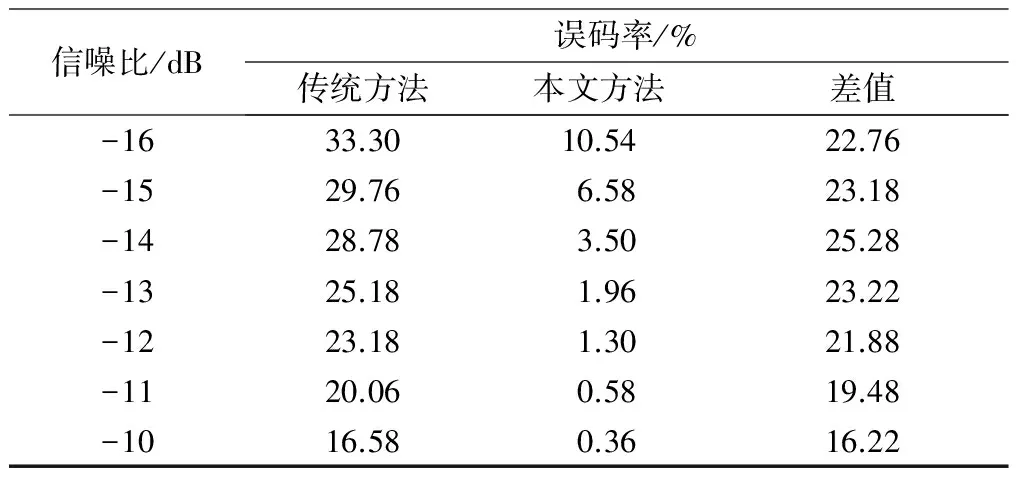
根据绝热近似理论[11-12],输入信号频率必须满足0 (6) 从Kramers逃逸率的极限值表达式可以看出,增大参数a,可以增大极限值rklim。但是随着a的增大,ΔU也会随之增大,rk将快速减小并趋于零,从而导致不能产生随机共振。若保持a不变,增大b,ΔU随之减小,rk增大,且随着b增大rk将逐步趋于极限值rklim。但是由于a和rklim不变,故仅增大b不会使rk超出rklim,也无法产生随机共振。因此,仅仅调整a或b,都不能使大频率信号产生随机共振;只有同时调整a和b,才能实现大频率信号的随机共振。以系数R作为调整因子,设式(5)中的a和b及轨道解x有如下变换: (7) (8) (9) 根据上述大频率随机共振调整原理,提出了一种基于随机共振的任意大频率数字信号相干接收方法。与传统相干接收方法相比,该方法降低了相干接收误码率,其系统模型如图1所示。 图1 随机共振相干接收系统模型图 随机共振相干接收方法思路如下。 ①调整系数R,令R=10n,且f/R∈(0,fMmax],使系统能够产生所需信号频率的随机共振,即a′=Ra、b′=R3b,代入式(9)进行非线性系统求解。 ③对信号x(t)进行相干解调和低通滤波,再抽样判断输出解调后的基带信号,并计算误码率。 4.1 大频率信号随机共振分析 对大频率信号进行随机共振分析,设输入信号幅度为A=1 V、载波频率fc=8 MHz、采样频率fs=500fc,得到的输出信号时域波形和频谱如图2所示。 图2 输出信号波形和频谱图 图2为信噪比SNR=-15 dB的BPSK信号波形和频谱图。不加噪声的信号时域波形和频谱如图2(a)、图2(b)所示,加噪后的信号时域波形和频谱如图2(c)、图2(d)所示。 由图2(a)和图2(b)可知,由于信号在通过信道时会有一定的衰减,故信号的幅度不恒为1 V;从图2(c)、图2(d)可以看出,加入噪声后,信号完全淹没在噪声中,且频谱在f=8 MHz处没有出现谱峰值。调整系数R,令R=1×109,则参数a′=Ra=1×109,参数b′=R3b=1×1027,代入式(9)求解,则非线性随机共振系统输出信号和功率谱如图2(e)、图2(f)所示。调整参数R=1×109后,非线性共振系统理论上最大可满足频率为107 4.2 相干接收误码率分析 采用MATLAB仿真平台,分别对图1所示的随机共振相干接收系统和传统相干接收系统进行了仿真。考虑到信号经过信道后会有一定衰减,在仿真过程中,加入了成形滤波,使得接收到的BPSK信号在某些时刻幅度小于1 V。设置输入信噪比为-25~0 dB,载波频率为fc=8 MHz,采样频率为fs=500fc,样本点数N=4 000,其传统相干接收系统输出误码率与随机共振相干接收系统输出误码率对比如图3所示。 图3 输出误码率对比图 从图3可以看出,随着信噪比的增加,误码率逐渐减小;当SNR<0 dB时,随机共振相干接收方法的误码率曲线明显低于传统方法的误码率曲线;当SNR=0 dB时,两种方法的误码率曲线基本重合;当SNR≥-10 dB时,随机共振相干接收系统的输出误码率趋于0。 对于随机共振相干接收系统的输出误码率曲线,可分为三个部分进行分析。 ①当-25 dB≤SNR≤-22 dB时,随机共振相干接收方法误码率相较于传统方法的误码率有所降低,但不明显。 ②当-22 dB 表1 两种方法误码率比较 从表1可以看出,当SNR=-14 dB时,误码率可降低25.28%,表明随机共振相干接收系统接收信号的准确性高于传统相干接收系统。 ③当SNR≥-10 dB时,随机共振相干接收系统的输出误码率趋于0。当信噪比SNR=-10 dB时,随机共振接收系统输出误码率为0.36%,而传统接收系统的输出误码率为16.58%。这表明随机共振相干接收系统在较强噪声环境中也可准确接收信号。 本文研究了应用随机共振技术降低大频率BPSK信号接收误码率的方法。首先,利用可调参非线性随机共振系统,使大频率数字信号产生随机共振现象,从而提高接收信号信噪比;再将该信号进行相干解调,并计算接收误码率。本文给出了随机共振相干接收系统模型,比较了传统相干接收方法和随机共振相干接收方法的误码率情况,分析了在高斯白噪声环境下噪声强度对系统误码率仿真曲线的影响。试验结果显示,随机共振相干接收系统相比传统相干接收系统对接收信号的误码率有明显降低。在信噪比为-10 dB时,误码率为0.36%,这表明随机共振相干接收系统性能较好,对其他数字接收系统具有重要的参考作用。当然,随机共振相干接收系统仍存在一些问题,如对采样频率要求较高,不利于实际信号处理,需要进一步改进和优化。 [1] BENZI R,SUTERA A, VULPIANI A.The mechanism of stochastic resonance[J].Journal of Physics A Mathematical & General,1981,14(11):453-457. [2] BENZI R,PARISI G,STUEM A.A theory of stochastic resonance in climatic change[J].SIAM Journal on Applied Mathematics,1983,43(3):565-578. [3] 冷永刚.双稳调参高频共振机理[J].物理学报,2011,60(2):77-83. [4] 梁军利,杨树元,唐志峰.基于随机共振的微弱信号检测[J].电子与信息学报,2006,28(6):1068-1072. [5] 范剑,赵文礼,张明路,等.随机共振动力学机理及其微弱信号检测方法的研究[J].物理学报,2014,63(11):111-121. [6] 樊养余,李利品,党瑞荣,等.基于随机共振的任意大频率微弱信号检测方法研究[J].仪器仪表学报,2013,34(3):566-572. [7] 王国富,张海如,张法全,等.基于尺度变换随机共振的瞬变电磁弱信号检测[J].地球物理学报,2011,54(7):1928-1934. [8] 曹广占.弱光信号的随机共振增强技术研究[D].西安:中国科学院研究生院(西安光学精密机械研究所),2014. [9] 王爱珍,侯成郭,任国凤.直接序列扩频的分层级联随机共振接收算法[J].计算机应用,2015,35(4):934-937. [10]尚金红,王辅忠,张光璐,等.基于随机共振的2PSK信号相干接收误码率的研究[J].应用声学,2015,34(6):495-500. [11]张刚,胡韬,张天骐.基于随机共振大参数微弱周期信号检测[J].科学技术与工程,2015,15(35):189-192. [12]郝静,杜太行,江春冬,等.调参随机共振在超高频微弱信号检测中的应用[J].计算机应用,2016,36(9):2374-2380. Study on the Bit Error Rate of Coherent Reception ZHANG Fujia,JIANG Hong,ZHANG Qiuyun Focusing on the coherent receiving issue of high frequency digital signals in poor channel environment,a new method based on stochastic resonance system to reduce the bit error rate (BER) of the signal is proposed.The stochastic resonance coherent reception method for BPSK signals with large frequency is studied from three aspects:time domain,frequency domain and the bit error rate.Firstly,to realize the stochastic resonance of the large frequency signal and improve the signal noise ratio(SNR) of received signals,the resonance frequency is enhanced byRtimes through adjusting the coefficientRto change the parametersaandbof the nonlinear stochastic resonance system.And then,through demodulating the signal after dealing with the stochastic resonance system,the SNR is calculated.The test results show that comparing with the traditional demodulation system,the bit error rate has significantly reduced in a low SNR environment,and it can reduce 25.28% when the input SNR equals -14 dB.The coherent reception performance is improved through the stochastic resonance system,and it shows that the stochastic resonance theory has potential advantages in signal reception demodulation and signal processing,etc. Stochastic resonance; Nonlinear system; SNR; Coherent demodulation; BPSK; Bit error rate; Signal processing 张福佳(1993—),女,在读硕士研究生,主要从事通信与信息处理的研究。E-mail:617896316@qq.com。 江虹(通信作者),男,博士,教授,博士生导师,主要从事通信与信息处理、认知无线电技术、无线组网测控技术方向的研究。 E-mail:jianghong@swust.edu.cn。 TH-3;TP311 A 10.16086/j.cnki.issn1000-0380.201707013 修改稿收到日期:2017-02-22
3 数字信号相干接收系统模型

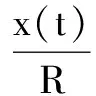
4 系统输出数值仿真与性能分析
5 结束语
of High Frequency Signal Based on Stochastic Resonance
(School of Information and Engineering,Southwest University of Science and Technology,Mianyang 621010,China)

