农产品供应链双价值超网络动态均衡分析

曹慧英+何亚辉+彭若愚+李昌兵

摘要：考虑经济价值和信誉价值，构建由农产品生产商、分销商和零售商构成的农产品供应链双价值超网络模型，利用变分不等式描述不同决策者的独立行为以及决策者之间相互影响的竞争行为，确定供应链每层竞争成员达到均衡以及整个超网络系统达到动态均衡的条件，在此基础上，利用改进的投影梯度算法确定农产品交易中合理的冷链水平和交易量，以此促进物流在供应链成员间的有效性流动，降低整个供应链系统的不确定性，为提高整个农产品供应链网络的利益均衡与长期稳定发展提供科学的分析依据。

关键词：冷链水平；超网络；变分不等式；双价值；动态均衡

中图分类号： F252.2文献标志码： A

文章编号：1002-1302（2017）10-0291-05

长期以来，我国的农产品在从生产者至消费者过程中，腐损率严重，果蔬产品的腐损率达到20%～30%，带来的损失每年近4 807万t，而发达国家农产品的腐损率却低于5%，造成这种现象的主要原因是较低的农产品冷链流通率。目前，我国农产品的冷链流通率为10%左右，远低于发达国家。2013年2月7日，国务院发布了《关于落实中共中央国务院关于加快发展现代农业进一步增强农村发展活力若干意见有关政策措施分工的通知》，其中，多项政策涉及农产品的冷链物流问题，这表示农产品供应链的冷链交易受到重视。与此同时，各个电商和传统物流企业开始加速布局农产品的冷链物流，2013年，菜鸟物流牵手郑明物流打造冷链物流平台，顺丰优选启动华东华南冷链物流布局，京东冷链物流业也开始生鲜和农产品的冷链配送布局，故农产品供应链的冷链交易研究对我国农产品的安全效益和经济效益具有重要的现实意义。

对于农产品供应链的冷链物流研究，冷志杰等建立了农产品供应链四维网络模型，并对其进行了分析[1]。赵霞等利用混合粒子群算法来优化农产品网络模型[2]。但斌等针对农产品供应链网络的整链协调问题，考虑价值损耗条件下，集中决策是否有效的研究[3]。廖莉在农产品供应链分销网络中考虑了变质率、服务水平等因素，并对其进行了优化研究[4]。黄纯辉则研究了食品冷链单链与跨链网络的优化问题[5]。

以上大多研究农产品供应链企业的经济价值，忽视了农产品交易中相对重要的信誉价值，有些电商物流企业甚至牺牲其前期的经济利益而追求信誉价值最大化，以便占领市场实现最终盈利，对于鲜活度直接影响销售水平和顾客满意度、忠诚度的产品，企业的信誉价值更是其长期追求的目标。以上大部分研究也忽视了农产品供应链中各个企业的具体目标价值，更多的是从整链或者单个链点企业的利润最大化来研究，而实际中各个企业都是追求其自身价值最大化。本研究首先选以超网络模型来分析农产品供应链中各个企业追求的经济价值和信誉价值最大化，构建了存在内在逻辑关联的经济价值网络和信誉价值网络，对各个企业进行2个网络的分析，并给出最终的网络均衡理论。

考虑冷链水平和合理的交易量对农产品供应链中各个企业总价值的影响，对于农产品供应链中的企业而言，冷链水平的提高一方面意味着其配送成本和固定成本的提高，针对城郊或城市内短途农产品配送，非冷链配送不会影响农产品的外观，故不影响其交货，但会影响农产品的保质期，另一方面，冷链水平的提高意味着产品高鲜活度带来的信誉价值提高，合理的冷链水平和交易量是影响农产品供应链企业价值最大化的重要因素。

1双价值超网络模型的构建与供应链各成员行为分析

1.1超网络简介

美国学者Nagurney等提出，考虑供应链网络中各层成员的各自行为与其他成员决策的相互影响，建立一个网络均衡模型，第一次提出超网络的概念[6]。超网络作为一种可以有效解决多层次多目标且具有联系的复杂系统的工具，在计算机[7]、组织知识分析[8]、价格决策[9]、电力[10]、生态[11]、运输[12]等领域得到了广泛应用。王众托院士将超网络概念引入中国，并指出了超网络是具有多层性、多属性、多准则的“高于而又超于现存网络”的一种网络[13]。浠玉虎等对超网络的基本概念、特点和常见模型进行了总结和探讨，给出了超网络均衡的一般解法[14]。

1.2双价值农产品供应链超网络模型的构建

本研究构建的农产品供应链双价值超网络模型（图1），由经济价值网络和信誉价值网络组成，经济价值网络即实际农产品供应链带来的经济收益，与之相应是在农产品交易时所同时产生的信誉价值网络；每个网络都包括3层网络结构，第一层代表生产商集合，第二层代表分销商集合，第三层代表零售商集合，同层之间的虚线表示相关影响关系，是一种竞合关系，各分层之间的实线代表非冷链运输方式，虚线代表冷链运输方式。

[FL（2K2]由于交易过程中的各个企业的交易是一个相互影响、相互交织的整体系统，上游企业和下游企业的交易量和冷链水平会继续对下游企业与更下一级企业的交易造成影响。另一方面，对于理性的企业，经济价值是其追求的目标，在面临市场竞争时，又会注重其信誉的高低，即其信誉价值。考虑各层之间和各个企业价值之间的协调，应用超网络能求得整体供应链的流量均衡和价值均衡的特征，构建超网络模型，能保证整个供应链中各层企业之间交易量协调和冷链水平的协调。

模型满足以下假设：H1：农产品在生产商分销商零售商运输时的成本（冷链或非冷链）均由上游企业承担。H2：各个企业都是理性的，都追求其自身的经济价值和信誉价值最大化。H3：农产品选择非冷链运输方式时，不会发生影响交货的重大变质，仅仅在影响其鲜活度。H4：假设模型中农产品为同质产品。H5：各层之间为非合作竞争的关系。H6：信誉价值只考虑于交易双方中的卖方，即在交易过程中买方处于较高地位。H7：相关成本函数和价值函数均为连续可微的凸函数。模型中的各个符号见表1。

1.3模型中各層企业双重价值目标分析

1.3.1农产品供应链超网络中各生产商的目标分析

生产商m在与分销商n的农产品冷链配送交易中，其经济收益为pmnqmn，经济成本包括3部分，农产品的生产成本cm（qm）；冷链带来的额外成本cmmn（lmn，qmn，rmn）（如冷链设施的购置成本、冷链配送中额外的油气费用等），此成本与冷链水平lmn、交易量qmn、运输距离rmn相关；与分销商n的交易成本cmbmn（qmn，hmn）（如搬运装卸费用、信息沟通费用、押金预付款等），此成本与交易量qmn、信誉度hmn有关。故其经济价值最大化即为：

[JZ][HT6，6"]maxU1=∑[DD（]Nn=1[DD）]pmnqmn-cm（qm）-∑[DD（]Nn=1[DD）]cmmn（lmn，qmn，rmn）-∑[DD（]Nn=1[DD）]cmbmn（qmn，hmn）；

[JZ（]s.t. qm=∑[DD（]Nn=1[DD）]qmn，qmn≥0，0≤lmn≤1，rmn≥0，hmn≥0，pmn≥0。[JZ）][JY]（1）

在交易过程中其获得的信誉价值与冷链水平、到货时间（假设冷链与非冷链配送速度相同，故此项可变为运输距离）、交易频率有关。故其信誉价值最大化即为：

[JZ（][JB（]maxU2=∑[DD（]Nn=1[DD）]hmn（lmn，rmn，fmn）；

s.t. 0≤lmn≤1，rmn≥0，fmn≥0。[JB）][JZ）][JY]（2）

生产商的多目标双价值最大化问题通常采取标准权函数来解决，本研究采用常数权重为1的标准权函数[15]，即企业认为在交易和配送过程中经济价值和信誉价同等重要。故生产商的双价值最大化决策为：

maxUm=U1+U2=∑[DD（]Nn=1[DD）]pmnqmn-cm（qm）-∑[DD（]Nn=1[DD）]cmmn（lmn，qmn，rmn）=∑[DD（]Nn=1[DD）]cmbmn（qmn，hmn）+∑[DD（]Nn=1[DD）]hmn（lmn，rmn，fmn）；

s.t. qm=∑[DD（]Nn=1[DD）]qmn，qmn≥0，0≤lmn≤1，rmn≥0，hmn≥0，pmn≥0，fmn≥0。[JY]（3）

根据假设H7，上式（3）为连续可微函数和变分不等式等价性，故公式（3）的解（q*mn，l*mn）等价于如下变分不等式的解：

∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmqmn[SX）]+[SX（]cmmnqmn[SX）]+[SX（]cmbmnqmn[SX）]-pmn[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmmnlmn[SX）]+[SX（]cmmnlmn[SX）]-[SX（]hmnlmn[SX）][JB））]（lmn-l*mn）≥0。[JY]（4）

1.3.2农产品供应链超网络中各分销商的目标分析

分销商n与零售商k交易过程中，其收益为pnkqnk，分销商n的成本包括从生产商m处购买农产品的成本pmnqmn，与生产商m的交易成本cnbmn（qmn，hmn），与零售商z交易配送时的冷链成本cnnk（lnk，qnk，rnk），与零售商z的交易成本cnbnk（qnk，hnk）。故cnbnk（qnk，hnk）其经济价值最大化即为：

maxV1=∑[DD（]Kk=1[DD）]pnkqnk-∑[DD（]Mm=1[DD）]pmnqmn-∑[DD（]Xm=1[DD）]cnbmn（qmn，hmn）-∑[DD（]Kk=1[DD）]cnnk（lnk，qnk，rnk）-∑[DD（]Kk=1[DD）]cnbnk（qnk，hnk）；

s.t. ∑[DD（]Mm=1[DD）]qmn≥∑[DD（]Kk=1[DD）]qnk，qmn≥0，qnk≥0，0≤lmn≤1，rnk≥0，hmn≥0，hnk≥0，pmn≥0，pnk≥0。[JY]（5）

在交易过程中其获得的信誉价值为hnk，信誉度与农产品的鲜活度、到货时间（假设冷链与非冷链配送速度相同，故此项可变为运输距离）、交易频率有关。故其信誉价值最大化即为：

[JZ（][JB（]maxV2=∑[DD（]Kk=1[DD）]hnk（lnk，rnk，fnk）；

s.t. 0≤lnk≤1，rnk≥0，fnk≥0。[JB）][JZ）][JY]（6）

分销商的多目标双价值最大化问题通常采取标准权函数来解决，采用常数权重为1的标准权函数[15]。故分销商的双价值最大化决策为：

maxVn=V1+V2=∑[DD（]Kk=1[DD）]pnkqnk-∑[DD（]Mm=1[DD）]pmnqmn-∑[DD（]Xm=1[DD）]cnbmn（qmn，hmn）-∑[DD（]Kk=1[DD）]cnnk（lnk，qnk，rnk）-∑[DD（]Kk=1[DD）]cnbnk（qnk，hnk）+∑[DD（]Kk=1[DD）]hnk（lnk，rnk，fnk）。[JY]（7）

根据假设H7，上式（7）为连续可微函數和变分不等式等价性，故公式（7）的解（q*mn，q*nk，l*mn，l*nk，β*）等价于如下变分不等式的解：

[JP4]∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（]pmn+[SX（]cnbmnqmn[SX）]-β[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]nn=1[DD）][JB（（][SX（]cnbmnlmn[SX）][JB））]（lmn-l*mn）+[JP3]∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（]β-pnk+[SX（]cnnkqnk[SX）]+[SX（]cnbnkqnk[SX）][JB））]（qnk-q*nk）+∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（][SX（]cnnklnk[SX）]+[SX（]cnbnklnk[SX）]-[SX（]hnklnk[SX）][JB））]（lnk-l*nk）+∑[DD（]Nn=1[DD）][JB（（]∑[DD（]Mm=1[DD）]qmn-∑[DD（]Kk=1[DD）]qnk[JB））]（β-β*）≥0。[JY]（8）

式中，β为拉格朗日乘子。

1.3.3农产品供应链超网络中各零售商的目标分析

零售商是否决定从分销商处购买农产品，取决于农产品的购买价格、其他成本和销售价格，即下式成立[16]：

[JZ（]pnk+ckdete（lmn，lnk，qnk）[JB（{]=p*k，qnk>0≥p*k，qnk=0[JB）]。[JZ）][JY]（9）

[JZ（]d*k=[JB（{]=∑[DD（]Nn=1[DD）]q*nk，p*k>0≤∑[DD（]Nn=1[DD）]q*nk，p*k=0[JB）]。[JZ）][JY]（10）

公式（9）说明零售商从分销商购买农产品的价格pnk，与单位变质成本ckdete（lmn，lnk，qnk）之和不能超过市场对产品的需求价格（即零售价格），此时零售商才会从分销商处购买产品出售给零售市场上的需求者（其中单位变质成本与农产品到达零售商时的鲜活度有关，即与农产品从生产商到分销商的冷链水平、从分销商到零售商的冷鏈水平和交易数量有关）。公式（10）说明在均衡状态下，如果零售市场中的消费者愿意购买此种农产品，则此时需求量恰好等于供给量，当供给大于需求时，市场中产品的价格为零。说明了农产品的零售市场为完全竞争市场，这与经济学中对农产品市场的说明一致。

由变分不等式互补形式的等价性，可将零售商的决策条件公式（9）、公式（10）转化为最优的（q*nk，p*k），即下式成立：

[HT6，6"][JZ（]∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）]（pnk+ckdete-pk）（qnk-q*nk）+∑[DD（]Kk=1[DD）][JB（（]∑[DD（]Nn=1[DD）]qnk-dk[JB））]（pk-p*k）≥0。[JZ）][JY]（11）

2农产品供应链双价值超网络模型均衡分析

由以上分析可知，农产品供应链的双价值超网络模型的均衡状态是存在唯一最优解（q*mn，l*mn，q*nk，l*nk，β*，p*k）满足公式（4）、公式（8）、公式（11）3式之和，即下式：

∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmqmn[SX）]+[SX（]cmmnqmn[SX）]+[SX（]cmbmnqmn[SX）]-pmn[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cmmnlmn[SX）]+[SX（]cmbmnlmn[SX）]-[SX（]hmnlmn[SX）][JB））]（lmn-l*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（]pmn+[SX（]cnbmnqmn[SX）]-β[JB））]（qmn-q*mn）+∑[DD（]Mm=1[DD）]∑[DD（]Nn=1[DD）][JB（（][SX（]cnbmnlmn[SX）][JB））]（lmn-l*mn）+∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（]β-pnk+[SX（]cnnkqnk[SX）]+[SX（]cnbnkqnk[SX）][JB））]（qnk-q*nk）+[JP4]∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）][JB（（][SX（]cnnklnk[SX）]+[SX（]cmbnklnk[SX）]-[SX（]hnklnk[SX）][JB））]（lnk-l*nk）+∑[DD（]Nn=1[DD）][JB（（]∑[DD（]Mm=1[DD）]qm-∑[DD（]Kk=1[DD）]qnk[JB））]（β-β*）+∑[DD（]Nn=1[DD）]∑[DD（]Kk=1[DD）]（pnk+ckdete-pk）（qnk-q*nk）+∑[DD（]Kk=1[DD）][JB（（]∑[DD（]Nn=1[DD）]qnk-dk[JB））]（pk-p*k）≥0。[JY]（12）

证明：

必要性：将公式（4）、公式（8）、公式（11）3式相加即得到式（12）。

充分性：将证明必要性时消掉的项加入到式（12），得到公式（4）、公式（8）、公式（11）加总后的公式，再将其分开为公式（4）、公式（8）、公式（11）式即可。

从公式（12）中可以得到农产品双价值超网络模型整体均衡的条件，即在3层交易模型中，各个企业在寻求各自经济价值和信誉价值最大化时，整体网络能在合理的冷链水平和交易量时达到均衡稳定状态，这时各个企业的双价值都达到了尽可能的最大化，而且交易网络也达到稳定的状态。

在对公式（12）进行求解变分不等式时，梯度投影算法可以求解连续凸函数的变分不等式的解，由于假设的函数都是凸函数且是利普希茨连续的，故使用一种改进后的投影梯度算法来求解[17]。

此算法经过确定初值、计算、改进、收敛保证4个步骤后得到变分不等式的解为：

qTmn=max[JB（[]0，qT-1mn-θ[JB（（][SX（]cmqmn[SX）]+[SX（]cmmnqmn[SX）]+[SX（]cmbmnqmn[SX）]+[SX（]cnbmnqmn[SX）]-βT-1n[JB））][JB）]]；

lTmn=min[JB（{]1，max[JB（[]0，lT-1mn-θ[JB（（][SX（]cmmnlmn[SX）]+[SX（]cmbmnlmn[SX）]-[SX（]hmnlmn[SX）]+[SX（]cnbmnlmn[SX）]）[JB））][JB）]][JB）}]；

qTnk=max[JB（[]0，qT-1nk-θ[JB（（]βT-1n+[SX（]cnnkqnk[SX）]+[SX（]cnbnkqnk[SX）]+ckdete-pT-1k[JB））][JB）]]；

lTnk=max[JB（[]0，lT-1nk-θ[JB（（][SX（]cnnklnk[SX）]+[SX（]cnbnklnk[SX）]-[SX（]hnklnk[SX）][JB））][JB）]]；

pTK=max[0，pT-1k-θ（∑[DD（]Nn=1[DD）]qT-1nk-dk）]；

βTn=max[0，βT-1n-θ（∑[DD（]Mm=1[DD）]qT-1mn-∑[DD（]Kk=1[DD）]qT-1nk）]。

其中T為迭代次数。

3数值仿真案例

本研究选择了上面的改进投影梯度算法来对超网络模型所得的变分不等式来进行优化求解。为便于分析，将模型简化，简化生产商、分销商和零售商个数都为2，即M=2、N=2、K=2。其余各个成本函数和交易函数为：

c1（q1）=2.1（q211+q212）-1 500（q11+q12），c2（q2）=2.1（q221+q222）-1 500（q21+q22）。

[JZ]hmn=2l2mn-0.1rmn+fmn，hnk=2l2nk-0.1rnk+fnk。

[JZ]cmbmn=0.3qmn-50hmn，cnbnk=0.3qnk-50hnk。

[JZ]cmmn=100lmn+0.1qmn，cnnk=100lnk+0.1qnk。

[JZ]dk=600-20pk。

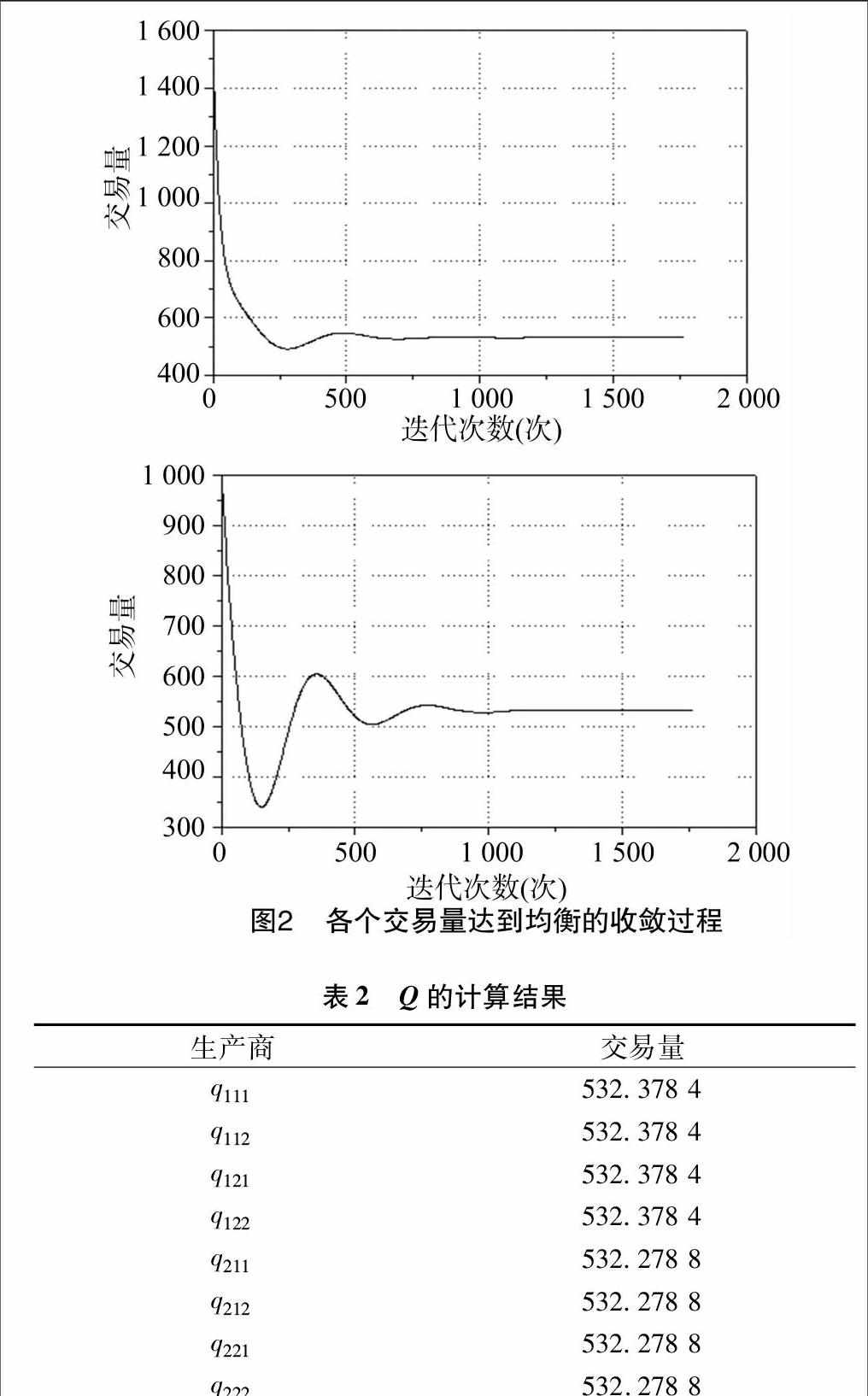
应用Matlab R2010b实现改进的投影梯度算法对模型进行求解，令收敛精度为0.001，将上面各函数求梯度带入变分不等式的解可得均衡解。花费3 s，迭代1 763步实现收敛，从图2可以看出，各个交易量随着迭代次数的增大而逐步收敛到一个不动点，即模型中各层企业交易量在收敛到不动点时，各方的竞合过程达到均衡，此时模型得到了均衡解。故此模型的均衡解为：lmn=lnk=1，p1=p2=3。在设计价值函数时，假设企业对其经济价值和信誉同等看重，则其冷链水平均为1，即在企业认为经济价值和信誉价值同等重要时，最优冷链水平为1。企业会尽可能提高自己的冷链配送水平，以达到经济价值和信誉价值最大化。各企业间的均衡交易量见图2（横轴为迭代次数，纵轴为交易量）。

从图2可以看出，超网络各层交易量不断振荡直到达到均衡的过程，表明了交易量在本仿真试验中可以逐渐收敛并达到最终稳定，证明了仿真试验中各式的正确性和数据的合理性。

从表2可以看出，q111、q112、q121、q122分别代表2个生产商M=1，2与2个分销商N=1，2的交易量，q211、q212、q221、q222分别代表2个分销商N=1，2与2个零售商K=1，2的交易量。

供应链同层企业存在竞合关系，各层企业的交易流量应该是基本相同的，从分析结果可以看出，生产商与分销商的交易量和分销商和零售商的交易量大致相同，证明了模型的正确和有效。各层企业的双价值函数都包括经济价值和信誉价

[值，且假设各个企业2个价值函数权重都相同，在这种情况下，冷链水平为1时，此模型达到均衡，证明在企业认为经济价值和信誉价值同等重要的情况下，冷链水平达到1时，双价值能达到最大。对于新兴的冷链配送企业，当其认为信誉价值比经济价值重要时，均衡的冷链水平和交易量即会发生变化。因此对于不同的企业，当其有不同的双价值权重时，相应的均衡交易量和冷链水平也会随之变化。

4结论

本研究构建了农产品供应链超网络双价值模型，探讨了农产品冷链运输物流网络中各个企业在追求双价值最大化时，整个供应链模型的动态均衡条件，并对模型进行了仿真试验和数值分析。即构建了3层冷链网络均衡模型，利用变分不等式求得各层企业各自双价值最大化时的决策，并最终得到整个网络模型均衡条件，随后利用改进后的投影梯度算法对仿真模型进行求解分析。结果表明，合理的冷链水平和交易量能使整个农产品冷链物流配送网络达到均衡状态，给农产品冷链物流配送网络中的各个企业和整体网络的长期均衡发展提供了科学的分析方法和指导意义。

今后研究中，需要继续优化模型使其与实际冷链配送情况更加一致，进一步放开假设条件和完善限制条件，并结合现实冷链配送情景，求出更符合现实的均衡条件，提供更好的决策建议。

参考文献：

[1]冷志杰，唐焕文. 大宗农产品供应链思维网络模型及应用[J]. 系统工程理论与实践，2005，3（3）：39-45.

[2]赵霞，窦建平. 求解农产品供应链网络设计问题的混合粒子群算法[J]. 管理工程学报，2013，27（4）：169-177.

[3]但斌，陈军. 基于价值损耗的生鲜农产品供应链协调[J]. 中国管理科学，2008，16（5）：42-49.

[4]廖莉. 农产品供应链网络模型及优化策略研究[D]. 济南：山东大学，2011.

[5]黄纯辉. 食品冷链物流运输服务网络优化研究[D]. 武汉：武汉理工大学，2012.

[6]Nagurney A，Dong J，Zhang D. A supply chain network equilibrium model[J]. Transportation Research Part E Logistics & Transportation Review，2002，38（5）：281-303.

[7]Low S H，Paganini F，Doyle J C.Internet congestion control[J]. IEEE Control Systems Magazine，2002，22（1）：28-43.

[8]席运江，党延忠，廖开际. 组织知识系统的知识超网络模型及应用[J]. 管理科学学报，2009，12（3）：12-20.

[9]Bautu E，Kim S，Bautu A，et al. Evolving hypernetwork models of binary time series for forecasting price movements on stock markets[C]. IEEE Congress on Evolutionary Computation，2009：166-173.

[10]Matsypural D，Nagurney A，Liu Z. Modeling of electric power supply network with fuel suppliers viavariational inequalities[J]. International Journal of Emerging Electric Power Systems，2007，8（1）：1-5.

[11]Sonntag M，Teichert H M. Competition hypergraphs[J]. Discrete Applied Mathematics，2004，143（1/2/3）：324-329.

[12]Emmerink R H M，Axhausen K W，Nijkamp P，et al. Effects of information in road transport networks with recurrent congestion[J]. Transportation，1995，22（1）：21-53.

[13]王眾托，王志平. 超网络初探[J]. 管理学报，2008，5（1）：1-8.

[14]漆玉虎，郭进利. 超网络研究[J]. 上海理工大学学报，2013，35（3）：227-239.

[15]Nagurney A，Ke K. Financial networks with electronic transactions：modelling，analysis and computations[J]. Quantitative Finance，2003，3（2）：71-87.

[16]Bertsekas D P，Tsitsiklis J N. Parallel and distributed computing[M]. New Jersey：Prentice-Hall，1989.

[17]Korpelevich G M. The extragradient method for finding saddle points and other problems[J]. Matecon，1976，12：747-756.