基于BP-EKF算法的锂电池SOC联合估计*

孔祥创，赵万忠，2，王春燕，2

(1.南京航空航天大学能源与动力学院，南京210016;2.重庆大学，机械传动国家重点实验室，重庆400044)

基于BP-EKF算法的锂电池SOC联合估计*

孔祥创1，赵万忠1，2，王春燕1，2

(1.南京航空航天大学能源与动力学院，南京210016;2.重庆大学，机械传动国家重点实验室，重庆400044)

电池荷电状态(SOC)的准确估计是电动车辆进行整车控制优化的先决条件，也是合理实施电池管理的依据。本文中在确定1阶RC等效电路模型的基础上，采用含有遗忘因子的递推最小二乘算法和BP-EKF算法对模型参数与SOC进行在线联合估计，提出一种BP神经网络和扩展卡尔曼滤波(EKF)相结合的锂离子动力电池SOC估计方法，使用相应的滤波输出参数离线训练BP神经网络，进而将训练成功的BP神经网络用于补偿EKF算法的估计误差。通过仿真和电池动态工况试验验证，结果表明，与EKF算法相比，所提出的SOC估计方法具有良好的抑制发散和鲁棒性能，能有效提高SOC的估计精度。

锂电池;荷电状态;扩展卡尔曼滤波;BP神经网络;联合估计

前言

电动汽车SOC是描述电池使用过程中剩余电量的重要参数［1］。然而，电池的SOC无法采用传感器直接测得，它必须通过对一些其他物理量的测量并采用一定的数学模型和算法来估计得到［2］。同时，动力电池在使用过程中由于受到许多内外不确定因素的影响，常常表现出高度的非线性，又增加了准确估计SOC的难度［3］。

现有对动力电池SOC估计方法的研究主要包括放电实验法、安时积分法、开路电压法和卡尔曼滤波法等方法。放电实验法适用于所有电池，在实验室中经常使用，但不适合行驶中的电动汽车，不能在线对SOC进行测量［4］。安时积分法随着时间延长会产生累计误差，开路电压法无法实现实时估计［5］。文献［6］中建立开路电压法、安时积分法和卡尔曼滤波法的组合方法估计电池SOC，提高了SOC估计的精度。其不足在于模型参数通过离线辨识得到，导致模型精度不高，而扩展卡尔曼滤波对模型精度要求高，容易受到噪声的影响导致滤波发散，进而影响SOC估计的精度。因此，如何利用电池可测参数来实现当前电池剩余电量准确估算一直以来是电池管理系统的核心问题和急需解决的技术难点。

本文中选用1阶RC等效电路模型，将含有遗忘因子的递推最小二乘法进行模型参数辨识与SOC估计联合的同时，利用BP神经网络和扩展卡尔曼滤波相结合的SOC估计算法，克服了扩展卡尔曼滤波算法对电池模型精度依赖性强、滤波容易发散的问题，提高了算法的估计精度和鲁棒性。

1 电池建模

电池模型对于SOC估计算法具有重要意义，其精度直接影响SOC估计的准确性。考虑到受电池管理系统计算和存储能力的限制，动力电池模型必需满足结构简单、计算速度快和预测精度高等特点。本文中选用1阶RC等效电路模型，见图1。

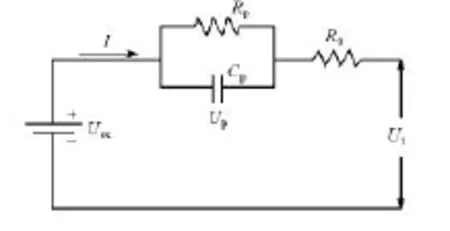
图11 阶RC等效电路模型

图中Uoc为开路电压，Ut为端电压，I为电池工作电流，Rp为极化电阻，Cp为极化电容，Up为Rp上的极化电压降，R0为电池的欧姆内阻。

由基尔霍夫定律得

开路电压Uoc与SOC为一一对应关系，对估计电池SOC起重要作用，以额定容量为2.3A·h的单体锂电池为试验对象，利用低电流充放电方法获得OCV-SOC曲线(图2)，为下文研究模型参数辨识和SOC估计提供基础。其具体步骤如下:(1)给电池充满电，放置12h;(2)以1/10C恒流放电直到其放电截止电压;(3)放置12h;(4)以1/10C恒流充电直到其充电截止电压;(5)取充电和放电电压的平均值。

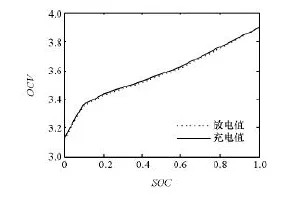
图2OCV-SOC曲线

2 模型参数辨识

由于普通的最小二乘法不能实现模型参数的实时在线辨识，因此本文中采用含有遗忘因子的递推最小二乘法［7］，可有效实现模型参数的实时更新，对提高SOC估计精度有很大作用。

含有遗忘因子的递推最小二乘法辨识步骤［8］:

式中:K(k)为递推最小二乘增益矩阵;P(k)为协方差矩阵;h(k)为观测矩阵;λ为遗忘因子，通常λ=［0.95，1］;I为单位矩阵;θ^(k)为参数估计矩阵; y(k)为k时刻的观测值;e(k)为输出估计误差矩阵。

需要辨识的模型参数有R0，Rp，Cp，设置系统输入为测量电流值，输出为电池端电压。对式(2)求导得

由于采样时间内电阻R0变化很小，即R·0≈0。将式(1)和式(2)代入式(4)得

定义Et=Ut－Uoc，T为采样时间，将式(5)离散化得

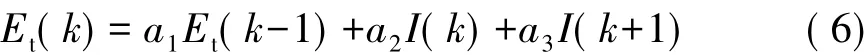
其中a1，a2，a3和待辨识模型参数的关系为

式中Et(k－1)=Ut(k－1)－Uoc(k－1)。Ut(k)，Ut(k－1)，I(k)和I(k－1)均由电压传感器和电流传感器测量得到，Uoc(k－1)为k－1时刻的电池开路电压，开路电压不能在线测得，这里根据OCV-SOC曲线和BPEKF算法实时估计的SOC反馈值算得。运行含遗忘因子的递推最小二乘法，辨识出参数a1，a2和a3后，即可由式(7)估计出电池模型参数。

3 SOC估计方法

3.1 扩展卡尔曼滤波(EKF)

对如图1所示的1阶RC电池模型，结合安时积分法，以SOC和电容Cp两端的电压Up为状态变量，充放电电流I为输入量，电池端电压Ut为输出量，可得到离散化的状态空间模型:

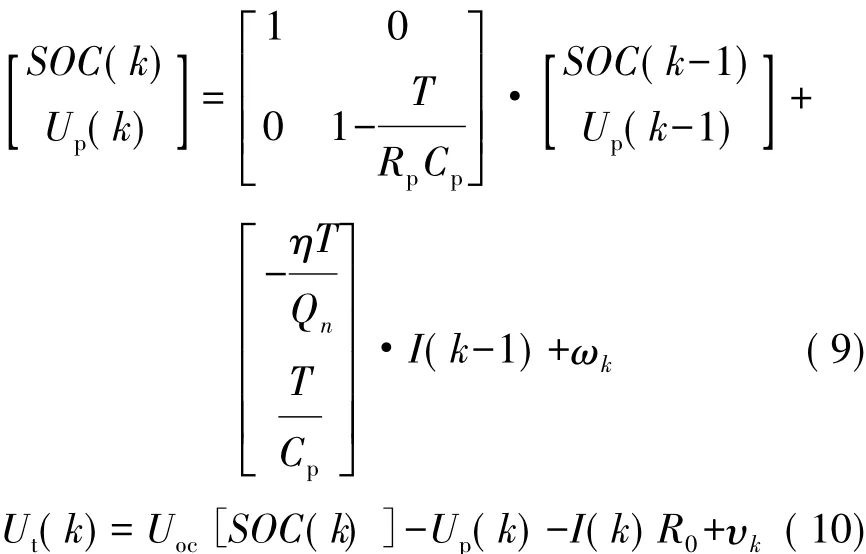
式中:η为库伦效率，可通过电池充放电试验得到;T为采样周期;Qn为电池额定容量;ωk为不可测量的随机输入量;υk为电池端电压的测量噪声。

在此模型的基础上，采用扩展卡尔曼滤波算法估计电池的SOC。

扩展卡尔曼滤波循环迭代过程为［9］

式中:P为均方估计误差;Ak－1为k－1时刻的状态方程矩阵;H=Ut/SOC为观测矩阵;e为端电压观测输出误差;Utk为k时刻的端电压观测值;x为状态变量;Q和R为观测噪声和系统噪声。

3.2 利用BP神经网络改进EKF算法

由于BP神经网络具有较强的学习能力和复杂映射能力，所以可对其进行离线训练并用于在线补偿EKF算法，以提高滤波精度，避免滤波发散［10］。

利用BP神经网络对EKF算法改进的步骤:

步骤一、BP神经网络训练。利用Matlab神经网络工具箱建立一个三输入一输出的3层BP神经网络，隐含层神经元为14个，最大迭代次数5 000次，期望值为1×10－5。采集电池充放电时的电压、电流数据，利用EKF算法进行2 000次滤波，并将端电压观测输出误差e、卡尔曼滤波增益K、状态预测值与最优估计值之差xk+1－x^k+1|k，作为神经网络的输入，SOC真实值与滤波后最优估计值之差SOC－SOC^作为神经网络的输出。以上就是神经网络的主要数据库。从数据库中随机提取样本总数的80%为训练样本，20%的样本作为测试样本，用于检验测试精度。对所设计的神经网络进行训练，使网络误差逐渐贴近期望值，当达到预期的期望值时，证明所需BP神经网络训练完成。

步骤二、模型参数和EKF算法的联合估计。图3为SOC估计总流程图。从图中可以看出，基于实时的电池测量数据，使用带有遗忘因子的递推最小二乘法(FFRLS)实现电池模型参数的一步辨识;然后使用EKF在获得更新的模型参数基础上完成SOC的估计，同时根据此时的SOC值，由OCV-SOC曲线得出更新的开路电压值，代入到FFRLS算法中，完成模型参数的二步辨识，以此类推实现模型参数和EKF算法的联合估计。

步骤三、BP网络和EKF联合估计。如图3所示，BP神经网络训练成功后，即可利用其辅助EKF进行在线状态估计。当接收到端电压观测量Utk后，滤波器EKF将提供e，K，xk+1－x^k+1|k。然后，将它们输入到训练成功的BP神经网络中，经神经网络算得SOCBP=SOC－SOC^。最后，得到EKF滤波后的最优估计和神经网络的输出之和SOCf=SOCEKF+SOCBP即为基于BP神经网络联合EKF的最优估计值。

小伙子家很穷。姑娘的父母当时特别反对这门婚事，但姑娘看上了小伙子的人，执意要嫁，便在家人的反对中，毅然嫁给了小伙子。

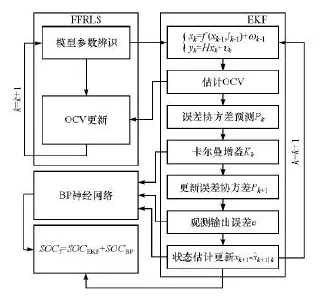
图3SOC估计总流程图

4 试验结果

为验证模型参数辨识的可靠性和本文中提出的SOC估计算法的准确性，使用电池动态工况试验数据(图4)进行验证，电池动态工况试验可反映试验情况下电池动态状态。初始SOC值为0.9，试验温度设置为恒温25℃，放电电流为正，充电电流为负。

图4 动态工况采样电流值

使用FFRLS在线辨识模型参数时，设置算法协方差的初始值P0=105×E，其中E为单位矩阵，E= diag(1，1，1)。设置好初始值后，使用matlab/simulink仿真软件，可得到在线的模型参数结果。将模型参数辨识值代入到建立的电池模型中估计出电池的端电压，并与动态工况采集的端电压作对比，进行误差分析，既可验证联合在线参数辨识的精确性，也可评估模型的合理性。图5为端电压估计值与试验测试值曲线对比。从图中可以看出，所设计的在线辨识方法能够较好地实现对动力电池的动态端电压变化的精确模拟。端电压估计误差如图6所示，误差结果普遍在0.03V以内，最大相对误差也低于3%，说明联合在线参数辨识方法能获得精准的模型参数，进而提高SOC估计精度。

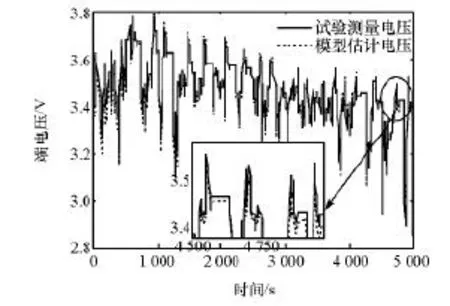
图5 端电压估计值与试验测试值曲线

图6 端电压估计值与试验测试值误差

在上述分析的基础上，将进一步验证SOC估计的准确性。图7为SOC估计值与试验值的对比。从图中可以看出，BP-EKF算法SOC仿真值基本在测量值附近细微波动，具有良好的收敛性。而EKF算法的SOC值却有很大波动，其稳定性不如BPEKF算法。

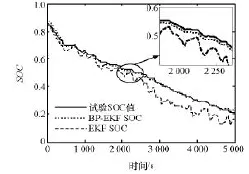
图7SOC估计值与试验值的比较

图8 为SOC估计误差，表1为具体的SOC估计误差分析。从图8和表1中可以看出，BP-EKF算法最大误差为2.78%，均值误差和均方根误差分别为0.22%和0.83%。而EKF算法的最大误差为10.76%，均值误差和均方根误差分别为5.82%和3.43%。因此，基于BP-EKF算法的SOC估计，优于EKF算法，并可通过BP神经网络的修正与补偿，得到更为精确的估计值。

图8SOC估计误差

表1 SOC估计误差分析%

5 结论

(1)在1阶RC等效电路模型的基础上使用基于遗忘因子的递推最小二乘法实现模型参数和SOC估计的联合在线辨识，这对提高模型参数估计精度有很大作用。

(2)提出了BP-EKF估计算法。利用BP神经网络辨识的补偿误差值优化EKF算法，提高了EKF算法的估计精度和可靠性。

(3)基于仿真和试验测试完成了估计算法的验证。结果表明:BP-EKF算法可以达到较为精确的估计结果，估计误差小于2%。

［1］华周发，李静．电动汽车动力电池SOC估算方法综述［J］．电源技术，2013，37(9):1686－1689．

［2］XIONG Rui，SUN Fengchun，et al．A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles［J］．Applied Energy，2013，63(6):1421－1433．

［3］PLETT G．Extended kalman filtering for battery management systems of LiPB-based HEV battery packs，Part 1，Background［J］．J．Power Sour，2004，134(2):252－261．

［4］黄文华，韩晓东，陈全世，等．电动汽车SOC估计算法与电池管理系统的研究［J］．汽车工程，2007，29(3):198－202．

［5］杨世春，麻翠娟．基于PNGV改进模型的SOC估计算法［J］．汽车工程，2015，37(5):582－586．

［6］林成涛，陈全世，王军平，等．用改进的安时计量法估计电动汽车动力电池SOC［J］．清华大学学报(自然科学版)，2006，46 (2):247－251．

［7］XIONG Rui，HE Hongwen，ZHAO Kai．Research on an online identification algorithm for a thevenin battery model by an experimental approach［J］．International Journal of Green Energy，2015，12(3):272－278．

［8］HU Xiaosong，SUN Fengchun，et al．Online estimation of an electric vehicle Lithium-Ion battery using recursive least squares with forgetting［C］．Proceedings of 2011 American Control Conference，San Francisco，California，2011:935－940．

［9］张利，朱雅俊，刘征宇．锂离子电池SOC与模型参数联合估算研究［J］．电子测量与仪器学报，2012，26(4):320－324．

［10］VILA J P，WAGNER V，NEVEU P．Bayesian nonlinear model selection and neural network:A conjugate prior approach［J］．IEEE Trans on Neural Networks，2000，11(2):265－278．

Co-estimation of Lithium Battery SOC Based on BP-EKF Algorithm

Kong Xiangchuang1，Zhao Wanzhong1，2＆Wang Chunyan1，2
1.College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing210016; 2.Chongqing University，State Key Laboratory of Mechanical Transmission，Chongqing400044

Accurate estimation of battery SOC is not only a prerequisite for control and optimization of electric vehicle，but also the basis for the reasonable implementation of battery management．In this paper，based on the first-order RC equivalent circuit model，a SOC estimation method for lithium power battery is proposed by combining BP neural network with extended Kalman filtering(EKF)，in which recursive least-squares with forgetting factor and BP-EKF algorithm are adopted to conduct a co-estimation of SOC and other model parameters．Corresponding filter output parameters are used to train BP neural network off-line，and succed trained BP neural network are used to compensate the estimation error in EKF algorithm．The results of simulation and dynamic state test show that compared with EKF algorithm，the SOC estimation method proposed has good performances in divergence suppression and robustness，and can effectively enhance the estimation accuracy of battery SOC．

lithium battery;SOC;extended Kalman filtering;BP neural network;co-estimation

10．19562/j．chinasae．qcgc．2017．06．007

*国家自然科学基金(51375007)、重庆大学机械传动国家重点实验室开放基金(SKLMT-KFKT-2014010和SKLMT-KFKT-201507)和江苏省普通高校研究生科研创新计划项目(SJZZ15_0038)资助。

原稿收到日期为2016年6月7日，修改稿收到日期为2016年8月15日。

赵万忠，教授，E-mail:zhaowanzhong@126．com。