基于工艺特征约束的改进遗传算法①
张 节, 沈建新, 田 威
(南京航空航天大学 机电学院, 南京 210016)
基于工艺特征约束的改进遗传算法①
张 节, 沈建新, 田 威
(南京航空航天大学 机电学院, 南京 210016)
为提高飞机装配的精度, 减小定位的误差, 优化具有复杂工艺特征的机身框件的支撑序列. 针对优化中工艺特征约束处理问题, 建立了工艺特征约束的广义数学模型, 从理论角度提出了一种针对此类约束的不可行解修补算法, 并基于此算法设计一种改进的遗传算法. 使用改进的遗传算法优化某型飞机机身框在可重构柔性工装上的支撑序列, 优化过程稳定, 最优序列下框的柔性定位误差减小93.08%, 保证了飞机装配的精度. 理论基础分析和仿真结果分析表明, 改进的遗传算法通用性强, 适用于各种约束优化问题; 收敛速度快且稳定, 具备可行性.
装配精度; 遗传算法; 约束优化; 修补算法; 工艺约束; 飞机装配
随着现代飞机制造技术的发展, 飞机产品的快速更新换代, 飞机装配已逐渐向自动化、数字化发展, 可重构柔性装配工装以其可变性与通用性的特点广泛应用于国外数字化装配领域, 国内也开始重点发展这一项智能装备技术. 装配过程伴随着误差的产生, 如果误差累积过大, 会导致飞机的关键装配特性超出其目标值, 对装配质量和周期造成严重的影响[1]. 因此, 对装配件的定位误差控制已成为急需解决的问题. 定位误差的来源分为刚性和柔性两部分[2]. 其中刚性部分主要来源于工装的制造和安装, 郭飞燕等[3]建立了误差模型,并用补偿法抑制了该种误差; 柔性部分主要来源于装配件的形变, 这也是本文研究的目的, 即通过优化定位/支撑的点阵布局来抑制柔性定位误差.
考虑到飞机框件的复杂工艺特征, 框件在可重构柔性工装上的支撑序列优化可以作为一种具有工艺特征约束的约束优化问题来处理. 其中, 工艺特征约束是约束条件在实际中的体现, 从狭义角度, 以机身框件为例, 主要包括交错布置的加强筋和不规则的边缘形状等工艺特征; 从广义角度, 主要包括等式、不等式约束和设计变量定义区间约束(如设计变量定义区间不连续且设计域离散). 求解约束优化问题的算法包括确定性算法和智能型算法[4]. 确定性算法(如投影梯度法、牛顿法、拉格朗日法等)要求目标函数在定义域内连续可微, 因此具有离散设计域约束优化问题无法解决.而智能优化算法在设计相对应的约束处理技术后, 均可用于求解约束优化问题. 鉴于智能优化算法是一类基于无约束的优化搜索技术, 在工程中使用智能算法处理约束优化问题时, 需要设计一种相对应的约束处理技术[5]. 约束处理技术作为当今研究热点, 常见的包括惩罚函数法、转化法、解码法等[6]. 惩罚函数法是最常用的方法, 通过在适应值函数上加惩罚项, 从而将约束问题变为无约束问题. BARBOSA等[7]提出一种基于违反约束程度的自适应惩罚函数法处理约束优化问题;与其相似的还有HO PY[8]和DEB K[9], DEB K将自适应策略用于增广拉格朗日乘子法, 提出改进的约束优化遗传算法, 试验证明该法具有高效性和精确性; 此外,还有MONTEMURRO[10]提出的自动动态惩罚函数法.转化法是另一热门技术, 该法直接将违反约束条件程度转化为优化目标, 从而将约束优化转化为无约束多目标优化问题, 如王俊年等[11]从多目标优化方法的角度出发, 将约束违背程度作为新的优化目标完成约束优化; TAKAHAMA T和SAKAI S[12]提出α约束法, 该法采用约束满足水平表示个体满足约束条件的程度. 转化法或将个体区分为可行解和不可行解分别处理, 如林丹[13]提出调整违反约束条件程度阈值的方式, 自适应确定不可行解比例. 其它约束处理技术也是当今研究热点, 如王晓圆等[14]针对遗传算法中染色体, 提出染色体的约束检查和调整技术, 解决了复杂约束问题; 甘敏[15]等将多目标优化法和自适应惩罚函数法结合, 提出稳健的新方法; Zhang C等[16]改进元启发式算法, 提高其搜索性能的同时引入可行性与支配性规则, 并验证了算法在处理约束优化问题时的精度和效率.
然而, 这些已有处理技术对不可行解通常采用“保留并改善”的对策, 依靠优化操作过程本身来处理. 在框件支撑序列优化中工艺特征约束下, 算法随机性将在运行过程中产生大量不可行解, 从而影响找到可行解的概率; 且由于需要将优化程序与ANSYS等其他大型软件联合使用, 这些已有技术产生的不可行解常造成算法效率低、稳定性差甚至不可行等问题. 因此, 设计一个计算复杂度低、能处理工艺特征约束条件的约束处理算法, 具有一定的工程意义. 考虑到相比于其它算法, 遗传算法不涉及搜索的方向、步长等参数, 且不失一般性, 本文面向交点孔定位的框件, 优化其支撑序列来减小装配中的定位误差. 针对支撑序列优化中的工艺特征约束, 提出一种不可行解修补算法, 并依此改进遗传算法, 完成优化, 最后验证该算法的可行性.
1 修补算法的原理
1.1 工艺特征约束的广义数学模型和分析
不失一般性, 设优化问题有n个独立的设计变量xi(i=1, 2,…, n), 则工艺特征约束(如图1)的广义数学模型如式(1)所示. 即变量在上下界中有m个不连续的定义区间; 有k个独立变量满足等式约束, l个独立变量满足不等式约束.
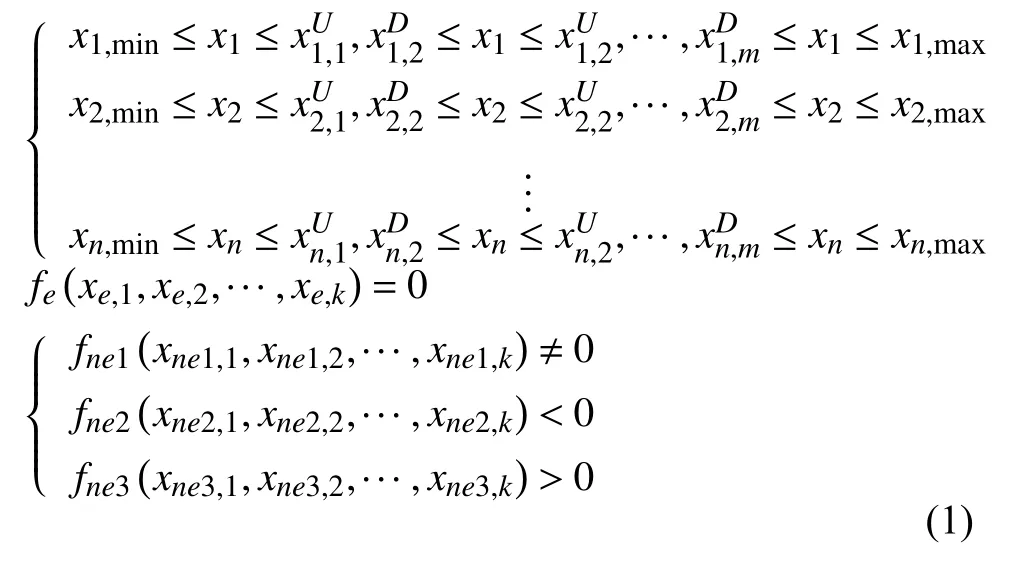
其中xn,min、xn,max为设计变量极值,为区间边界.
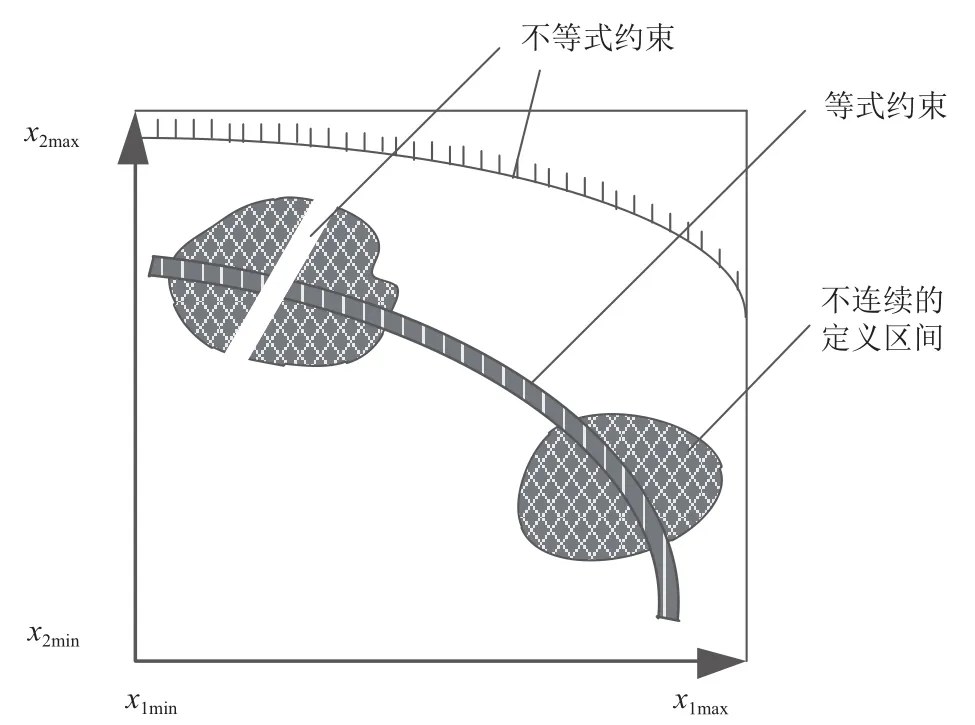
图1 2个设计变量时的2维离散设计域
因此, 约束优化迭代过程中, 设计变量的解将产生以下四种问题:
(1) 设计变量不满足定义区间约束;
(2) 设计变量不满足等式约束;
(3) 设计变量不满足不等式约束;
(4) 设计变量无解(没有满足约束的解).
对于第四种问题, 其产生的原因在于约束过多, 解决方法为重新建立优化数学模型, 本文不再赘述. 对于前三种问题, 本文提出一种有效的修补算法思路: 先处理违反等式约束的问题, 再处理违反不等式约束的问题, 最后处理定义区间约束的问题.
1.2 算法流程
针对任一设计变量xi进行讨论, 设其在上下界区间内具有不连续的定义区间(如图2).
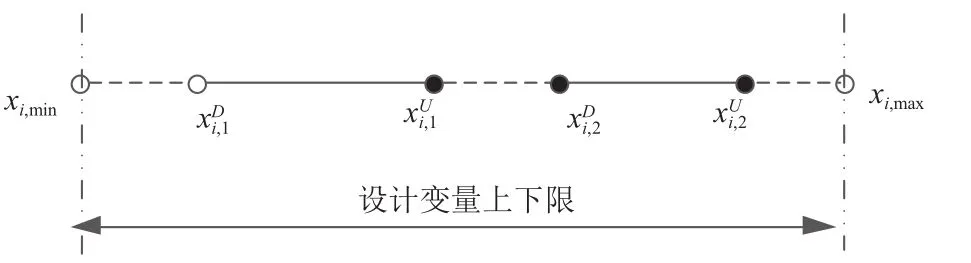
图2 设计变量不连续定义区间
Step1. 检查xi是否处于中. 若否, 则在内随机生成新值(如图3(a));
Step2. 检查xi是否满足等式约束. 若否, 根据等式
fe=0获取xi与其他设计变量的关系, 在内调整xi, 并相应调整其他设计变量, 使等式约束条件成立(如图3(b));
Step3. 检查xi是否满足不等式约束. 若否, 根据不等式获取xi与其他设计变量的关系, 在中满足等式约束的区间内调整xi, 并相应调整其他设计变量, 使等式约束条件成立的同时不等式约束条件也成立(如图3(c));
Step4. 检查xi是否落入不连续的定义区间. 若否,则在满足等式与不等式约束的区间内调整xi至定义区间,同时根据上述变量关系相应调整其它未落入区间的设计变量, 直至所有设计变量落入定义区间(如图3(d)).
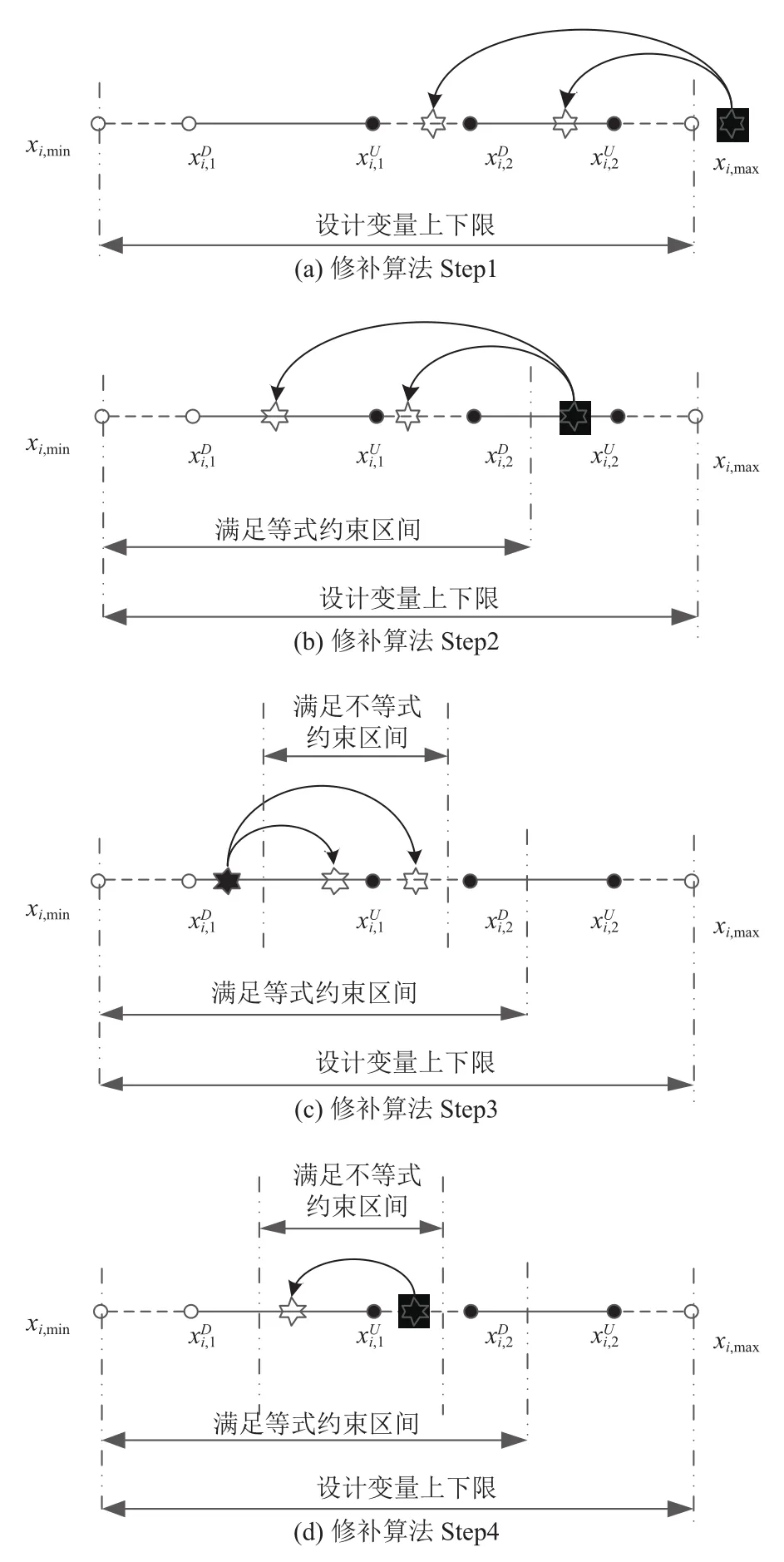
图3 修补算法图解
1.3 算法复杂度分析
由上述流程可得, 算法伪代码如下:
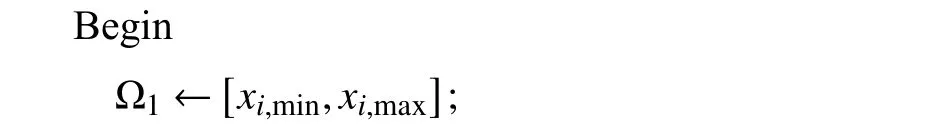


不失一般性, 假设设计变量的个数为n, 且所有设计变量均在变量上下界之外, 则该算法的复杂度如式(2):
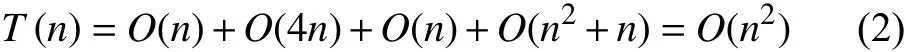
由复杂度可知, 该算法计算复杂度低, 且设计变量越少越简单. 因此, 进行基于该算法的优化之前, 可以使用灵敏度分析简化设计参数, 以增大优化效率.
2 改进遗传算法及工程应用
2.1 背景介绍
飞机装配是指将大量的飞机零件、标准件等按设计要求和技术条件在工艺装备上进行结构铆接、系统安装等全过程[17]. 为保证飞机装配的精度, 需要采用大量的装配工装[18]. 可重构柔性工装作为装配工装的前沿产品, 实现数字量在飞机制造过程中的全流通, 其关键技术的突破将为相关行业的发展带来巨大的机遇[19].可重构柔性工装关键技术中, 装配件支撑/定位方案的设计与优化成为解决定位误差的方法之一, 同时也是近几年的研究热门. 张洪双等[20]设计了一种三坐标数控定位器, 并使用遗传算法优化了定位器的布局和最优行程; 金栋平等[21]针对机翼后缘的柔性支撑结构, 完成了其布局优化设计; 盖玉春等[22]对飞机调姿工装的支撑位置进行了优化; XIONG L等[23]和LU C等[24]分析了“N-2-1”定位原则, 并使用遗传算法优化了薄壁件的支撑序列, 以减小加工过程中的形变定位误差.
本文笔者所在课题组针对某型飞机机身的立式装配设计了一种可重构柔性工装. 基于框件的交点孔定位方式, 该工装由4根筒状定位器进行“销-孔”定位与支撑. 由于框件在装配中因柔性形变而引起定位误差, 考虑到装配精度要求(0.05 mm)的要求, 定位器的布置序列需要优化.
2.2 优化数学模型
采用遗传算法对框的支撑序列进行优化, 将4根支撑件中心的极坐标作为设计变量, 中心点坐标处于可行域内(如图4)作为约束条件, 框的最大形变定位误差作为目标函数, 其数学模型如式(3):
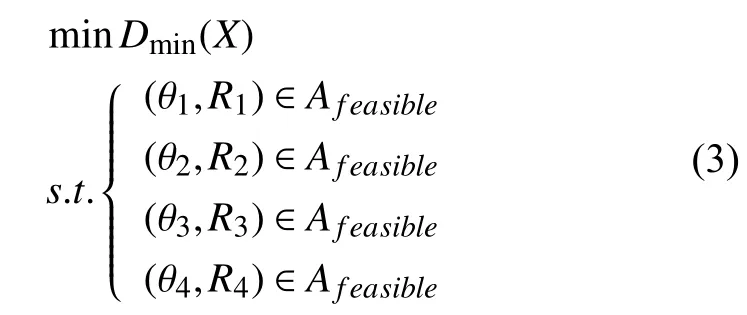

图4 支撑中心点在工艺特征约束下的可行设计域
2.3 面向飞机装配的工艺特征约束分析
在该框件的支撑序列优化中, 工艺特征约束在广义上涉及不连续的定义区间和不等式约束. 例如, 当θ=1.5π时, 其约束类型在极坐标下如图5所示.
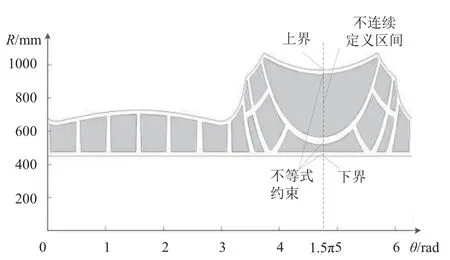
图5 某型飞机机身框的工艺特征约束
其不连续定义区间的约束在狭义层面上体现于加强筋和边缘的约束. 为了孔的位置不在加强筋上, 且定位器与加强筋不发生干涉, 需要使支撑件与加强筋和边缘保持一定距离. 同时, 加强筋布置的复杂性和边缘曲线的不规则性, 导致设计域被分隔为很多不规则的块, 即离散的设计域.
其不等式约束在狭义层面上体现于极坐标下两个坐标参数之间的关系. 因为框的边缘为不规则的曲线,极坐标下框上各点的半径与角度成函数关系, 因此合理的半径应该处于各角度对应的最大值与最小值之间.
2.4 改进的遗传算法
考虑到框件中工艺特征约束, 需要对优化算法进行约束处理. 然而常规的惩罚函数法等处理技术在该类工程问题中复杂、低效、稳定性差, 且优化过程中不可行解无法在导入ANSYS等有限元软件后完成仿真分析, 严重制约优化的可行性. 因此, 基于上述修补算法改进遗传算法.
改进后的遗传算法流程如下:
Step1. 设定参数, 生成满足工艺约束条件的初始种群, 种群中个体为所有支撑点的坐标信息;
Step2. 使用ANSYS软件进行有限元仿真分析, 计算所有个体对应的工件最大形变量;
Step3. 进入遗传操作循环;
Step4. 适应度值计算, 选出种群中的精英解;
Step5. 对种群执行选择操作;
Step6. 对种群执行交叉操作;
Step7. 对种群执行变异操作;
Step8. 使用修补算法修正种群;
Step9. 使用ANSYS软件仿真分析新种群个体对应的工件最大形变量, 使用精英解淘汰并替换产生形变量较大的个体, 得到新一代种群;
Step10. 判断是否达到停止标准, 即判断是否达到最大迭代次数, 或工件上最大形变量小于形变许用值且稳定于该最优值. 若已到, 则输出最优解, 程序停止.若未到, 则转到Step3.
该改进的遗传算法流程图如图6所示.
3 优化结果及讨论
(1) 通过运行改进的遗传算法, 迭代得到用于支撑/定位用的交点孔的最佳序列, 即框的最佳支撑序列如图7所示. 图中各交点孔的位置在框内且保证了定位器不与框产生干涉. 框件在最佳支撑序列下最大误差为0.02091 mm, 满足装配要求(0.05 mm), 且相比于原始设计方案(0.3022 mm)减小93.08%. 综上可以看出该改进的算法具有可行、有效性.
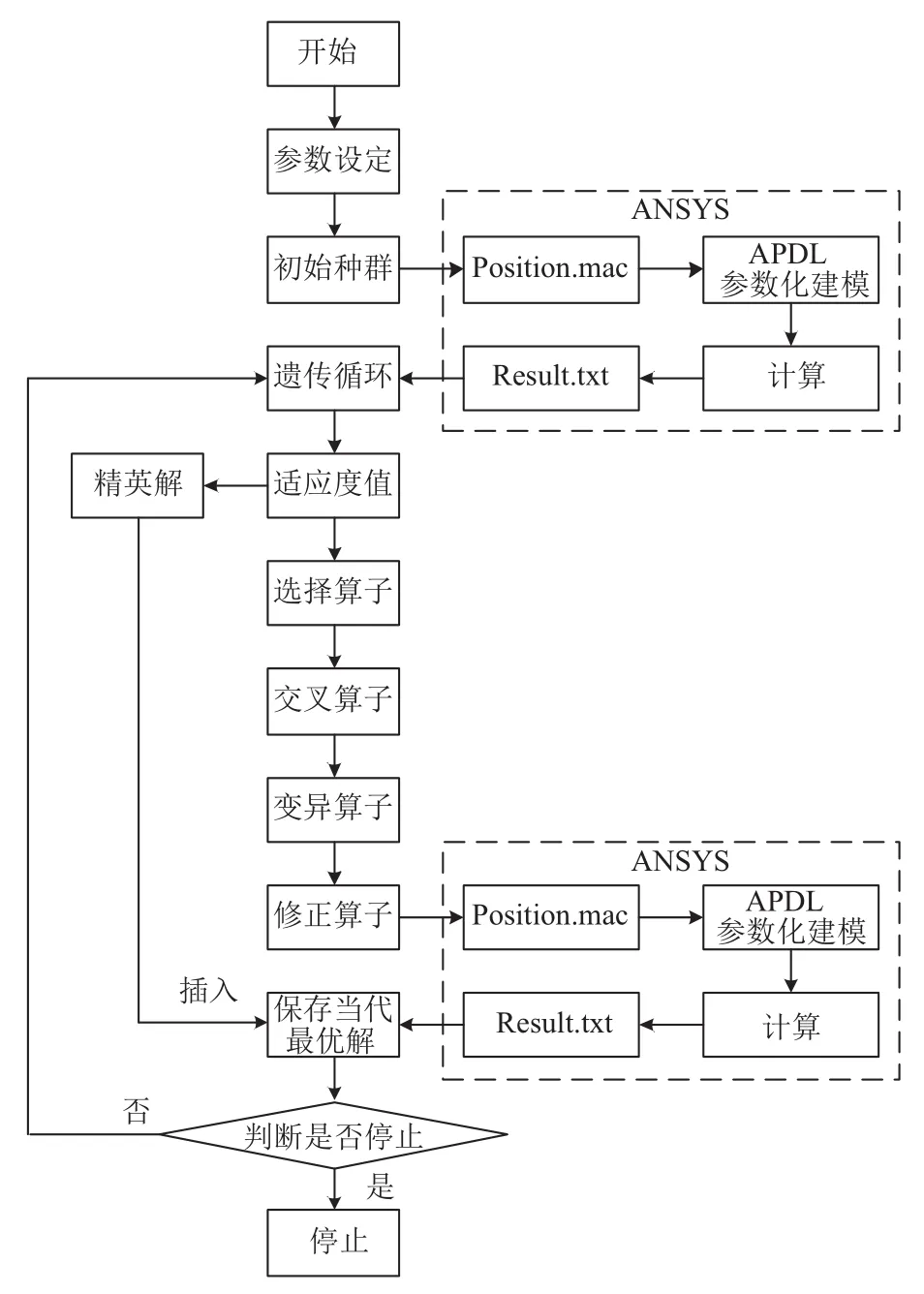
图6 改进的遗传算法流程图
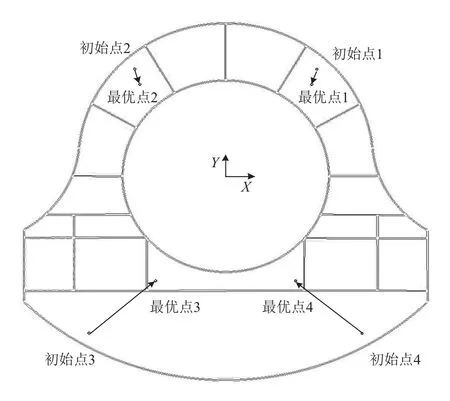
图7 最优的支撑序列
(2) 选择种群分别为40、60、80、100进行试验,优化过程迭代图如图8所示. 由此可见, 该算法收敛速度快, 平均在25代左右收敛, 具有较好的优化效率. 优化运行过程中, 外部调用的有限元软件未出现因不可行解而计算失败的问题. 相比静态、动态惩罚函数法,各方法在初代种群完成第一代遗传操作后可行解的平均个数(50次独立仿真)如图9所示. 由此可得, 该算法具有较好的稳定性.

图8 优化算法曲线图
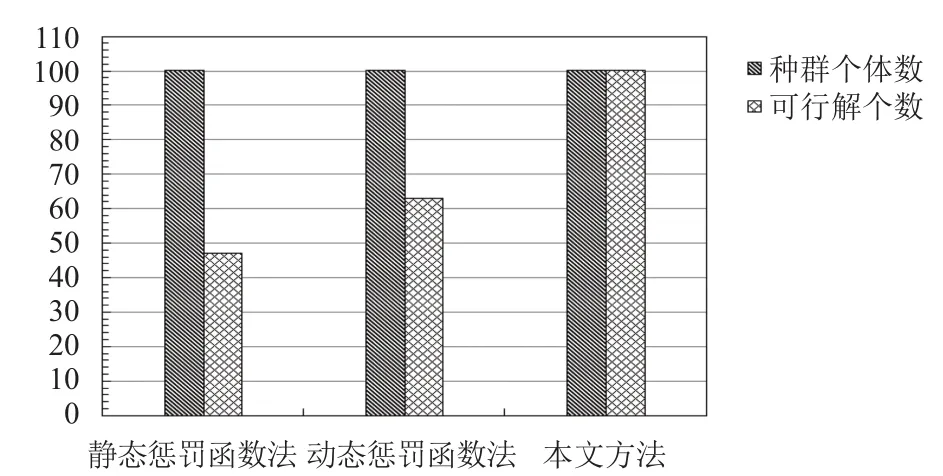
图9 不同算法可行解个数对比
(3) 对比优化前后框件的形变云图(如图10)可知,优化算法将支撑点靠近加强筋布置密集的部位, 使框内产生较大形变的部位转移到了加强筋布置密集的地方, 这样能够使加强筋承担更多的载荷, 在保证整体最大形变量显著减小的同时, 减小装配过程中需要铆接的部位(即边缘部位)的形变误差, 从而保证铆接的精度.
(4) 本文针对工艺特征约束在狭义层面的体现(即加强筋、不规则边缘、干涉情况约束等), 分析并建立了工艺约束在广义层面上的约束数学模型(如式(1)所示),考虑了约束的所有类型(即等式约束、不等式约束、不连续定义区间约束、离散定义域约束). 因此, 本文提出的修补算法和改进的遗传算法具有较广泛的适用性, 能用于所有包含等式、不等式、离散定义区间和定义域的约束优化问题. 如图11所示, 本文的改进遗传算法用于机身前端框件的案例, 该框件具有更复杂的不规则边缘. 由形变云图可见, 本文的改进遗传算法适用于此零件, 该框件在优化后的支撑序列下的形变量得到了改善.
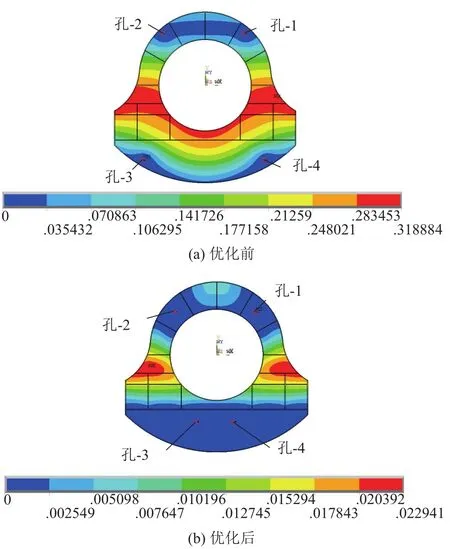
图10 优化前后形变量云图

图11 机身前端框件优化前后形变量云图
4 结论
(1) 本文将飞机机身框件因变形而引起的柔性定位误差作为优化目标, 建立相应的优化数学模型, 对可重构工装的支撑序列进行优化. 框的形变误差减小93.08%, 提升了可重构柔性工装在飞机装配中的精度,推进了先进可重构柔性工装在制造领域的应用.
(2) 从实际工程问题出发, 针对框的支撑/定位序列优化中的工艺特征约束, 提出一种修补算法, 并基于该算法改进遗传算法. 改进的遗传算法保证了种群中个体导入有限元分析软件中运行的可行性, 保证了优化算法的稳定性, 有效地弥补了其他约束处理技术在处理工艺特征约束问题时的缺陷.
(3) 从工艺特征约束的本质出发, 建立工艺特征约束的广义数学模型, 基于数学模型提出修补算法及改进的遗传算法, 具有一定通用性, 能够用于其他约束优化问题.
1冯子明, 邹成, 刘继红, 等. 飞机关键装配特性的识别与控制. 计算机集成制造系统, 2010, 16(12): 2552–2556.
2齐振超, 张开富, 李原, 等. 大型壁板自动钻铆定位误差分析与优化. 航空学报, 2015, 36(10): 3439–3449.
3郭飞燕, 王仲奇, 康永刚, 等. 飞机立柱式柔性工装定位误差分析与精度保障. 计算机集成制造系统, 2013, 19(8):2036–2042.
4王勇, 蔡自兴, 周育人, 等. 约束优化进化算法. 软件学报,2009, 20(1): 11–29.
5MEZURA-MONTES E, Coello CAC. Constraint-handling in nature-inspired numerical optimization: Past, Present and Future. Swarm and Evolutionary Computation, 2011, 1(4):173–194. [doi: 10.1016/j.swevo.2011.10.001]
6KRAMER O. A review of constraint-handling techniques for evolution strategies. Applied Computational Intelligence and Soft Computing, 2010, (11): 1–11.
7BARBOSA HJC, LEMONGE ACC: An adaptive penalty method for genetic algorithms in constrained optimization problems. INTECH: Open Access Publisher, 2008: 9–34.
8HO PY, SHIMIZU K. Evolutionary constrained optimization using an addition of ranking method and a percentage-based tolerance value adjustment scheme. Information Sciences,2007: 2985–3004.
9DEB K, SRIVASTAVA S. A genetic algorithm based augmented Lagrangian method for constrained optimization.Computational Optimization and Applications, 2012, 53(3):869–902. [doi: 10.1007/s10589-012-9468-9]
10MONTEMURRO M, VINCENTI A, VANNUCCI P. The automatic dynamic penalisation method(ADP) for handling constraints with genetic algorithms. Computer Methods in Applied Mechanics and Engineering, 2013, 256: 70–87. [doi:10.1016/j.cma.2012.12.009]
11王俊年, 刘云连, 伍铁斌. 改进的约束优化多目标遗传算法及工程应用. 计算机工程与应用, 2015, 51(3): 247–253.
12TAKAHAMA T, SAKAI S. Constrained optimization by applying the α constrained method to the nonlinear simplex method with mutations. IEEE Trans. on Evolutionary Computation, 2005, 9(5): 437–451. [doi: 10.1109/TEVC.2005.850256]
13林丹, 李敏强, 寇纪淞. 基于遗传算法求解约束优化问题的一种该算法. 软件学报, 2001, 12(4): 628–632.
14王晓圆, 王爱民, 范瑞城, 等. 基于遗传算法的配作齐停类调度约束处理技术. 计算机集成制造系统, 2014, 20(11):2788–2797.
15甘敏, 彭辉, 王勇. 多目标优化与自适应惩罚的混合约束优化进化算法. 控制与决策, 2010, 25(3): 378–382.
16ZHANG C, LI X, GAO L, et al. An improved electromag-Lnetism-like mechanism algorithm for constrained optimization. Expert Systems with Applications, 2013, 40(14): 5621–5634. [doi: 10.1016/j.eswa.2013.04.028]
17李维亮, 杨京京, 周良明. 基于模块化设计的柔性装配工装关键技术研究. 机床与液压, 2016, 44(4): 14–17.
18郭飞燕, 王仲奇, 康永刚, 等. 基于坐标孔的翼肋柔性装配协调方法. 中国机械工程, 2014, 25(24): 3271–3277. [doi:10.3969/j.issn.1004-132X.2014.24.002]
19田威, 廖文和, 唐金成. 面向复杂产品装配的柔性工装共性技术研究. 中国机械工程, 2010, 21(22): 2699–2704.
20张洪双, 蒋君侠, 柯映林, 等. 用于大部件调姿的数控定位器布局及行程优化. 计算机集成制造系统, 2013, 19(11):2742–2747.
21金栋平, 纪斌. 机翼后缘柔性支撑结构的拓扑优化. 航空学报, 2015, 36(8): 2681–2687.
22盖宇春, 朱伟东, 柯映林. 大型飞机总装配中支撑点设计分析技术. 浙江大学学报(工学版), 2013, 47(12): 2176–2183.
23XIONG L, MOLFINO R, ZOPPI M. Fixture layout optimization for flexible aerospace parts based on selfreconfigurable swarm intelligent fixture system. International Journal of Advanced Manufacturing Technology, 2013,66(9-12): 1305–1313. [doi: 10.1007/s00170-012-4408-5]
24LU C, ZHAO H W. Fixture layout optimization for deformable sheet metal workpiece. The International Journal of Advanced Manufacturing Technology, 2015, 78(1): 85–98.
Improved Genetic Algorithm Based on Process Constraint
ZHANG Jie, SHEN Jian-Xin, TIAN Wei
(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
To improve the accuracy and eliminate the error of aircraft assembly, the fixture layout for aircraft frame component with complicated process feature is optimized. In terms of process constraints, a generalized mathematical model of constraints is constructed and a theoretical repairing method is proposed. Additionally, an improved Genetic Algorithm is proposed based on the repairing method. In the example of fixture layout optimization of reconfigurable flexible fixture for frame component, the improved algorithm performed stably and the flexible position error, as a consequence, had reduced dramatically, at around 93.08%. The theoretical analysis and simulation result show that the improved Genetic Algorithm adapts to various kinds of constraint optimization and is feasible for its fast convergence rate and stability.
assembly precision; Genetic algorithm; constraint optimization; repairing method; process constraint; aircraft assembly
张节,沈建新,田威.基于工艺特征约束的改进遗传算法.计算机系统应用,2017,26(7):245–251. http://www.c-s-a.org.cn/1003-3254/5846.html
国家科技重大专项(2014ZX04001071)
2016-10-31; 收到修改稿时间: 2016-12-05

