基于互信息的加权朴素贝叶斯文本分类算法①
武建军, 李昌兵
(重庆邮电大学, 重庆 400065)
基于互信息的加权朴素贝叶斯文本分类算法①
武建军, 李昌兵
(重庆邮电大学, 重庆 400065)
文本分类是信息检索和文本挖掘的重要基础, 朴素贝叶斯是一种简单而高效的分类算法, 可以应用于文本分类. 但是其属性独立性和属性重要性相等的假设并不符合客观实际, 这也影响了它的分类效果. 如何克服这种假设, 进一步提高其分类效果是朴素贝叶斯文本分类算法的一个难题. 根据文本分类的特点, 基于文本互信息的相关理论, 提出了基于互信息的特征项加权朴素贝叶斯文本分类方法, 该方法使用互信息对不同类别中的特征项进行分别赋权, 部分消除了假设对分类效果的影响. 通过在UCIKDD数据集上的仿真实验, 验证了该方法的有效性.
朴素贝叶斯; 文本分类; 互信息; 加权; 特征项
随着互联网的不断发展, 互联网已经渗透到各行各业中, 而伴随着电子商务、自媒体、社交网络等概念和技术的出现和发展, 互联网每天都会产生巨大的信息, 大数据时代已经到来. 在这些信息中主要是文本数据, 如何对这些数据进行管理, 并进行分析和文本挖掘已成为一个重要的研究领域.
文本分类是对文本进行分析和挖掘的基础. 分类任务就是通过学习得到一个目标函数, 即分类模型y=f(x), 通过此分类模型把每个属性集x映射到一个预先定义的分类标签y[1]. 文本分类是在预定义的分类体系下, 根据文本的内容得到文本的特征项, 并将给定文本与一个或多个类别相关联的过程[2]. 文本自动分类可以很好的地解决大量文本信息自动归类的问题, 并可以应用于邮件过滤、文献组织、文本识别等领域. 因此, 对文本分类的研究具有重要的理论意义和实用价值.
朴素贝叶斯分类方法基于“属性独立性假设”, 是一种基于概率统计的分类方法, 适合于处理属性个数较多的分类任务, 而文本分类正是这种多属性的分类任务, 因此朴素贝叶斯成为文本分类的一种常用分类方法. 朴素贝叶斯分类方法不仅简单有效, 而且其性能在某些领域中表现得很好[3,4], 成为文本分类算法的重点研究对象之一.
朴素贝叶斯分类假定属性之间是相互独立的且重要性相同. 但是, 现实中这种假设通常是不成立的. 为了保证其分类效果, 许多学者对改进朴素贝叶斯分类器的属性加权方法做了一些尝试, 继Ferreira[5]提出属性加权的模型架构之后, Zhang[6]提出了基于增益比的属性加权方法, 邓维斌[7]提出了一种基于粗糙集的属性加权方法, Hall[8]提出了一种基于决策树的属性加权方法, ANGLEY[9]提出了一种基于属性删除方法的选择贝叶斯分类器(Selective NaÏve Bayesian, SNB),ARRY[10]提出了加权朴素贝叶斯(Weighted NaÏve Bayes, WNB)模型, 即根据属性的重要程度给不同属性赋不同权重的, 并通过实验发现它们能改进朴素贝叶斯的分类效果[9,10]. 但是这些都是对朴素贝叶斯算法的改进, 没有考虑贝叶斯算法应用到文本分类中的情况.
本文通过对文本分类的研究, 利用互信息的理论,研究如何使用属性加权来改进朴素贝叶斯算法, 在文本分类中, 通过使用特征项相对于类别的互信息作为特征项权重, 提出了基于互信息的特征项加权朴素贝叶斯文本分类算法, 以消除属性重要性相等的假设对分类效果的影响, 提高朴素贝叶斯文本分类算法的分类效果.
1 互信息的相关概念
文本分类时首先要对待分类的文本进行预处理,提取特征项. 在预处理过程中, 因为一篇文章提取出的特征项往往非常多, 而很多词是对表达该文章是无意义的, 需要做降维处理, 特征选择和特征提取[11,12]是两类主要的特征项降维的方法. 互信息(MI)是一种特征选择算法, 用来表征两个变量之间的相关性. 特征项w和类别Cj之间的互信息MI(w, Cj)定义如下:

P(w)表示特征项w在整个训练集出现的概率,P(Cj)表示训练集中Cj类文档出现的概率, P(w, Cj)表示类别Cj中含有特征项w的概率.
当w和类别Cj无关时, 互信息为0;当特征项的出现依赖于某个类别时, 该特征项与该类别的MI 值就会很大;当特征项在某个类别很少出现时, 它们的MI值会很小, 甚至为负数. 通过设定互信息的阈值, 可以实现对特征项的选择, 从而实现特征项降维处理.
2 朴素贝叶斯分类算法
朴素贝叶斯分类算法基于贝叶斯公式. 它的基本原理是: 在已知类的先验概率和该类中每个属性所有取值的条件概念的情况下, 可以计算出待分类样本属于某个类别的条件概率, 从中选择条件概率最大的作为该样本的分类.
假设共有m个类, C={C1, C2, …, Cm}, j=1, 2, …, m,以P(Cj)表示Cj类发生的先验概率, 且P(Cj)>0. 对于任一文档di={w1, w2, …, w|V|}, i=1, 2, …, l, 其中, wk为特征项, k=1, 2, …, |V|, |V|为特征项总个数, Cj类中di条件概率是P(di|Cj), 则计算文档di属于Cj类的后验概率为:
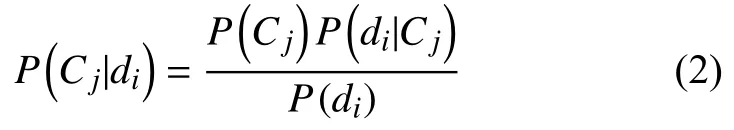
由于P(di)是一个常数, 并且基于属性独立性假设P(d|C)=P(w1|C)P(w2|C)…P(wn|C), 故有:
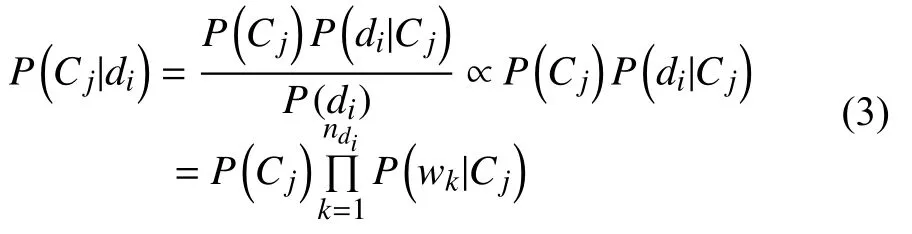
P(wk|Cj)是特征项wk出现在Cj类中的后验概率,ndi是文档di中特征项的个数. 朴素贝叶斯分类的目标是寻找“最佳”的类别. 最佳类别是指具有最大后验概率(maximum a posteriori -MAP)的类别cmap:
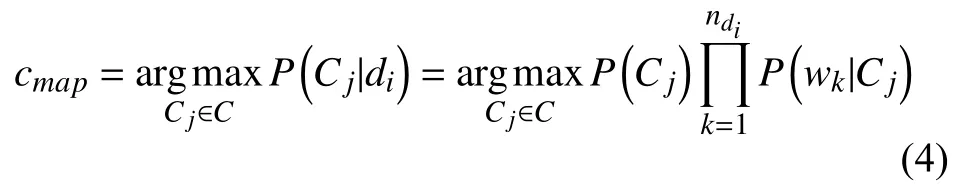
其中, Cj类的先验概率P(Cj)可以通过公式P(Cj)=Ncj/N取得, Ncj表示训练集中Cj类中的文档数目, N表示训练集中所有文档数据. P(wk|Cj)可以通过以下公式得出:
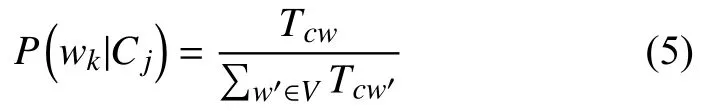
Tcw是训练集中类别Cj中的特征项wk的次数 (多次出现要计算多次),是类别Cj中所有特征项出现的总次数. 为了避免零概率问题, 需要对上述公式进行平滑处理:

|V|为不同特征项的个数.
由于很多小概率的乘积会导致浮点数下溢出, 可以通过取对数将原来的乘积计算变成求和计算, 对应的公式为:
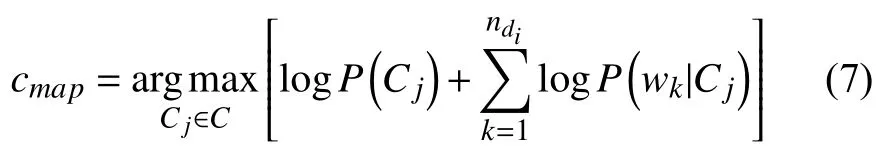
3 加权朴素贝叶斯分类算法
朴素贝叶斯认为所有特征项对于文档的分类重要性都是一致的, 但现实中每个特征项的重要性是不一样的. 因此, 可以根据特征项的重要程度给不同的特征项赋不同的权值, 即加权朴素贝叶斯分类算法, 其模型为:
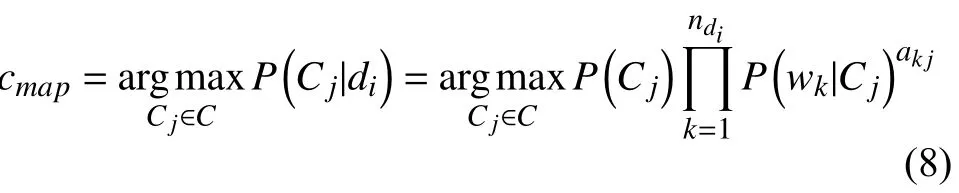
ak,j表示特征项wk在Cj类中的权重. 属性的权值越大, 该属性对分类的影响就越大. 其对数形式为:
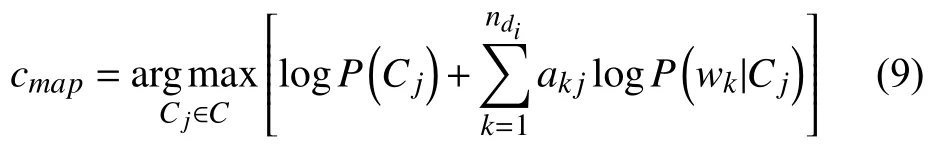
4 特征项加权的朴素贝叶斯分类算法
在实际情况中, 特征项与类别之间必然存在某种关联关系, 而朴素贝叶斯算法为了简化计算过程, 忽略了这种关联, 降低了分类的效果. 可以通过某种方式量化特征项与类别之间的关联关系, 以此值作为该特征项出现在类中条件概率的权值, 以反映不同特征项的重要程度, 这样有利于提升朴素贝叶斯的分类效果.
互信息MI作为一种特征选择的算法, 用来表示特征项w和类别c之间相关性. 用互信息MI作为后验概率P(wk|Cj)的权重非常合适, 因为与类别相关性大的特征项, 其权重就应该更大一些;当特征项与类别不相关时, MI为0, 表示该特征项的后验概率P(wk|Cj)对分类不起作用;当特征项很少出现在某个类别时, MI是负数,表示该特征项是噪声, 对分类产生了负作用. 使用互信息MI作为权重, 体现了不同特征项的对分类的作用不同, 在很大程度上消除了属性独立性假设对分析产生的影响, 使分类效果更好. 根据互信息的计算过程, 特征项wk对类别Cj的权重可以表示为:
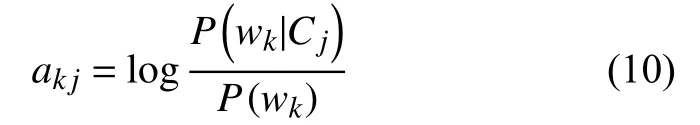
代入公式9得到加权的朴素贝叶斯算法:
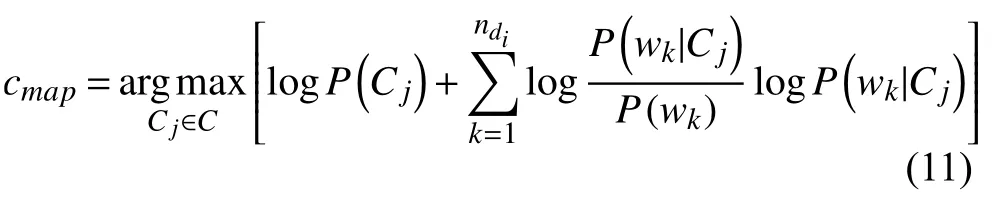
Cj类的先验概率P(Cj)以及特征项wk出现在Cj类中的后验概率P(wk|Cj)前面已经给出了计算公式, 而P(wk)表示特征项wk的先验概率, 可以通过以下公式得出:

Tw是训练集中特征项wk在所有类别中出现的次数(多次出现要计算多次),是训练集中所有特征项出现的总次数. 为了避免零概率问题, 需要对上述公式进行平滑处理:
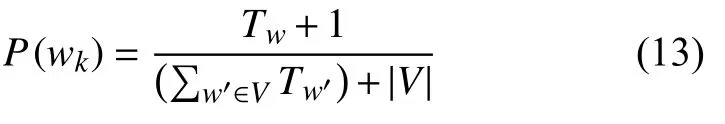
|V|为训练集中不同特征项的个数.
为了建立特征项加权朴素贝叶斯分类器, 首先需要利用训练样本进行模型训练, 通过计算得到每个特征项的条件概率及其权重, 然后通过测试样本对建立的模型进行验证. 分类器的实现步骤如下:
步骤1. 数据预处理: 将训练样本和待分类样本进行分词、去停用词.
步骤2. 文本向量化: 把文本转换为VSM(向量空间模型), 文本di表示为一个空间向量: di={w1, w2, …,w|V|}, i=1, 2, …, l, 其中, wk为特征项, k=1, 2, …, |N|,|N|为特征项总个数.
步骤3. 特征选择: 计算每个特征项wk与每个类别Cj的互信息MI, 并根据MI值进行特征选择, 得到一个MI矩阵:
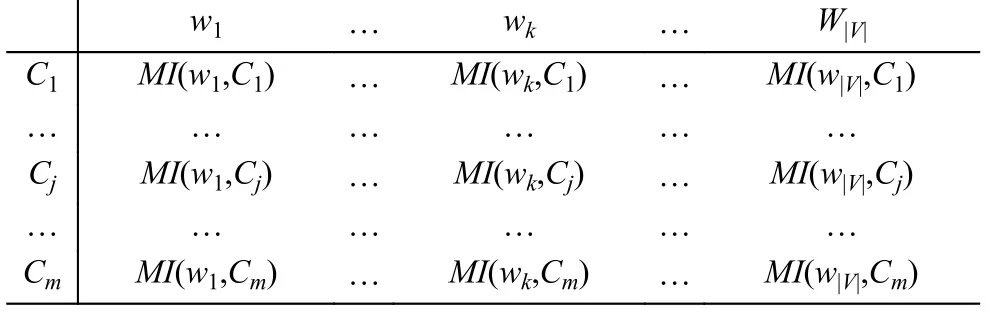
其中MI(wk, Cj)表示特征项wk与类别Cj的互信息.
步骤4. 分类器构造:
步骤4.1 扫描所有训练样本, 统计训练集中文档总数, 每个类别文档总数, 每个特征项在每个类别出现的次数, 以及不同特征项的个数, 形成统计表.
步骤4.2 计算每个类别Cj的先验概率P(Cj), 得到先验概率向量P(C){P(C1), P(C2), …, P(Cm)}
步骤4.3 计算每个特征项wk出现在Cj类中的后验概率P(wk|Cj), 得到后验概率矩阵:

步骤4.4 根据互信息计算得到后验概率P(wk|Cj)的权重, 得到权重矩阵:
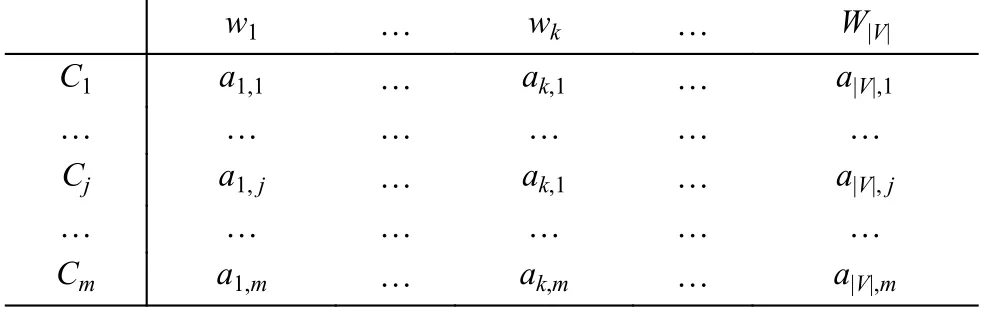
5 特征项加权的朴素贝叶斯分类算法
实验采用的数据是来源于UCI KDD Archive的20个Newsgroup英文文本数据集, 大小约为44.5M. 数据集中包括20个不同的新闻组, 共20000篇文档, 涉及的领域有政治、宗教、体育、科学、医药、电子、计算机等.
选取其中的10类作为实验数据: alt.atheism、comp.graphics、comp.sys.ibm.pc.hardware、misc.forsale、rec.motorcycles、rec.sport.baseball、sci.electronics、sci.space、talk.politics.guns、talk.politics.mideast, 为了方便实验结果分析的表述, 依次简记为L1、L2、L3、L4、L5、……、L10. 其中每类文件包含1000篇文档,共10000篇文档. 将数据集平均分成5份, 首先用其中4份作为训练样本, 1份作为测试样本. 使用训练样本通过训练过程得到贝叶斯概率矩阵及特征项权重矩阵,然后调用加权朴素贝叶斯文本分类算法对测试样本进行测试, 依次轮回, 采用不同的训练样本和测试样本做5次实验, 取其平均值. 分别用朴素贝叶斯算法(NB)和特征项加权贝叶斯文本分类算法(TWNB)进行测试.
实验使用了数据挖掘平台Weka, Weka是怀卡托智能分析环境(waikato envimnment for knowledge analysis), 是由新西兰怀卡托大学开发的基于Java环境的、开源的机器学习及数据挖掘软件[13,14], 本实验主要是利用Weka的二次开发功能, 编写了加权朴素贝叶斯文本分类算法, 并使用Weka进行数据的准备、模型建立和模型验证过程. 实验的数据虽然是英文文档, 但是还是需要进行数据的预处理包括分词、粗降维等, 得到Weka需要的数据格式, 如{People in the San Francisco Bay area can get Darwin Fish from Lynn Gold}, 即每个文档包含该文档所有单词, 并以空格分隔, 每个不同类别的所有文档放在以类别名称命名的文件夹. 在数据预处理过程中采用了分词软件包IKAnalyzer, IK Analyzer是一个开源的, 基于java语言开发的轻量级的中文分词工具包[15], 支持中文和英文的分词. 在IKAnalyzer的基础上编写了数据预处理程序Splitword, 实现了分词、粗降维等过程.
测试步骤如下:
步骤1. 对所有样本文件进行分词, 对分词后的文本进行粗降维, 即将停用词, 低频词从文档中去除.
步骤2. 在Weka的Simple CLI中运行命令: java weka.core.converters.TextDirectoryLoader -dir e:/data >e:data.arff, 所有训练样本和测试样本存在e:/data文件夹下, 执行完后生成Weka的数据格式为data.arff.
步骤3. 通过weka.filters.unsupervised.attribute.String To Word Vector类, 将文本转化为文本向量形式,并使用weka.filters.supervised.attribute.Attribute Selection类, 进行特征选择.
步骤4. 使用训练样本通过计算得到加权贝叶斯文本分类模型, 即贝叶斯概率矩阵和特征项权重矩阵.
步骤5. 使用测试样本对模型进行测试, 测试采用Cross-validation方式, Folds设置为5, 得到测试结果, 与贝叶斯算法进行比较.
通过精确率(Precision)、召回率(Recal1)、F1测试值3项主要指标进行评估测试, 实验结果如表1所示.
为了直观的反映实验结果, 将上面的实验结果使用图来表示, 如图1所示.
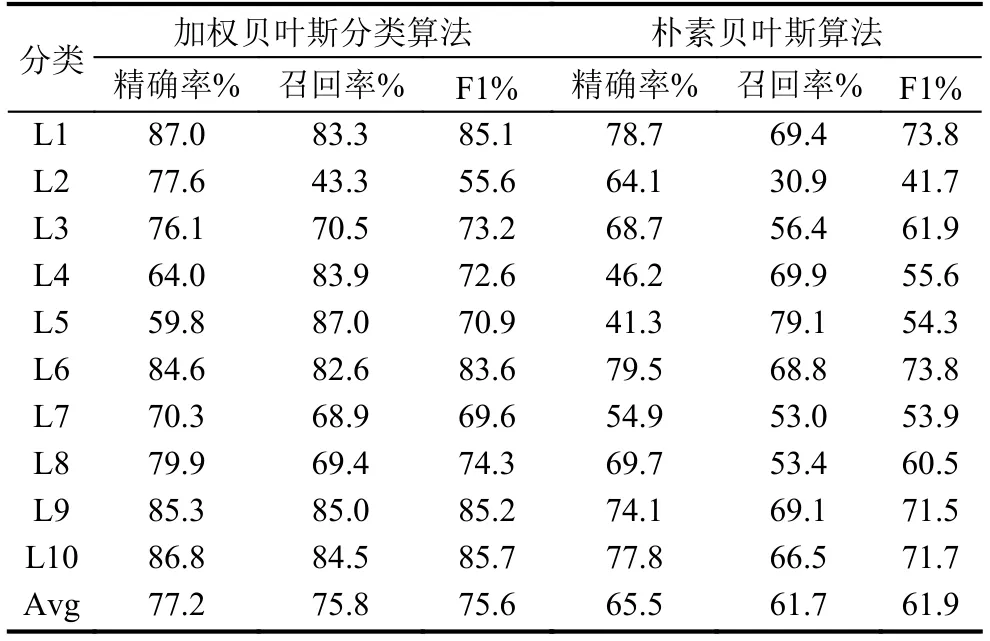
表1 实验结果
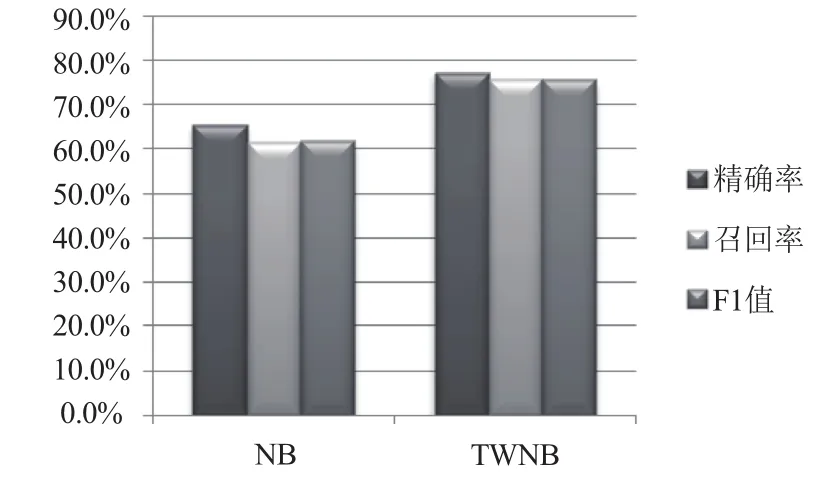
图1 实验结果
从上面的实验结果可以得出以下结论:
1)使用互信息进行加权的贝叶斯分类算法的分类效果明显高于贝叶斯算法.
2)当文档特征项比较多时, 加权的贝叶斯分类算法的优势更加明显.
6 总结
传统朴素贝叶斯分类方法有精度较高、分类性能较好、时间复杂度低等优点, 但其特征项独立性假设及特征项重要性相等假设通常与现实不符, 这影响了它的分类效果. 本文根据文本分类的特点, 采用互信息来计算各个特征项的权重, 提出了基于互信息的加权朴素贝叶斯文本分类算法. 以UCI KDD Archive的10个Newsgroup英文文本数据集为测试数据, 通过实验比较了朴素贝叶斯算法、特征项加权贝叶斯算法的分类效果. 实验表明:本文所提出的方法可以部分去除朴素贝叶斯分类算法特征项独立性假设及特征项重要性相等假设, 提高朴素贝叶斯的文本分类效果.
1Tan PN, Steinbach M, Kumar V. 数据挖掘导论. 第2版. 范明, 范宏建, 译. 北京: 人民邮电出版社, 2011.
2宗成庆. 统计自然语言处理. 第2版. 北京: 清华大学出版社, 2013.
3Agrawal R, Imielinski T, Swami A. Database mining: A performance perspective. IEEE Transactions on Knowledge and Data Engineering, 1993, 5(6): 914–925. [doi:10.1109/69.250074]
4Friedman N, Geiger D, Goldszmidt M. Bayesian network classifiers. Machine Learning, 1997, 29(2): 131–163.
5Ferreira JTAS, Denison DGT, Hand DJ. Weighted naive bayes modelling for data mining. London, UK: Deparment of Mathematics, Imperial College, 2001. 454–460.
6Zhang H, Sheng SL. Learning weighted naive Bayes with accurate ranking. Proc. of the 4th IEEE International Conference on Data Mining. Brighton, UK. 2004. 567–570.
7邓维斌, 王国胤, 王燕. 基于Rough Set的加权朴素贝叶斯分类算法. 计算机科学, 2007, 34(2): 204–206.
8Hall M. A decision tree-based attribute weighting filter for naive bayes. Knowledge-Based Systems, 2007, 20(2):120–126. [doi: 10.1016/j.knosys.2006.11.008]
9Langley P, Sage S. Induction of selective Bayesian classifiers. Proc. of the 10th International Conference on Uncertainty in Artificial Intelligence. Seattle, USA. 1994.399–406.
10Zhang H, Sheng SL. Learning weighted naive bayes with accurate ranking. Proc. of the 4th IEEE International Conference on Data Mining. Brighton, UK. 2004. 567–570.
11Pinheiro RHW, Cavalcanti GDC, Correa RF, et al. A globalranking local feature selection method for text categorization.Expert Systems with Applications, 2012, 39(17): 12851–12857. [doi: 10.1016/j.eswa.2012.05.008]
12奉国和, 郑伟. 文本分类特征降维研究综述. 图书情报工作, 2011, 55(9): 109–113.
13Witten IH, Frank E. 数据挖掘: 实用机器学习技术. 第2版.董琳, 邱泉, 于晓峰, 译. 北京: 机械工业出版社, 2006.
14WEKA官方网站. http://weka.wikispaces.com/.
15开源中国社区. http://www.oschina.net/p/ikanalyzer/.
Mutual Information-Based Weighted Naive Bayes Text Classification Algorithm
WU Jian-Jun, LI Chang-Bing
(Chongqing University of Posts and Telecommunications, Chongqing 400065, China)
Text classification is the foundation of information retrieval and text mining. Naive Bayes can be applied to text classification as it is simple and efficient classification. But the two assumption about Naive Bayes algorithm that its attribute independence is equal to its attribute importance are not always consistent with the reality, which also affects the classification results. It is a difficult problem to disapprove the assumptions and improve the classification effect.According to the characteristics of text classification, based on text mutual information theory, a Term Weighted Naive Bayes text classification method based on mutual information is proposed, which uses the mutual information method to weight the feature in different class. The effect of two assumptions on classification is partially eliminated. The effectiveness of the proposed method is verified by the simulation experiment on the UCI KDD data set.
Naive Bayes; text classification; mutual information; weighted; term
武建军,李昌兵.基于互信息的加权朴素贝叶斯文本分类算法.计算机系统应用,2017,26(7):178–182. http://www.c-s-a.org.cn/1003-3254/5840.html
国家自然科学基金(61472464); 重庆市基础与前沿研究计划项目(cstc2013jcyjA40017)
2016-10-14; 收到修改稿时间: 2016-12-01

