多重超平面完备残差图
段辉明,邵凯亮,张清华,曾 波
(1.重庆邮电大学理学院,重庆 400065)(2.重庆工商大学商务策划学院,重庆 400067)
多重超平面完备残差图
段辉明1,邵凯亮1,张清华1,曾 波2
(1.重庆邮电大学理学院,重庆 400065)(2.重庆工商大学商务策划学院,重庆 400067)
本文研究了任意维超平面完备残差图和多重超平面完备残差图,将Erd¨os、Harary和Klawe’s定义的平面残差图推广到任意维超平面.利用容斥原理以及集合的运算性质等方法,获得了任意维超平面完备残差图的最小阶和唯一极图,以及任意维超平面完备残差图的一个重要性质,同时获得了多重任意维超平面完备残差图的最小阶和唯一极图.
残差图;邻域;同构;独立集
1 引言
2 预备知识
定义2.1设图G=(V,E),u∈V=V(G),集合N(u)={x|x∈V(G),x与u邻接}与N∗(u)={u}∪N(u)分别叫做顶点u的邻域和闭邻域.
定义2.2设F是一个给定的图,如果对每一个顶点u∈V(G),从G中减去u的闭邻域N∗(u)得到的图与F同构[10-11],则称图G为F-残差图.递归地,定义G是m-F-残差图为,如果对于任意u∈V(G),G-N∗(u)得到的图都是(m-1)-F-残差图.当然1-F-残差图简单地叫做F-残差图.
定义2.3图G是r-1维超平面完备图,如果x∈V(G),V(G)=V1×V2×···×Vr,其中x={ (x1,x2,···,xr)|xi∈Vi,i=1,2,···,r},|Vi| =ni,i=1,2,···,r, 两个顶点x=(x1,x2,···,xr) 和y=(y1,y2,···,yr) 相邻当且仅当x/y,存在某个k=1,2,···,r,xk=yk.为方便起见,本文用HPK(n1,n2,···,nr)代替r-1维超平面完备图.
定义2.4设G1=(V1,E1),G2=(V2,E2)是两个图,G1与G2合成G=G1[G2],定义为V(G)=V1×V2={x=(x1,x2)| (x1∈V1,x2∈V2},两个顶点u=(u1,u2)和v=(v1,v2)是相邻的当且仅当u1与v1在G1相邻,或者u1=v1,u2与v2在G2中相邻.
定义2.5令G=(V,E),S⊂V=V(G),若S不存在两个点x,y∈S在G中邻接,而且|S|=k,则称S为G中的k-独立集.
定义2.6设图G1=(V1,E1),G2=(V2,E2),定义G=G1+G2,其中V(G)=V1∪V2,E(G)=E1∪E2∪E[K(V1,V2)],这里K(V1,V2)是以V1与V2为独立点集的完备二部图.
下面是文献[1]中的一个重要结论.
引理2.1[1]设G是F-残差图,则d(u)=ν(G)-ν(F)-1,∀u∈V(G),其中ν(G)是G的阶.
文中没有定义的术语与符号参阅文献[1-8].
3 任意维超平面完备残差图的最小阶和唯一极图
由定义2.3可以直接得到下面引理.
引理3.1若G是HPK(n1,n2,···nr)-残差图,n1,n2,···nr≥r≥3,则对任意两点u,v∈V(G),存在一点w∈G,使得u,v∈V(G)-N∗(w).
对于任意维超平面残差图还有以下结论.
引理3.2若(n1+1,n2+1,···,nr+1),n1,n2,···,nr≥ 1,r≥ 2,则G是HPK(n1,n2,···,nr)-残差图.
证令V(G)=V1×V2×···×Vr,|Vi| =ni+1,点x=(x1,x2,···xr)与y=(y1,y2,···,yr)彼此不相邻,定义为xi/yi,i=1,2,···,r,因此对于任意一点v=(v1,v2,···,vr)∈G,则有

引理3.3若G=HPK(n1,n2,···nr),{v1,v2,···,vr,v0} 是G的r+1 独立集,则有

证假设存在点x=(x1,x2,···,xr)∈N∗(v1)∩N∗(v2)∩···∩N∗(vr)∩N∗(v0),并且与,k=0,1,···,r邻接,由G的邻接条件可知,存在一点,所以有1≤ik≤r,k=0,1,···,r,ik=il=h,k/=l,则一定存在k,l,使得,然而与在G中不邻接,从而导致矛盾.证毕.
引理3.4若H=HPK(n1+1,n2+1,···,nr+1),{v,v1,v2,···,vr} 是H的 (r+1)-独立集,且设Hi=H-N∗(vi),i=1,2,···,r,则有

证因为V(H)=V(Hi)∪N∗(vi),v∈V(Hi),所以

引理3.5如果HPK(n1,n2,···nr),{v1,v2,···,vk}⊂V(G),以及 {u1,u2,···,uk}⊂V(H)分别是G和H的k-独立集,则有

证对于任意k-独立集{v1,v2,···,vk}⊂V(G),这里把G的所有k-独立集定义为一个函数,记为gk,又假设gk=g(v1,v2,···,vk)=|N∗(v1)∩N∗(v2)∩ ···∩N∗(vk)| ,则gk是一个常值函数,因为当k=1时,
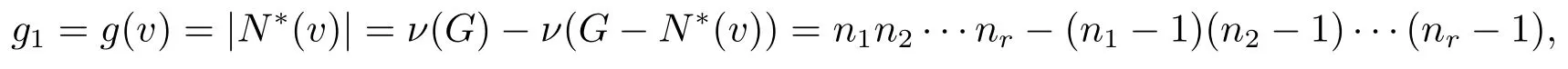
所以g1=g(v)为一个常数.类似地,可以证明gk是一个常数,且由引理3.3可得知当1<k<r+1 时,gk=0. 设Gk=G-N∗(v1)-N∗(v2)-···-N∗(vk),则有GkHPK(n1-k,n2-k,···,nr-k)和ν(Gk)=(n1-k)(n2-k)···(nr-k)=vk,因此有
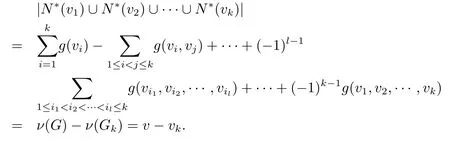
又由于,则存在一个映射σ:V(H)→V(G),u1和u2在H中邻接当且仅当σ(u1)和σ(u2)在G中彼此邻接. 假设vi=σ(ui),i=1,2,···,r,则有 {v1,v2,···,vk}⊂V(G)是一个k-独立集当且仅当{u1,u2,···,uk}⊂V(H)是k-独立集,因此

定理3.1若G是一个HPK(n1,n2,···,nr)-残差图,n1,n2,···,nr≥r≥3,则有ν(G)≥ (n1+1)(n2+1)···(nr+1).
证对于任意一点v∈G,有G-N∗(v)=(n1,n2,···,nr),记

点x=(x1,x2,···,xr)和y=(y1,y2,···,yr)在F中彼此不邻接定义为当且仅当xi/yi,i=1,2,···,r.设vk=(k,k,···,k),k=1,2,···,r,则有 {v,v1,v2,···,vr} 是G中的r+1-独立集.由引理3.4与3.5可知

因此

下面设H=HPK(n1+1,n2+1,···,nr+1),则有

因此有

证毕.
上面得到r-1维超平面残差图的最小阶,下面主要构造最小图,并证明此图是唯一的极图.为了得到极图,设G是一个HPK(n1,n2,···,nr)-残差图,n1,n2,···,nr≥r≥3,主要任务是命名G中点的名称以及点与点的邻接关系以及相应的命名规则.首先定义G中的点和邻接关系,设

定义点x=(x1,x2,···,xr) 与y=(y1,y2,···,yr) 彼此不相邻当且仅当xi/yi,i=1,2,···,r. 对任意一点u∈G, 则有G-N∗(u)=HHPK(n1,n2,···,nr). 下面定义H中的点

在H中定义两点不相邻与在G中的定义一致,由此可以根据(3.1)式定义G的任何一个子集.又由于H=G-N∗(v),要命名G中的点,首先命名N∗(v)中的点.设vk=(k,k,···,k),k=1,2,···,r,则有
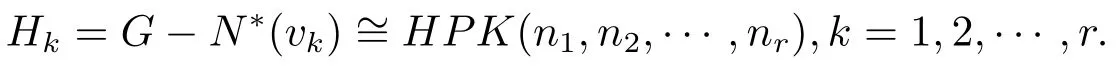
由引理3.4可得

再根据引理3.5可知

再由引理3.3知N∗(v)∩N∗(v1)∩···∩N∗(vr)=φ,所以(3.2)式最后一个并集的集合为空集,所以(3.2)式应为

为了命名G中的所有点,因为H=G-N∗(v)以及Hk=G-N∗(vk),故下面先命名N∗(vk)命名规则,设H=HPK(n1,n2,···,nr),n1,n2,···,nr≥r≥ 3,
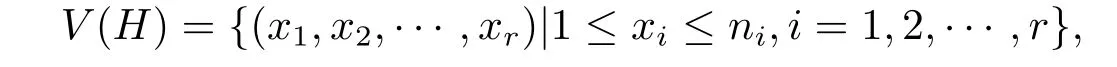
点x=(x1,x2,···,xr) 与y=(y1,y2,···,yr) 不相邻定义为当且仅当xiyi,i=1,2,···,r.设v=v1=(1,1,···,1),

则有下面命名规则.
命名规则 3.1R1:i1,i2,···,il,il+1,···,ir是 { 1,2,···,r}的一个排列,其中 1≤i1<i2<···<il≤r,1≤il+1<···<ir≤r,1≤l≤r-1.
R2:a1,a2,···,al是一个序列,其中 2≤ak≤nik,k=1,2,···,l.
R3:Y={ (y1,y2,···,yr)∈F1|yirak,k=1,2,···,l}.
R4:b1,b2,···,br是一个序列,其中 1≤bk≤nik,bkak,k=1,2,···,l.
R5:uk=其中,则有唯一点,满足
R6:x∗是与u1,u2,···,ul邻接的.
R7:x∗与Y中的点彼此不邻接.
下面说明命名规则 3.1 合理性,设x∗=(x1,x2,···,xr),xik=ak,k=1,2,···,l,xil+1=···=xir=1,这里点x∗是满足C6和C7这两条性质的,且这样的x∗是唯一的,因为x∗与Y中点是彼此不邻接的,因此有xil+1=···=xir=1.
下面需要证明的是xik=ak,x∗是不邻接y∈Y,xik仅仅只能为ak或者1,而这里xikbk,故有x∗与uk邻接的,以及xik=ak,k=1,2,···,l,命题规则是合理的.
检验N∗(v1)的点的关键条件是命名规则3.1中R1,R2,R3,由于b1,b2,···,bl选择是不唯一的,导致u1,u2,···,ul也是不唯一的,所以命名的关键主要是R1,R2,R3,因此这三个条件可以作为整个图G的命名条件,于是得到下面的命名规则.
命名规则3.2命名规则3.1中的R1,R2,R3可以唯一确定N(v1)中的每一个点,相反N∗(v1)中的所有的点如果都已经确定,则命名规则3.1中R1,R2,R3也相应被确定.
命名规则3.2的前部分可直接由命名规则3.1的说明得到,下面说明结论的后半部分.
设x=(x1,x2,···,xr)∈N(v1),根据N(v1)的点的性质,可以重新命名规则3.1中的R1,R2,R3.
R1:i1,i2,···,il,il+1,···,ir,1≤i1<i2<···<il≤r,1≤il+1<···<ir≤r,1≤l≤r-1,其中xil+1=···=xir=1,xi1,xi2,···,xi1/1.
R2:a1,a2,···,al是一个排列,其中ak=xik,2≤ak≤nik,k=1,2,···,l.
R3:Y={ (y1,y2,···,yr)∈F1|yikak,k=1,2,···,l}.
由此可以根据命名规则3.1和3.2命名所有的N∗(vk)中的点,其中vk=(k,k,···,k),k=1,2,···,r. 如果有NH(v) 的点x未命名,其中H=HPK(n1,n2,···,nr),n1,n2,···,nr≥r≥3,则可以任意找一点v∈H,根据H-N∗(v)中的点的命名规则命名,即可以根据命名规则3.1和3.2命名.对于N(v)中点的命名可以根据N∗(v)的点命名,只须设v=(0,0,···,0),所以N(v)的点的命名规则也被确定.
因为H=G-N∗(v),以及Hk=G-N∗(vk),要确定G中的点,最后剩下NHk(v)中的点没有命名规则,由式子(3.1),(3.3)可知首先命名NH1(v)中的点,有下面的命名规则.
命名规则3.3只需要把命名规则3.1和3.2中的1用0代替即可得到NH1(v)中的点的命名规则.

的点命名,即根据H=G-N∗(v)的点命名规则命名,只须把命名规则3.1和3.2中的1用0代替即可.
下面命名NH2(v)∩NH2(v1)的点.由于
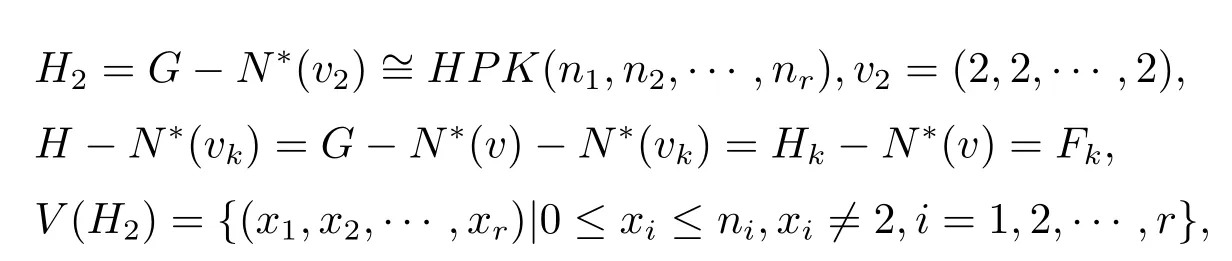
命名规则 3.4R1:i1,i2,···,il,il+1,···,ir一个排列.
R2:a1,a2,···,al是一个序列,其中 1≤ak≤nik,ak2,k=1,2,···,l,1∈{a1,a2,···,al}.
R3:Y={ (y1,y2,···,yr)∈F2|yik/ak,k=1,2,···,l}.
命名规则3.4只在命名规则3.2的R2增加了条件1∈{a1,a2,···,al},增加此条件的目的主要是保证条件R1,R2,R3确定的点x一定是属于.如果不增加此条件,根据图G的点的命名的唯一性原则,只能确定中的点x,增加此条件后在找一点x∗,而点x∗可以分别在H1与H2重新命名.
下面主要说明x∗在H1与H2的命名是一致的,前面命名规则3.4命名了H2中的点.下面先完成H1中的命名规则:x∗在H1命名为(x1,x2,···,xr).又由于x∗不邻接v2=(2,2,···,2)∈H1,因此在H1中的命名规则可以如下.
命名规则 3.5R1:i1,i2,···,il,il+1,···,ir是一个排列,其中xi1,xi2,···,xil0,1,2,xil+1=···=xil=0.
R2:a1,a2,···,al是一个序列,其中ak=xik0,1,2,k=1,2,···,l.
R3:Y={ (y1,y2,···,yr)∈F2|yik/ak,k=1,2,···,l}.
下面说明x∗在H1与H2中命名是一致的,假设在H2中有一点其中=ak,k=1,2,···,l以及=···==0且ak/0,1,2,因此x∗∗是与点v1=(1,1,···,1)∈H2不邻接的,而,从而x∗∗=x∗,故x∗在H1与H2中命名是一致的.
命名规则 3.6R1:i1,i2,···,il,il+1,···,ir是一个排列,其中xi1,xi2,···,xil/0,1,2,xil+1=···=xil=0.
R2:a1,a2,···,al是一个序列,其中 1≤at≤nit,at/k,以及 { 1,2,···,k-1}⊂{a1,a2,···,ak}.
R3:Y={ (y1,y2,···,yr)∈Fk|yitat,t=1,2,···,l}.
根据上面的命名规则可以确定x∗=(x1,x2,···,xr),且,由上面的结论,可设k=r,则可以得到式子(3.3)的最后一个式子命名规则.
命名规则 3.7R1:i1,i2,···,ir-1,ir是一个排列,且有1≤i1<i2<···<ir-1≤r,1≤ir≤r.
R2:a1,a2,···,ar-1是一个序列,其中 {a1,a2,···,ar-1}={ 1,2,···,r-1}.
R3:Y={ (y1,y2,···,yr)∈Fr|yik/ak,k=1,2,···,r-1}.
根据上面的命名规则R1,R2,R3,可以完全命名Hr,这里Hr=G-N∗(vk),前面定义了N∗(vk)的命名规则,这样G中的所有的点被Hr与N∗(vk)点完全决定,可以命名为V(G)={ (x1,x2,···,xr)| 0≤xi≤ni},G中的两点x=(x1,x2,···,xr) 和y=(y1,y2,···,yr) 彼此不邻接当且仅当xiyi,i=1,2,···,r.
根据上面的命名原则可以得到下面结论.
定理3.2若G是HPK(n1,n2,···,nr)-残差图,n1,n2,···,nr≥r≥ 3,ν(G)=(n1+1)(n2+1)···(nr+1),则(n1+1,n2+1,···,nr+1),且这样的G是唯一的.
证对于G中任意两点x和y,根据引理3.1可知,一定存在一点w,使得w与x和y都不邻接.假设w∈Hk,其中Hk是遵循上面的命名规则,对于任意一个k,如果既有x∈Hk也有y∈Hk,则可以使用Hk命名规则来命名.设H∗=G-N∗(w)(n1,n2,···nr),则有x,y∈H∗.因为G中的点可根据Hk中的点命名规则命名,又根据命名的唯一性可以命名G中所有的点,因为H∗=G-N∗(w),所以根据G命名规则命名H∗的点,事实上x,y∈H∗=G-N∗(w),根据命名规则可知,x=(x1,x2,···,xr)和y=(y1,y2,···,yr)是彼此不邻接的,故G中任意两点都彼此不邻接,所以(n1+1,n2+1,···nr+1),再由点的邻接关系HPK(n1+1,n2+1,···nr+1)是唯一最小的r-1维超平面完备残差图.
4 任意维超平面完备残差图的一个重要的性质
这一节主要是讨论任意维超平面完备残差图的结构,主要有下面的结果.
定理4.1若G是HPK(n1,n2,···,nr)-残差图,n1,n2,···,nr≥r+2 ≥ 5,则有ν(G)=k(n1+1)(n2+1)···(nr+1),G=G1+G2+···+Gk,且GiHPK(n1+1,n2+1,···,nr+1),i=1,2,···,k.
为了证明此定理,先定义有关超平面的点独立集的坐标变换.
定义4.1如果H=HPK(n1,n2,···,nr),V(H)={ (x1,x2,···,xr)| 1≤xi≤ni,i=1,2,···,r},假设独立集S1={v1,v2,···,vr,v0} 与S2={u1,u2,···,ur,u0},且S1与S2都是(r+1)-独立集.S2与S1坐标变换定义如下,如果ui=vi,i=0,1,2,···,r;i/k,l,其中使得或者或者xj,或者或者yj,j=1,2,···,r,xj,yj/,i=0,1,2,···,r,则有
由定义4.1,可以直接得到下面引理.
引理4.1如果H=HPK(n1,n2,···,nr),V(H)={ (x1,x2,···,xr)| 1≤xi≤ni,i=1,2,···,r},n1,n2,···nr≥r+1 ≥ 4,则对任意u∈H,存在一个 (r+1)- 独立集{u1,u2,···,ur,u},可以和任何一个 (r+1)-独立集 {v1,v2,···,vr,v}进行坐标变换.
下面证明定理4.1.
设v0,v1,···,vr是图G中的r+1 独立集. 若Hi=G-N∗(vi)(n1,n2,···,nr),i=0,1,···,r. 设G1=<H0∪H1∪H2∪···∪Hr>,假设G1⊂G是G中由H0,H1,···,Hr生成的最小子图,显然,vi/∈Hi,以及vi∈Hj,i,j=0,1,2.N∗(vi)∩V(Hi)=φ,i=0,1,2,···,r,因此有

下证G1(n1+1,n2+1,···,nr+1),因为G1-N∗(vi)=HiHPK(n1,n2,···,nr),则有

以及
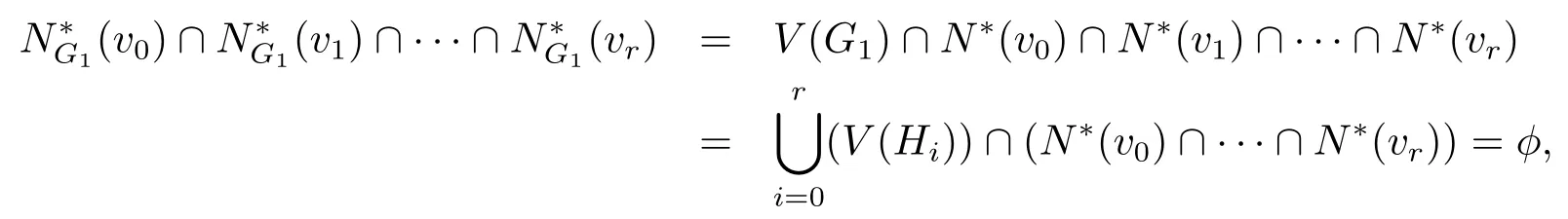
再由引理3.4和引理3.5可知.

如果G1=G,再根据定理3.2知,G是最小阶的HPK(n1,n2,···,nr)-残差图.如果G1/G,设N∗(v0)∩N∗(v1)∩ ···∩N∗(vr)=W,则有以及G1=G-W,并且V(G1)∩W=,因此V(G1)⊆V(G)-W.对于任意x∈V(G)-W,有,以及(vi),对任意的i,有x∈G-N∗(vi)=Hi⊂G1,所以V(G)-W⊆V(G1),以及G1=G-W,故有G1是HPK(n1,n2,···,nr)-残差图.
由上面证明可知任意的x∈G1都与任意w∈W邻接.下面证明对于任意的x∈H0,x都与任意的w∈W邻接的.因为H0=G-N∗(v0),所以有{v1,v2,···,vr}⊂V(H0),由条件可知v∈H0以及{v1,v2,···,vr,v}是H0的(r+1)-独立集,且v也是与任意的w∈W邻接的,若不然,v不与w∗∈W邻接,则有以及{v0,v1,···,vr}⊂V(H)是H(r+1)-独立集,因此存在w∗∈H,即,这与引理3.2矛盾,故有W⊂N∗(v).

因为n1,n2,···,nr≥r+2 ≥ 5,因此存在两点u,v∈H0,使得 {v1,v2,···,vr,u,v}⊂V(H)是(r+2)-独立集,则W⊂N∗(u)∩N∗(v).现在假设是(r+2)-独立集,则H0中存在另一点{v1,v2,···,vr,u,v}与之进行坐标变换.根据上面的讨论同样可得,再由引理3.1可知对任意x∈H0,以及x∈G1,都有x是与任意w∈W邻接的,因此有

下面证明G1是HPK(n1,n2,···,nr)-残差图.由于ν(G)=(n1+1)(n2+1)···(nr+1),根据定理3.2,有(n1+1,n2+1,···,nr+1).又因为任意w∈W,则有V(G1)⊂N∗(w).设<W>=F,则有G=G1+F以及

由于w∈W的任意性,F是HPK(n1,n2,···,nr)-残差图,所以对F可以类似的讨论,G2的一个最小子图,则G2(n1+1,n2+1,···,nr+1),F=G2+F1,其中F1=F-V(G2).重复前面在G中的讨论,则有

5 多重超平面完备残差图的最小阶和唯一极图
根据多重超平面残差图的定义容易得到引理5.1和5.2.
引理5.1若G=(V,E),{v0,v1,···,vr}∈G⊂V(G)是G中(k+1)-独立集,则有

其中F=G-N∗(v0).
引理5.2令G=(V,E),u1,u2,···,uk∈G,{v0,v1,···,vr}⊂V(G)是G中 (r+1)-独立集,对每一个vi都不与uj邻接.令Fi=G-N∗(vi),i=1,2,···,l,则有

由任意维超平面残差图的性质也可以得到m重任意维超平面残差图的性质.
引理5.3若G是HPK(n1,n2,···,nr)-残差图,H=HPK(n1+1,n2+1,···,nr+1),n1,n2,···,nr≥r≥ 3. 令 {v1,v2,···,vk}⊂V(G)以及 {u1,u2,···,uk}⊂V(H)分别是G和H中的k-独立集,则有
证当k≥r+1,由引理3.3可知

则上面不等式成立.下面假设1≤k≤r,则存在v∈G和u∈H,且有{v1,v2,···,vk,v}{u1,u2,···,uk,u}分别是G和H中(k+1)-独立集.设G1=G-N∗(v),H1=H-N∗(u),则有G1H1(n1,n2,···,nr),{v1,v2,···,vk}⊂V(G1) 以及 {u1,u2,···,uk}⊂V(H1)分别是G1和H1的k-独立集,且有
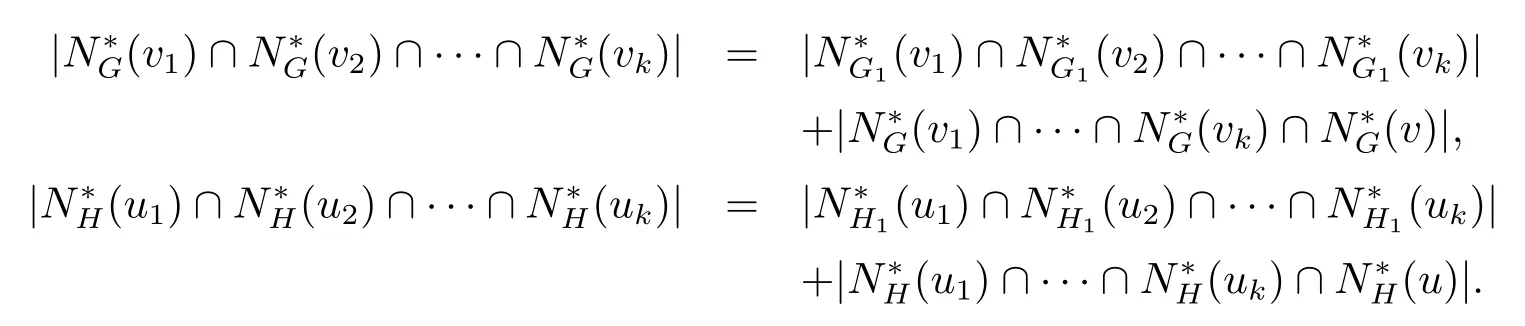
因为G11(n1,n2,···,nr),由引理 3.4 知

由此可知当k≥r+1,k=r,r-1,···,3,2,1.上面不定式成立的.
引理5.4假设G是 2-HPK(n1,n2,···,nr)-残差图,H=HPK(n1+2,n2+2,···,nr+2),n1,n2,···,nr≥r≥ 3{v1,v2,···,vk}⊂V(G) 和 {u1,u2,···,uk}⊂V(H)分别是G和H的k-独立集,则有

证由引理3.3知,k≥r+1不等式是显然成立的,下面假设1≤k≤r,根据引理5.3的讨论,在G和H中存在点v∈G,u∈H,使得G1=G-N∗(v),H1=H-N∗(u),以及 {v1,v2,···,vk}⊂V(G1)和 {u1,u2,···,uk}⊂V(H1). 因为G1是HPK(n1,n2,···,nr)-残差图,以及H1=HPK(n1+1,n2+1,···,nr+1),因此当k≥r+1不等式成立,k=r,r-1,···,3,2,1.
引理5.5假设G是m-HPK(n1,n2,···,nr)-残差图,H=HPK(n1+m,n2+m,···,nr+m),n1,n2,···,nr≥r≥ 3,{v1,v2,···,vr}⊂V(G) 和 {u1,u2,···,uk}⊂V(H)分别是G和H的k-独立集,则有
证当m=1,2,有引理5.3和引理5.4知成立的.下面对m用数学归纳法证明,假设对m-1成立,由引理3.3可知k≥r+1时,不等式成立,讨论与引理5.3,5.4的讨论一样可以得到,对于m,k≥r+1,k=r,r-1,···,3,2,1是成立的.
定理5.1假设G是m-HPK(n1,n2,···,nr)-残差图,n1,n2,···,nr≥r≥3,则有ν(G)≥ (n1+m)(n2+m)···(nr+m).
证当m=1,由定理3.1可知,结论成立.利用数学归纳法,假设当m-1≥1成立,当为m时,G是m-HPK(n1,n2,···,nr)-残差图,H=HPK(n1+m,n2+m,···,nr+m).由引理5.4知,,对于G和H中的任意一点v∈G,u∈H.设G1=G-N∗(v),H1=H-N∗(u),则有G1是 (m-1)-HPK(n1,n2,···,nr)-残差图,故有

利用归纳假设有

定理5.2假设G是m-HPK(n1,n2,···,nr)-残差图,n1,n2,···,nr≥r≥3,以及ν(G)=(n1+m)(n2+m)···(nr+m),则有GHPK(n1+m,n2+m,···,nr+m).
证设G是m-HPK(n1,n2,···,nr)-残差图,H=HPK(n1+m,n2+m,···,nr+m),n1,n2,···,nr≥r≥3,ν(G)=ν(H).当m=1 时,由定理 3.2 可知,(n1+1,n2+1,···,nr+1).利用数学归纳法,假设m-1≥1成立.对于m,存在点v∈G和u∈H,有G1=G-N∗(v)是 (m-1)-HPK(n1,n2,···,nr)-残差图,以及H1=H-N∗(u)=HPK(n1+m-1,···,nr+m-1).再由引理5.5 定理 5.1,有
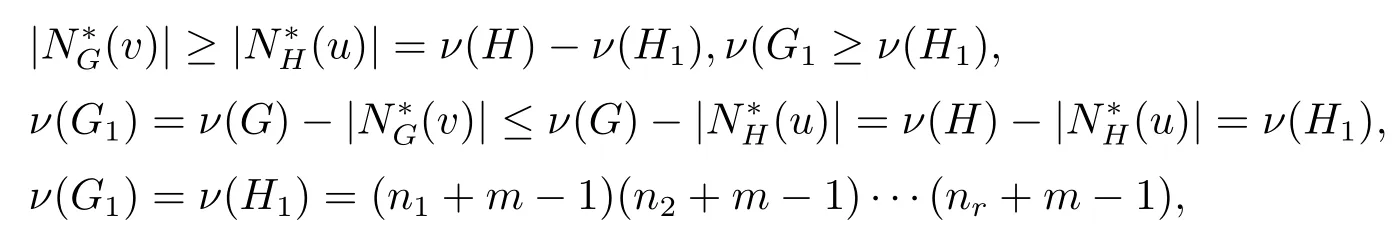
因此有G1是最小阶的(m-1)-HPK(n1,n2,···,nr)-残差图.根据归纳假设有G1(n1+m-1,n2+m-1,···,nr+m-1).由于v是G中任意一点,根据定义2.2知,G是最小阶的HPK(n1+m-1,n2+m-1,···,nr+m-1)-残差图,设=ni+m-1≥ni≥r≥ 3,i=1,2,···,r,由定理 3.2 可知(n1+m,n2+m,···,nr+m). 证毕.
[2]杨世辉,段辉明.奇阶完备残差图[J].应用数学学报,2011,34(5):778-785.
[3]Liao J,Yang S,Deng Y.On connected 2-Kn-residual graphs[J].Mediterranean J.Math.,2012,6:12-27.
[4]段辉明,曾波,窦智.连通的三重Kn-残差图[J].运筹学学报,2014,18:59-68.
[5]Liao J,Long G,Li M.Erds conjecture on connected residual graphs[J].J.Comput.,2012,7:1497-1502.
[7]Trotta B.Residual properties of simple graphs[J].Bull.Austr.Math.Soc.,2010,82:488-504.
[8]段辉明,曾波,李永红.关于m-HPK(n1,n2,n3,n4)-残差图[J].数学杂志,2014,34(2):324-334.
[9]Duan H.On connectedmmultiply 2 dimensions composite hyperplanne complete graph’s residual graphs[J].J.Discrete Math.Sci.Crytography,2014,16:313-328.
[10]Yang H S.The isomorphic factorization of complete tripartite graphsK(m,n,s)-a proof of F.Harary,R.W.Robinson and N.C.Wormald’s conjecture[J].Disc.Math.,1995,145(1-3):239-257.
[11]Liang Z,Zuo H.On the gracefulness of the graph[J].Appl.Anal.Discrete Math.,2010,10:175-180.
MULTIPLY HYPERPLANE COMPLETE RESIDUAL GRAPH
DUAN Hui-ming1,SHAO Kai-liang1,ZHANG Qing-hua1,ZENG Bo2
(1.College of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)(2.School of Business Planning,Chongqing Technology and Business University,Chongqing 400067,China)
In this paper,we study any number of dimensions hyperplane complete residual graphs and multiply any number of dimensions hyperplane complete residual graphs,and extend Erds,Harary and Klawe’s de fi nition of plane complete residual graph to hyperplane and obtain dimensions hyperplane complete residual graph.With the method of including excluding principle and set operation,we obtain the minimum order of any number of dimensions hyperplane complete residual graphs and a unique minimal any number of dimensions hyperplane complete residual graph,and an important property of any number of dimensions hyperplane complete residual graph.In addition,we obtain the minimum order of multiply any number of dimensions hyperplane complete residual graphs and a unique minimal multiply any number of dimensions hyperplane complete-residual graphs.
residually graph;close neighborhood;isomorphic;independent set
on:05C35;05C60;05C75
O157.5
A
0255-7797(2017)04-0833-12
2015-08-24接收日期:2015-12-21
国家自然科学基金(11671001;61472056);重庆自然科学基金(cstc2015jcyjA00034;cstc2015jcyjA00015);重庆市教育委员会科学技术研究(KJ1600425;KJ1500403).
段辉明(1976-),女,重庆铜梁,讲师,主要研究方向:组合数学.
- 数学杂志的其它文章
- k-NORMAL DISTRIBUTION AND ITS APPLICATIONS
- ROSSBY WAVES WITH THE CHANGE OFβAND THE INFLUENCE OF TOPOGRAPHY IN A TWO-LAYER FLUID
- ASYMPTOTIC PROPERTIES OF A CLASS OF NONLINEAR STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY
- TOTALLY UMBILICAL SUBMANIFOLD ON RIEMANNIAN MANIFOLD WITH AN ORTHOGONAL CONNECTION
- ON A SINGULAR ELLIPTIC SYSTEM INVOLVING THE CAFFARELLI-KOHN-NIRENBERG INEQUALITY
- 关于square-full数上的函数的均值估计

